
4 Estadística descriptiva
Cuando se dispone de un nuevo conjunto de datos, una de las primeras tareas que hay que hacer es encontrar la manera de resumirlos de forma compacta y fácil de entender. En eso consiste la estadística descriptiva (a diferencia de la estadística inferencial). De hecho, para mucha gente el término “estadística” es sinónimo de estadística descriptiva. Este es el tema que trataremos en este capítulo, pero antes de entrar en detalles, tomemos un momento para entender por qué necesitamos la estadística descriptiva. Para ello, abramos el archivo aflsmall_margins y veamos qué variables están almacenadas en él, véase Figure 4.1.
De hecho, aquí solo hay una variable, afl.margins. Nos centraremos un poco en esta variable en este capítulo, así que será mejor que te diga lo que es. A diferencia de la mayoría de los conjuntos de datos de este libro, se trata en realidad de datos reales relativos a la Liga de fútbol australiana (AFL).1 La variable afl.margins contiene el margen ganador (número de puntos) de los 176 partidos jugados en casa y fuera de casa durante la temporada 2010.
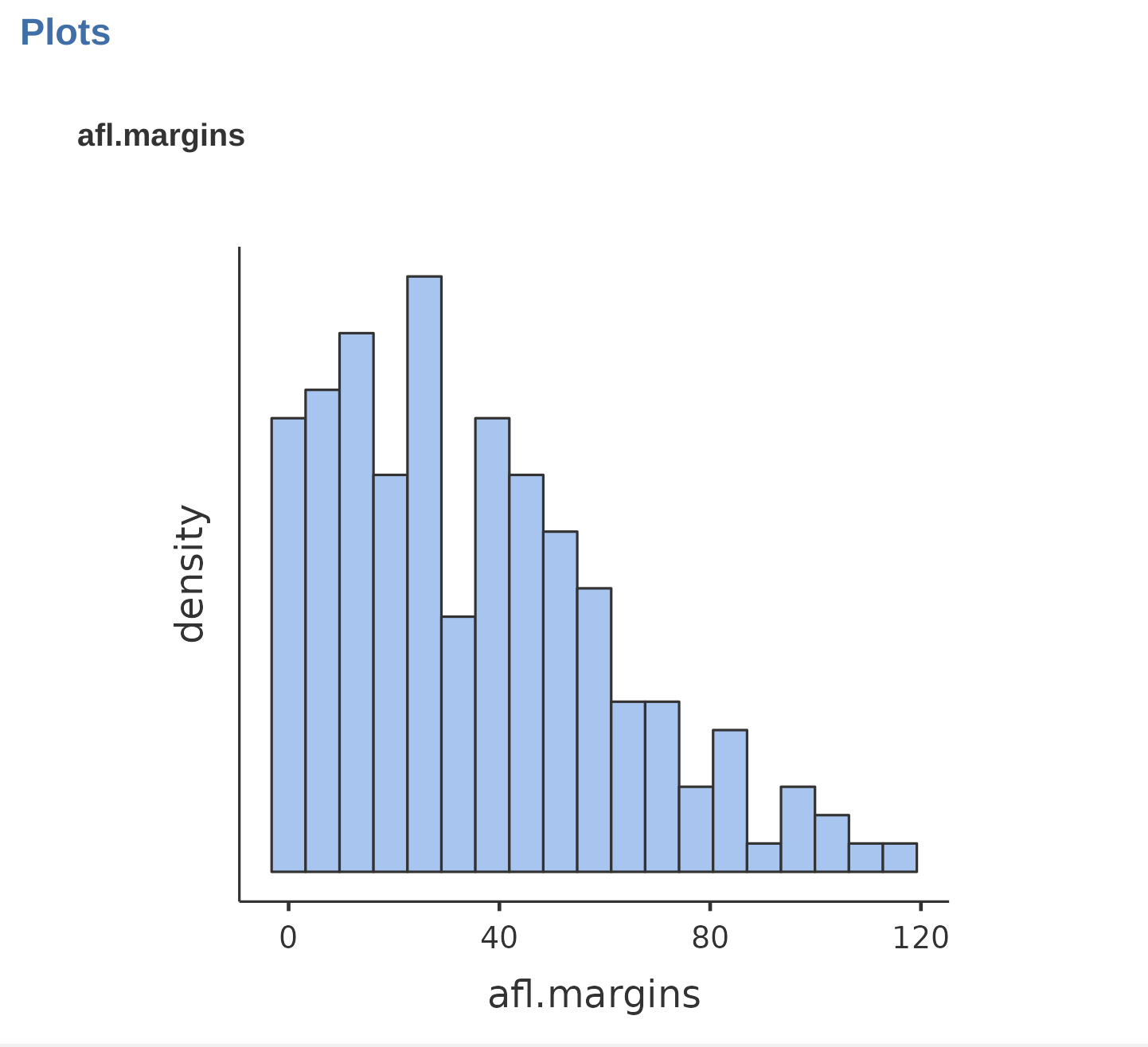
Este resultado no facilita la comprensión de lo que dicen realmente los datos. Simplemente “mirar los datos” no es una forma muy eficaz de entenderlos. Para hacernos una idea de lo que dicen realmente los datos, tenemos que calcular algunos estadísticos descriptivos (este capítulo) y dibujar algunas imágenes bonitas (Chapter 5). Dado que los estadísticos descriptivos son los más fáciles de los dos temas, comenzaremos con ellos, pero sin embargo, vamos a mostrar un histograma de los datos de afl.margins, ya que debería ayudar a tener una idea de cómo son los datos que estamos tratando de describir, ver Figure 4.2. Hablaremos mucho más sobre cómo dibujar histogramas en Section 5.1 en el próximo capítulo. Por ahora, basta con mirar el histograma y observar que proporciona una representación bastante interpretable de los datos de afl.margins.
4.1 Medidas de tendencia central
Dibujar los datos, como en Figure 4.2, es una excelente manera de transmitir la “esencia” de lo que los datos intentan decirnos. Suele ser muy útil tratar de condensar los datos en unos cuantos estadísticos “resumidos” sencillos. En la mayoría de las situaciones, lo primero que querrás calcular es una medida de tendencia central. Es decir, te gustaría saber dónde se encuentra el “promedio” o el “medio” de tus datos. Las tres medidas más utilizadas son la media, la mediana y la moda. Explicaremos cada una de ellas, y luego discutiremos cuándo es útil cada una de ellas.
4.1.1 La media
La media de un conjunto de observaciones no es más que un promedio normal y corriente. Se suman todos los valores y se dividen por el número total de valores. Los cinco primeros márgenes ganadores de la AFL fueron 56, 31, 56, 8 y 32, por lo que la media de estas observaciones es simplemente:
\[ \frac{56 + 31 + 56 + 8 + 32}{5} = \frac{183}{5} = 36,60 \] Por supuesto, esta definición de la media no es nueva para nadie. Los promedios (es decir, las medias) se usan tan a menudo en la vida cotidiana que se trata de algo bastante familiar. Sin embargo, dado que el concepto de media es algo que todo el mundo entiende, usaré esto como excusa para empezar a introducir algo de la notación matemática que los estadísticos utilizan para describir este cálculo y hablar de cómo se harían los cálculos en jamovi.
La primera notación que hay que introducir es \(N\), que usaremos para referirnos al número de observaciones que estamos promediando (en este caso, \(N = 5\)). A continuación, debemos adjuntar una etiqueta a las observaciones. Es habitual usar X para esto y utilizar subíndices para indicar de qué observación estamos hablando. Es decir, usaremos \(X_1\) para referirnos a la primera observación, \(X_2\) para referirnos a la segunda observación, y así sucesivamente hasta llegar a \(X_N\) para la última. O, para decir lo mismo de una manera un poco más abstracta, usamos \(X_i\) para referirnos a la i-ésima observación. Solo para asegurarnos de que tenemos clara la notación, Table 4.1 enumera las 5 observaciones en la variable afl.margins, junto con el símbolo matemático utilizado para referirse a ella y el valor real al que corresponde la observación.
| the observation | its symbol | the observed value |
|---|---|---|
| winning margin, game 1 | \( X_1 \) | 56 points |
| winning margin, game 2 | \( X_2 \) | 31 points |
| winning margin, game 3 | \( X_3 \) | 56 points |
| winning margin, game 4 | \( X_4 \) | 8 points |
| winning margin, game 5 | \( X_5 \) | 32 points |
[Detalle técnico adicional2]
4.1.2 Cálculo de la media en jamovi
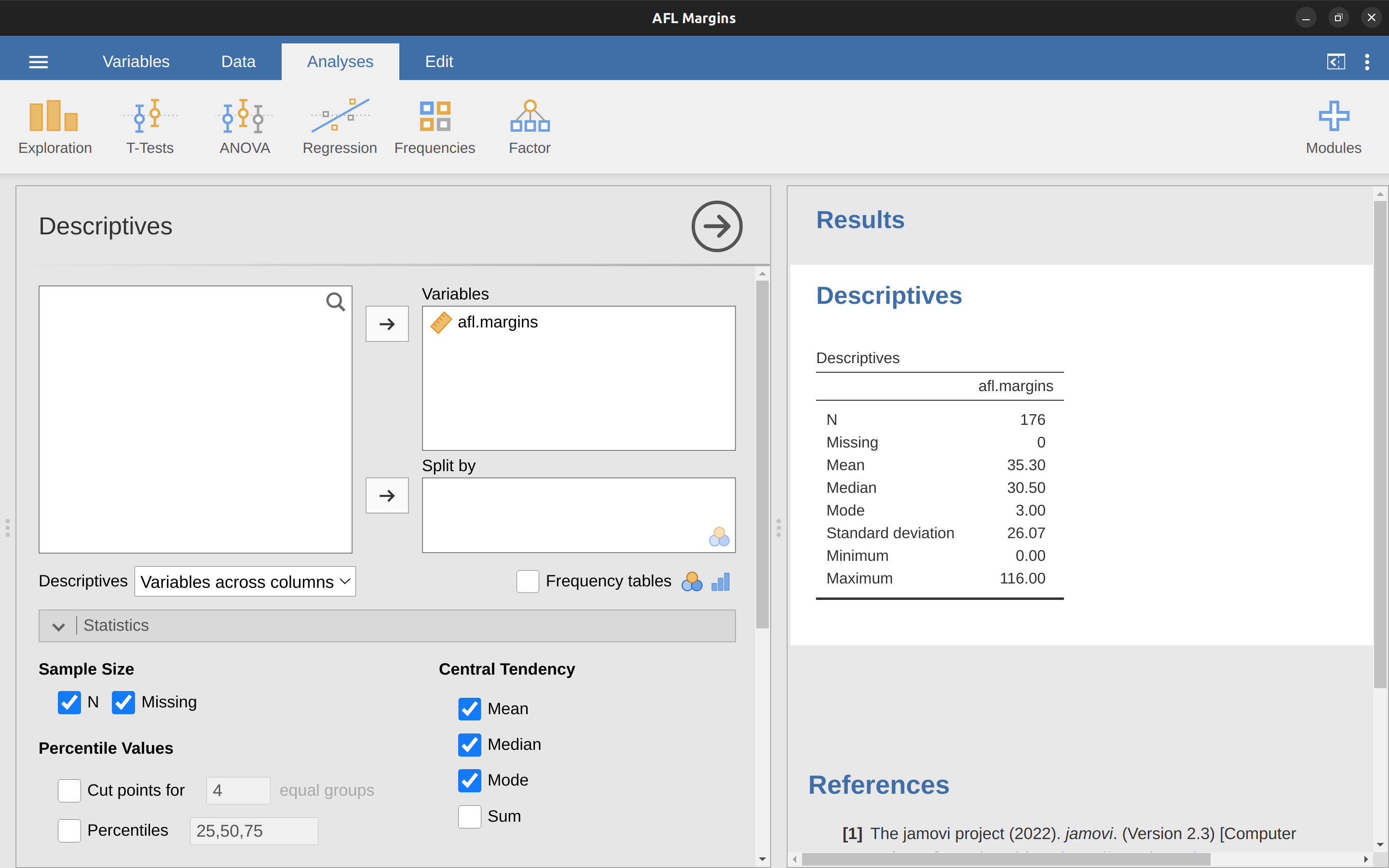
Bien, esas son las matemáticas. Entonces, ¿cómo conseguimos que la caja mágica de la informática haga el trabajo por nosotros? Cuando el número de observaciones comienza a ser grande, es mucho más fácil hacer este tipo de cálculos con un ordenador. Para calcular la media usando todos los datos podemos utilizar jamovi. El primer paso es hacer clic en el botón ‘Exploración’ y luego hacer clic en ‘Descriptivos’. A continuación, marca la variable afl.margins y haz clic en la flecha hacia la derecha para moverla al cuadro ‘Variables’. En cuanto lo hagas, aparecerá una tabla en la parte derecha de la pantalla con información por defecto sobre los ‘Descriptivos’; ver Figure 4.3.
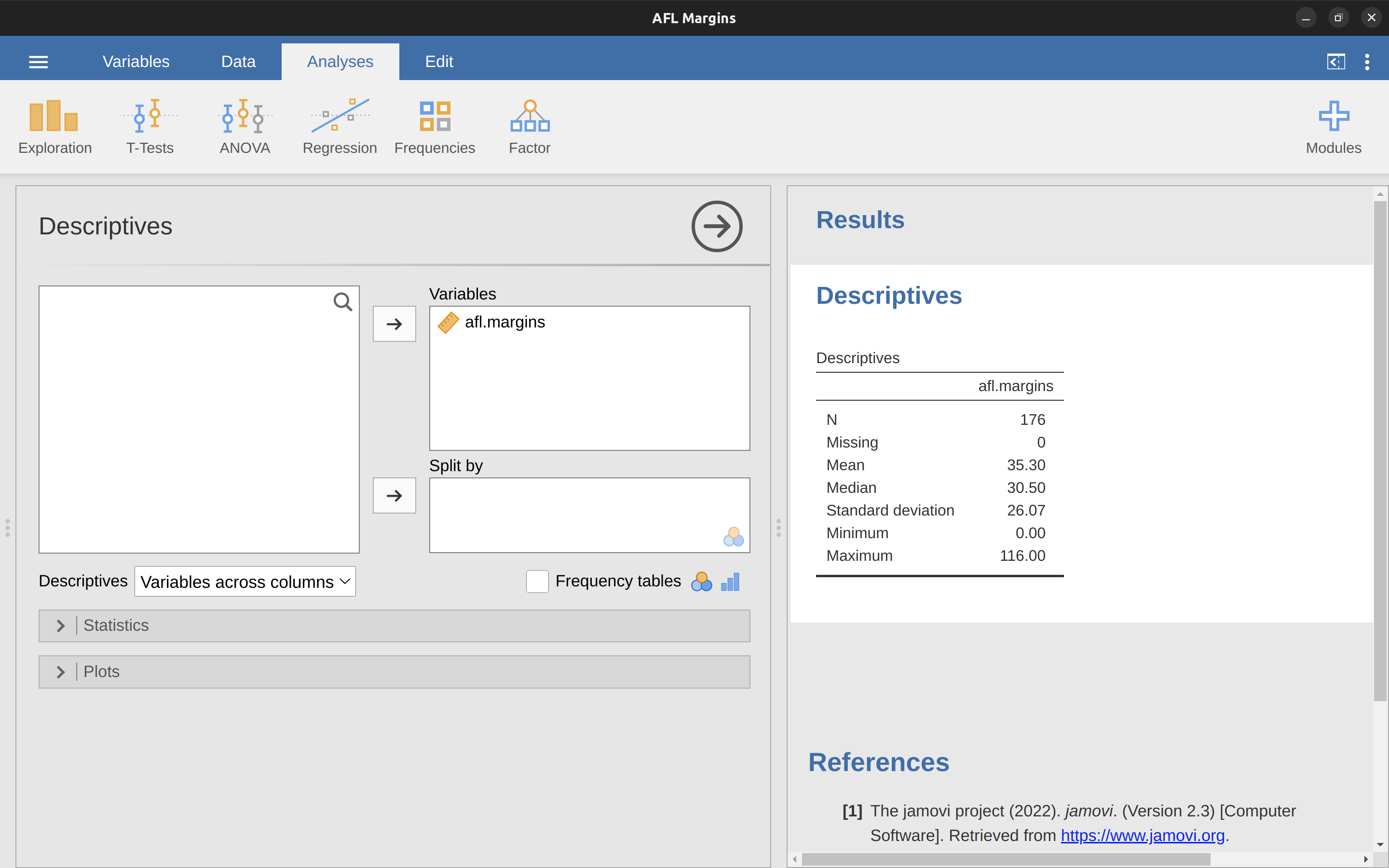
Como puedes ver en Figure 4.3, el valor medio de la variable afl.margins es 35,30. Otra información presentada incluye el número total de observaciones (N=176), el número de valores perdidos (ninguno) y los valores de la mediana, mínimo y máximo de la variable.
4.1.3 La mediana
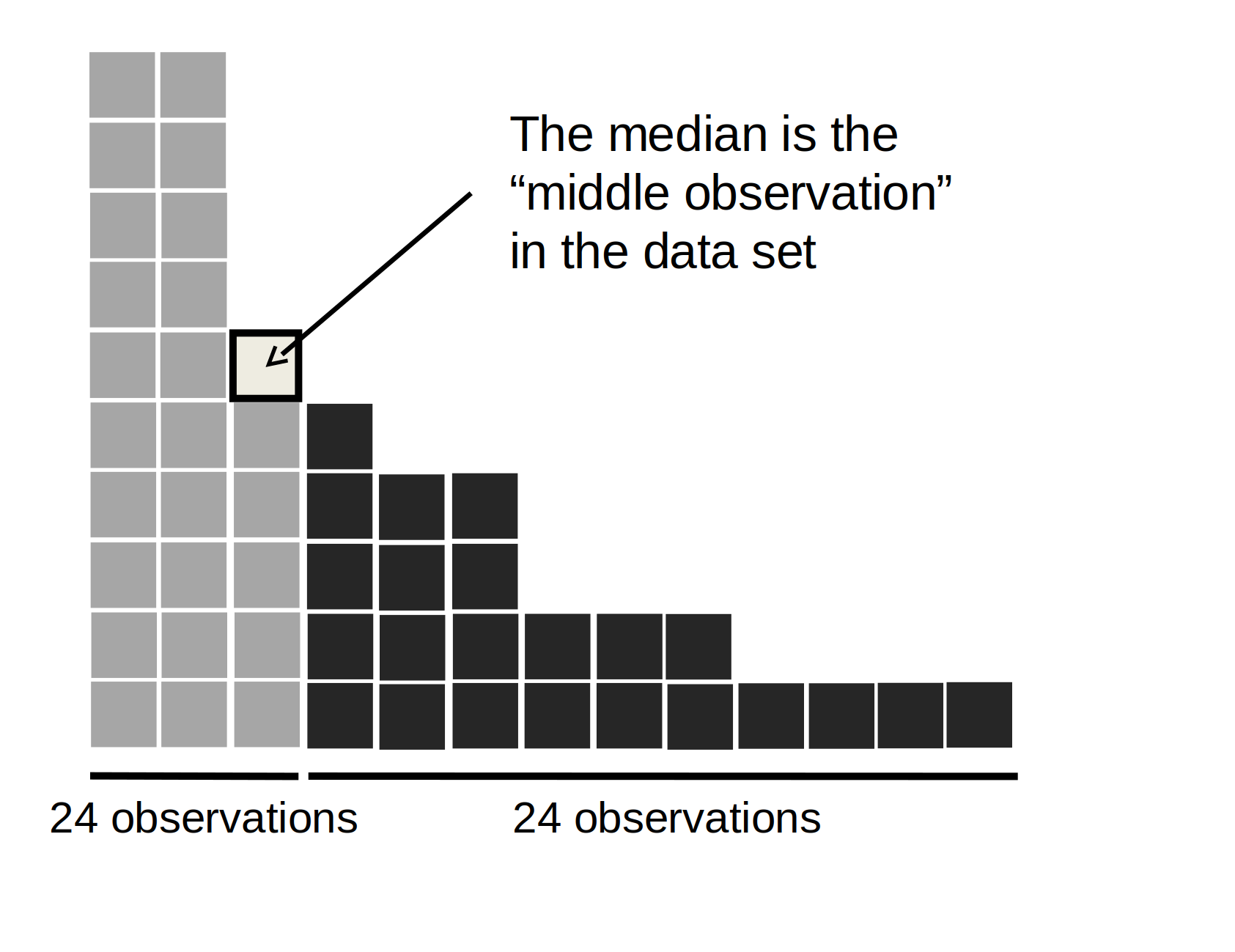
La segunda medida de tendencia central que la gente usa mucho es la mediana, y es incluso más fácil de describir que la media. La mediana de un conjunto de observaciones es simplemente el valor medio. Como antes, imaginemos que solo nos interesan los primeros 5 márgenes ganadores de la AFL: \(56\), \(31\), \(56\), \(8\) y \(32\). Para calcular la mediana ordenamos estos números en orden ascendente:
8, 31, 32, 56, 56
A partir de la inspección, es obvio que el valor mediano de estas 5 observaciones es 32, ya que es el del medio en la lista ordenada (lo he puesto en negrita para que sea aún más obvio). Esto es fácil. Pero, ¿qué debemos hacer si nos interesan los primeros 6 partidos en lugar de los primeros 5? Como el sexto partido de la temporada tuvo un margen de ganancia de 14 puntos, nuestra lista ordenada ahora es
8, 14, 31, 32, 56, 56
y hay dos números en el medio, 31 y 32. La mediana se define como el promedio de esos dos números, que por supuesto es 31,5. Como antes, es muy tedioso hacer esto a mano cuando se tienen muchos números. En la vida real, por supuesto, nadie calcula la mediana ordenando los datos y buscando el valor medio. En la vida real usamos un ordenador para que haga el trabajo pesado por nosotras, y jamovi nos ha proporcionado un valor de mediana de 30.50 para la variable afl.margins (Figure 4.3).
4.1.4 ¿Media o mediana? ¿Cuál es la diferencia?
Saber calcular medias y medianas es solo una parte de la historia. También hay que entender qué dice cada una de ellas sobre los datos y lo que eso implica en relación a cuándo se debe usar cada una. Esto se ilustra en Figure 4.4. La media es algo así como el “centro de gravedad” del conjunto de datos, mientras que la mediana es el “valor medio” de los datos. Lo que esto implica, en cuanto a cuál deberías usar, depende un poco del tipo de datos que tengas y de lo que estés intentando conseguir. Como guía aproximada:
- Si tus datos son de escala nominal, probablemente no deberías usar ni la media ni la mediana. Tanto la media como la mediana se basan en la idea de que los números asignados a los valores son significativos. Si el esquema de numeración es arbitrario, probablemente sea mejor usar la Moda en su lugar.
- Si tus datos son de escala ordinal, es más probable que quieras usar la mediana que la media. La mediana solo utiliza la información de orden de los datos (es decir, qué números son mayores) pero no depende de los números exactos involucrados. Esta es exactamente la situación que se da cuando tus datos son de escala ordinal. La media, por otro lado, utiliza los valores numéricos precisos asignados a las observaciones, por lo que no es realmente apropiada para datos ordinales.
- Para datos de escala de intervalo y razón, cualquiera de los dos suele ser aceptable. La elección depende un poco de lo que se quiera conseguir. La media tiene la ventaja de que utiliza toda la información de los datos (lo cual es útil cuando no se dispone de muchos datos). Pero es muy sensible a los valores extremos y atípicos.
Vamos a ampliar un poco esta última parte. Una consecuencia es que hay diferencias sistemáticas entre la media y la mediana cuando el histograma es asimétrico (asimetría y apuntamiento). Esto se ilustra en Figure 4.4. Observa que la mediana (a la derecha) se sitúa más cerca del “cuerpo” del histograma, mientras que la media (a la izquierda) se arrastra hacia la “cola” (donde están los valores extremos). Por poner un ejemplo concreto, supongamos que Bob (ingreso $50 000), Kate (ingreso $60 000) y Jane (ingreso $65 000) están sentados en una mesa. La renta media de la mesa es $58,333 y la renta mediana es $60,000. Entonces Bill se sienta con ellos (ingresos $100,000,000). La renta media ha subido a $25,043,750 pero la mediana sube solo a $62,500. Si lo que te interesa es ver la renta total en la tabla, la media podría ser la respuesta correcta. Pero si lo que te interesa es lo que se considera una renta típica en la mesa, la mediana sería una mejor opción.

4.1.5 Un ejemplo de la vida real
Para intentar entender por qué hay que prestar atención a las diferencias entre la media y la mediana, veamos un ejemplo de la vida real. Como suelo burlarme de los periodistas por sus escasos conocimientos científicos y estadísticos, debo dar crédito a quienes lo merecen. Este es un excelente artículo de la web de noticias ABC3 del 24 de septiembre de 2010:
En las últimas semanas ejecutivos sénior del Commonwealth Bank han viajado por todo el mundo con una presentación en la que muestran cómo los precios de la vivienda en Australia y las principales relaciones precio-renta clave se comparan favorablemente con países similares. “La asequibilidad de la vivienda en realidad ha ido a la baja en los últimos cinco o seis años”, afirmó Craig James, economista jefe de CommSec, la división de negociación del banco.
Esto probablemente sea una gran sorpresa para cualquiera que tenga una hipoteca, o que quiera una hipoteca, o que pague el alquiler, o que no sea completamente ajeno a lo que ha estado ocurriendo en el mercado inmobiliario australiano en los últimos años. De vuelta al artículo:
CBA ha declarado la guerra a los que considera agoreros de la vivienda con gráficos, cifras y comparaciones internacionales. En su presentación, el banco rechaza los argumentos de que la vivienda en Australia es relativamente cara en comparación con los ingresos. Afirma que la relación entre el precio de la vivienda y la renta familiar en Australia, de 5,6 en las principales ciudades y de 4,3 en todo el país, es comparable a la de muchos otros países desarrollados. Dice que San Francisco y Nueva York tienen una relación de 7, Auckland es 6.7 y Vancouver de 9.3.
¡Más excelentes noticias! Excepto que el artículo continúa haciendo la observación de que:
Muchos analistas afirman que eso ha llevado al banco a utilizar cifras y comparaciones engañosas. Si se va a la página cuatro de la presentación del CBA y se lee la información de la fuente en la parte inferior del gráfico y la tabla, se observará que hay una fuente adicional en la comparación internacional: Demographia. Sin embargo, si el Commonwealth Bank también hubiera utilizado el análisis de Demographia en la relación entre el precio de la vivienda y la renta en Australia, habría obtenido una cifra más cercana a 9 en lugar de 5,6 o 4,3.
Se trata de una discrepancia bastante seria. Un grupo de personas dice 9, otro dice 4-5. ¿Deberíamos dividir la diferencia y decir que la verdad está en algún punto intermedio? Por supuesto que no. Esta es una situación en la que hay una respuesta correcta y otra incorrecta. Demographia tiene razón y el Commonwealth Bank está equivocado. Como señala el artículo:
[Un] problema obvio de las cifras de precios e ingresos del Commonwealth Bank es que comparan los ingresos medios con los precios medianos de la vivienda (a diferencia de las cifras de Demographia que comparan los ingresos medianos con los precios medianos). La mediana es el punto medio, reduciendo eficazmente los altibajos, y eso significa que el promedio es generalmente más alto cuando se trata de ingresos y precios de activos, porque incluye los ingresos de las personas más ricas de Australia. Dicho de otro modo: las cifras del Commonwealth Bank tienen en cuenta el sueldo multimillonario de Ralph Norris en lo que respecta a los ingresos, pero no su (sin duda) carísima casa en las cifras del precio de los bienes inmuebles, con lo que subestiman la relación entre el precio de la vivienda y los ingresos de los australianos con rentas medias.
Yo no lo habría expresado mejor. La forma en que Demographia calculó la proporción es la correcta. La forma en que lo hizo el Banco es incorrecta. En cuanto a por qué una organización tan sofisticada cuantitativamente como un gran banco cometió un error tan elemental, bueno… No puedo asegurarlo ya que no tengo ningún conocimiento especial de su forma de pensar. Pero el propio artículo menciona los siguientes hechos, que pueden o no ser relevantes:
[Como] el mayor prestamista hipotecario de Australia, el Commonwealth Bank, tiene uno de los mayores intereses creados en el aumento de los precios de la vivienda. Efectivamente, posee una gran cantidad de viviendas australianas como garantía de sus préstamos hipotecarios, así como de muchos préstamos a pequeñas empresas.
Vaya, vaya.
4.1.6 Moda
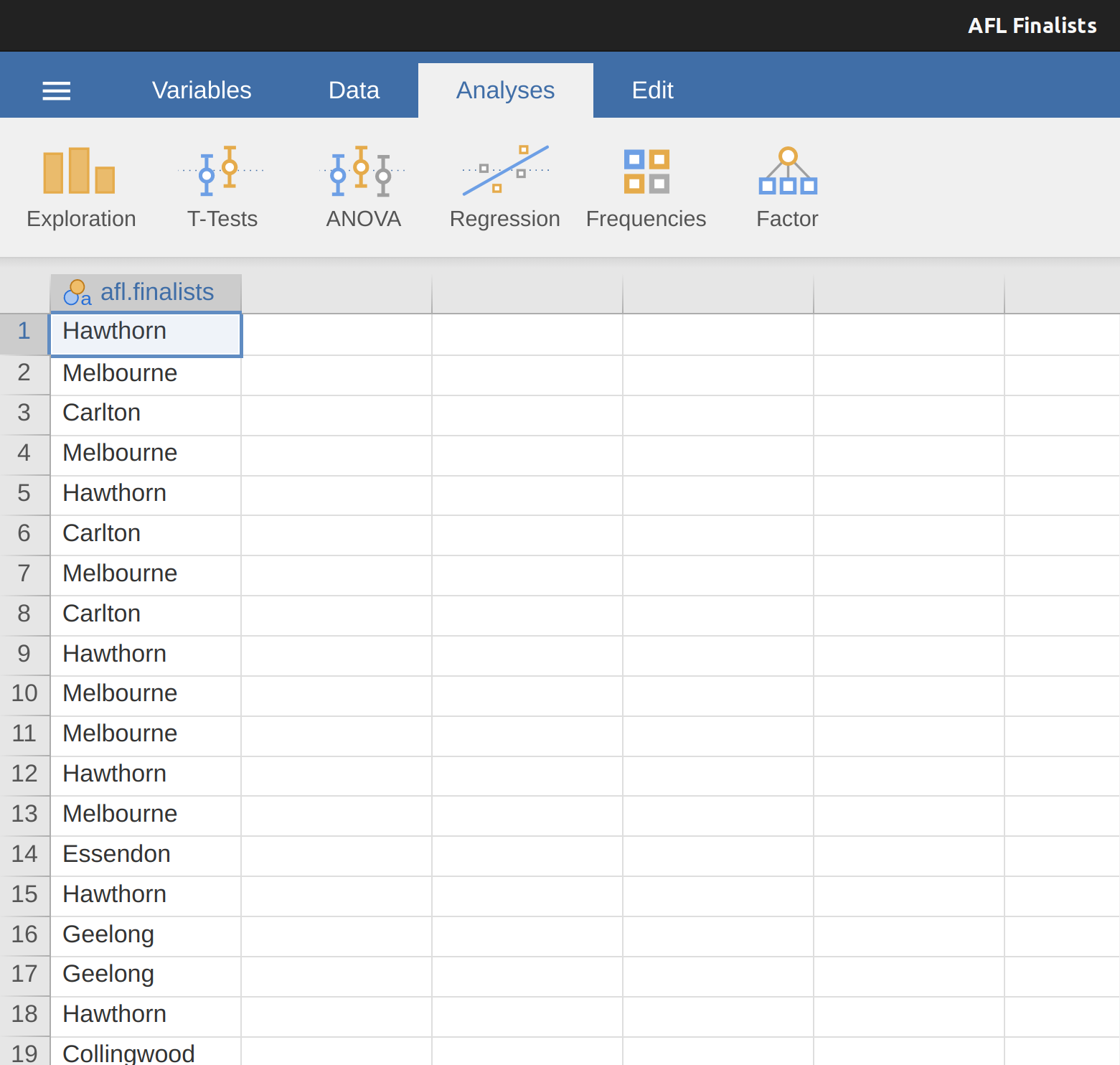
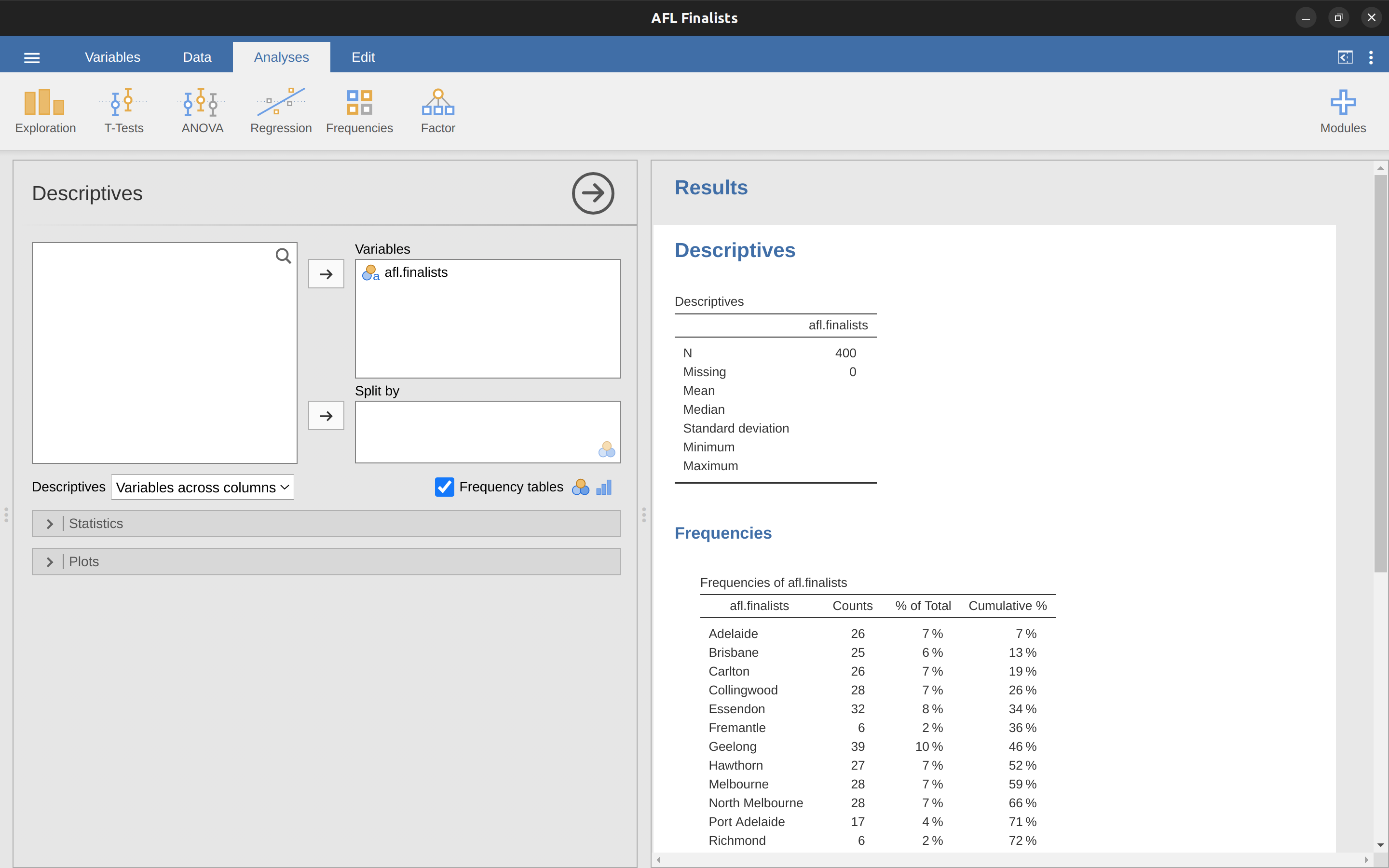
La moda de una muestra es muy sencilla. Es el valor que aparece con más frecuencia. Podemos ilustrar la moda utilizando una variable diferente de la AFL: ¿quién ha jugado más finales? Abre el archivo de finalistas de aflsmall y echa un vistazo a la variable afl.finalists, ver Figure 4.5. Esta variable contiene los nombres de los 400 equipos que jugaron en las 200 finales disputadas durante el período de 1987 a 2010.
Lo que podríamos hacer es leer las 400 entradas y contar el número de veces en las que aparece el nombre de cada equipo en nuestra lista de finalistas, produciendo así una tabla de frecuencias. Sin embargo, sería una tarea aburrida y sin sentido: exactamente el tipo de tarea para la que los ordenadores son excelentes. Así que usemos jamovi para que lo haga por nosotros. En ‘Exploración’ - ‘Descriptivos’, haz clic en la pequeña casilla de verificación etiquetada como ‘Tablas de frecuencias’ y obtendrás algo como Figure 4.6.
Ahora que tenemos nuestra tabla de frecuencias, podemos mirarla y ver que, en los 24 años de los que tenemos datos, Geelong ha jugado más finales que cualquier otro equipo. Por lo tanto, la moda de los datos de afl.finalists es “Geelong”. Podemos ver que Geelong (39 finales) jugó más finales que cualquier otro equipo durante el período 1987-2010. También vale la pena señalar que en la tabla ‘Descriptivos’ no se calculan los resultados de Media, Mediana, Mínimo o Máximo. Esto se debe a que la variable afl.finalists es una variable de texto nominal, por lo que no tiene sentido calcular estos valores.
Una última observación sobre la moda. Aunque la moda se calcula con mayor frecuencia cuando se tienen datos nominales, porque las medias y las medianas son inútiles para ese tipo de variables, hay algunas situaciones en las que realmente se desea conocer la moda de una variable de escala ordinal, de intervalo o de escala de razón. Por ejemplo, volvamos a nuestra variable afl.margins. Esta variable es claramente una escala de razón (si no te queda claro, puede que te ayude volver a leer la sección sobre Section 2.2), por lo que en la mayoría de las situaciones la media o la mediana es la medida de tendencia central que quieres. Pero considera esta situación: un amigo te ofrece una apuesta y elige un partido de fútbol al azar. Sin saber quién juega, debes adivinar el margen ganador exacto. Si aciertas, ganas $50. Si no aciertas, pierdes $1. No hay premios de consolación por “casi” acertar. Tienes que acertar exactamente el margen ganador exacto. Para esta apuesta, la media y la mediana no te sirven para nada. Debes apostar por la moda. Para calcular la moda de la variable afl.margins en jamovi, vuelve a ese conjunto de datos y en la pantalla ‘Exploración’ - ‘Descriptivos’ verás que puedes ampliar la sección marcada como ‘Estadísticas’. Haz clic en la casilla de verificación marcada como ‘Moda’ y verás el valor modal presentado en la tabla ‘Descriptivos’, como en Figure 4.7. Así, los datos de 2010 sugieren que deberías apostar por un margen de 3 puntos.
4.2 Medidas de variabilidad
Todos los estadísticos que hemos analizado hasta ahora se refieren a la tendencia central. Es decir, todos hablan de qué valores están “en el medio” o son “populares” en los datos. Sin embargo, la tendencia central no es el único tipo de resumen estadístico que queremos calcular. Lo segundo que realmente queremos es una medida de la variabilidad de los datos. Es decir, ¿cuán “dispersos” están los datos? ¿Cómo de “alejados” de la media o la mediana tienden a estar los valores observados? Por ahora, vamos a suponer que los datos son de escala de intervalo o de razón, y seguiremos utilizando los datos de afl.margins. Usaremos estos datos para discutir varias medidas diferentes de dispersión, cada una con diferentes puntos fuertes y débiles.
4.2.1 Rango
El rango de una variable es muy sencillo. Es el valor mayor menos el valor menor. Para los datos de márgenes ganadores de la AFL, el valor máximo es 116 y el valor mínimo es 0. Aunque el rango es la forma más sencilla de cuantificar la noción de “variabilidad”, es una de las peores. Recuerda de nuestra discusión sobre la media que queremos que nuestra medida de resumen sea robusta. Si el conjunto de datos tiene uno o dos valores extremadamente malos, nos gustaría que nuestros estadísticos no se vean excesivamente influidos por estos casos. Por ejemplo, en una variable que contenga valores atípicos muy extremos
-100, 2, 3, 4, 5, 6, 7, 8, 9, 10
está claro que el rango no es robusto. Esta variable tiene un rango de 110, pero si se eliminara el valor atípico, tendríamos un rango de solo 8.
4.2.2 Rango intercuartílico
El rango intercuartílico (RIC) es como el rango, pero en lugar de la diferencia entre el valor mayor y el menor se toma la diferencia entre el percentil 25 y el percentil 75. Si aún no sabes qué es un percentil, el percentil 10 de un conjunto de datos es el número x más pequeño tal que el 10 % de los datos es menor que x. De hecho, ya nos hemos topado con la idea. La mediana de un conjunto de datos es su percentil 50. En jamovi puedes especificar fácilmente los percentiles 25, 50 y 75 haciendo clic en la casilla de verificación ‘Cuartiles’ de la pantalla ‘Exploración’ - ‘Descriptivas’ - ‘Estadísticas’.
Y no es sorprendente que en Figure 4.8 el percentil 50 sea el mismo que el valor de la mediana. Y, observando que $50,50 - 12,75 = $37,75, podemos ver que el rango intercuartílico para los datos de los márgenes ganadores de la AFL de 2010 es 37,75. Si bien es obvio cómo interpretar el rango, es un poco menos obvio cómo interpretar el RIC. La forma más sencilla de pensar en ello es la siguiente: el rango intercuartílico es el rango que abarca la “mitad central” de los datos. Es decir, una cuarta parte de los datos cae por debajo del percentil 25 y una cuarta parte de los datos está por encima del percentil 75, por lo que la “mitad central” de los datos se encuentra entre ambos. Y el RIC es el rango cubierto por esa mitad central.

4.2.3 Desviación absoluta media
Las dos medidas que hemos visto hasta ahora, el rango y el rango intercuartílico, se basan en la idea de que podemos medir la dispersión de los datos observando los percentiles de los datos. Sin embargo, esta no es la única manera de abordar el problema. Un enfoque diferente consiste en seleccionar un punto de referencia significativo (generalmente la media o la mediana) y, a continuación, informar las desviaciones “típicas” con respecto a ese punto de referencia. ¿Qué entendemos por desviación “típica”? Por lo general, se trata del valor medio o mediano de estas desviaciones. En la práctica, esto da lugar a dos medidas diferentes: la “desviación absoluta media” (de la media) y la “desviación absoluta mediana” (de la mediana). Por lo que he leído, la medida basada en la mediana parece usarse en estadística y parece ser la mejor de las dos. Pero, para ser sincera, no creo haber visto que se utilice mucho en psicología. Sin embargo, la medida basada en la media sí aparece ocasionalmente en psicología. En esta sección hablaré de la primera, y volveré a hablar de la segunda más adelante.
Como el párrafo anterior puede sonar un poco abstracto, vamos a repasar la desviación absoluta media de la media un poco más despacio. Un aspecto útil de esta medida es que su nombre indica exactamente cómo calcularla. Pensemos en nuestros datos de márgenes de victorias en la AFL y, una vez más, comenzaremos imaginando que solo hay 5 partidos en total, con márgenes de victorias de 56, 31, 56, 8 y 32. Dado que nuestros cálculos se basan en un examen de la desviación de algún punto de referencia (en este caso la media), lo primero que debemos calcular es la media, \(\bar{X}\). Para estas cinco observaciones, nuestra media es \(\bar{X} = 36,6\). El siguiente paso es convertir cada una de nuestras observaciones \(X_i\) en una puntuación de desviación. Para ello, calculando la diferencia entre la observación \(X_i\) y la media \(\bar{X}\). Es decir, la puntuación de desviación se define como \(X_i - \bar{X}\). Para la primera observación de nuestra muestra, esto equivale a $56 - 36,6 = 19,4 $. Bien, eso es bastante sencillo. El siguiente paso en el proceso es convertir estas desviaciones en desviaciones absolutas, y lo hacemos mediante la conversión de cualquier valor negativo en positivo. Matemáticamente, denotaremos el valor absoluto de \(-3\) como \(\mid -3 \mid\), por lo que decimos que \(\mid -3 \mid = 3\). Usamos el valor absoluto aquí porque realmente no nos importa si el valor es mayor o menor que la media, solo nos interesa lo cerca que está de la media. Para ayudar a que este proceso sea lo más obvio posible, Table 4.2 muestra estos cálculos para las cinco observaciones.
| English | notation | value | deviation from mean | absolute deviation |
|---|---|---|---|---|
| notation: | \(i\) | \(X_i\) | \(X_i - \bar{X} \) | \( \mid X_i - \bar{X} \mid \) |
| 1 | 56 | 19.4 | 19.4 | |
| 2 | 31 | -5.6 | 5.6 | |
| 3 | 56 | 19.4 | 19.4 | |
| 4 | 8 | -28.6 | 28.6 | |
| 5 | 32 | -4.6 | 4.6 |
Ahora que hemos calculado la puntuación de la desviación absoluta para cada observación del conjunto de datos, todo lo que tenemos que hacer es calcular la media de estas puntuaciones. Vamos a hacerlo:
\[ \frac{19,4 + 5,6 + 19,4 + 28,6 + 4,6}{5} = 15,52 \]
Y hemos terminado. La desviación absoluta media de estas cinco puntuaciones es 15,52.
[Detalle técnico adicional4]
4.2.4 Variancia
Aunque la medida de la desviación absoluta media tiene su utilidad, no es la mejor medida de variabilidad que se puede utilizar. Desde una perspectiva puramente matemática, hay algunas razones sólidas para preferir las desviaciones al cuadrado en lugar de las desviaciones absolutas. Si lo hacemos obtenemos una medida llamada variancia, que tiene muchas propiedades estadísticas realmente buenas que voy a ignorar,5 y un defecto psicológico del que voy a hacer un gran problema en un momento. La variancia de un conjunto de datos \(X\) a veces se escribe como Var( \(X\) ), pero se denota más comúnmente como \(s^2\) (la razón de esto se aclarará en breve).
[Detalle técnico adicional6]
Ahora que ya tenemos la idea básica, veamos un ejemplo concreto. Una vez más, utilizaremos como datos los cinco primeros juegos de la AFL. Si seguimos el mismo planteamiento que la última vez, obtendremos la información que se muestra en Table 4.3.
| English | maths: | value | deviation from mean | absolute deviation |
|---|---|---|---|---|
| notation: | \(i\) | \(X_i\) | \(X_i - \bar{X} \) | \( ( X_i - \bar{X} )^2 \) |
| 1 | 56 | 19.4 | 376.36 | |
| 2 | 31 | -5.6 | 31.36 | |
| 3 | 56 | 19.4 | 376.36 | |
| 4 | 8 | -28.6 | 817.96 | |
| 5 | 32 | -4.6 | 21.16 |
Esa última columna contiene todas nuestras desviaciones al cuadrado, así que todo lo que tenemos que hacer es promediarlas. Si lo hacemos a mano, es decir, con una calculadora, obtenemos una variancia de \(324,64\). Emocionante, ¿verdad? Por el momento, vamos a ignorar la pregunta candente que probablemente todas estáis pensando (es decir, ¿qué diablos significa realmente una variancia de $ 324.64 $?) Y en su lugar hablemos un poco más sobre cómo hacer los cálculos en jamovi, porque esto revelará algo muy extraño. Inicia una nueva sesión de jamovi haciendo clic en el botón del menú principal (tres líneas horizontales en la esquina superior izquierda) y seleccionan ‘Nuevo’. Ahora escribe los cinco primeros valores del conjunto de datos de afl.margins en la columna A (\(56\), \(31\) , \(56\), \(8\), \(32\). Cambia el tipo de variable a ‘Continua’ y, en ‘Descriptivas’, haz clic en la casilla de verificación ‘Variancia’ y obtendrás los mismos valores de variancia que calculamos a mano (\(324,64\)). No, espera, obtienes una respuesta completamente diferente ($ 405.80 $) - mira Figure 4.9. Eso es muy raro. ¿Jamovi no funciona? ¿Es un error tipográfico? ¿Soy idiota?
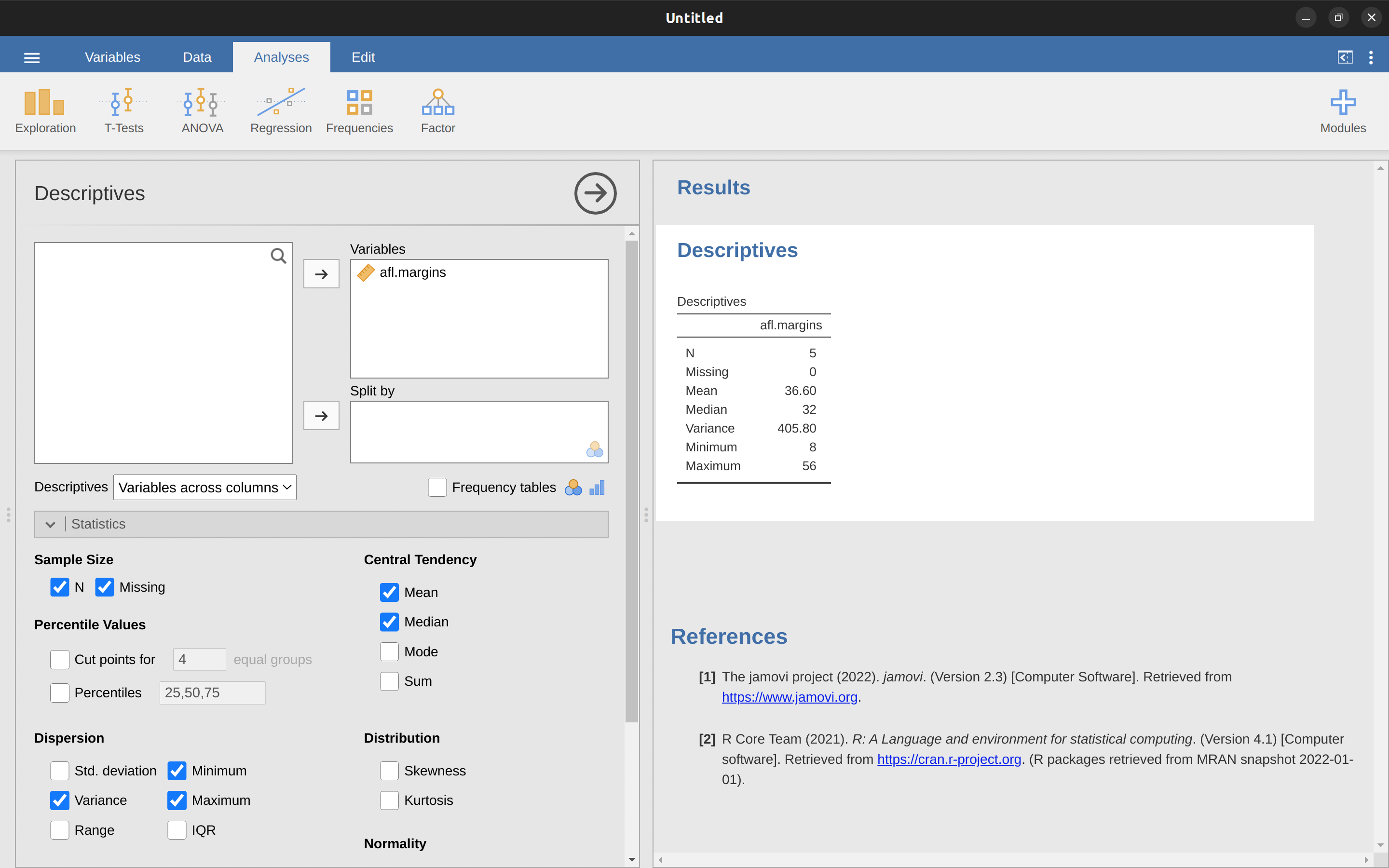
La respuesta es no.7 No es un error tipográfico y jamovi no está cometiendo un error. De hecho, es muy sencillo explicar lo que hace jamovi aquí, pero es un poco más complicado explicar por qué lo hace. Así que empecemos con el “qué”. Lo que jamovi está haciendo es evaluar una fórmula ligeramente diferente a la que te mostré anteriormente. En lugar de promediar las desviaciones al cuadrado, lo que requiere dividir por el número de puntos de datos N, jamovi eligió dividir por \(N - 1\).
[Detalle técnico adicional8]
Así que ese es el qué. La verdadera pregunta es por qué jamovi está dividiendo por \(N - 1\) y no por \(N\). Después de todo, se supone que la variancia es la desviación cuadrática media, ¿verdad? Entonces, ¿no deberíamos dividir por N, el número real de observaciones en la muestra? Bueno, sí, deberíamos. Sin embargo, como veremos en el capítulo sobre Chapter 8, existe una distinción sutil entre “describir una muestra” y “hacer conjeturas sobre la población de la que procede la muestra”. Hasta este punto, ha sido una distinción sin diferencia. Independientemente de si se describe una muestra o se hagan inferencias sobre la población, la media se calcula exactamente igual. No ocurre lo mismo con la variancia, la desviación estándar, o muchas otras medidas. Lo que describí anteriormente (es decir, tomar la media real y dividirla por \(N\)) asume que literalmente pretendes calcular la variancia de la muestra. Sin embargo, la mayoría de las veces, no te interesa la muestra en sí misma. Más bien, la muestra existe para decirte algo sobre el mundo. Si es así, estás comenzando a alejarte del cálculo de un “estadístico muestral” y acercándote a la idea de estimar un “parámetro poblacional”. Pero me estoy adelantando. Por ahora, confiemos en que jamovi sabe lo que hace, y revisaremos esta cuestión más adelante cuando hablemos de la estimación en Chapter 8.
Bien, una última cosa. Esta sección hasta ahora se ha leído un poco como una novela de misterio. Te he enseñado a calcular la variancia, he descrito el extraño “\(N - 1\)” que hace jamovi y he insinuado la razón por la que está ahí, pero no he mencionado lo más importante. ¿Cómo interpretas la variancia? Después de todo, se supone que la estadística descriptiva describe cosas, y ahora mismo la variancia no es más que un número incomprensible. Desafortunadamente, la razón por la que no te he dado una interpretación humana de la variancia es que realmente no existe. Este es el problema más grave de la variancia. Aunque tiene algunas propiedades matemáticas elegantes que sugieren que realmente es una cantidad fundamental para expresar la variación, es completamente inútil si quieres comunicarte con un ser humano real. Las variancias son completamente imposibles de interpretar en términos de la variable original. Todos los números se han elevado al cuadrado y ya no significan nada. Es un problema enorme. Por ejemplo, según Table 4.3, el margen del partido 1 fue “376,36 puntos cuadrados superior al margen medio”. Esto es exactamente tan estúpido como suena, y por eso cuando calculamos una variancia de \(324.64\) estamos en la misma situación. He visto muchos partidos de fútbol y en ningún momento nadie se ha referido a “puntos al cuadrado”. No es una unidad de medida real, y dado que la variancia se expresa en términos de esta unidad de galimatías, carece totalmente de sentido para un humano.
4.2.5 Desviación Estándar
De acuerdo, supongamos que te gusta la idea de utilizar la variancia por esas bonitas propiedades matemáticas de las que no he hablado, pero como eres un ser humano y no un robot, te gustaría tener una medida que se exprese en el mismas unidades que los propios datos (es decir, puntos, no puntos al cuadrado). ¿Qué debes hacer? La solución al problema es obvia. Tomar la raíz cuadrada de la variancia, conocida como desviación estándar, también llamada “raíz de la desviación cuadrática media”. Esto resuelve nuestro problema bastante bien. Aunque nadie tiene ni idea de lo que realmente significa “una variancia de 324,68 puntos al cuadrado”, es mucho más fácil entender “una desviación estándar de 18,01 puntos” ya que se expresa en las unidades originales. Es tradicional referirse a la desviación estándar de una muestra de datos como s, aunque a veces también se utilizan “de” y “desv est”.
[Detalle técnico adicional9]
Sin embargo, como habrás adivinado por nuestra discusión sobre la variancia, lo que jamovi calcula en realidad es ligeramente diferente a la fórmula anterior. Al igual que vimos con la variancia, lo que jamovi calcula es una versión que divide por \(N - 1\) en lugar de \(N\).
[Detalle técnico adicional10]
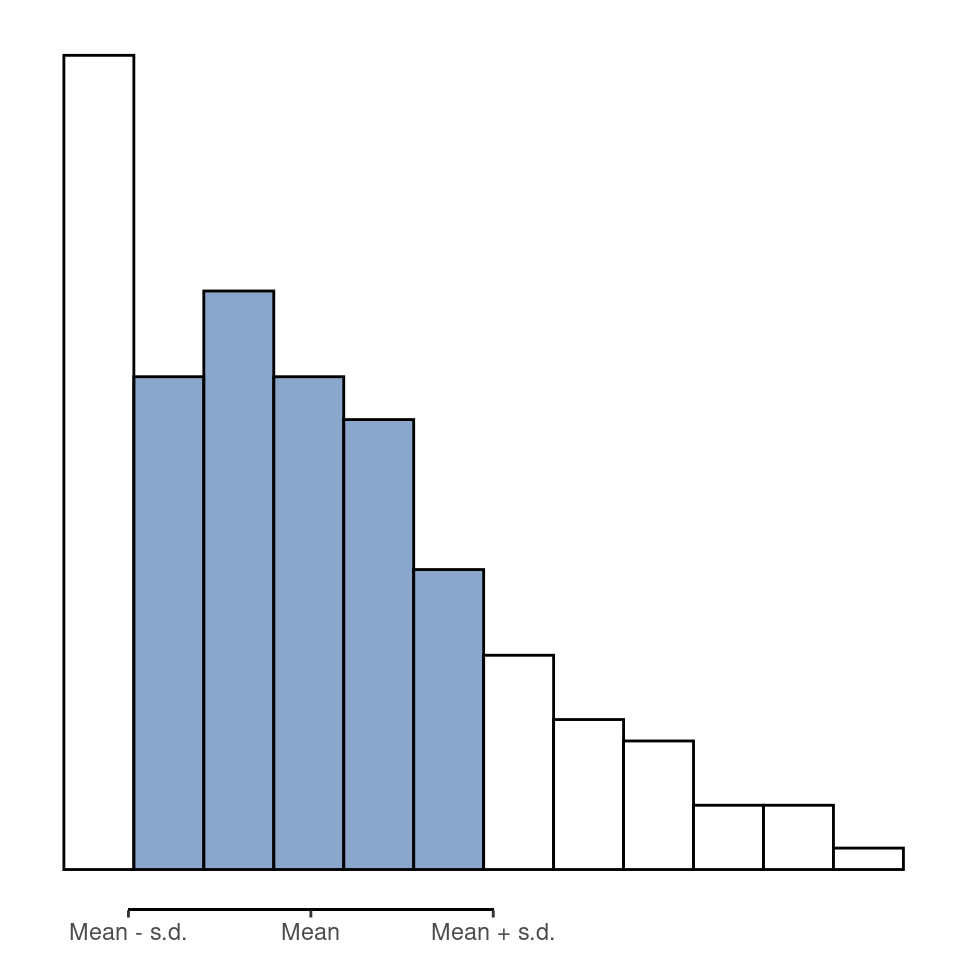
Interpretar las desviaciones estándar es un poco más complejo. Como la desviación estándar se obtiene a partir de la variancia, y la variancia es una cantidad que tiene poco o ningún significado para nosotros, los humanos, la desviación estándar no tiene una interpretación sencilla. En consecuencia, la mayoría de nosotras nos basamos en una simple regla empírica. En general, cabe esperar que el 68 % de los datos se sitúen dentro de 1 desviación estándar de la media, el 95 % de los datos dentro de 2 desviaciones estándar de la media y el 99,7 % de los datos dentro de 3 desviaciones estándar de la media. Esta regla suele funcionar bastante bien la mayoría de las veces, pero no es exacta. En realidad, se calcula basándose en la suposición de que el histograma es simétrico y tiene “forma de campana”.[^04.5] Como puedes ver en el histograma de márgenes ganadores de la AFL en Figure 4.2, esto no es exactamente cierto en nuestros datos. Aun así, la regla es aproximadamente correcta. Resulta que el 65,3 % de los datos de los márgenes de la AFL caen dentro de una desviación estándar de la media. Esto se muestra visualmente en Figure 4.10.
4.2.6 ¿Qué medida hay que utilizar?
Hemos discutido varias medidas de dispersión: rango, RIC, desviación absoluta media, variancia y desviación estándar; y hemos aludido a sus puntos fuertes y débiles. He aquí un resumen rápido:
- Rango. Proporciona la dispersión completa de los datos. Es muy vulnerable a los valores atípicos y, en consecuencia, no se suele utilizar a menos que haya buenas razones para preocuparse por los extremos de los datos.
- Rango intercuartílico. Indica dónde se sitúa la “mitad central” de los datos. Es bastante robusto y complementa muy bien a la mediana. Se usa mucho.
- Desviación media absoluta. Indica la distancia “media” entre las observaciones y la media. Es muy interpretable pero tiene algunos problemas menores (no discutidos aquí) que la hacen menos atractiva para los estadísticos que la desviación estándar. Se usa a veces, pero no a menudo.
- Variancia. Indica la desviación media al cuadrado de la media. Es matemáticamente elegante y probablemente la forma “correcta” de describir la variación alrededor de la media, pero es completamente ininterpretable porque no usa las mismas unidades que los datos. Casi nunca se usa excepto como una herramienta matemática, pero está oculta “bajo el capó” de una gran cantidad de herramientas estadísticas.
- Desviación Estándar. Es la raíz cuadrada de la variancia. Es bastante elegante desde el punto de vista matemático y se expresa en las mismas unidades que los datos, por lo que se puede interpretar bastante bien. En situaciones en las que la media es la medida de tendencia central, esta es la medida por defecto. Es, con mucho, la medida de variación más popular.
En resumen, el RIC y la desviación estándar son fácilmente las dos medidas más utilizadas para informar de la variabilidad de los datos. Pero hay situaciones en las que se utilizan las otras. Las he descrito todas en este libro porque es muy probable que te encuentres con la mayoría de ellas en alguna parte.
4.3 Asimetría y apuntamiento
Hay otros dos estadísticos descriptivos que a veces aparecen en la literatura psicológica: la asimetría y el apuntamiento. En la práctica, ninguno de los dos se usa con tanta frecuencia como las medidas de tendencia central y variabilidad de las que hemos hablado. La asimetría es bastante importante, por lo que se menciona a menudo, pero nunca he visto el apuntamiento en un artículo científico hasta la fecha.
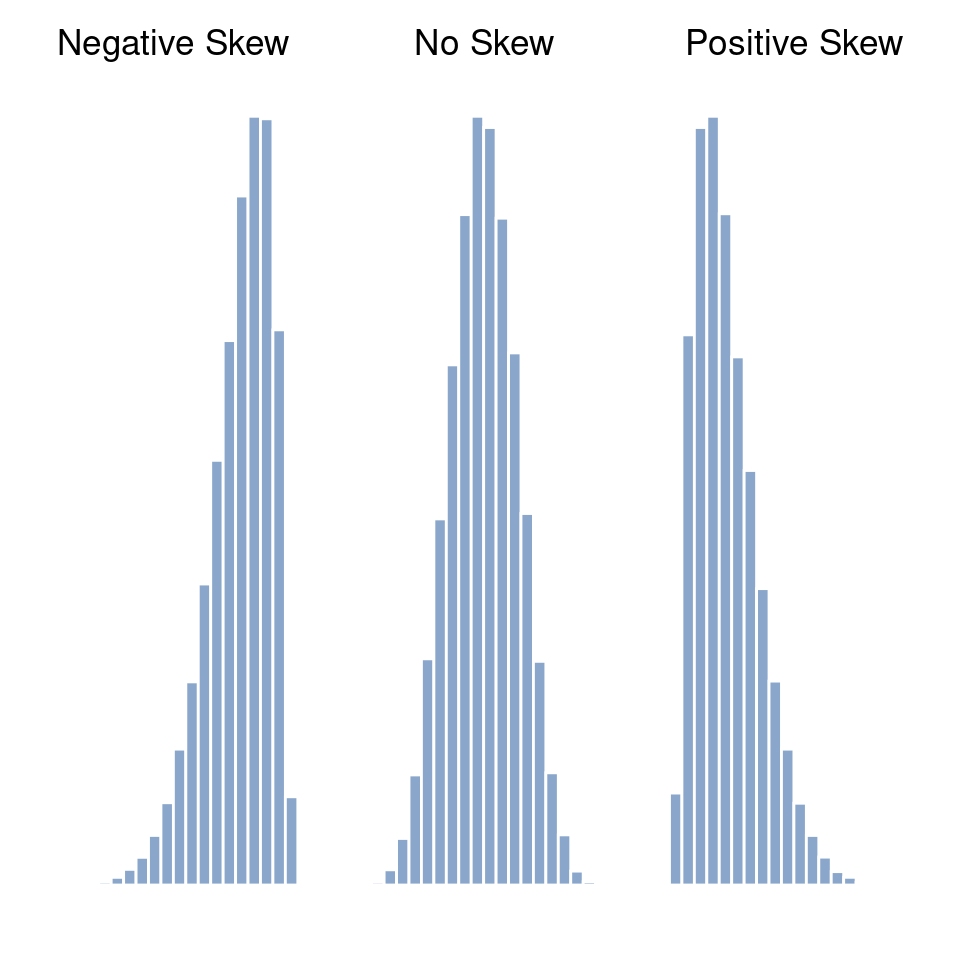
Como es el más interesante de los dos, comencemos hablando de la asimetría. La asimetría es básicamente una medida de asimetría y la forma más fácil de explicarla es haciendo algunos dibujos. Como ilustra Figure 4.11, si los datos tienden a tener muchos valores extremadamente pequeños (es decir, la cola inferior es “más larga” que la cola superior) y no tantos valores extremadamente grandes (panel izquierdo), entonces decimos que los datos presentan asimetría negativa. En cambio, si hay más valores extremadamente grandes que extremadamente pequeños (panel derecho), decimos que los datos presentan asimetría positiva. Esa es la idea cualitativa que subyace a la asimetría. Si hay relativamente más valores que son muy superiores a la media, la distribución tiene una asimetría positiva o una asimetría hacia la derecha, con una cola que se extiende hacia la derecha. La asimetría negativa o izquierda es lo contrario. Una distribución simétrica tiene una asimetría de 0. El valor de asimetría para una distribución con asimetría positiva es positivo y el valor para una distribución con asimetría negativa es negativo.
[Detalle técnico adicional11]
Quizás sea más útil usar jamovi para calcular la asimetría: es una casilla de verificación en las opciones de ‘Estadísticas’ en ‘Exploración’ - ‘Descriptivos’. Para la variable afl.margins, la asimetría es de \(0.780\). Si divides la estimación de la asimetría por el error estándar de la asimetría, tendrás una indicación del grado de asimetría de los datos. Especialmente en muestras pequeñas (N \(<\) 50), una regla general sugiere que un valor de 2 o menos puede significar que los datos no son muy asimétricos, y un valor de más de 2 sugiere que hay suficiente asimetría en los datos para posiblemente limitar su uso en algunos análisis estadísticos. Aunque no hay un acuerdo claro sobre esta interpretación. Dicho esto, esto indica que los datos de márgenes ganadores de la AFL son algo asimétricos (\(\frac{0.780}{0.183} = 4.262\)).
La última medida a la que a veces se hace referencia, aunque muy raramente en la práctica, es el apuntamiento de un conjunto de datos. En pocas palabras, el apuntamiento es una medida de lo delgadas o gruesas que son las colas de una distribución, como se ilustra en Figure 4.12. Por convención, decimos que la “curva normal” (líneas negras) tiene apuntamiento cero, por lo que el grado de apuntamiento se evalúa en relación con esta curva.
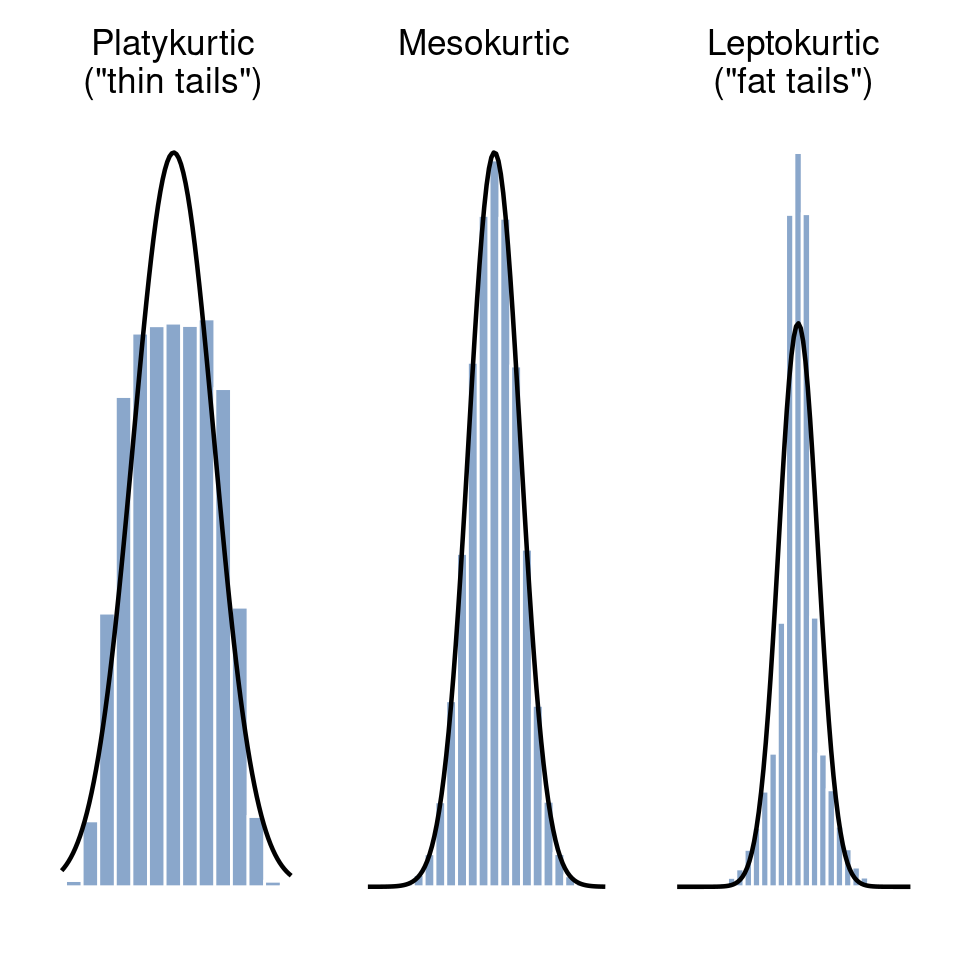
En esta figura, los datos de la izquierda tienen una distribución bastante plana, con colas finas, por lo que el apuntamiento es negativo y decimos que los datos son platicúrticos. Los datos de la derecha tienen una distribución con colas gruesas, por lo que el apuntamiento es positivo y decimos que los datos son leptocúrticos. Pero los datos del medio no tienen colas gruesas ni gordas, por lo que decimos que son mesocúrticos y tienen apuntamiento cero. Esto se resume en Table 4.4:
| English | informal term | kurtosis value |
|---|---|---|
| "tails too thin" | platykurtic | negative |
| "tails neither thin or fat" | mesokurtic | zero |
| "tails too fat" | leptokurtic | positive |
[Detalle técnico adicional12]
Más concretamente, jamovi tiene una casilla de verificación para el apuntamiento justo debajo de la casilla de verificación para la asimetría, y esto da un valor para el apuntamiento de \(0.101\) con un error estándar de \(0.364\). Esto significa que los datos de márgenes ganadores de la AFL tienen solo un pequeño apuntamiento, lo cual está bien.
4.4 Estadísticos descriptivos para cada grupo
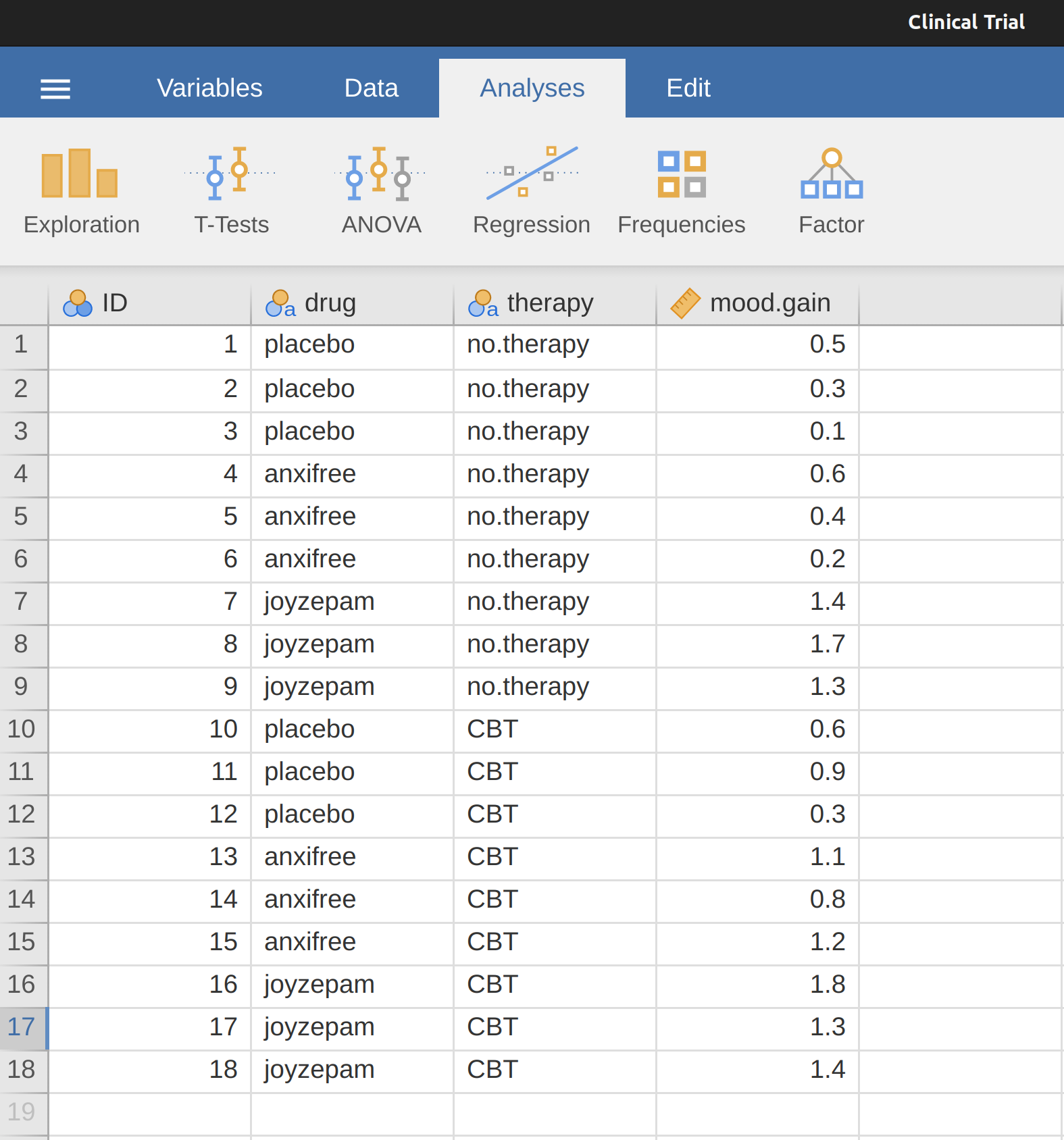
Es muy frecuente encontrarse con la necesidad de consultar estadísticos descriptivos desglosados por alguna variable de agrupación. Esto es bastante fácil de hacer en jamovi. Por ejemplo, supongamos que quiero ver los estadísticos descriptivos de algunos datos de ensayos clínicos, desglosados por separado según el tipo de terapia. Se trata de un nuevo conjunto de datos, que no habías visto antes. Los datos están almacenados en el archivo Clinicaltrial.csv y los usaremos mucho más adelante en Chapter 13 (puedes encontrar una descripción completa de los datos al principio de ese capítulo). Vamos a cargarlo y ver lo que tenemos (Figure 4.13):
Evidentemente, había tres fármacos: un placebo, algo llamado “anxifree” y algo llamado “joyzepam”, y cada fármaco se le administró a 6 personas. Hubo 9 personas tratadas con terapia cognitiva conductual (TCC) y 9 personas que no recibieron tratamiento psicológico. Y podemos ver al mirar las ‘Descriptivas’ de la variable mood.gain que la mayoría de las personas mostraron una mejora en el estado de ánimo (\(media = 0.88\)), aunque sin saber cuál es la escala aquí es difícil decir mucho más que eso. Aún así, no está nada mal. En general, creo que he aprendido algo.
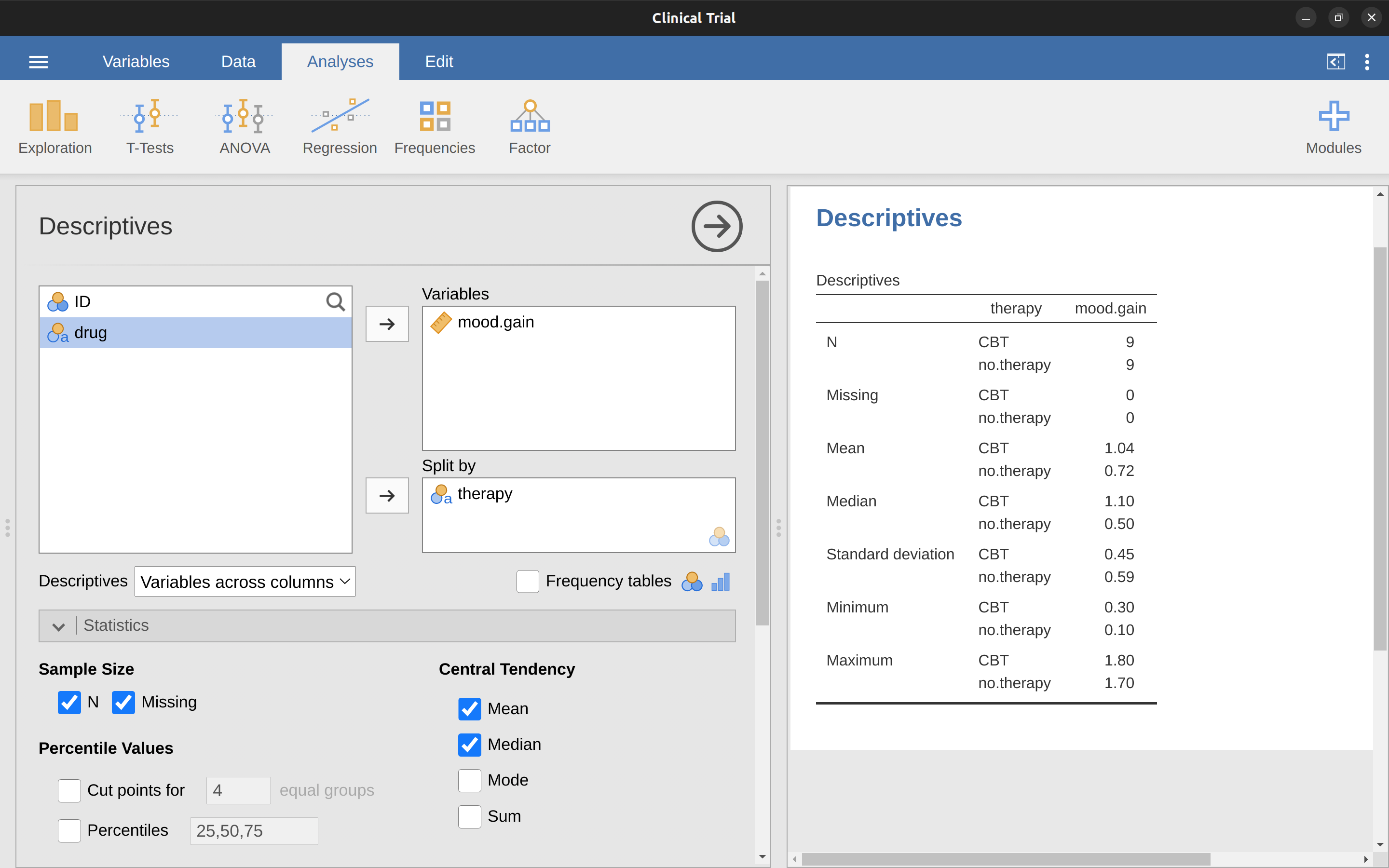
También podemos seguir adelante y ver otros estadísticos descriptivos, y esta vez por separado para cada tipo de terapia. En jamovi, marca Desviación Estándar, Asimetría y Apuntamiento en las opciones de ‘Estadísticas’. Al mismo tiempo, mueve la variable de terapia al cuadro ‘Dividir por’ y deberías obtener algo como Figure 4.14.
¿Qué ocurre si tienes múltiples variables de agrupación? Supongamos que deseas observar el aumento medio del estado de ánimo por separado para todas las combinaciones posibles de fármaco y terapia. Es posible hacerlo añadiendo otra variable, fármaco, en el cuadro ‘Dividir por’. Fácil, aunque a veces si divides demasiado no hay suficientes datos en cada combinación de desglose para hacer cálculos significativos. En este caso, jamovi lo indica diciendo algo como NaN o Inf. 13
4.5 Puntuaciones estándar
Supongamos que mi amigo está elaborando un nuevo cuestionario destinado a medir el “mal humor”. La encuesta tiene \(50\) preguntas a las que puedes responder de forma malhumorada o no. En una muestra grande (hipotéticamente, imaginemos un millón de personas más o menos) los datos se distribuyen de forma bastante normal: la puntuación media de mal humor es de \(17\) de cada $50 preguntas respondidas de forma malhumorada, y la desviación estándar es de \(5\). En cambio, cuando hago el cuestionario respondo \(35\) de \(50\) preguntas de una forma malhumorada. Entonces, ¿hasta qué punto soy gruñona? Una forma de verlo sería decir que tengo un mal humor de \(\frac{35}{50}\), por lo que podría decir que soy un 70% gruñona. Pero eso es un poco raro, si lo piensas. Si mi amigo hubiera formulado sus preguntas de otra manera, la gente podría haberlas respondido de una manera diferente, por lo que la distribución general de las respuestas podría subir o bajar dependiendo de la forma precisa en que se formularan las preguntas. Por lo tanto, solo tengo un 70% de mal humor con respecto a este conjunto de preguntas de la encuesta. Incluso si fuera un cuestionario muy bueno, no es una afirmación muy informativa.
Una forma más sencilla de describir mi mal humor es compararme con otras personas. Sorprendentemente, de la muestra de mi amigo de \(1,000,000\) de personas, solo \(159\) personas eran tan malhumoradas como yo (lo cual no es nada irreal, francamente) lo que sugiere que estoy en el 0.016% superior de la gente malhumorada. Esto tiene mucho más sentido que intentar interpretar los datos en bruto. Esta idea, la de que deberíamos describir mi mal humor en términos de la distribución general del mal humor de los seres humanos, es la idea cualitativa a la que intenta llegar la estandarización. Una forma de hacerlo es hacer exactamente lo que acabo de mostrar y describirlo todo en términos de percentiles. Sin embargo, el problema es que “estás solo en la cima”. Supongamos que mi amigo solo había recogido una muestra de \(1000\) personas (todavía es una muestra bastante grande a efectos de probar un nuevo cuestionario, me gustaría añadir), y esta vez hubiera obtenido, digamos, una media de \(16\) sobre \(50\) con una desviación estándar de \(5\). El problema es que es casi con toda seguridad ni una sola persona en esa muestra sería tan gruñona como yo.
Sin embargo, no todo está perdido. Un enfoque diferente es convertir mi puntuación de mal humor en una puntuación estándar, también conocida como puntuación z. La puntuación estándar se define como el número de desviaciones estándar por encima de la media en la que se encuentra mi puntuación de mal humor. Para expresarlo en “pseudomatemáticas”, la puntuación estándar se calcula así:
\[ \text{puntaje estándar} = \frac{\text{puntaje bruto} - media}{\text{desviación estándar}} \]
[Detalle técnico adicional14]
Así que, volviendo a los datos de mal humor, ahora podemos transformar el mal humor en bruto de Dani en una puntuación de mal humor estandarizada.
\[ z =\frac{35 - 17}{5} = 3,6 \] Para interpretar este valor, recuerda la heurística aproximada que proporcioné en la sección sobre Desviación estándar en la que señalé que se espera que el 99,7 % de los valores se encuentran dentro de 3 desviaciones estándar de la media. Así que el hecho de que mi mal humor corresponda a una puntuación z de 3,6 indica que soy muy gruñona. De hecho, esto sugiere que soy más gruñóna que el 99,98% de las personas. Me parece correcto.
Además de permitirte interpretar una puntuación bruta en relación con una población más amplia (y, por tanto, darle sentido a variables que se sitúan en escalas arbitrarias), las puntuaciones estándar cumplen una segunda función útil. Las puntuaciones estándar se pueden comparar entre sí en situaciones en las que las puntuaciones brutas no pueden. Supongamos, por ejemplo, que mi amigo también tiene otro cuestionario que mide la extraversión utilizando un cuestionario de \(24\) ítems. La media general de esta medida resulta ser 13 con una desviación estándar de \(4\) y yo obtuve una puntuación de \(2\). Como puedes imaginar, no tiene mucho sentido intentar comparar mi puntuación bruta de \(2\) en el cuestionario de extraversión con mi puntuación bruta de 35 en el cuestionario de mal humor. Las puntuaciones brutas para las dos variables son “sobre” cosas fundamentalmente diferentes, así que sería como comparar manzanas con naranjas.
¿Y las puntuaciones estándar? Bueno, esto es un poco diferente. Si calculamos las puntuaciones estándar obtenemos \((z = \frac{(35-17)}{5}=3,6)\) para el mal humor y \((z = \frac{(2-13)}{4}=-2,75 )\) para la extraversión. Estos dos números se pueden comparar entre sí.15 Soy mucho menos extrovertida que la mayoría de la gente (\(z = -2,75\)) y mucho más gruñóna que la mayoría de la gente (\(z=3,6\)). Pero el alcance de mi rareza es mucho más extremo en el caso del mal humor, ya que \(3,6\) es un número mayor que \(2,75\). Dado que cada puntuación estandarizada es una afirmación sobre el lugar que ocupa una observación en relación con su propia población, es posible comparar puntuaciones estandarizados entre variables completamente diferentes.
4.6 Resumen
Calcular algunos estadísticos descriptivos básicos es una de las primeras cosas que se hacen cuando se analizan datos reales, y los estadísticos descriptivos son mucho más sencillos de entender que los estadísticaos inferenciales, así que, como cualquier otro libro de texto de estadística, he empezado con los descriptivos. En este capítulo, hablamos de los siguientes temas:
- Medidas de tendencia central. En términos generales, las medidas de tendencia central indican dónde se encuentran los datos. Hay tres medidas que suelen aparecer en la literatura: la media, la mediana y la moda.
- Medidas de variabilidad. Por el contrario, las medidas de variabilidad indican la “dispersión” de los datos. Las medidas clave son: rango, desviación estándar y rango intercuartílico.
- Asimetría y apuntamiento. También analizamos la asimetría en la distribución de una variable y las distribuciones con colas finas o gruesas (apuntamiento).
- Estadísticos descriptivos para cada grupo. Dado que este libro se centra en el análisis de datos en jamovi, dedicamos un poco de tiempo a hablar de cómo se calculan los estadísticos descriptivos para los diferentes subgrupos.
- Puntuaciones estándar. La puntuación z es una bestia un poco inusual. No es exactamente un estadístico descriptivo ni tampoco una inferencia. Asegúrate de entender esta sección. Volverá a aparecer más adelante.
En el próximo capítulo hablaremos de cómo hacer dibujos. A todo el mundo le gustan los dibujos bonitos, ¿verdad? Pero antes quiero terminar con un punto importante. Un primer curso tradicional de estadística dedica solo una pequeña parte de la clase a la estadística descriptiva, tal vez una o dos clases como mucho. La inmensa mayoría del tiempo del profesorado se dedica a la estadística inferencial porque ahí es donde está todo lo difícil. Eso tiene sentido, pero oculta la importancia práctica cotidiana de elegir buenos descriptivos. Teniendo esto en cuenta…
Nota para los no australianos: la AFL es una competición de fútbol de reglas australianas. No es necesario saber nada sobre las reglas australianas para seguir esta sección.↩︎
Bien, ahora intentemos escribir una fórmula para la media. Por tradición, usamos \(\bar{X}\) como notación para la media. Así que el cálculo de la media podría expresarse mediante la siguiente fórmula: \[\bar{X}=\frac{X_1 + X_2 ... + X_{N-1} + X_{N}}{N}\] Esta fórmula es completamente correcta pero es terriblemente larga, por lo que usamos el símbolo del sumatorio \(\sum\) para acortarla.\(^a\) Si quiero sumar las cinco primeras observaciones, podría escribir la suma de la forma larga, \(X_1 + X_2 + X_3 + X_4 + X_5\) o podría usar el símbolo de suma para acortarla a esto: \[\sum_{i=1}^{5} X_i\] Tomado al pie de la letra, esto podría leerse como “la suma, tomada sobre todos los valores i del 1 al 5, del valor \(X_i\)”. Pero básicamente lo que significa es “sumar las primeras cinco observaciones”. En cualquier caso, podemos usar esta notación para escribir la fórmula de la media, que tiene este aspecto: \[\bar{X}=\frac{1}{N}\sum_{i=1}^{N} X_i\] Sinceramente, no creo que toda esta notación matemática ayude a aclarar el concepto de la media en absoluto. De hecho, no es más que una forma elegante de escribir lo mismo que dije con palabras: sumar todos los valores y dividirlos por el número total de elementos. Sin embargo, esa no es realmente la razón por la que entré en tanto detalle. Mi objetivo era tratar de asegurarme de que todo el mundo leyendo este libro tenga clara la notación que usaremos a lo largo del mismo: \(\bar{X}\) para la media, \(\sum\) para la idea del sumatorio, $ X_i$ para la i-ésima observación y \(N\) para el número total de observaciones. Vamos a reutilizar estos símbolos un poco, por lo que es importante que los entiendas lo suficientemente bien como para poder “leer” las ecuaciones y poder ver que solo está diciendo “suma muchas cosas y luego divide por otra cosa”.
—
\(^a\) La elección de usar \(\sum\) para denotar el sumatorio no es arbitraria. Es la letra mayúscula griega sigma, que es el análogo de la letra \(S\) en ese alfabeto. De manera similar, hay un símbolo equivalente que se usa para denotar la multiplicación de muchos números, dado que las multiplicaciones también se llaman “productos” usamos el símbolo \(\prod\) para esto (la pi mayúscula griega, que es el análogo de la letra \(P\)).↩︎Sin embargo, aunque nuestros cálculos para este pequeño ejemplo han llegado a su fin, nos quedan un par de cosas de las que hablar. En primer lugar, deberíamos intentar escribir una fórmula matemática adecuada. Pero para ello necesito una notación matemática para referirme a la desviación absoluta media. “Desviación absoluta media” y “desviación absoluta mediana” tienen el mismo acrónimo (MAD en inglés), lo que genera cierta ambigüedad, así que mejor me invento algo diferente para la desviación absoluta media. Lo que haré es usar DAP en su lugar, abreviatura de desviación absoluta promedio. Ahora que tenemos una notación inequívoca, esta es la fórmula que describe lo que acabamos de calcular: \[AAD(X) =\frac{1}{N} \sum_{i=1}^{N} \mid X_i - \bar {X} \mid = 15.52\]↩︎
Bueno, mencionaré muy brevemente la que me parece más guay, para una definición muy particular de “guay”, claro. Las variancias son aditivas. Esto es lo que eso significa. Supongamos que tengo dos variables \(X\) y \(Y\), cuyas variancias son \(Var(X)\) y \(Var(Y)\) respectivamente. Ahora imagina que quiero definir una nueva variable Z que sea la suma de las dos, \(Z = X + Y\). Resulta que la variancia de \(Z\) es igual a \(Var(X) + Var(Y)\). Esta es una propiedad muy útil, pero no es cierta para las otras medidas de las que hablo en esta sección.↩︎
La fórmula que usamos para calcular la variancia de un conjunto de observaciones es la siguiente: \[VAR(X) =\frac{1}{N} \sum_{i=1}^{N} ( X_i - \bar{X} )^2\] Como puedes ver, es básicamente la misma fórmula que usamos para calcular la desviación absoluta media, salvo que en lugar de usar “desviaciones absolutas” usamos “desviaciones al cuadrado”. Es por esta razón que la variancia a veces se denomina “desviación cuadrática media”.↩︎
Con la posible excepción de la tercera pregunta.↩︎
En otras palabras, la fórmula que está usando jamovi es esta: \[\frac{1}{N-1} \sum_{i=1}^{N} ( X_i - \bar{X} )^2\]↩︎
dado que la desviación estándar es igual a la raíz cuadrada de la variancia, probablemente no te sorprenda ver que la fórmula es: \[s=\sqrt{\frac{1 }{N} \sum_{i=1}^{N} ( X_i - \bar{X} )^2 }\] y en jamovi hay una casilla de verificación para ‘Desv. Estándar’ justo encima de la casilla de verificación de ‘Variancia’. Al seleccionarla se obtiene un valor de \(26.07\) para la desviación estándar.↩︎
Por razones que tendrán sentido cuando volvamos a este tema en el capítulo sobre [Estimación de cantidades desconocidas de una muestra] me referiré a esta nueva cantidad como \(\hat{ \sigma}\) (léase como: “sombrero sigma”), y la fórmula para esto es: \[\hat{\sigma}=\sqrt{\frac{1}{N-1} \sum_{i=1} ^{N} ( X_i - \bar{X} )^2}\]↩︎
Una fórmula para la asimetría de un conjunto de datos es la siguiente \[ asimetría(X)=\frac{1}{N \hat{\sigma}^3} \sum_{i =1}^{N} ( X_i - \bar{X})^3\] donde N es el número de observaciones, \(\bar{X}\) es la media muestral y \(\hat{\sigma}\) es la desviación estándar (es decir, la versión “dividir por \(N - 1\)”).↩︎
La ecuación para el apuntamiento es bastante similar en espíritu a las fórmulas que ya hemos visto para la variancia y la asimetría. Salvo que donde la variancia incluía desviaciones al cuadrado y la asimetría incluía desviaciones al cubo, la curtosis implica elevar las desviaciones a la cuarta potencia: \(^b\) \[curtosis(X)=\frac{1}{N \hat{\sigma} ^4} \sum_{i=1}^{N} ( X_i - \bar{X} )^4 - 3\] Lo sé, a mí tampoco me interesa mucho.
—
\(^b\) El “-3” es algo que los estadísticos añaden para asegurarse de que la curva normal tenga un apuntamiento cero. Parece un poco estúpido poner un “-3” al final de la fórmula, pero existen buenas razones matemáticas para hacerlo.↩︎A veces, jamovi también presenta los números de una forma inusual. Si un número es muy pequeño, o muy grande, jamovi cambia a una forma exponencial. Por ejemplo, 6,51e-4 es lo mismo que decir que el punto decimal se mueve 4 posiciones a la izquierda, por lo que el número real es 0,000651. Si hay un signo más (es decir, 6,51e+4), entonces el punto decimal se desplaza hacia la derecha, es decir, 65.100,00. Normalmente, solo se expresan de este modo los números muy pequeños o muy grandes, por ejemplo, 6,51e-16, que sería bastante difícil de escribir de la manera normal.↩︎
En matemáticas reales, la ecuación para la puntuación z es \[z_i =\frac{X_i - \bar{X}}{\hat{\sigma}}\]↩︎
Aunque suele estar justificada con cautela. No siempre se da el caso de que una desviación estándar en la variable A corresponda al mismo “tipo” de cosas que una desviación estándar en la variable B. Usa el sentido común cuando intentes determinar si las puntuaciones z de dos variables se pueden comparar significativamente o no.↩︎