15 Análisis factorial
Los capítulos anteriores han cubierto las pruebas estadísticas para las diferencias entre dos o más grupos. Sin embargo, a veces, cuando realizamos una investigación, es posible que deseemos examinar cómo múltiples variables co-varían. Es decir, cómo se relacionan entre sí y si los patrones de relación sugieren algo interesante y significativo. Por ejemplo, a menudo nos interesa explorar si hay factores latentes no observados subyacentes que están representados por las variables observadas, medidas directamente, en nuestro conjunto de datos. En estadística, los factores latentes son inicialmente variables ocultas que no se observan directamente, sino que se infieren (a través del análisis estadístico) de otras variables que se observan (medidas directamente).
En este capítulo consideraremos una serie de análisis factorial diferentes y técnicas relacionadas, comenzando con Análisis factorial exploratorio (AFE). EFA es una técnica estadística para identificar factores latentes subyacentes en un conjunto de datos. Luego cubriremos Análisis de componentes principales (PCA), que es una técnica de reducción de datos que, estrictamente hablando, no identifica los factores latentes subyacentes. En cambio, PCA simplemente produce una combinación lineal de variables observadas. Después de esto, la sección sobre Análisis factorial confirmatorio (CFA) muestra que, a diferencia de EFA, con CFA se comienza con una idea, un modelo, de cómo las variables en sus datos se relacionan entre sí. Luego, prueba tu modelo con los datos observados y evalúa qué tan bueno es el ajuste del modelo. Una versión más sofisticada de CFA es el llamado enfoque [Multi-Trait Multi-Method CFA] en el que tanto el factor latente como la varianza del método se incluyen en el modelo. Esto es útil cuando se utilizan diferentes enfoques metodológicos para la medición y, por lo tanto, la variación del método es una consideración importante. Finalmente, cubriremos un análisis relacionado: Análisis de confiabilidad de consistencia interna prueba cuán consistentemente una escala mide una construcción psicológica.
15.1 Análisis factorial exploratorio
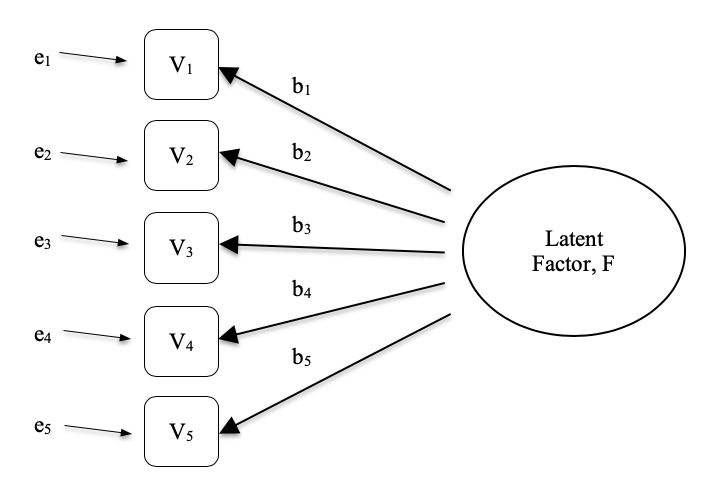
Análisis factorial exploratorio (AFE) es una técnica estadística para revelar cualquier factor latente oculto que se pueda inferir de nuestros datos observados. Esta técnica calcula hasta qué punto un conjunto de variables medidas, por ejemplo, \(V1, V2, V3, V4\) y \(V5\), pueden representarse como medidas de un factor latente subyacente. Este factor latente no puede medirse a través de una sola variable observada sino que se manifiesta en las relaciones que provoca en un conjunto de variables observadas.
En Figure 15.1 cada variable observada \(V\) es ‘causada’ hasta cierto punto por el factor latente subyacente (\(F\)), representado por los coeficientes \(b_1\) a \(b_5\) (también llamados factores de carga). Cada variable observada también tiene un término de error asociado, e1 a e5. Cada término de error es la varianza en la variable observada asociada, \(V_i\) , que no se explica por el factor latente subyacente.
En Psicología, los factores latentes representan fenómenos o construcciones psicológicas que son difíciles de observar o medir directamente. Por ejemplo, personalidad, inteligencia o estilo de pensamiento. En el ejemplo de Figure 15.1, es posible que le hayamos hecho a las personas cinco preguntas específicas sobre su comportamiento o actitudes, y de eso podemos obtener una imagen sobre una construcción de personalidad llamada, por ejemplo, extraversión. Un conjunto diferente de preguntas específicas puede darnos una idea sobre la introversión de un individuo o su escrupulosidad.
Aquí hay otro ejemplo: es posible que no podamos medir directamente la ansiedad estadística, pero podemos medir si la ansiedad estadística es alta o baja con un conjunto de preguntas en un cuestionario. Por ejemplo, “\(Q1\): Hacer la tarea para un curso de estadística”, “\(Q2\): Tratar de comprender las estadísticas descritas en un artículo de revista” y “\(Q3\): Solicitar ayuda al profesor para comprender algo del curso”, etc., cada uno calificado de baja ansiedad a alta ansiedad. Las personas con alta ansiedad estadística tenderán a dar respuestas igualmente altas en estas variables observadas debido a su alta ansiedad estadística. Del mismo modo, las personas con ansiedad estadística baja darán respuestas bajas similares a estas variables debido a su ansiedad estadística baja.
En el análisis factorial exploratorio (AFE), esencialmente estamos explorando las correlaciones entre las variables observadas para descubrir cualquier factor subyacente (latente) interesante e importante que se identifique cuando las variables observadas covarían. Podemos usar software estadístico para estimar cualquier factor latente e identificar cuáles de nuestras variables tienen una carga alta1 (por ejemplo, carga > 0.5) en cada factor, lo que sugiere que son una medida útil o indicador de el factor latente. Parte de este proceso incluye un paso llamado rotación, que para ser honesto es una idea bastante extraña pero afortunadamente no tenemos que preocuparnos por entenderlo; solo necesitamos saber que es útil porque hace que el patrón de cargas en diferentes factores sea mucho más claro. Como tal, la rotación ayuda a ver con mayor claridad qué variables están vinculadas sustancialmente a cada factor. También necesitamos decidir cuántos factores son razonables dados nuestros datos, y útil en este sentido es algo llamado valores propios. Volveremos a esto en un momento, después de que hayamos cubierto algunos de los principales supuestos de la EPT.
15.1.1 Comprobación de supuestos
Hay un par de suposiciones que deben verificarse como parte del análisis. La primera suposición es esfericidad, que esencialmente verifica que las variables en su conjunto de datos estén correlacionadas entre sí en la medida en que puedan resumirse potencialmente con un conjunto más pequeño de factores. La prueba de esfericidad de Bartlett verifica si la matriz de correlación observada diverge significativamente de una matriz de correlación cero (o nula). Entonces, si la prueba de Bartlett es significativa (\(p < .05\)), esto indica que la matriz de correlación observada es significativamente divergente de la nula y, por lo tanto, es adecuada para EFA.
La segunda suposición es la adecuación del muestreo y se verifica utilizando la Medida de Adecuación del Muestreo (MSA) de Kaiser-MeyerOlkin (KMO). El índice KMO es una medida de la proporción de varianza entre las variables observadas que podría ser una varianza común. Usando correlaciones parciales, busca factores que carguen solo dos elementos. Rara vez, si acaso, queremos que EFA produzca muchos factores cargando solo dos elementos cada uno. KMO se trata de la adecuación del muestreo porque las correlaciones parciales generalmente se ven con muestras inadecuadas. Si el índice KMO es alto (\(\approx 1\)), el EFA es eficiente, mientras que si KMO es bajo (\(\approx 0\)), el EFA no es relevante. Los valores de KMO inferiores a \(0,5\) indican que EFA no es adecuado y debe haber un valor de KMO de \(0,6\) antes de que EFA se considere adecuado. Los valores entre \(0,5\) y \(0,7\) se consideran adecuados, los valores entre \(0,7\) y \(0,9\) son buenos y los valores entre \(0,9\) y \(1,0\) son excelentes.
15.1.2 ¿Para qué sirve la EPT?
Si la EFA ha brindado una buena solución (es decir, un modelo de factores), entonces debemos decidir qué hacer con nuestros nuevos y brillantes factores. Los investigadores a menudo usan EFA durante el desarrollo de escalas psicométricas. Desarrollarán un conjunto de elementos del cuestionario que creen que se relacionan con uno o más constructos psicológicos, usarán EFA para ver qué elementos “van juntos” como factores latentes y luego evaluarán si algunos elementos deben eliminarse porque no son útiles. o medir claramente uno de los factores latentes.
De acuerdo con este enfoque, otra consecuencia de EFA es combinar las variables que se cargan en distintos factores en un puntaje de factor, a veces conocido como puntaje de escala. Hay dos opciones para combinar variables en una puntuación de escala:
- Crear una nueva variable con una puntuación ponderada por las cargas factoriales de cada elemento que contribuye al factor.
- Crear una nueva variable a partir de cada ítem que contribuya al factor, pero ponderándolos por igual.
En la primera opción, la contribución de cada ítem a la puntuación combinada depende de qué tan fuertemente se relacione con el factor. En la segunda opción, generalmente solo promediamos todos los elementos que contribuyen sustancialmente a un factor para crear la variable de puntuación de escala combinada. Cuál elegir es una cuestión de preferencia, aunque una desventaja con la primera opción es que las cargas pueden variar bastante de una muestra a otra, y en las ciencias del comportamiento y de la salud, a menudo estamos interesados en desarrollar y usar puntajes de escala de cuestionarios compuestos en diferentes estudios. y diferentes muestras. En cuyo caso, es razonable utilizar una medida compuesta que se base en los elementos sustantivos que contribuyen por igual en lugar de ponderar por cargas específicas de muestra de una muestra diferente. En cualquier caso, entender una medida de variable combinada como un promedio de elementos es más simple e intuitivo que usar una combinación ponderada óptimamente específica de una muestra.
Una técnica estadística más avanzada, que está más allá del alcance de este libro, emprende el modelado de regresión donde los factores latentes se utilizan en modelos de predicción de otros factores latentes. Esto se denomina “modelado de ecuaciones estructurales” y existen programas de software específicos y paquetes R dedicados a este enfoque. Pero no nos adelantemos; en lo que realmente deberíamos centrarnos ahora es en cómo hacer un EFA en jamovi.
15.1.3 EPT en Jamovi
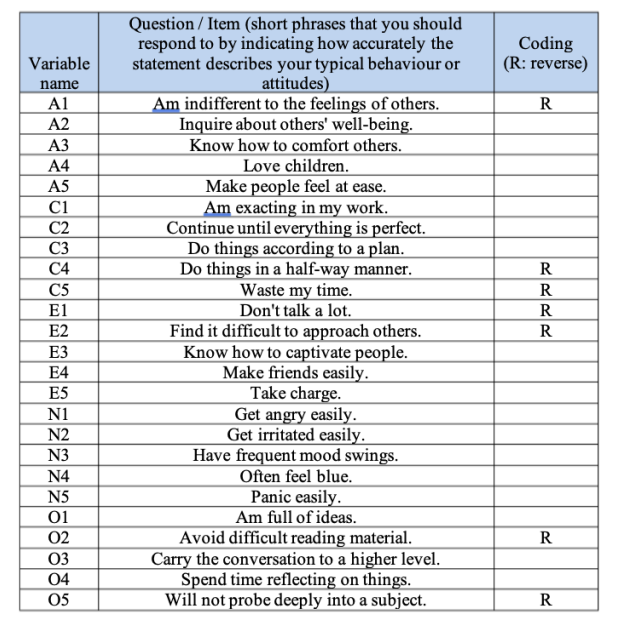
Primero, necesitamos algunos datos. Veinticinco ítems de autoinforme de personalidad (ver Figure 15.2) tomados del International Personality Item Pool fueron incluido como parte de la evaluación de personalidad basada en la web de Evaluación de personalidad de apertura sintética (SAPA) (SAPA: http://sapa-project.org) proyecto. Los 25 ítems están organizados por cinco factores putativos: Amabilidad, Escrupulosidad, Extraversión, Neuroticismo y Apertura.
Los datos de los ítems se recopilaron utilizando una escala de respuesta de 6 puntos:
- Muy impreciso
- Moderadamente impreciso
- Ligeramente impreciso
- Ligeramente preciso
- Moderadamente preciso
- Muy preciso.
Una muestra de \(N=250\) respuestas está contenida en el conjunto de datos bfi_sample.csv. Como investigadores, estamos interesados en explorar los datos para ver si hay algunos factores latentes subyacentes que se miden razonablemente bien con las variables observadas de \(25\) en el archivo de datos bfi_sample.csv. Abra el conjunto de datos y verifique que las variables de \(25\) estén codificadas como variables continuas (técnicamente, son ordinales, aunque para EFA en jamovi en general no importa, excepto si decide calcular puntajes de factores ponderados, en cuyo caso se necesitan variables continuas) . Para realizar EFA en jamovi:
Seleccione Factor - Análisis factorial exploratorio en la barra de botones principal de jamovi para abrir la ventana de análisis EFA (Figure 15.3).
Seleccione las 25 preguntas de personalidad y transfiéralas al cuadro ‘Variables’.
Marque las opciones apropiadas, incluidas las ‘Comprobaciones de suposiciones’, pero también las opciones de ‘Método’ de rotación, ‘Número de factores’ para extraer y ‘Salida adicional’. Consulte Figure 15.3 para ver las opciones sugeridas para este EFA ilustrativo, y tenga en cuenta que el ‘Método’ de rotación y el ‘Número de factores’ extraídos normalmente los ajusta el investigador durante el análisis para encontrar el mejor resultado, como se describe a continuación.

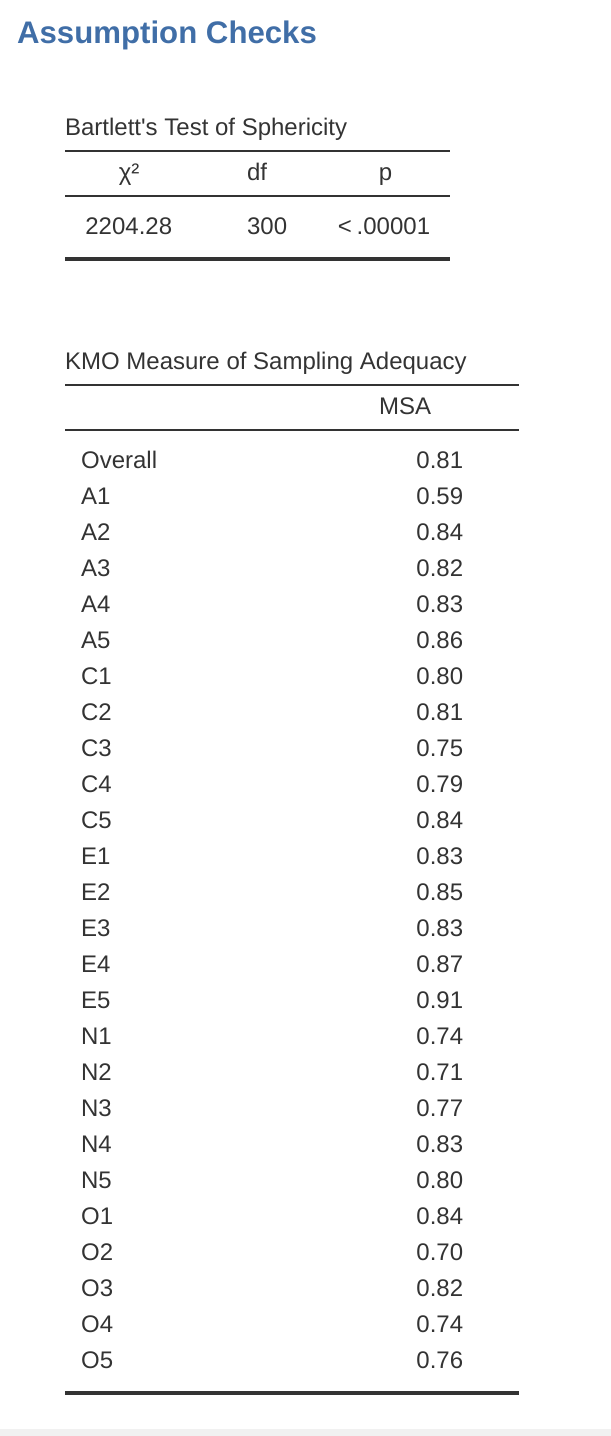
Primero, verifique las suposiciones (Figure 15.4). Puede ver que (1) la prueba de esfericidad de Bartlett es significativa, por lo que se cumple esta suposición; y (2) la medida de adecuación del muestreo (MSA) de KMO es de $ 0.81 $ en general, lo que sugiere una buena adecuación del muestreo. No hay problemas aquí entonces!
Lo siguiente que debe verificar es cuántos factores usar (o “extraer” de los datos). Hay tres enfoques diferentes disponibles:
Una convención es elegir todos los componentes con valores propios mayores que 12 . Esto nos daría cuatro factores con nuestros datos (pruébalo y verás).
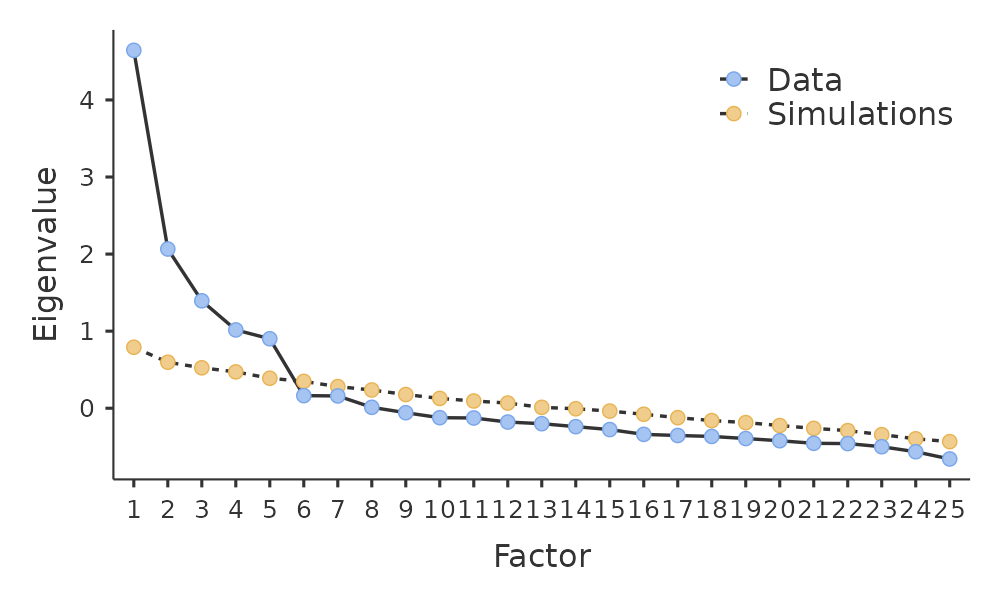
El examen del diagrama de pantalla, como en Figure 15.5, le permite identificar el “punto de inflexión”. Este es el punto en el que la pendiente de la curva del pedregal se nivela claramente, por debajo del “codo”. Esto nos daría cinco factores con nuestros datos. Interpretar scree plots es un poco un arte: en Figure 15.5 hay un paso notable de \(5\) a \(6\) factores, pero en otros scree plots que mire no será tan claro.
Mediante una técnica de análisis en paralelo, los valores propios obtenidos se comparan con los que se obtendrían a partir de datos aleatorios. El número de factores extraídos es el número con valores propios mayores que los que se encontrarían con datos aleatorios.
El tercer enfoque es bueno según Fabrigar et al. (1999), aunque en la práctica los investigadores tienden a observar los tres y luego emitir un juicio sobre la cantidad de factores que se interpretan de manera más fácil o útil. Esto puede entenderse como el “criterio de significado”, y los investigadores normalmente examinarán, además de la solución de uno de los enfoques anteriores, soluciones con uno o dos factores más o menos. Luego adoptan la solución que tiene más sentido para ellos.
Al mismo tiempo, también debemos considerar la mejor manera de rotar la solución final. Hay dos enfoques principales para la rotación: la rotación ortogonal (p. ej., ‘varimax’) obliga a que los factores seleccionados no estén correlacionados, mientras que la rotación oblicua (p. ej., ‘oblimin’) permite correlacionar los factores seleccionados. Las dimensiones de interés para los psicólogos y los científicos del comportamiento a menudo no son dimensiones que esperaríamos que fueran ortogonales, por lo que las soluciones oblicuas son posiblemente más sensatas2

Prácticamente, si en una rotación oblicua se encuentra que los factores están sustancialmente correlacionados (positivo o negativo, y > 0.3), como en Figure 15.6 donde una correlación entre dos de los factores extraídos es 0.31, entonces esto confirmaría nuestra intuición para preferir la rotación oblicua. Si los factores están, de hecho, correlacionados, entonces una rotación oblicua producirá una mejor estimación de los verdaderos factores y una mejor estructura simple que una rotación ortogonal. Y, si la rotación oblicua indica que los factores tienen correlaciones cercanas a cero entre sí, entonces el investigador puede continuar y realizar una rotación ortogonal (que luego debería dar aproximadamente la misma solución que la rotación oblicua).
Al comprobar la correlación entre los factores extraídos, al menos una correlación fue superior a 0,3 (Figure 15.6), por lo que se prefiere una rotación oblicua (“oblimin”) de los cinco factores extraídos. También podemos ver en Figure 15.6 que la proporción de la variación general en los datos que se explica por los cinco factores es del 46 %. El factor uno representa alrededor del 10% de la varianza, los factores dos a cuatro alrededor del 9% cada uno y el factor cinco un poco más del 7%. Esto no es genial; Hubiera sido mejor si la solución general explicara una proporción más sustancial de la varianza en nuestros datos.
Tenga en cuenta que en cada EFA podría tener potencialmente la misma cantidad de factores que variables observadas, pero cada factor adicional que incluya agregará una cantidad menor de varianza explicada. Si los primeros factores explican una buena cantidad de la varianza en las 25 variables originales, entonces esos factores son claramente un sustituto útil y más simple para las 25 variables. Puede eliminar el resto sin perder demasiado de la variabilidad original. Pero si se necesitan 18 factores (por ejemplo) para explicar la mayor parte de la variación en esas 25 variables, también podría usar los 25 originales.
Figure 15.7 muestra las cargas factoriales. Es decir, cómo se cargan los 25 elementos de personalidad diferentes en cada uno de los cinco factores seleccionados. Tenemos cargas ocultas menores a \(0.3\) (configuradas en las opciones que se muestran en Figure 15.3.
Para los Factores \(1, 2, 3\) y \(4\), el patrón de las cargas factoriales coincide estrechamente con los factores putativos especificados en Figure 15.2. ¡Uf! Y el factor \(5\) está bastante cerca, con cuatro de las cinco variables observadas que supuestamente miden la “apertura” cargando bastante bien en el factor. Sin embargo, la variable \(04\) no parece encajar, ya que la solución factorial en Figure 15.7 sugiere que se carga en el factor \(4\) (aunque con una carga relativamente baja) pero no sustancialmente en el factor \(5\).
La otra cosa a tener en cuenta es que aquellas variables que se denotaron como “R: codificación inversa” en Figure 15.2 son aquellas que tienen cargas de factores negativas. Eche un vistazo a los ítems A1 (“Soy indiferente a los sentimientos de los demás”) y A2 (“Pregunto por el bienestar de los demás”). Podemos ver que una puntuación alta en \(A1\) indica baja simpatía, mientras que una puntuación alta en \(A2\) (y todas las demás variables “A” para el caso) indica alta simpatía. Por lo tanto, A1 se correlacionará negativamente con las otras variables “A”, y es por eso que tiene una carga factorial negativa, como se muestra en Figure 15.7.
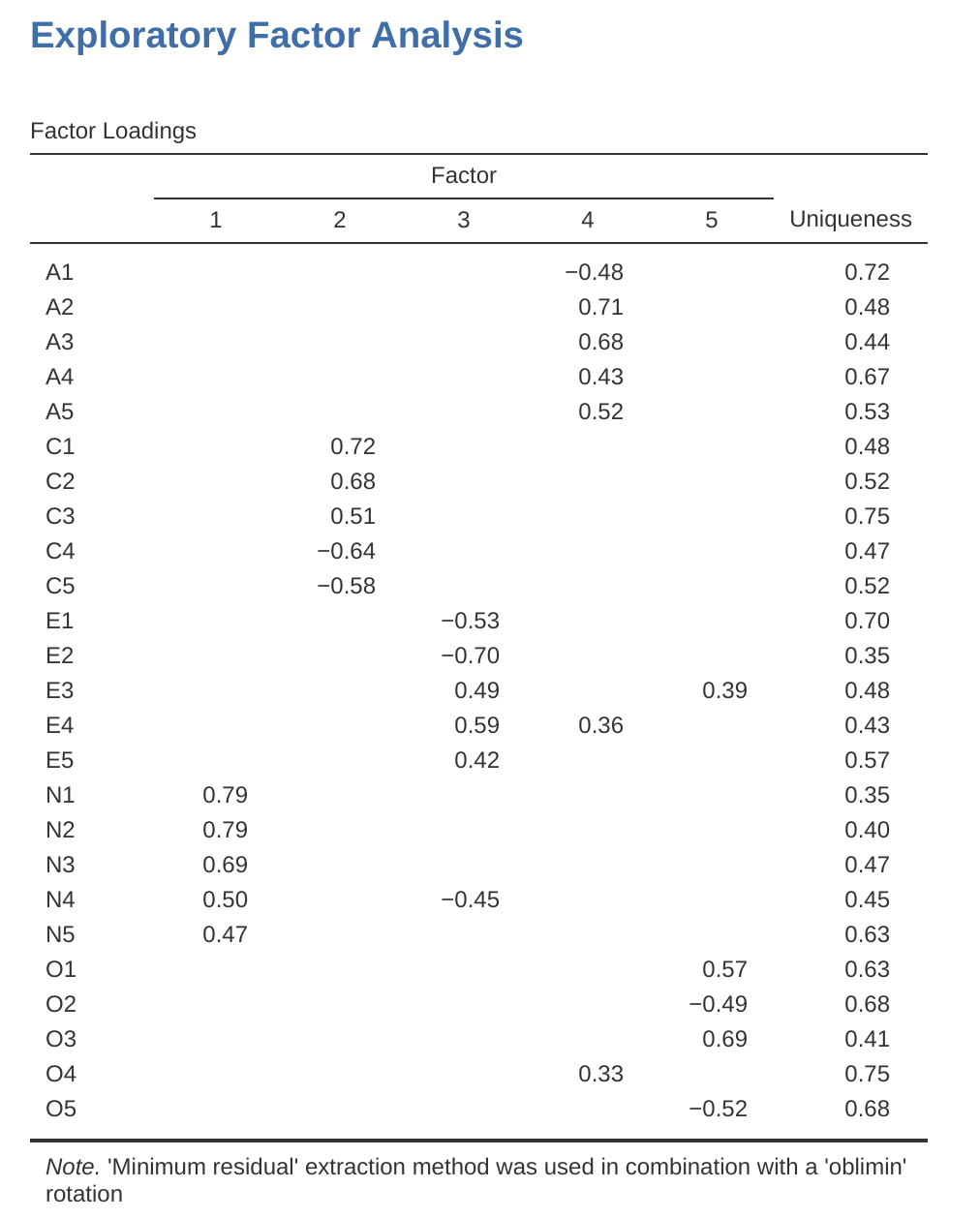
También podemos ver en Figure 15.7 la “singularidad” de cada variable. La singularidad es la proporción de varianza que es ‘única’ para la variable y no explicada por los factores3. Por ejemplo, el 72% de la varianza en ‘A1’ no se explica por los factores de la solución de cinco factores. Por el contrario, ‘N1’ tiene una varianza relativamente baja que no se explica en la solución factorial (35 %). Nótese que cuanto mayor es la ‘singularidad’, menor es la relevancia o contribución de la variable en el modelo factorial.
Para ser honesto, es inusual obtener una solución tan clara en EPT. Por lo general, es un poco más complicado que esto y, a menudo, interpretar el significado de los factores es más desafiante. No es frecuente que tenga un grupo de artículos tan claramente delineado. Más a menudo, tendrá un montón de variables observadas que cree que pueden ser indicadores de algunos factores latentes subyacentes, ¡pero no tiene un sentido tan fuerte de qué variables van a ir a dónde!
Por lo tanto, parece que tenemos una solución de cinco factores bastante buena, aunque representa una proporción general relativamente baja de la varianza observada. Supongamos que estamos contentos con esta solución y queremos usar nuestros factores en análisis posteriores. La opción sencilla es calcular una puntuación general (promedio) para cada factor sumando la puntuación de cada variable que se carga sustancialmente en el factor y luego dividiendo por el número de variables (en otras palabras, crear una “puntuación media” para cada persona a través de los ítems para cada escala Para cada persona en nuestro conjunto de datos que implica, por ejemplo, para el factor de Amabilidad, sumando \(A1 + A2 + A3 + A4 + A5\), y luego dividiendo por 5. 4 En esencia, el puntaje factorial que hemos calculado se basa en puntajes igualmente ponderados de cada una de las variables/ítems incluidos. Podemos hacer esto en jamovi en dos pasos:
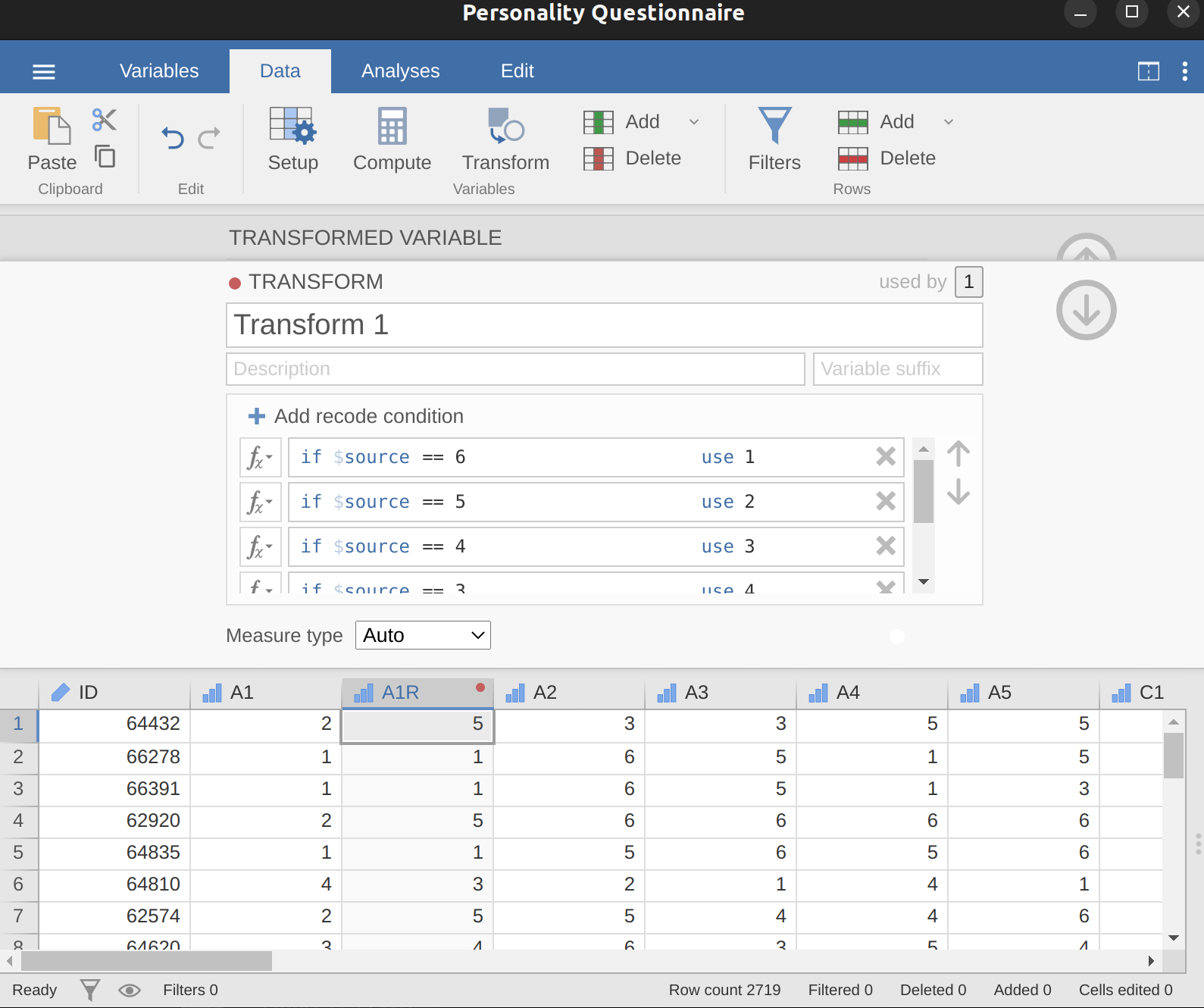
Recodifique A1 en “A1R” al revertir la puntuación de los valores en la variable (es decir, \(6 = 1\); \(5 = 2\); \(4 = 3\); \(3 = 4\); \(2 = 5\); \(1 = 6\)) usando el jamovi comando transform variable (ver Figure 15.8).
Calcule una nueva variable, llamada “Agradabilidad”, calculando la media de A1R, A2, A3, A4 y A5. Hágalo con el comando jamovi compute new variable (ver Figure 15.9).

Otra opción es crear un índice de puntaje factorial ** ponderado de manera óptima **. Para hacer esto, guarde las puntuaciones de los factores en el conjunto de datos, usando la casilla de verificación ‘Guardar’ - ‘Puntuaciones de los factores’. Una vez hecho esto verás que se han añadido cinco nuevas variables (columnas) a los datos, una por cada factor extraído. Ver Figure 15.10 y Figure 15.11.
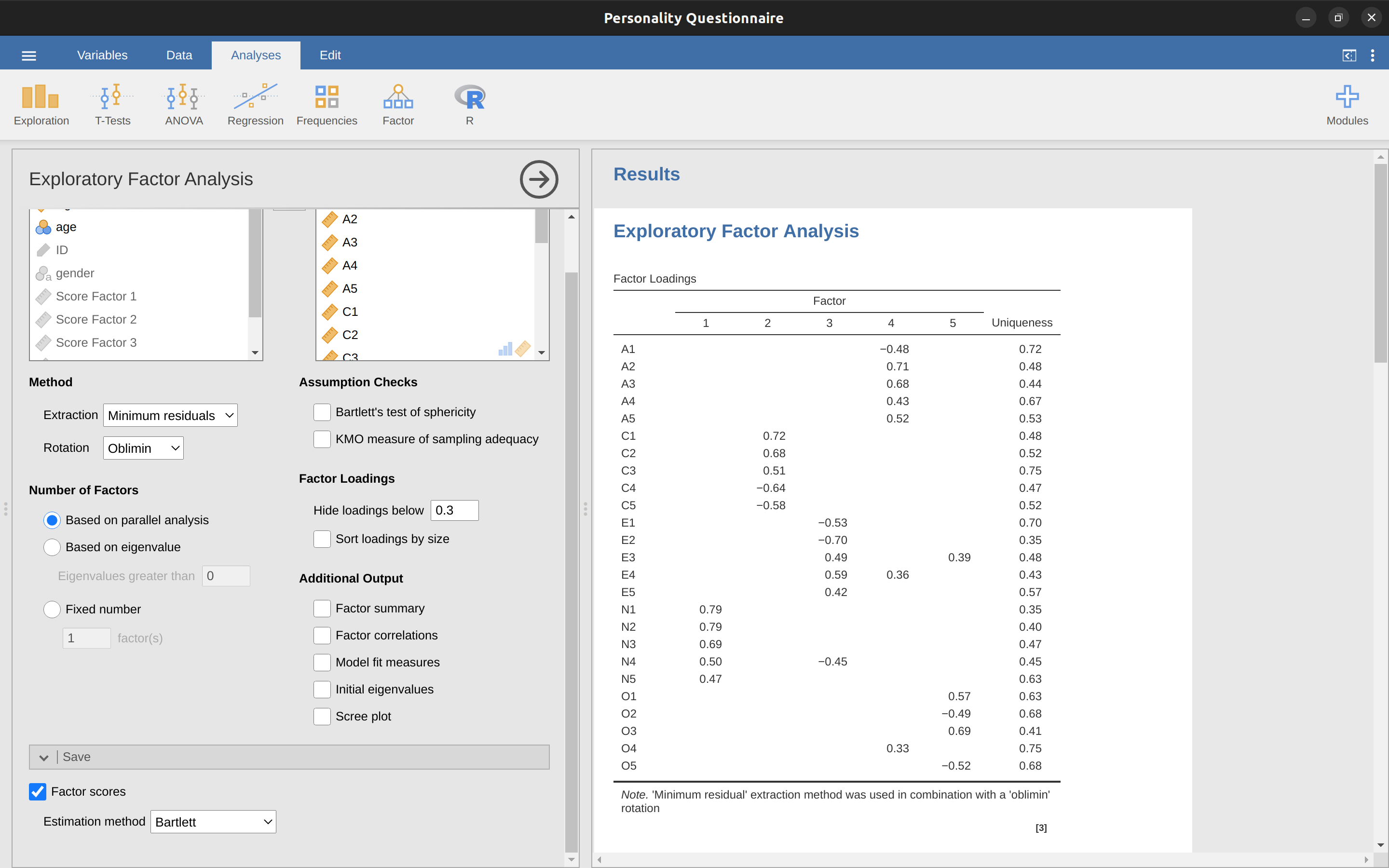
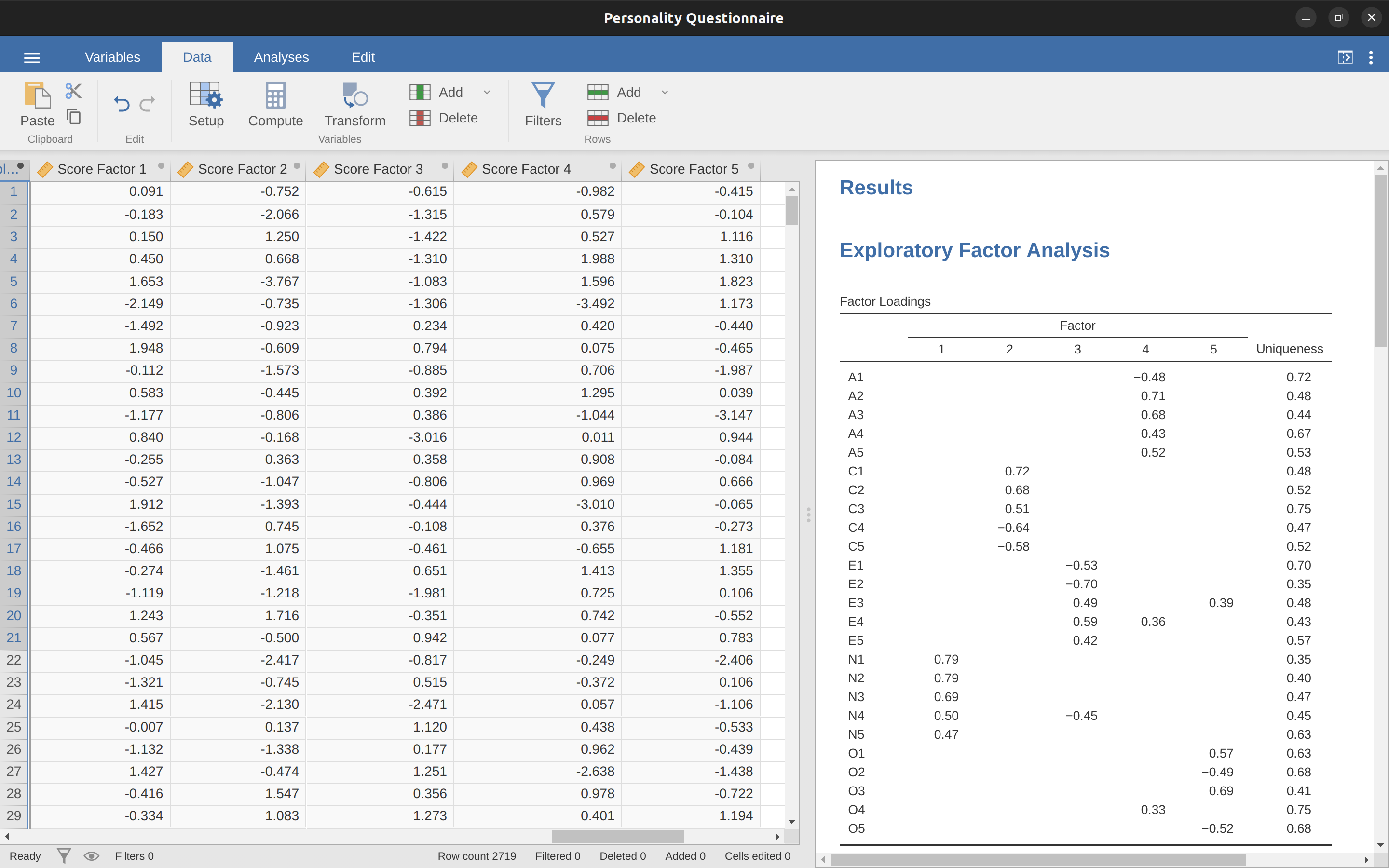
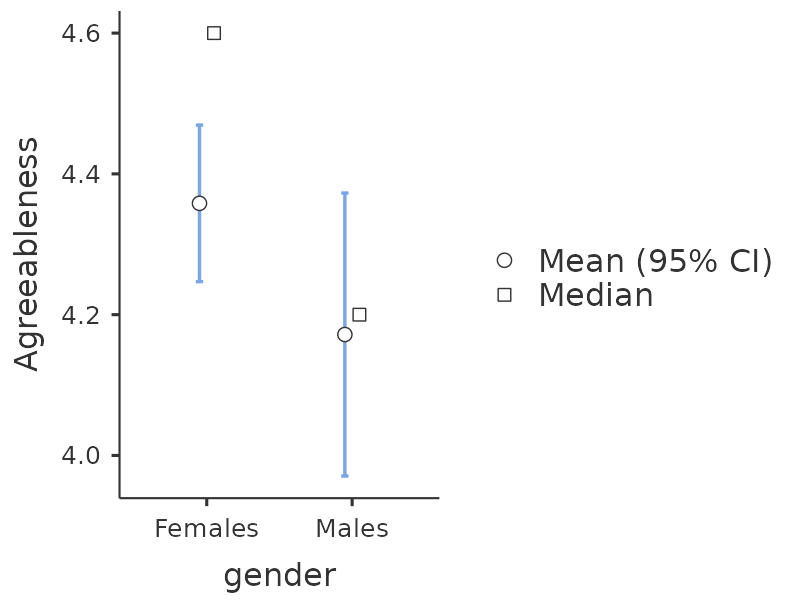
Ahora puede continuar y realizar más análisis, utilizando las escalas factoriales basadas en la puntuación media (p. ej., como en Figure 15.9) o utilizando las puntuaciones factoriales ponderadas de forma óptima calculadas por jamovi. ¡Tu elección! Por ejemplo, una cosa que le gustaría hacer es ver si hay diferencias de género en cada una de nuestras escalas de personalidad. Hicimos esto para la puntuación de Amabilidad que calculamos utilizando el enfoque de puntuación media, y aunque la gráfica de la prueba t (Figure 15.12) mostró que los hombres eran menos agradables que las mujeres, esto no fue una diferencia significativa (Mann-Whitney $ U = 5768$, \(p = .075\)).
15.1.4 Escribir un EFA
Con suerte, hasta ahora le hemos dado una idea de la EPT y cómo llevar a cabo la EPT en jamovi. Entonces, una vez que haya completado su EFA, ¿cómo lo escribe? No existe una forma estándar formal de redactar una EFA, y los ejemplos tienden a variar según la disciplina y el investigador. Dicho esto, hay algunas piezas de información bastante estándar para incluir en su redacción:
¿Cuáles son los fundamentos teóricos para el área que está estudiando, y específicamente para los constructos que le interesa descubrir a través de EPT?
Una descripción de la muestra (por ejemplo, información demográfica, tamaño de la muestra, método de muestreo).
Una descripción del tipo de datos utilizados (p. ej., nominales, continuos) y estadísticas descriptivas.
Describa cómo hizo para probar los supuestos de la EFA. Se deben informar los detalles sobre los controles de esfericidad y las medidas de adecuación del muestreo.
Explique qué método de extracción de FA (p. ej., ‘Residuos mínimos’ o ‘Máxima probabilidad’) se utilizó.
Explique los criterios y el proceso utilizado para decidir cuántos factores se extrajeron en la solución final y qué elementos se seleccionaron. Explique claramente la justificación de las decisiones clave durante el proceso de EFA.
Explique qué métodos de rotación se intentaron, los motivos y los resultados.
Las cargas factoriales finales deben informarse en los resultados, en una tabla. Esta tabla también debe informar la singularidad (o comunalidad) de cada variable (en la última columna). Las cargas factoriales deben informarse con etiquetas descriptivas además de los números de artículo. Las correlaciones entre los factores también deben incluirse, ya sea en la parte inferior de esta tabla, en una tabla separada.
Deben proporcionarse nombres significativos para los factores extraídos. Es posible que desee utilizar nombres de factores previamente seleccionados, pero al examinar los elementos y factores reales, puede pensar que un nombre diferente es más apropiado.
15.2 Análisis de componentes principales
En la sección anterior vimos que EPT trabaja para identificar factores latentes subyacentes. Y, como vimos, en un escenario, el número más pequeño de factores latentes se puede usar en análisis estadísticos adicionales usando algún tipo de puntajes de factores combinados.
De esta manera, EFA se está utilizando como una técnica de “reducción de datos”. Otro tipo de técnica de reducción de datos, a veces vista como parte de la familia EFA, es el análisis de componentes principales (PCA). Sin embargo, PCA no identifica factores latentes subyacentes. En su lugar, crea una puntuación compuesta lineal a partir de un conjunto más grande de variables medidas.
PCA simplemente produce una transformación matemática a los datos originales sin suposiciones sobre cómo las variables co-varían. El objetivo de PCA es calcular algunas combinaciones lineales (componentes) de las variables originales que se pueden usar para resumir el conjunto de datos observados sin perder mucha información. Sin embargo, si la identificación de la estructura subyacente es un objetivo del análisis, entonces se prefiere EFA. Y, como vimos, EFA produce puntajes factoriales que se pueden usar para propósitos de reducción de datos al igual que los puntajes de componentes principales (Fabrigar et al., 1999).
PCA ha sido popular en psicología por varias razones y, por lo tanto, vale la pena mencionarlo, aunque hoy en día EFA es tan fácil de hacer dada la potencia de las computadoras de escritorio y puede ser menos susceptible al sesgo que PCA, especialmente con una pequeña cantidad de factores. y variables. Gran parte del procedimiento es similar a EFA, por lo que, aunque existen algunas diferencias conceptuales, prácticamente los pasos son los mismos, y con muestras grandes y un número suficiente de factores y variables, los resultados de PCA y EFA deberían ser bastante similares.
Para realizar PCA en jamovi, todo lo que necesita hacer es seleccionar ‘Factor’ - ‘Análisis de componentes principales’ en la barra de botones principal de jamovi para abrir la ventana de análisis de PCA. Luego puede seguir los mismos pasos de [EFA en jamovi] arriba.
15.3 Análisis factorial confirmatorio
Por lo tanto, nuestro intento de identificar los factores latentes subyacentes utilizando EFA con preguntas cuidadosamente seleccionadas del conjunto de elementos de personalidad pareció tener bastante éxito. El próximo paso en nuestra búsqueda para desarrollar una medida útil de la personalidad es verificar los factores latentes que identificamos en el EFA original con una muestra diferente. Queremos ver si los factores se mantienen, si podemos confirmar su existencia con datos diferentes. Esta es una verificación más rigurosa, como veremos. Y se llama Análisis factorial confirmatorio (CFA) ya que, como era de esperar, buscaremos confirmar una estructura de factor latente especificada previamente.5
En CFA, en lugar de hacer un análisis en el que vemos cómo los datos van juntos en un sentido exploratorio, imponemos una estructura, como en Figure 15.13, sobre los datos y vemos qué tan bien se ajustan a nuestros datos preespecificados. estructura. En este sentido, estamos realizando un análisis confirmatorio, para ver qué tan bien los datos observados confirman un modelo preespecificado.
Por lo tanto, un análisis factorial confirmatorio (CFA) directo de los ítems de personalidad especificaría cinco factores latentes como se muestra en Figure 15.13, cada uno medido por cinco variables observadas. Cada variable es una medida de un factor latente subyacente. Por ejemplo, A1 se predice por el factor latente subyacente Amabilidad. Y debido a que A1 no es una medida perfecta del factor de simpatía, hay un término de error, \(e\), asociado con él. En otras palabras, \(e\) representa la variación en A1 que no se explica por el factor de simpatía. Esto a veces se denomina error de medición.

El siguiente paso es considerar si se debe permitir que los factores latentes se correlacionen en nuestro modelo. Como se mencionó anteriormente, en las ciencias psicológicas y del comportamiento, los constructos a menudo están relacionados entre sí, y también pensamos que algunos de nuestros factores de personalidad pueden estar correlacionados entre sí. Entonces, en nuestro modelo, deberíamos permitir que estos factores latentes covaríen, como lo muestran las flechas de dos puntas en Figure 15.13.
Al mismo tiempo, debemos considerar si existe alguna buena razón sistemática para que algunos de los términos de error estén correlacionados entre sí. Una razón para esto podría ser que existe una característica metodológica compartida para subconjuntos particulares de las variables observadas, de modo que las variables observadas pueden estar correlacionadas por razones metodológicas en lugar de factores latentes sustantivos. Volveremos a esta posibilidad en una sección posterior pero, por ahora, no hay razones claras que podamos ver que justifiquen correlacionar algunos de los términos de error entre sí.
Sin ningún término de error correlacionado, el modelo que estamos probando para ver qué tan bien se ajusta a nuestros datos observados es tal como se especifica en Figure 15.13. Solo se espera encontrar en los datos los parámetros que están incluidos en el modelo, por lo que en CFA todos los demás parámetros posibles (coeficientes) se establecen en cero. Entonces, si estos otros parámetros no son cero (por ejemplo, puede haber una carga sustancial de A1 en el factor latente Extraversión en los datos observados, pero no en nuestro modelo), entonces podemos encontrar un ajuste deficiente entre nuestro modelo y los datos observados. .
Correcto, echemos un vistazo a cómo configuramos este análisis CFA en jamovi.
15.3.1 CFA en Jamovi
Abra el archivo bfi_sample2.csv, verifique que las 25 variables estén codificadas como ordinales (o continuas; no supondrá ninguna diferencia para este análisis). Para realizar CFA en jamovi:
Seleccione Factor - Análisis factorial confirmatorio en la barra de botones principal de jamovi para abrir la ventana de análisis CFA (Figure 15.14).
Seleccione las variables 5 A y transfiéralas al cuadro ‘Factores’ y asígnele la etiqueta “Agradabilidad”.
Cree un nuevo Factor en el cuadro ‘Factores’ y etiquételo como “Conciencia”. Seleccione las 5 variables C y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Consciencia”.
Cree otro Factor nuevo en el cuadro ‘Factores’ y etiquételo como “Extraversión”. Seleccione las 5 variables E y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Extraversión”.
Cree otro Factor nuevo en el cuadro ‘Factores’ y etiquételo como “Neuroticismo”. Seleccione las 5 N variables y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Neuroticismo”.
Cree otro Factor nuevo en el cuadro ‘Factores’ y etiquételo como “Apertura”. Seleccione las 5 variables O y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Apertura”.
Verifique otras opciones apropiadas, los valores predeterminados están bien para este trabajo inicial, aunque es posible que desee verificar la opción “Diagrama de ruta” en “Gráficos” para ver que jamovi produce un diagrama (bastante) similar a nuestro Figure 15.13 .
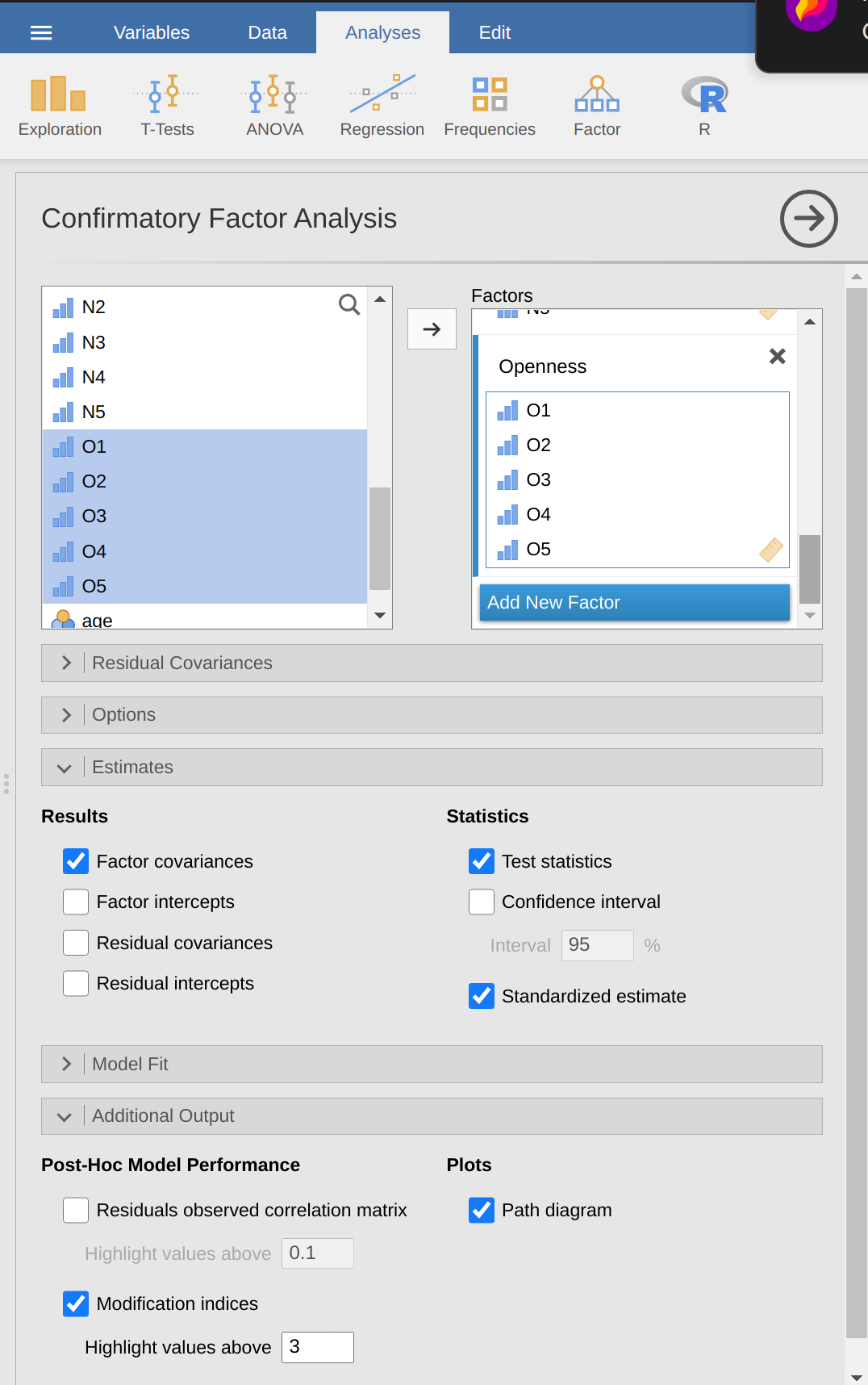
Una vez que hayamos configurado el análisis, podemos dirigir nuestra atención a la ventana de resultados de jamovi y ver qué es qué. Lo primero que hay que mirar es el ajuste del modelo (Figure 15.15), ya que nos dice qué tan bien se ajusta nuestro modelo a los datos observados. NB en nuestro modelo solo se estiman las covarianzas preespecificadas, incluidas las correlaciones de factores por defecto. Todo lo demás se pone a cero.
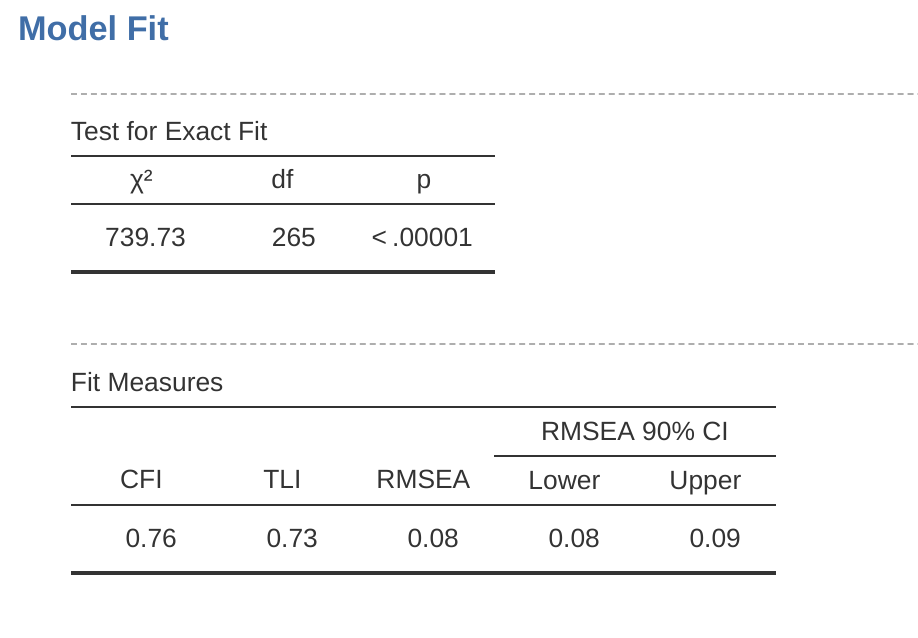
Hay varias formas de evaluar el ajuste del modelo. La primera es una estadística de chi-cuadrado que, si es pequeña, indica que el modelo se ajusta bien a los datos. Sin embargo, la estadística de chi-cuadrado utilizada para evaluar el ajuste del modelo es bastante sensible al tamaño de la muestra, lo que significa que con una muestra grande, un ajuste lo suficientemente bueno entre el modelo y los datos casi siempre produce un chi grande y significativo (p < .05). valor cuadrado.
Por lo tanto, necesitamos otras formas de evaluar el ajuste del modelo. En jamovi se proporcionan varios por defecto. Estos son el índice de ajuste comparativo (CFI), el índice de Tucker Lewis (TLI) y el error cuadrático medio de aproximación (RMSEA) junto con el intervalo de confianza del 90 % para el RMSEA. Algunas reglas generales útiles son que un ajuste satisfactorio está indicado por CFI > 0,9, TLI > 0,9 y RMSEA de aproximadamente 0,05 a 0,08. Un buen ajuste es CFI > 0,95, TLI > 0,95 y RMSEA y CI superior para RMSEA < 0,05.
Entonces, mirando Figure 15.15 podemos ver que el valor de chi-cuadrado es grande y altamente significativo. Nuestro tamaño de muestra no es demasiado grande, por lo que esto posiblemente indica un mal ajuste. El CFI es de \(0.762\) y el TLI es de 0.731, lo que indica un mal ajuste entre el modelo y los datos. El RMSEA es de \(0.085\) con un intervalo de confianza de \(90\%\) de \(0.077\) a \(0.092\), de nuevo esto no indica un buen ajuste.
Bastante decepcionante, ¿eh? Pero tal vez no sea demasiado sorprendente dado que en el EFA anterior, cuando ejecutamos con un conjunto de datos similar (consulte la sección Análisis factorial exploratorio), solo alrededor de la mitad de la varianza en los datos fue explicada por el modelo de cinco factores.
Pasemos a ver las cargas factoriales y las estimaciones de la covarianza factorial, que se muestran en Figure 15.16 y Figure 15.17. La estadística Z y el valor p para cada uno de estos parámetros indican que hacen una contribución razonable al modelo (es decir, no son cero), por lo que no parece haber ninguna razón para eliminar ninguna de las rutas de factores variables especificadas. o correlaciones factor-factor del modelo. A menudo, las estimaciones estandarizadas son más fáciles de interpretar y se pueden especificar en la opción ‘Estimaciones’. Estas tablas pueden incorporarse de manera útil en un informe escrito o artículo científico.
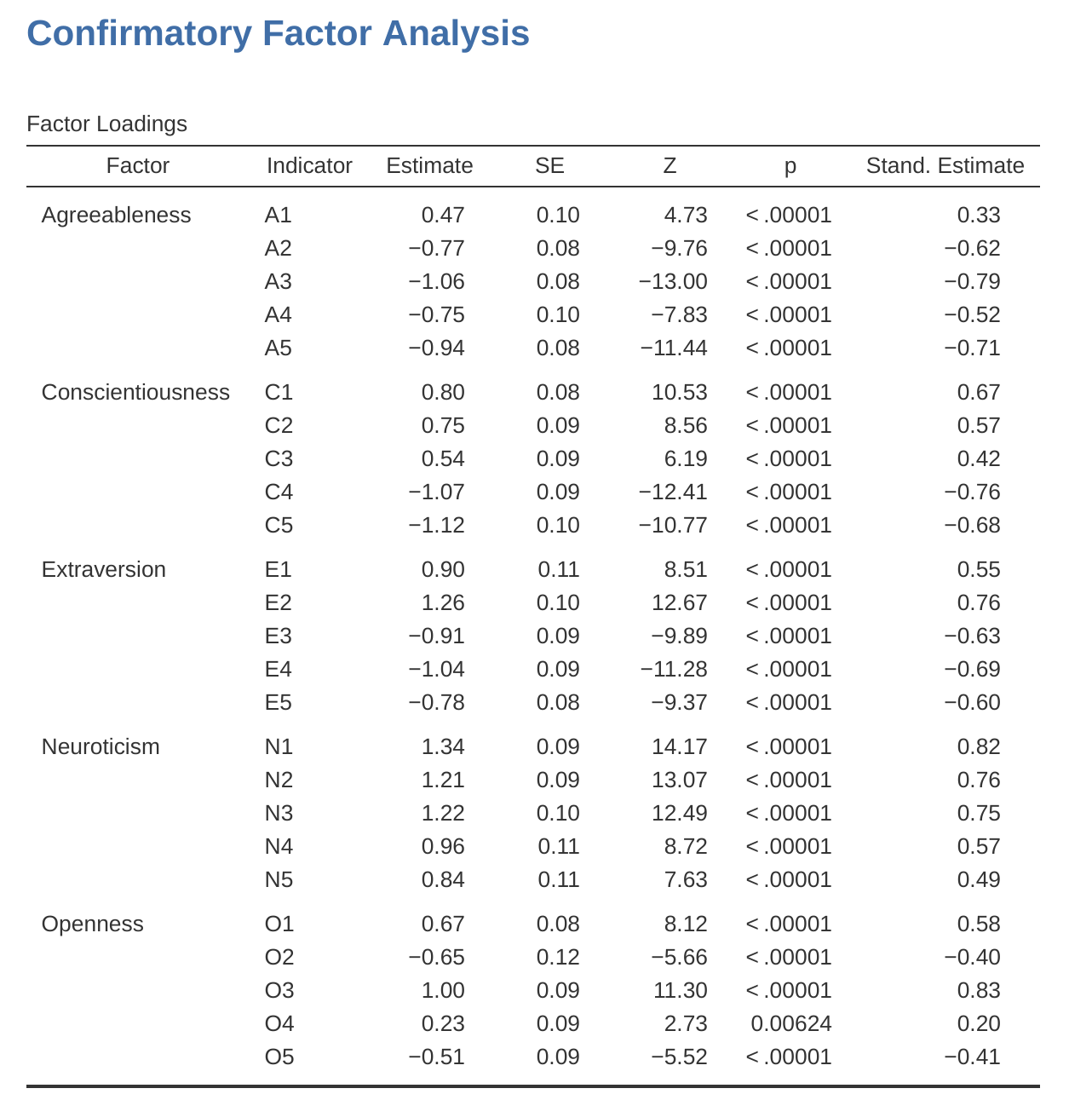
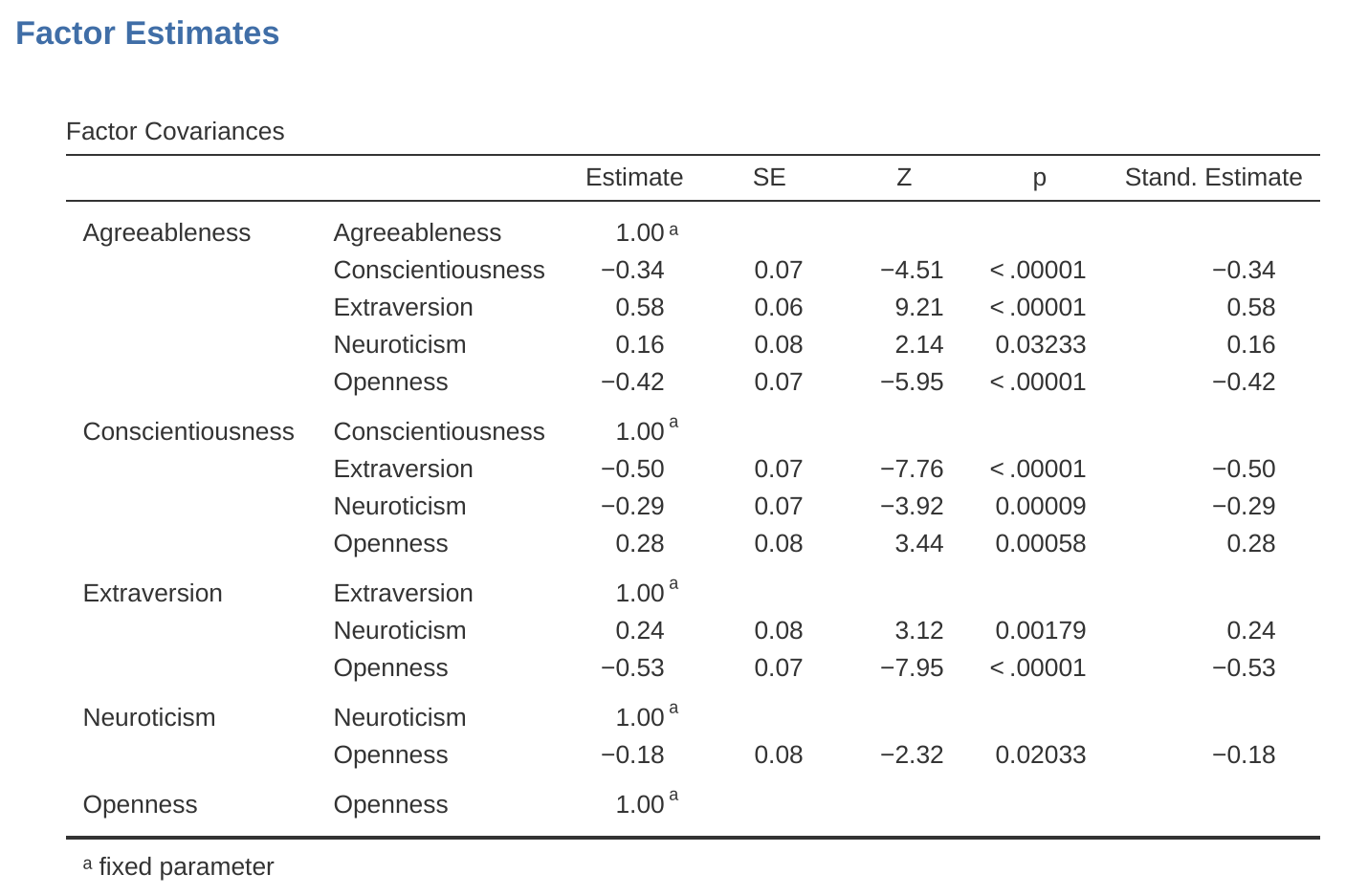
¿Cómo podríamos mejorar el modelo? Una opción es retroceder algunas etapas y volver a pensar en los elementos/medidas que estamos usando y cómo podrían mejorarse o cambiarse. Otra opción es hacer algunos ajustes post hoc al modelo para mejorar el ajuste. Una forma de hacerlo es usar “índices de modificación” (Figure 15.18), especificados como una opción de “Salida adicional” en jamovi.
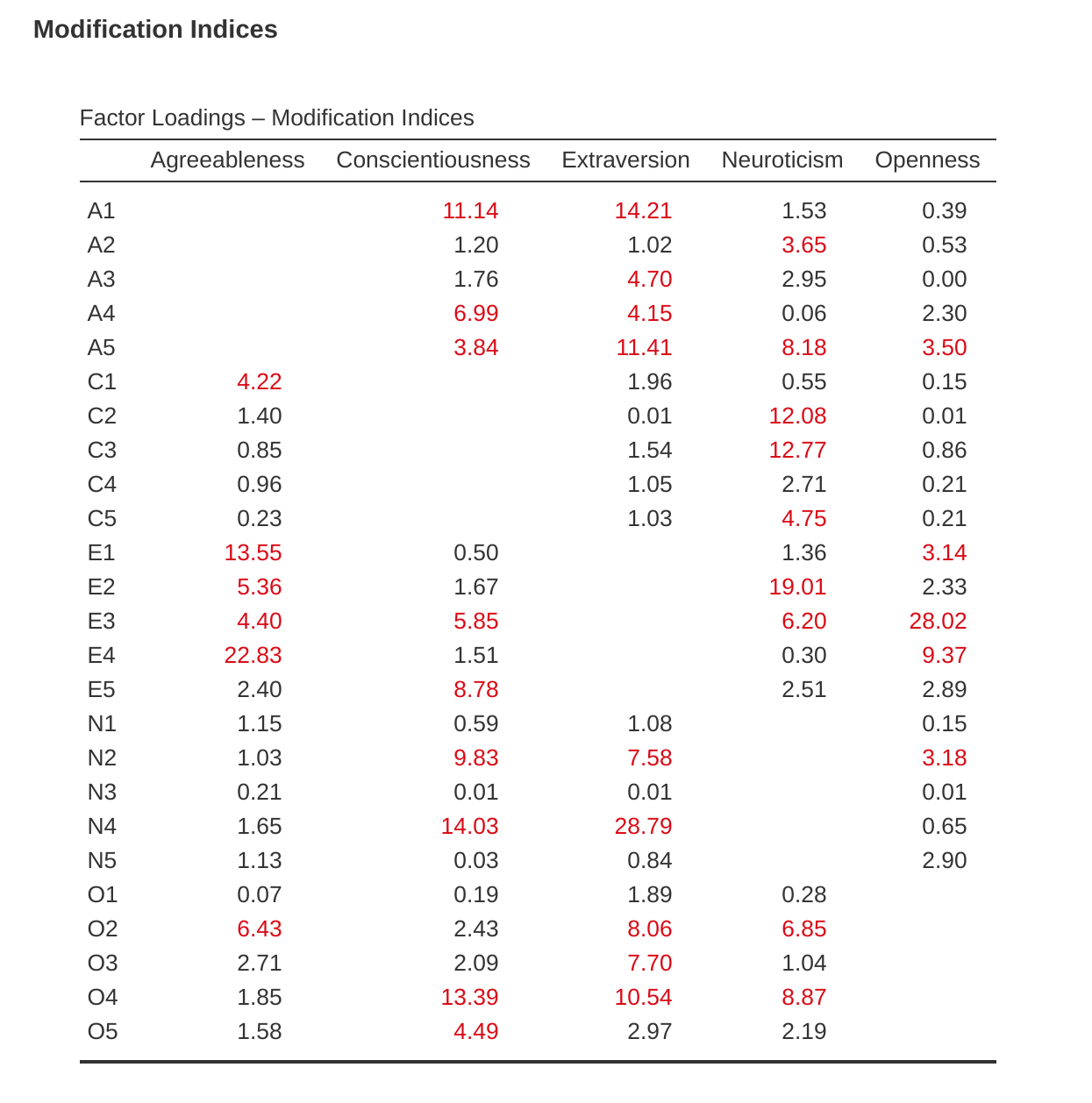
Lo que estamos buscando es el valor más alto del índice de modificación (MI). Luego juzgaríamos si tiene sentido agregar ese término adicional al modelo, usando una racionalización post hoc. Por ejemplo, podemos ver en Figure 15.18 que el MI más grande para las cargas factoriales que aún no están en el modelo es un valor de 28.786 para la carga de N4 (“A menudo se siente triste”) en el factor latente Extraversión . Esto indica que si agregamos esta ruta al modelo, el valor de chi-cuadrado se reducirá aproximadamente en la misma cantidad.
Pero en nuestro modelo, podría decirse que agregar este camino realmente no tiene ningún sentido teórico o metodológico, por lo que no es una buena idea (a menos que pueda presentar un argumento persuasivo de que “A menudo me siento triste” mide tanto el neuroticismo como la extraversión). No puedo pensar en una buena razón. Pero, por el bien del argumento, supongamos que tiene algún sentido y agreguemos este camino al modelo. Vuelva a la ventana de análisis CFA (consulte Figure 15.14) y agregue N4 al factor de extraversión. Los resultados del CFA ahora cambiarán (no se muestra); el chi-cuadrado se ha reducido a alrededor de 709 (una caída de alrededor de 30, aproximadamente similar al tamaño del MI) y los otros índices de ajuste también han mejorado, aunque solo un poco. Pero no es suficiente: todavía no es un buen modelo de ajuste.
Si se encuentra agregando nuevos parámetros a un modelo utilizando los valores de MI, siempre vuelva a verificar las tablas de MI después de cada nueva adición, ya que los MI se actualizan cada vez.
También hay una tabla de índices de modificación de covarianza residual producida por jamovi (Figure 15.19). En otras palabras, una tabla que muestre qué errores correlacionados, si se agregan al modelo, mejorarían más el ajuste del modelo. Es una buena idea mirar ambas tablas de MI al mismo tiempo, detectar el MI más grande, pensar si la adición del parámetro sugerido puede justificarse razonablemente y, si es posible, agregarlo al modelo. Y luego puede comenzar nuevamente a buscar el MI más grande en los resultados recalculados.

Puede seguir así todo el tiempo que desee, agregando parámetros al modelo en función del MI más grande y, finalmente, logrará un ajuste satisfactorio. ¡Pero también habrá una gran posibilidad de que al hacer esto hayas creado un monstruo! Un modelo feo y deforme que no tiene ningún sentido teórico ni pureza. En otras palabras, ¡ten mucho cuidado!
Hasta ahora hemos comprobado la estructura factorial obtenida en el AFE utilizando una segunda muestra y AFC. Desafortunadamente, no encontramos que la estructura factorial del EFA se confirmara en el CFA, por lo que está de vuelta en el tablero de dibujo en lo que respecta al desarrollo de esta escala de personalidad.
Aunque podríamos haber ajustado el CFA usando índices de modificación, realmente no había ninguna buena razón (que se me ocurriera) para incluir estas cargas factoriales adicionales sugeridas o covarianzas residuales. Sin embargo, a veces hay una buena razón para permitir que los residuos covaríen (o se correlacionen), y un buen ejemplo de esto se muestra en la siguiente sección sobre [CFA de múltiples características y múltiples métodos]. Antes de hacer eso, veamos cómo informar los resultados de un CFA.
15.3.2 Reportar un CFA
No existe una forma estándar formal de redactar un CFA, y los ejemplos tienden a variar según la disciplina y el investigador. Dicho esto, hay algunas piezas de información bastante estándar para incluir en su redacción:
Una justificación teórica y empírica del modelo hipotético.
Una descripción completa de cómo se especificó el modelo (p. ej., las variables indicadoras para cada factor latente, las covarianzas entre las variables latentes y cualquier correlación entre los términos de error). Sería bueno incluir un diagrama de ruta, como el de Figure 15.13.
Una descripción de la muestra (por ejemplo, información demográfica, tamaño de la muestra, método de muestreo).
Una descripción del tipo de datos utilizados (p. ej., nominales, continuos) y estadísticas descriptivas.
Pruebas de supuestos y método de estimación utilizado.
Una descripción de los datos faltantes y cómo se manejaron los datos faltantes.
El software y la versión utilizados para adaptarse al modelo.
Medidas y criterios utilizados para juzgar el ajuste del modelo.
Cualquier alteración realizada en el modelo original en función de los índices de ajuste o modificación del modelo.
Todas las estimaciones de parámetros (es decir, cargas, varianzas de error, (co)varianzas latentes) y sus errores estándar, probablemente en una tabla.
15.4 Múltiples Rasgos Múltiples Métodos CFA
En esta sección, consideraremos cómo las diferentes técnicas o preguntas de medición pueden ser una fuente importante de variabilidad de datos, conocida como varianza del método. Para hacer esto, usaremos otro conjunto de datos psicológicos, uno que contiene datos sobre el “estilo atribucional”.
Se utilizó el Cuestionario de Estilo Atribucional (ASQ) (Hewitt et al., 2004) para recopilar datos de bienestar psicológico de jóvenes en el Reino Unido y Nueva Zelanda. Midieron el estilo atribucional de los eventos negativos, que es la forma en que las personas suelen explicar la causa de las cosas malas que les suceden (Peterson & Seligman, 1984). El cuestionario de estilo atribucional (ASQ) mide tres aspectos del estilo atribucional:
La internalidad es el grado en que una persona cree que la causa de un mal evento se debe a sus propias acciones.
La estabilidad se refiere a la medida en que una persona cree habitualmente que la causa de un mal evento es estable a lo largo del tiempo.
La globalidad se refiere al grado en que una persona cree habitualmente que la causa de un mal evento en un área afectará otras áreas de su vida.
Hay seis escenarios hipotéticos y para cada escenario los encuestados responden una pregunta dirigida a (a) la interioridad, (b) la estabilidad y (c) la globalidad. Así que hay \(6 \times 3 = 18\) artículos en total. Consulte Figure 15.20 para obtener más detalles.

Los investigadores están interesados en verificar sus datos para ver si hay algunos factores latentes subyacentes que las 18 variables observadas en el ASQ miden razonablemente bien.
Primero, prueban EFA con estas 18 variables (no se muestran), pero no importa cómo extraigan o roten, no pueden encontrar una buena solución factorial. Su intento de identificar los factores latentes subyacentes en el Cuestionario de Estilo Atribucional (ASQ) resultó infructuoso. Si obtiene resultados como este, entonces su teoría es incorrecta (no hay una estructura de factores latentes subyacente para el estilo atribucional, lo cual es posible), la muestra no es relevante (lo cual es poco probable dado el tamaño y las características de esta muestra de adultos jóvenes de el Reino Unido y Nueva Zelanda), o el análisis no era la herramienta adecuada para el trabajo. Vamos a ver esta tercera posibilidad.
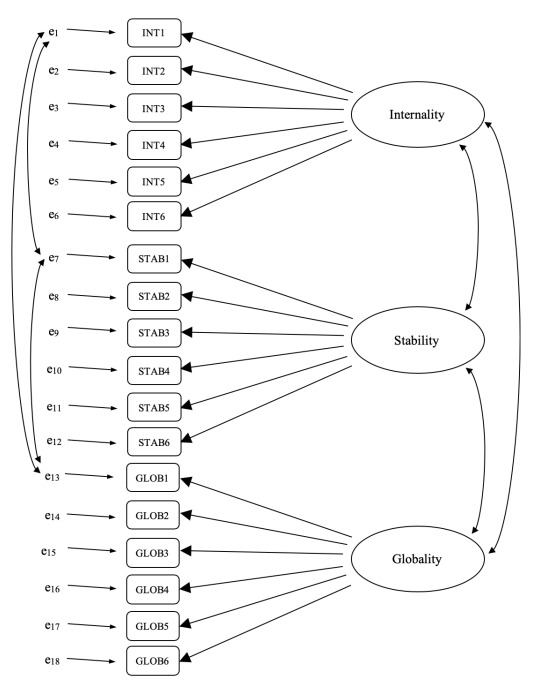
Recuerde que había tres dimensiones medidas en el ASQ: Internalidad, Estabilidad y Globalidad, cada una medida por seis preguntas como se muestra en Figure 15.21.
¿Qué pasa si, en lugar de hacer un análisis en el que vemos cómo los datos van juntos en un sentido exploratorio, imponemos una estructura, como en Figure 15.21, sobre los datos y vemos qué tan bien se ajustan a nuestros datos preespecificados? estructura. En este sentido, estamos realizando un análisis confirmatorio, para ver qué tan bien los datos observados confirman un modelo preespecificado.
Por lo tanto, un análisis factorial confirmatorio (CFA) directo del ASQ especificaría tres factores latentes, como se muestra en las columnas de Figure 15.27, cada uno medido por seis variables observadas.
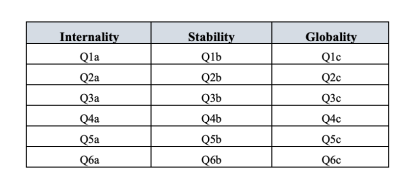
Podríamos representar esto como en el diagrama en Figure 15.22, que muestra que cada variable es una medida de un factor latente subyacente. Por ejemplo, INT1 se predice mediante el factor latente subyacente Internalidad. Y debido a que INT1 no es una medida perfecta del factor de internalidad, hay un término de error, e1, asociado con él. En otras palabras, e1 representa la varianza en INT1 que no se explica por el factor de Internalidad. Esto a veces se denomina “error de medición”.
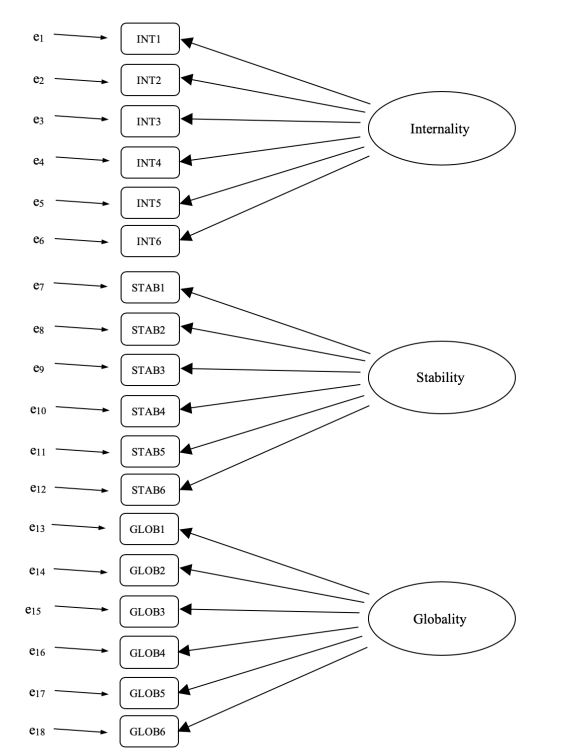
El siguiente paso es considerar si se debe permitir que los factores latentes se correlacionen en nuestro modelo. Como se mencionó anteriormente, en las ciencias psicológicas y del comportamiento, los constructos a menudo están relacionados entre sí, y también pensamos que la Internalidad, la Estabilidad y la Globalidad pueden estar correlacionadas entre sí, por lo que en nuestro modelo deberíamos permitir que estos factores latentes covaríen. , como se muestra en Figure 15.23.
Al mismo tiempo, debemos considerar si existe alguna buena razón sistemática para que algunos de los términos de error estén correlacionados entre sí. Volviendo a las preguntas del ASQ, había tres subpreguntas diferentes (a, byc) para cada pregunta principal (1-6). La P1 se refería a la búsqueda de empleo sin éxito y es plausible que esta pregunta tenga algunos aspectos metodológicos o artefactos distintivos además de las otras preguntas (2-5), quizás algo relacionado con la búsqueda de empleo. De manera similar, P2 se trataba de no ayudar a un amigo con un problema, y puede haber algunos aspectos metodológicos o de artefacto distintivos relacionados con no ayudar a un amigo que no están presentes en las otras preguntas (1 y 3-5).
Entonces, además de múltiples factores, también tenemos múltiples características metodológicas en el ASQ, donde cada una de las preguntas 1 a 6 tiene un “método” ligeramente diferente, pero cada “método” se comparte en las subpreguntas a, b y c. . Para incorporar estas diferentes características metodológicas en el modelo, podemos especificar que ciertos términos de error estén correlacionados entre sí. Por ejemplo, los errores asociados con INT1, STAB1 y GLOB1 deben correlacionarse entre sí para reflejar la varianza metodológica distinta y compartida de Q1a, Q1b y Q1c. Mirando Figure 15.21, esto significa que además de los factores latentes representados por las columnas, tendremos errores de medición correlacionados para las variables en cada fila de la tabla.
Si bien un modelo CFA básico como el que se muestra en Figure 15.22 podría probarse con nuestros datos observados, de hecho hemos creado un modelo más sofisticado, como se muestra en el diagrama en Figure 15.23. Este modelo CFA más sofisticado se conoce como modelo Multi-Trait Multi-Method (MTMM), y es el que probaremos en jamovi.
15.4.1 MTMM CFA en Jamovi
Abra el archivo ASQ.csv y compruebe que las 18 variables (seis variables de “Internalidad”, seis de “Estabilidad” y seis de “Globalidad”) se especifican como variables continuas.
Para realizar MTMM CFA en jamovi:
Seleccione Factor - Análisis factorial confirmatorio en la barra de botones principal de jamovi para abrir la ventana de análisis CFA (Figure 15.24).
Seleccione las 6 variables INT y transfiéralas al cuadro ‘Factores’ y asígneles la etiqueta “Internalidad”.
Cree un nuevo Factor en el cuadro ‘Factores’ y etiquételo como “Estabilidad”. Seleccione las 6 variables STAB y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Estabilidad”.
Cree otro Factor nuevo en el cuadro ‘Factores’ y etiquételo como “Globalidad”. Seleccione las 6 variables GLOB y transfiéralas al cuadro ‘Factores’ debajo de la etiqueta “Globalidad”.
Abra las opciones de Covarianzas residuales y, para cada una de nuestras correlaciones preespecificadas, mueva las variables asociadas al cuadro “Covarianzas residuales” de la derecha. Por ejemplo, resalte INT1 y STAB1 y luego haga clic en la flecha para moverlos. Ahora haga lo mismo para INT1 y GLOB1, para STAB1 y GLOB1, para INT2 y STAB2, para INT2 y GLOB2, para STAB2 y GLOB2, para INT3 y STAB3, y así sucesivamente.
Verifique otras opciones apropiadas, los valores predeterminados están bien para este trabajo inicial, aunque es posible que desee verificar la opción “Diagrama de ruta” en “Gráficos” para ver que jamovi produce un diagrama (bastante) similar a nuestro Figure 15.23 , e incluyendo todas las correlaciones de términos de error que hemos agregado anteriormente.
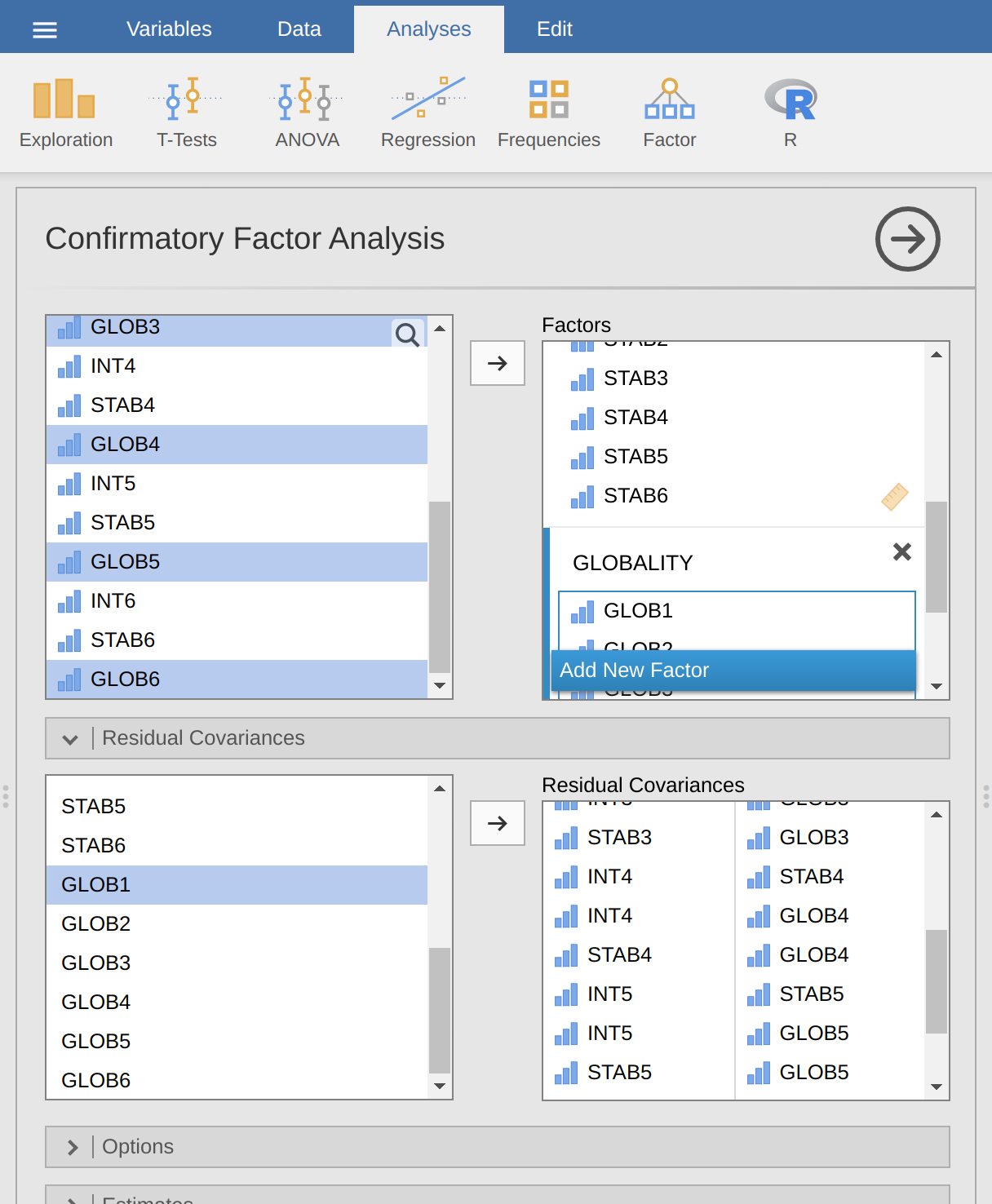
Una vez que hayamos configurado el análisis, podemos dirigir nuestra atención a la ventana de resultados de jamovi y ver qué es qué. Lo primero que debe observar es el “Ajuste del modelo”, ya que esto nos dice qué tan bien se ajusta nuestro modelo a los datos observados (Figure 15.25). NB en nuestro modelo solo se estiman las covarianzas preespecificadas, todo lo demás se establece en cero, por lo que el ajuste del modelo prueba si los parámetros “libres” preespecificados no son cero y, por el contrario, si las otras relaciones en los datos – los que no hemos especificado en el modelo, se pueden mantener en cero.
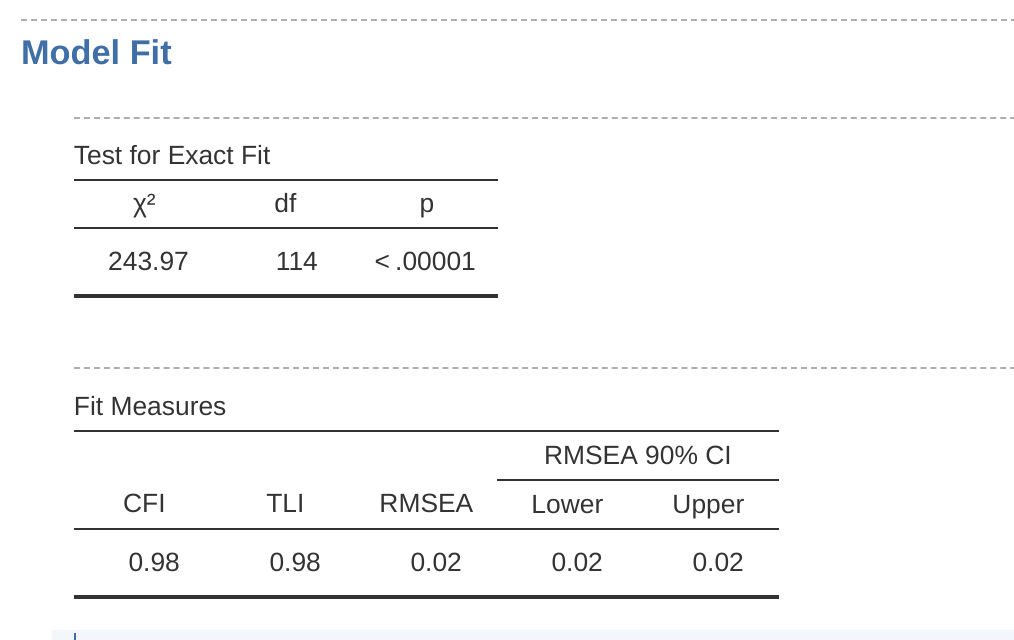
Mirando Figure 15.25 podemos ver que el valor de chi-cuadrado es altamente significativo, lo cual no es una sorpresa dado el gran tamaño de la muestra (N = 2748). El CFI es 0,98 y el TLI también es 0,98, lo que indica un muy buen ajuste. El RMSEA es 0,02 con un intervalo de confianza del 90 % de 0,02 a 0,02, ¡muy ajustado!
En general, creo que podemos estar satisfechos de que nuestro modelo preespecificado se ajusta muy bien a los datos observados, lo que respalda nuestro modelo MTMM para el ASQ.
Ahora podemos pasar a ver las cargas factoriales y las estimaciones de la covarianza factorial, como en Figure 15.26. A menudo, las estimaciones estandarizadas son más fáciles de interpretar y se pueden especificar en la opción ‘Estimaciones’. Estas tablas pueden incorporarse de manera útil en un informe escrito o artículo científico.
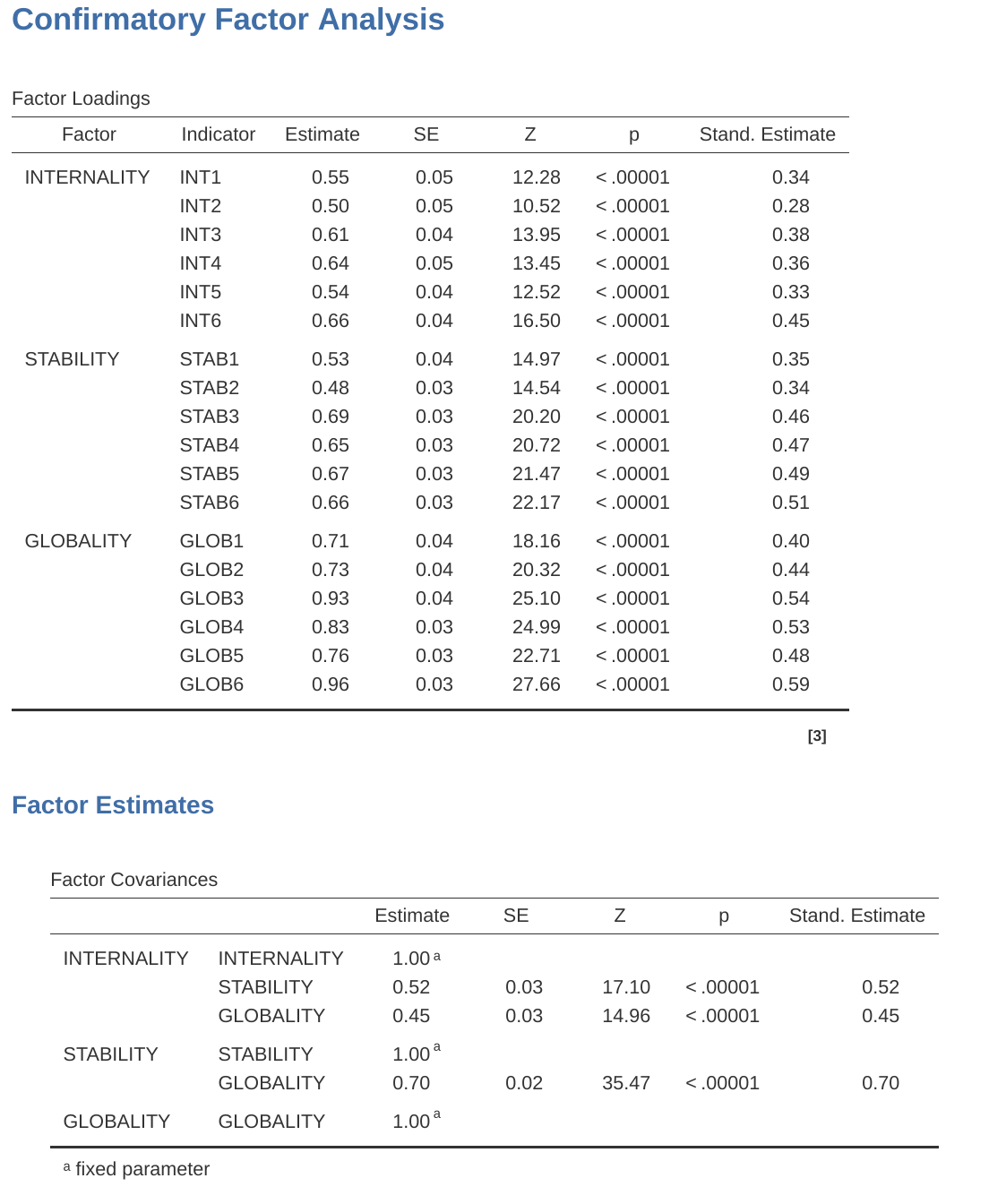
Puede ver en Figure 15.26 que todas nuestras cargas factoriales y covarianzas factoriales preespecificadas son significativamente diferentes de cero. En otras palabras, todos parecen estar haciendo una contribución útil al modelo.
Hemos tenido bastante suerte con este análisis, ¡obteniendo un muy buen ajuste en nuestro primer intento!
15.5 Análisis de confiabilidad de consistencia interna
Después de haber pasado por el proceso de desarrollo de escala inicial utilizando EFA y CFA, debería haber llegado a una etapa en la que la escala se sostiene bastante bien usando CFA con diferentes muestras. Una cosa que también le puede interesar en esta etapa es ver qué tan bien se miden los factores usando una escala que combina las variables observadas.
En psicometría, utilizamos el análisis de confiabilidad para proporcionar información sobre la consistencia con la que una escala mide una construcción psicológica (consulte la sección anterior sobre Section 2.3). La consistencia interna es lo que nos preocupa aquí, y se refiere a la consistencia entre todos los elementos individuales que componen una escala de medición. Entonces, si tenemos \(V1, V2, V3, V4\) y \(V5\) como variables de elementos observados, entonces podemos calcular una estadística que nos diga qué tan consistentes internamente son estos elementos para medir la construcción subyacente.
Una estadística popular utilizada para verificar la consistencia interna de una escala es el alfa de Cronbach (Chronbach, 1951). El alfa de Cronbach es una medida de equivalencia (si diferentes conjuntos de elementos de la escala darían los mismos resultados de medición). La equivalencia se prueba dividiendo los ítems de la escala en dos grupos (una “mitad dividida”) y viendo si el análisis de las dos partes da resultados comparables. Por supuesto, hay muchas formas de dividir un conjunto de elementos, pero si se realizan todas las divisiones posibles, es posible generar una estadística que refleje el patrón general de los coeficientes de división por mitades. El alfa de Cronbach (\(\alpha\)) es una estadística de este tipo: una función de todos los coeficientes divididos por la mitad de una escala. Si un conjunto de elementos que miden un constructo (por ejemplo, una escala de Extraversión) tiene un \(\alpha\) de \(0,80\), entonces la proporción de la varianza del error en la escala es de \(0,20\). En otras palabras, una escala con \(\alpha\) de \(0.80\) incluye aproximadamente un 20% de error.
PERO, (y ese es un GRAN “PERO”), el alfa de Cronbach no es una medida de unidimensionalidad (es decir, un indicador de que una escala mide un solo factor o construcción en lugar de múltiples construcciones relacionadas). Las escalas que son multidimensionales harán que se subestime alfa si no se evalúan por separado para cada dimensión, pero los valores altos de alfa no son necesariamente indicadores de unidimensionalidad. Por lo tanto, un \(\alpha\) de 0,80 no significa que se tenga en cuenta el 80 % de una única construcción subyacente. Podría ser que el 80% provenga de más de una construcción subyacente. Es por eso que EFA y CFA son útiles para hacer primero.
Además, otra característica de \(\alpha\) es que tiende a ser específico de la muestra: no es una característica de la escala, sino una característica de la muestra en la que se ha utilizado la escala. Una muestra sesgada, no representativa o pequeña podría producir un coeficiente \(\alpha\) muy diferente al de una muestra grande y representativa. \(\alpha\) incluso puede variar de una muestra grande a una muestra grande. Sin embargo, a pesar de estas limitaciones, el \(\alpha\) de Cronbach ha sido popular en Psicología para estimar la confiabilidad de la consistencia interna. Es bastante fácil de calcular, comprender e interpretar y, por lo tanto, puede ser una verificación inicial útil del rendimiento de la báscula cuando administra una báscula con una muestra diferente, de un entorno o población diferente, por ejemplo.
Una alternativa es Omega de McDonald’s (\(\omega\)), y jamovi también proporciona esta estadística. Mientras que \(\alpha\) hace las siguientes suposiciones: (a) no hay correlaciones residuales, (b) los elementos tienen cargas idénticas y (c) la escala es unidimensional, \(\omega\) no lo hace y, por lo tanto, es una estadística de confiabilidad más robusta. Si no se violan estas suposiciones, \(\alpha\) y \(\omega\) serán similares, pero si lo son, entonces se preferirá \(\omega\).
A veces se proporciona un umbral para \(\alpha\) o \(\omega\), lo que sugiere un valor “suficientemente bueno”. Esto podría ser algo así como \(\alpha\)s de \(0.70\) o \(0.80\) que representan confiabilidad “aceptable” y “buena”, respectivamente. Sin embargo, esto depende de lo que se supone que mida exactamente la báscula, por lo que los umbrales como este deben usarse con precaución. Podría ser mejor decir simplemente que un \(\alpha\) o \(\omega\) de \(0,70\) está asociado con una varianza de error del 30 % en una escala, y un \(\alpha\) o \(\omega\) de \(0,80\) está asociado con 20 %
¿Puede \(\alpha\) ser demasiado alto? Probablemente: si obtiene un coeficiente \(\alpha\) por encima de \(0,95\), esto indica una alta intercorrelación entre los elementos y que podría haber demasiada especificidad demasiado redundante en la medición, con el riesgo de que el constructo que se mide sea quizás demasiado angosto.
15.5.1 Análisis de confiabilidad en jamovi
Tenemos una tercera muestra de datos de personalidad para usar para realizar análisis de confiabilidad: en el archivo bfi_sample3.csv. Una vez más, verifique que las 25 variables del ítem de personalidad estén codificadas como continuas. Para realizar un análisis de confiabilidad en jamovi:
Seleccione Factor - Análisis de confiabilidad en la barra de botones principal de jamovi para abrir la ventana de análisis de confiabilidad (Figure 15.27).
Seleccione las variables 5 A y transfiéralas al cuadro ‘Artículos’.
En la opción “Elementos de escala inversa”, seleccione la variable A1 en el cuadro “Elementos de escala normal” y muévalo al cuadro “Elementos de escala inversa”.
Verifique otras opciones apropiadas, como en Figure 15.27.

Una vez hecho esto, mira la ventana de resultados de jamovi. Deberías ver algo como Figure 15.28. Esto nos dice que el coeficiente \(\alpha\) de Cronbach para la escala de Amabilidad es 0,72. Esto significa que poco menos del 30 % de la puntuación de la escala de Amabilidad es una varianza del error. También se da \(\omega\) de McDonald’s, y esto es 0.74, no muy diferente de \(\alpha\).

También podemos comprobar cómo se puede mejorar \(\alpha\) o \(\omega\) si se elimina un elemento específico de la escala. Por ejemplo, \(\alpha\) aumentaría a 0,74 y \(\omega\) a 0,75 si elimináramos el elemento A1. Este no es un gran aumento, por lo que probablemente no valga la pena hacerlo.
El proceso de cálculo y verificación de las estadísticas de la báscula (\(\alpha\) y \(\omega\)) es el mismo para todas las demás básculas, y todas tenían estimaciones de confiabilidad similares, excepto Openness. Para la Apertura, la cantidad de variación del error en la puntuación de la escala es de alrededor del 40 %, lo cual es alto e indica que la Apertura es sustancialmente menos consistente como medida confiable de un atributo de personalidad que las otras escalas de personalidad.
15.6 Resumen
En este capítulo sobre análisis factorial y técnicas relacionadas, presentamos y demostramos análisis estadísticos que evalúan el patrón de relaciones en un conjunto de datos. Específicamente, hemos cubierto:
Análisis Factorial Exploratorio (AFE). EFA es una técnica estadística para identificar factores latentes subyacentes en un conjunto de datos. Cada variable observada se conceptualiza como una representación del factor latente hasta cierto punto, indicado por una carga factorial. Los investigadores también utilizan EFA como una forma de reducción de datos, es decir, identificando variables observadas que pueden combinarse en nuevas variables de factores para análisis posteriores.
Análisis de componentes principales (PCA) es una técnica de reducción de datos que, estrictamente hablando, no identifica factores latentes subyacentes. En cambio, PCA simplemente produce una combinación lineal de variables observadas.
Análisis Factorial Confirmatorio (CFA). A diferencia de EFA, con CFA comienza con una idea, un modelo, de cómo las variables en sus datos se relacionan entre sí. Luego, prueba tu modelo con los datos observados y evalúa qué tan bien se ajusta el modelo a los datos.
En [Multi-Trait Multi-Method CFA] (MTMM CFA), tanto el factor latente como la varianza del método se incluyen en el modelo en un enfoque que es útil cuando se utilizan diferentes enfoques metodológicos y, por lo tanto, la varianza del método es una consideración importante.
[Análisis de fiabilidad de la consistencia interna]. Esta forma de análisis de confiabilidad prueba cuán consistentemente una escala mide una construcción de medición (psicológica).
muy útil, las cargas factoriales se pueden interpretar como coeficientes de regresión estandarizados↩︎
las rotaciones oblicuas proporcionan dos matrices de factores, una denominada matriz de estructura y otra denominada matriz de patrón. En jamovi, solo se muestra la matriz de patrones en los resultados, ya que suele ser la más útil para la interpretación, aunque algunos expertos sugieren que ambos pueden ser útiles. En una matriz de estructura, los coeficientes muestran la relación entre la variable y los factores mientras ignoran la relación de ese factor con todos los demás factores (es decir, una correlación de orden cero). Los coeficientes de matriz de patrones muestran la contribución única de un factor a una variable mientras controlan los efectos de otros factores en esa variable (similar al coeficiente de regresión parcial estandarizado). Bajo rotación ortogonal, los coeficientes de estructura y patrón son los mismos.↩︎
a veces se informa en el análisis factorial la “comunalidad”, que es la cantidad de varianza en una variable que se explica por la solución factorial. Unicidad es igual a (1 \(\sum\) comunalidad)↩︎
recordar primero revertir la puntuación de algunas variables si es necesario↩︎
aparte, dado que teníamos una idea bastante firme de nuestros factores “putativos” iniciales, podríamos haber ido directamente a CFA y omitir el paso de EFA. Ya sea que use EFA y luego pase a CFA, o vaya directamente a CFA, es una cuestión de juicio y qué tan seguro está inicialmente de que tiene el modelo correcto (en términos de número de factores y variables). Más temprano en el desarrollo de escalas, o en la identificación de construcciones latentes subyacentes, los investigadores tienden a usar EFA. Más tarde, a medida que se acercan a una escala final, o si quieren verificar una escala establecida en una nueva muestra, CFA es una buena opción.↩︎