11 Comparar dos medias

En Chapter 10 cubrimos la situación en la que tanto la variable de resultado como la variable predictora estaban en una escala nominal. Muchas situaciones del mundo real presentan esa característica, por lo que encontrarás que las pruebas de ji-cuadrado en particular se usan bastante. Sin embargo, es mucho más probable que te encuentres en una situación en la que tu variable de resultado esté en una escala de intervalo o mayor, y lo que te interese es si el valor promedio de la variable de resultado es mayor en un grupo u otro. Por ejemplo, una psicóloga podría querer saber si los niveles de ansiedad son más altos entre los padres que entre los que no son padres, o si la capacidad de la memoria de trabajo se reduce al escuchar música (en relación con no escuchar música). En un contexto médico, podríamos querer saber si un nuevo medicamento aumenta o disminuye la presión arterial. Un científico agrícola podría querer saber si agregar fósforo a las plantas nativas australianas las matará.¹ En todas estas situaciones, nuestra variable de resultado es una variable continua, con escala de intervalo o de razón, y nuestro predictor es una variable de “agrupación” binaria. En otras palabras, queremos comparar las medias de los dos grupos.

Para comparar medias se utiliza una prueba t, de la cual hay diversas variedades dependiendo exactamente de qué pregunta quieras resolver. Como consecuencia, la mayor parte de este capítulo se centra en diferentes tipos de pruebas t: pruebas t de una muestra, pruebas t de muestras independientes y pruebas t de muestras relacionadas. Luego hablaremos sobre las pruebas unilaterales y, después, hablaremos un poco sobre la d de Cohen, que es la medida estándar del tamaño del efecto para una prueba t. Las últimas secciones del capítulo se centran en los supuestos de las pruebas t y los posibles remedios si se violan. Sin embargo, antes de discutir cualquiera de estas cosas, comenzaremos con una discusión sobre la prueba z.

11.1 La prueba z de una muestra

En esta sección describiré una de las pruebas más inútiles de toda la estadística: la prueba z. En serio, esta prueba casi nunca se usa en la vida real. Su único propósito real es que, al enseñar estadística, es un trampolín muy conveniente en el camino hacia la prueba t, que es probablemente la herramienta más (sobre)utilizada en estadística.

11.1.1 El problema de inferencia que aborda la prueba

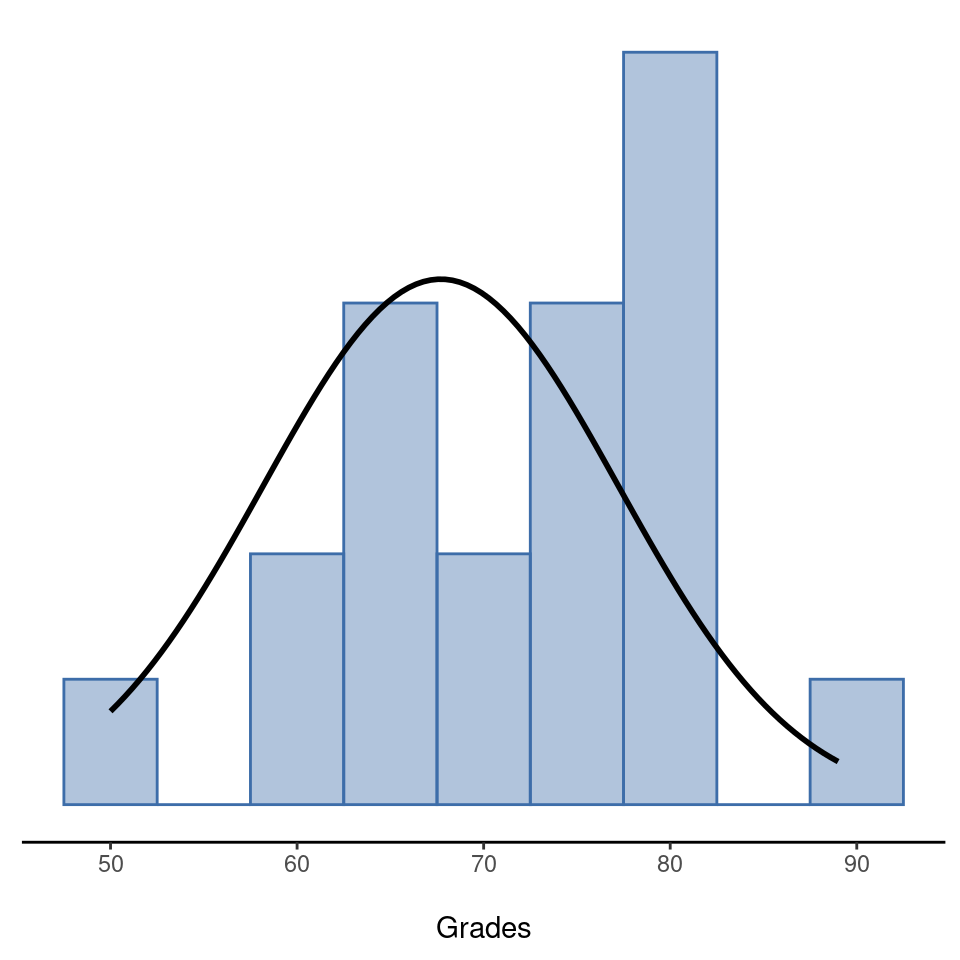
Para presentar la idea que subyace a la prueba z, usemos un ejemplo sencillo. Un amigo mío, el Dr. Zeppo, califica su clase de introducción a la estadística en una curva. Supongamos que la calificación promedio en su clase es de $67.5$ y la desviación estándar es de $9.5$. De sus muchos cientos de estudiantes, resulta que 20 de ellos también reciben clases de psicología. Por curiosidad, me pregunto si los estudiantes de psicología tienden a obtener las mismas calificaciones que todos los demás (es decir, $67.5 $ promedio) o si tienden a obtener una puntuación más alta o más baja. Me envía por correo electrónico el archivo zeppo.csv, que uso para ver las calificaciones de esos estudiantes, en la vista de hoja de cálculo jamovi, y luego calculo la media en ‘Exploración’ - ‘Descriptivos’ ². El valor medio es $72.3$.

50 60 60 64 66 66 67 69 70 74 76 76 77 79 79 79 81 82 82 89

Mmm. Puede ser que los estudiantes de psicología estén sacando notas un poco más altas de lo normal. Esa media muestral de $\bar{X} = 72,3$ es un poco más alta que la media hipotética de la población de $\mu = 67,5$ pero, por otro lado, un tamaño muestral de $N = 20$ no es tan grande. Tal vez sea pura casualidad.

Para responder a la pregunta, ayuda poder escribir qué es lo que creo que sé. En primer lugar, sé que la media muestral es $\bar{X} = 72,3$. Si estoy dispuesta a asumir que el alumnado de psicología tiene la misma desviación estándar que el resto de la clase, entonces puedo decir que la desviación estándar de la población es $\sigma = 9.5$. También supondré que dado que el Dr. Zeppo está calificando en una curva, las calificaciones de los y las estudiantes de psicología se distribuyen normalmente.

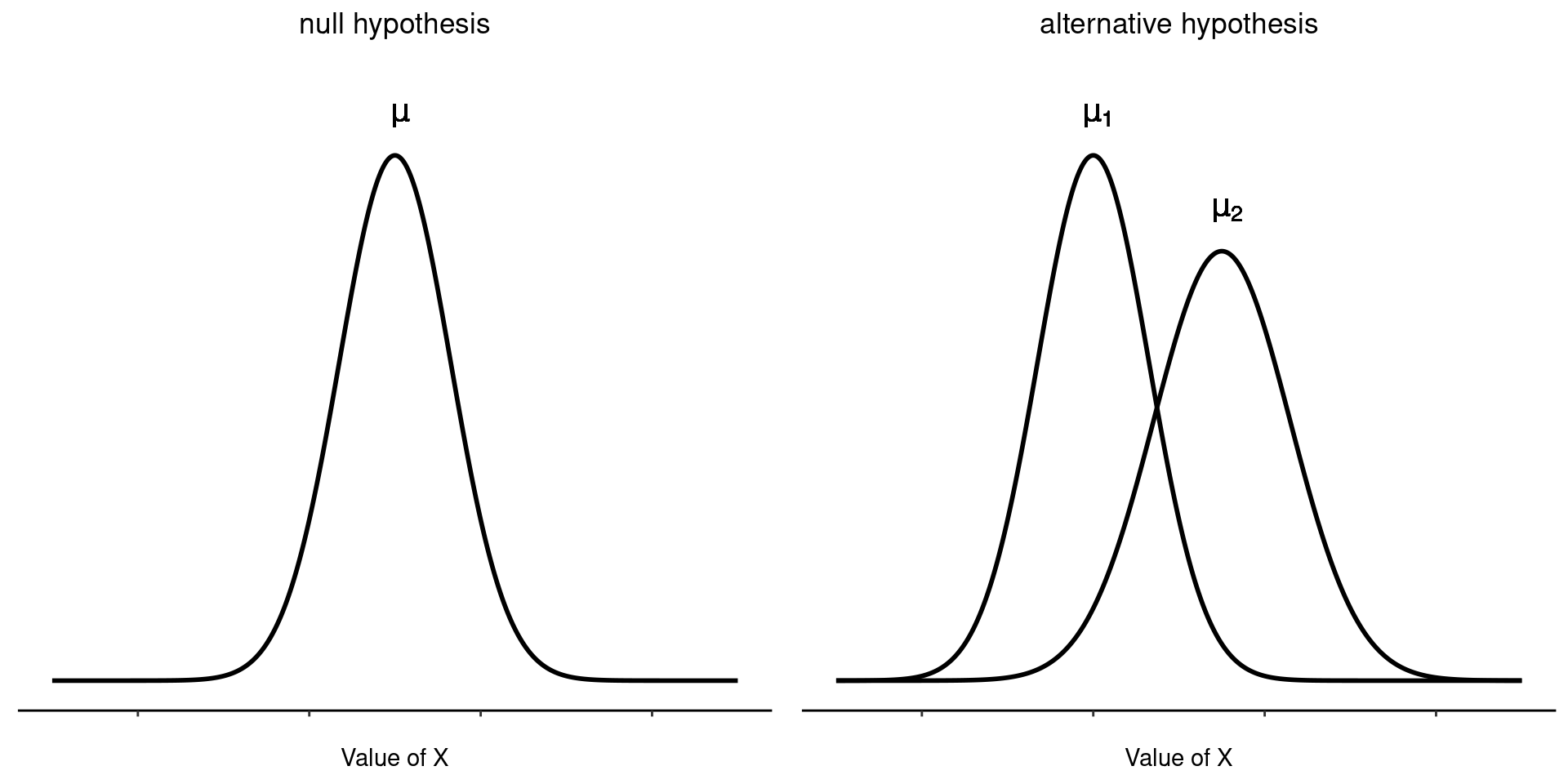
A continuación, ayuda tener claro lo que quiero aprender de los datos. En este caso mi hipótesis de investigación se relaciona con la media poblacional $\mu$ para las calificaciones del alumnado de psicología, la cual se desconoce. Específicamente quiero saber si $\mu = 67.5$ o no. Dado que esto es lo que sé, ¿podemos idear una prueba de hipótesis para resolver nuestro problema? Los datos, junto con la distribución hipotética de la que se cree que surgen, se muestran en Figure 11.1. No es del todo obvio cuál es la respuesta correcta, ¿verdad? Para ello, vamos a necesitar algunos estadísticos.

Figure 11.1: La distribución teórica (línea sólida) a partir de la cual se supone que se generaron las calificaciones (barras) de los estudiantes de psicología

11.1.2 Construyendo la prueba de hipótesis

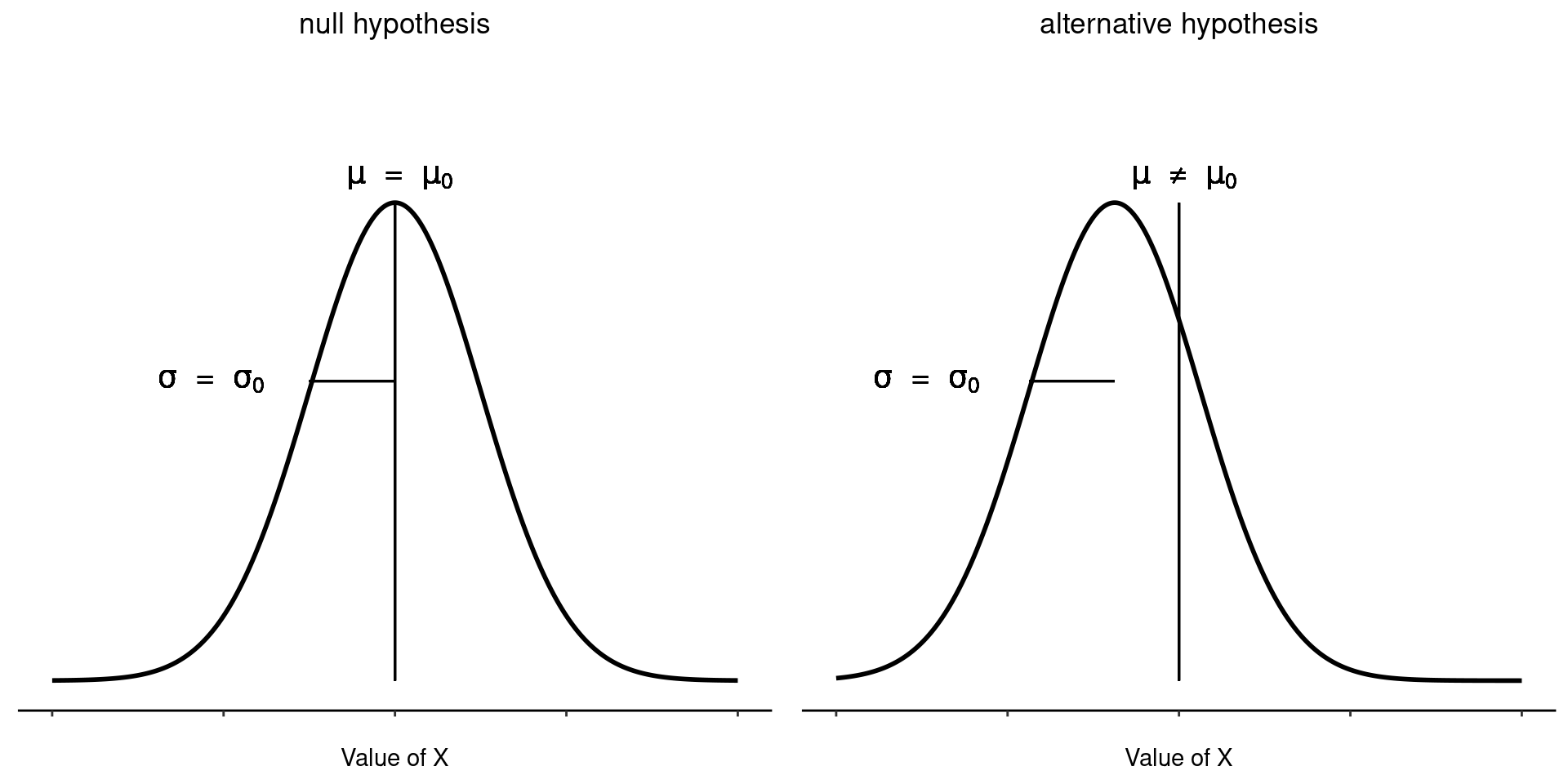
El primer paso para construir una prueba de hipótesis es tener claro cuáles son las hipótesis nula y alternativa. Esto no es demasiado difícil. Nuestra hipótesis nula, $H_0$, es que la verdadera media poblacional $\mu$ para las calificaciones de los estudiantes de psicología es $67,5\%$, y nuestra hipótesis alternativa es que la media poblacional no es $67,5\%$. Si escribimos esto en notación matemática, estas hipótesis se convierten en:

\[ H_0:\mu= 67.5 \] \[ H_1:\mu \neq 67.5 \]

aunque, para ser sincera, esta notación no añade mucho a nuestra comprensión del problema, es solo una forma compacta de escribir lo que estamos tratando de aprender de los datos. Las hipótesis nulas $H_0$ alternativa $H_1$ para nuestra prueba se ilustran en Figure 11.2. Además de ofrecernos estas hipótesis, el escenario descrito anteriormente nos proporciona una buena cantidad de conocimientos previos que podrían ser útiles. En concreto, hay dos datos especiales que podemos añadir:

Las calificaciones de psicología se distribuyen normalmente.
Se sabe que la verdadera desviación estándar de estas puntuaciones $\sigma$ es 9,5.

Por el momento, actuaremos como si estos fueran hechos absolutamente fiables. En la vida real, este tipo de conocimiento de fondo absolutamente fiable no existe, por lo que si queremos confiar en estos hechos, solo tendremos que suponer que estas cosas son ciertas. Sin embargo, dado que estas suposiciones pueden o no estar justificadas, es posible que debamos verificarlas. Sin embargo, por ahora, mantendremos las cosas simples.

Figure 11.2: Ilustración gráfica de las hipótesis nula y alternativa asumidas por la prueba $z$ de una muestra (es decir, la versión de dos colas). Tanto la hipótesis nula como la alternativa suponen que la distribución de la población es normal y, además, suponen que se conoce la desviación estándar de la población (fijada en algún valor $\$sigma_0$). La hipótesis nula (izquierda) es que la media poblacional $\mu$ es igual a algún valor especificado $\mu_0$. La hipótesis alternativa (derecha) es que la media poblacional difiere de este valor, $\mu \neq \mu_0$

El siguiente paso es averiguar cuál sería una buena opción para la prueba estadística, algo que nos ayudará a discriminar entre $H_0$ y $H_1$. Dado que todas las hipótesis se refieren a la media de la población $\mu$, la media de la muestra $\bar{X}$ sería un punto de partida muy útil. Lo que podríamos hacer es observar la diferencia entre la media muestral $\bar{X}$ y el valor que predice la hipótesis nula para la media poblacional. En nuestro ejemplo, eso significaría que calculamos $\bar{X} - 67.5$. De forma más general, si hacemos que $\mu_0$ se refiera al valor que la hipótesis nula afirma que es nuestra media poblacional, entonces querríamos calcular

\[\bar{X}-\mu_0\]

Si esta cantidad es igual o está muy cerca de 0, las cosas pintan bien para la hipótesis nula. Si esta cantidad está muy lejos de 0, entonces parece menos probable que valga la pena mantener la hipótesis nula. Pero, ¿a qué distancia de cero debería estar para que rechacemos H0?

Para averiguarlo necesitaremos confiar en esos dos conocimientos previos que mencioné anteriormente; es decir, que los datos sin procesar se distribuyen normalmente y que conocemos el valor de la desviación estándar de la población $\sigma$. Si la hipótesis nula es realmente verdadera y la media verdadera es $\mu_0$, entonces estos hechos juntos significan que conocemos la distribución completa de la población de los datos: una distribución normal con media $\mu_0$ y desviación estándar $\sigma$ .³

Bien, si eso es cierto, ¿qué podemos decir sobre la distribución de $\bar{X}$? Bueno, como discutimos anteriormente (ver Section 8.3.3), la distribución muestral de la media $\bar{X}$ también es normal, y tiene media $\mu$. Pero la desviación estándar de esta distribución muestral $\\{se(\bar{X})\\}$, que se denomina error estándar de la media, es ⁴

\[se(\bar{X})=\frac{\sigma}{\sqrt{N}}\]

Ahora viene el truco. Lo que podemos hacer es convertir la media muestral $\bar{X}$ en una puntuación estándar (ver Section 4.5). Esto se escribe convencionalmente como z, pero por ahora me referiré a él como $z_{\bar{X}}$. Uso esta notación expandida para ayudarte a recordar que estamos calculando una versión estandarizada de una media muestral, no una versión estandarizada de una sola observación, que es a lo que generalmente se refiere una puntuación z. Cuando lo hacemos, la puntuación z para nuestra media muestral es

\[z_{\bar{X}}=\frac{\bar{X}-\mu_0}{SE(\bar{X})}\] o, equivalentemente

\[z_{\bar{X}}=\frac{\bar{X}-\mu_0}{\frac{\sigma}{\sqrt{N}}}\]

Esta puntuación z es nuestra prueba estadística. Lo bueno de usar esto como nuestra prueba estadística es que, como todas las puntuaciones z, tiene una distribución normal estándar:⁵

En otras palabras, independientemente de la escala en la que se encuentren los datos originales, el estadístico z siempre tiene la misma interpretación: es igual a la cantidad de errores estándar que separan la media muestral observada $\bar{X}$ de la media poblacional $\mu_0$ predicha por la hipótesis nula. Mejor aún, independientemente de cuáles sean realmente los parámetros poblacionales para las puntuaciones sin procesar, las regiones críticas del 5% para la prueba z son siempre las mismas, como se ilustra en Figure 11.3. Y lo que esto significaba, en los tiempos en que la gente hacía todos sus cálculos a mano, es que alguien podía publicar una tabla como Table 11.1. Esto, a su vez, significó que los investigadores pudieran calcular su estadístico z a mano y luego buscar el valor crítico en un libro de texto.

\[z_{\bar{X}} \sum Normal(0,1)\]

Table 11.1:
valores críticos para diferentes niveles alfa
	critical z value
desired $\alpha$ level	two-sided test	one-sided test
.1	1.644854	1.281552
.05	1.959964	1.644854
.01	2.575829	2.326348
.001	3.290527	3.090232

11.1.3 Un ejemplo práctico, a mano

Ahora, como mencioné anteriormente, la prueba z casi nunca se usa en la práctica. Se usa tan raramente en la vida real que la instalación básica de jamovi no tiene una función integrada para ello. Sin embargo, la prueba es tan increíblemente simple que es muy fácil hacerla manualmente. Volvamos a los datos de la clase del Dr. Zeppo. Habiendo cargado los datos de calificaciones, lo primero que debo hacer es calcular la media de la muestra, lo cual ya hice ($72.3$). Ya tenemos la desviación estándar poblacional conocida ($\sigma = 9.5$), y el valor de la media poblacional que especifica la hipótesis nula ($\mu_0 = 67.5$), y conocemos el tamaño de la muestra ($N=20$).

Figure 11.3: Regiones de rechazo para la prueba z de dos colas (panel (a)) y la prueba z de una cola (panel (b))

A continuación, calculemos el error estándar (verdadero) de la media (fácil de hacer con una calculadora):

\[ \begin{split} sem.true & = \frac{sd.true}{\sqrt{N}} \\\\ & = \frac{9.5}{\sqrt{20}} \\\\ & = 2.124265 \end{split} \]

Y finalmente, calculamos nuestra puntuación z:

\[ \begin{split} z.score & = \frac{sample.mean - mu.null}{sem.true} \\\\ & = \frac{ (72.3 - 67.5)}{ 2.124265} \\\\ & = 2.259606 \end{split} \]

En este punto, tradicionalmente buscaríamos el valor $2.26$ en nuestra tabla de valores críticos. Nuestra hipótesis original era de dos colas (realmente no teníamos ninguna teoría sobre si los estudiantes de psicología serían mejores o peores en estadística que otros estudiantes), por lo que nuestra prueba de hipótesis también es bilateral (o de dos colas). Mirando la pequeña tabla que mostré anteriormente, podemos ver que $2.26$ es mayor que el valor crítico de $1.96$ que se requeriría para ser significativo en $\alpha = .05$, pero menor que el valor de $2.58$ que se requeriría para que sea significativo a un nivel de $\alpha = .01$. Por lo tanto, podemos concluir que tenemos un efecto significativo, que podríamos escribir diciendo algo como esto:

Con una nota media de $73,2$ en la muestra de estudiantes de psicología, y asumiendo una desviación estándar poblacional real de $9,5$, podemos concluir que los y las estudiantes de psicología tienen puntuaciones en estadística significativamente diferentes a la media de la clase ($z = 2,26, N = 20, p<.05$).

11.1.4 Supuestos de la prueba z

Como he dicho antes, todas las pruebas estadísticas tienen supuestos. Algunas pruebas tienen supuestos razonables, mientras que otras no. La prueba que acabo de describir, la prueba z de una muestra, hace tres suposiciones básicas. Estas son:

Normalidad. Como suele describirse, la prueba z supone que la verdadera distribución de la población es normal.⁶ Suele ser un supuesto bastante razonable, y es un supuesto que podemos verificar si nos preocupa (consulta la Sección sobre [Comprobación de la normalidad de una muestra]).
Independencia. El segundo supuesto de la prueba es que las observaciones en su conjunto de datos no están correlacionadas entre sí, o relacionadas entre sí de alguna manera divertida. Esto no es tan fácil de verificar estadísticamente, depende un poco de un buen diseño experimental. Un ejemplo obvio (y estúpido) de algo que viola este supuesto es un conjunto de datos en el que “copias” la misma observación una y otra vez en tu archivo de datos para que termines con un “tamaño de muestra” masivo, que consiste solo en una observación genuina. De manera más realista, debes preguntarte si es realmente plausible imaginar que cada observación es una muestra completamente aleatoria de la población que te interesa. En la práctica, este supuesto nunca se cumple, pero hacemos todo lo posible para diseñar estudios que minimicen los problemas de los datos correlacionados.
Desviación estándar conocida. El tercer supuesto de la prueba z es que el investigador conoce la verdadera desviación estándar poblacional. Esto es una estupidez. En ningún problema de análisis de datos del mundo real conoces la desviación estándar σ de alguna población pero ignoras por completo la media $\mu$. En otras palabras, este supuesto siempre es incorrecto.

En vista de la estupidez de suponer que se conoce $\alpha$, veamos si podemos vivir sin ello. ¡Esto nos saca del lúgubre dominio de la prueba z y nos lleva al reino mágico de la prueba t, con unicornios, hadas y duendes!

11.2 La prueba t de una muestra

Después de pensarlo un poco, decidí que no sería seguro asumir que las calificaciones de los estudiantes de psicología necesariamente tienen la misma desviación estándar que los otros estudiantes en la clase del Dr. Zeppo. Después de todo, si considero la hipótesis de que no tienen la misma media, ¿por qué debería creer que tienen la misma desviación estándar? En vista de esto, debería dejar de asumir que conozco el verdadero valor de $\sigma$. Esto viola los supuestos de mi prueba z, por lo que, en cierto sentido, vuelvo al punto de partida. Sin embargo, no es que me falten opciones. Después de todo, todavía tengo mis datos sin procesar, y esos datos sin procesar me dan una estimación de la desviación estándar de la población, que es 9,52. En otras palabras, aunque no puedo decir que sé que $\sigma = 9,5$, puedo decir que $\hat{\sigma}$ = 9,52.

Está bien, genial. Lo más obvio que podría hacer es ejecutar una prueba z, pero usando la desviación estándar estimada de $9.52$ en lugar de confiar en mi suposición de que la verdadera desviación estándar es $9.5$. Y probablemente no te sorprenda saber que esto aún nos daría un resultado significativo. Este enfoque está cerca, pero no es del todo correcto. Debido a que ahora confiamos en una estimación de la desviación estándar poblacional, necesitamos hacer algunos ajustes por el hecho de que tenemos cierta incertidumbre sobre cuál es realmente la desviación estándar poblacional real. Tal vez nuestros datos sean solo una casualidad… tal vez la verdadera desviación estándar poblacional sea $11$, por ejemplo. Pero si eso fuera realmente cierto, y ejecutamos la prueba z asumiendo $\sigma=11$, entonces el resultado terminaría siendo no significativo. Esto es un problema, y es uno que vamos a tener que abordar.

Figure 11.4: Ilustración gráfica de las hipótesis nula y alternativa asumidas por la prueba t de una muestra (bilateral). Ten en cuenta la similitud con la prueba z (Figure 11.2). La hipótesis nula es que la media poblacional $\mu$ es igual a algún valor especificado $\mu_0$, y la hipótesis alternativa es que no lo es. Al igual que la prueba z, asumimos que los datos se distribuyen normalmente, pero no asumimos que la desviación estándar poblacional $\sigma$ se conoce de antemano

11.2.1 Introducción a la prueba t

Esta ambigüedad es molesta y fue resuelta en 1908 por un tipo llamado William Sealy Gosset (Student, 1908), que en ese momento trabajaba como químico para la cervecería Guinness (ver Box (1987)). Debido a que Guinness vio con malos ojos que sus empleados publicaran análisis estadísticos (aparentemente sintieron que era un secreto comercial), publicó el trabajo bajo el seudónimo de “Un estudiante” y, hasta el día de hoy, el nombre completo de la prueba t es en realidad Prueba t de Student. Lo más importante que descubrió Gosset es cómo debemos tener en cuenta el hecho de que no estamos completamente seguras de cuál es la verdadera desviación estándar.⁷ La respuesta es que cambia sutilmente la distribución muestral. En la prueba t, nuestra prueba estadística, ahora llamada estadístico t, se calcula exactamente de la misma manera que mencioné anteriormente. Si nuestra hipótesis nula es que la verdadera media es $\mu$, pero nuestra muestra tiene una media $\bar{X}$ y nuestra estimación de la desviación estándar poblacional es $\hat{\sigma}$, entonces nuestro estadístico t es :

\[ t=\frac{\bar{X}-\mu}{\frac{\hat{\sigma}}{\sqrt{N}}} \]

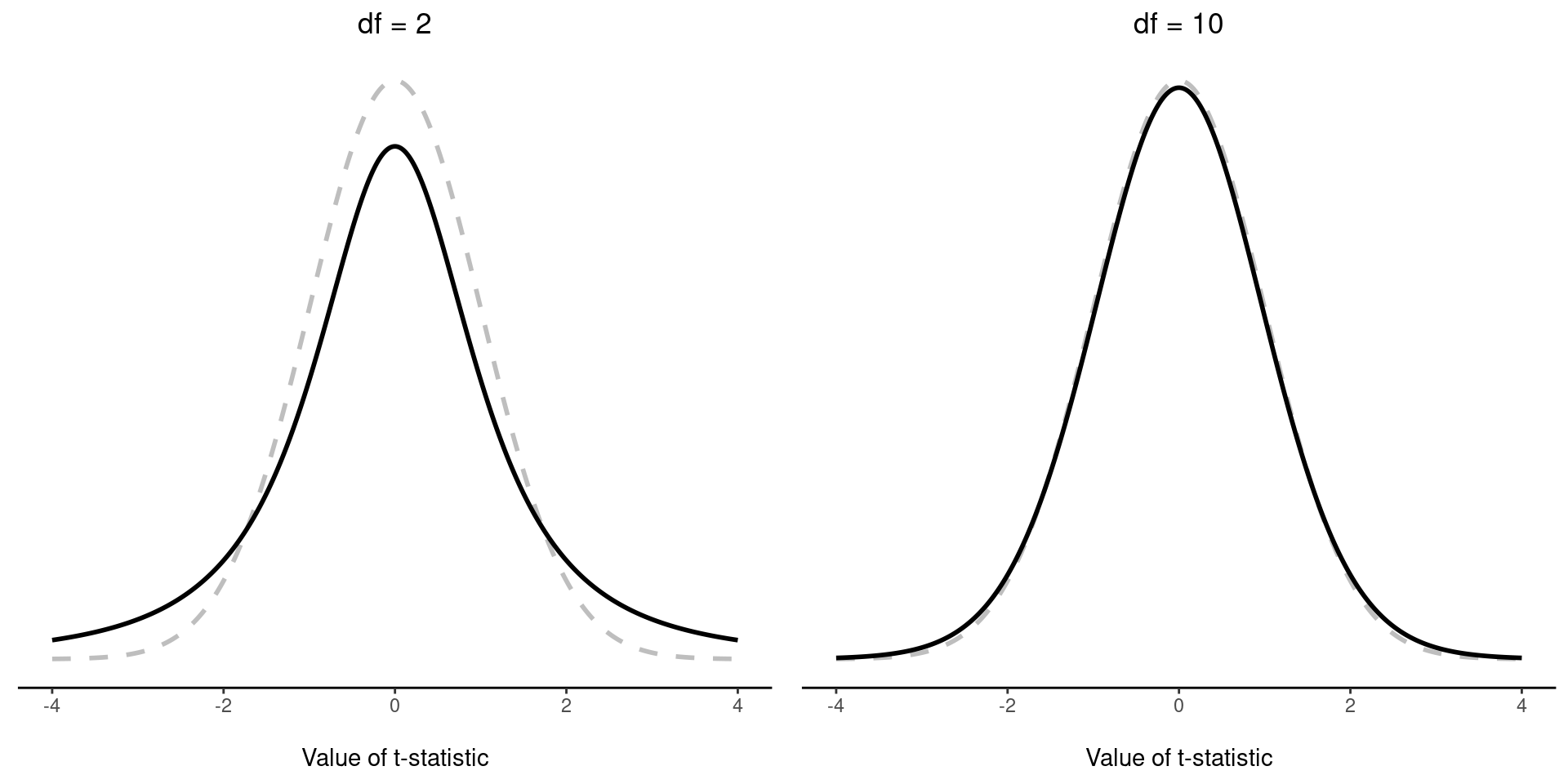
Figure 11.5: Distribución t con 2 grados de libertad (izquierda) y 10 grados de libertad (derecha), con una distribución normal estándar (es decir, media 0 y desviación estándar 1) representada como líneas de puntos a efectos comparativos. Observa que la distribución t tiene colas más pesadas (leptocúrticas, mayor curtosis) que la distribución normal; este efecto es bastante exagerado cuando los grados de libertad son muy pequeños, pero despreciable para valores más grandes. En otras palabras, para $df$ grandes, la distribución t es esencialmente idéntica a una distribución normal.

Lo único que ha cambiado en la ecuación es que en lugar de usar el valor verdadero conocido $\sigma$, usamos la estimación $\hat{\sigma}$. Y si esta estimación se ha construido a partir de N observaciones, entonces la distribución muestral se convierte en una distribución t con $N-1$ grados de libertad (gl). La distribución t es muy similar a la distribución normal, pero tiene colas “más pesadas”, como se explicó anteriormente en Section 7.6 y se ilustró en Figure 11.5. Ten en cuenta, sin embargo, que a medida que gl aumenta, la distribución t empieza a ser idéntica a la distribución normal estándar. Así es como debería ser: si tienes un tamaño de muestra de $N = 70 000 000 $, entonces tu “estimación” de la desviación estándar sería bastante perfecta, ¿verdad? Por lo tanto, debes esperar que para $N$ grandes, la prueba t se comporte exactamente de la misma manera que una prueba z. Y eso es exactamente lo que sucede.

11.2.2 Haciendo la prueba en jamovi

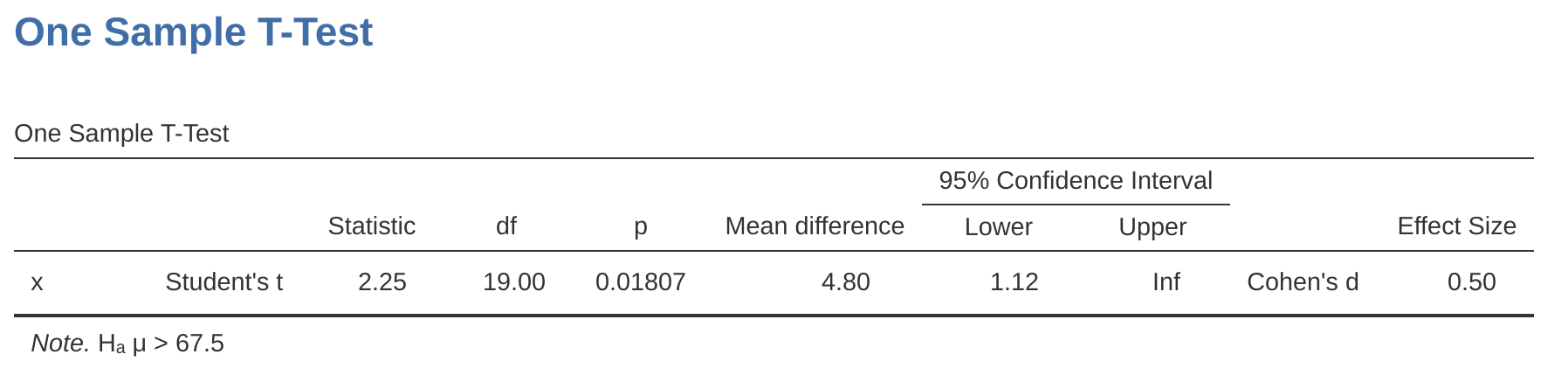
Como era de esperar, la mecánica de la prueba t es casi idéntica a la mecánica de la prueba z. Así que no tiene mucho sentido pasar por el tedioso ejercicio de mostrarte cómo hacer los cálculos usando comandos de bajo nivel. Es prácticamente idéntico a los cálculos que hicimos anteriormente, excepto que usamos la desviación estándar estimada y luego probamos nuestra hipótesis usando la distribución t en lugar de la distribución normal. Entonces, en lugar de pasar por los cálculos en detalle por segunda vez, pasaré directamente a mostraros cómo se realizan realmente las pruebas t. jamovi viene con un análisis dedicado para pruebas t que es muy flexible (se pueden ejecutar muchos tipos diferentes de pruebas t). Es bastante sencillo de usar; todo lo que tienes que hacer es especificar ‘Análisis’ - ‘T-Tests’ - ‘One Sample T-Test’, mover la variable que te interesa (X) al cuadro ‘Variables’ y escribir el valor medio para la hipótesis nula (‘67.5’) en el cuadro ‘Hipótesis’ - ‘Valor de la prueba’. Bastante fácil. Consulta Figure 11.6, que, entre otras cosas a las que llegaremos en un momento, te da una prueba t = 2.25, con 19 grados de libertad y un valor p asociado de $ 0.036 $.

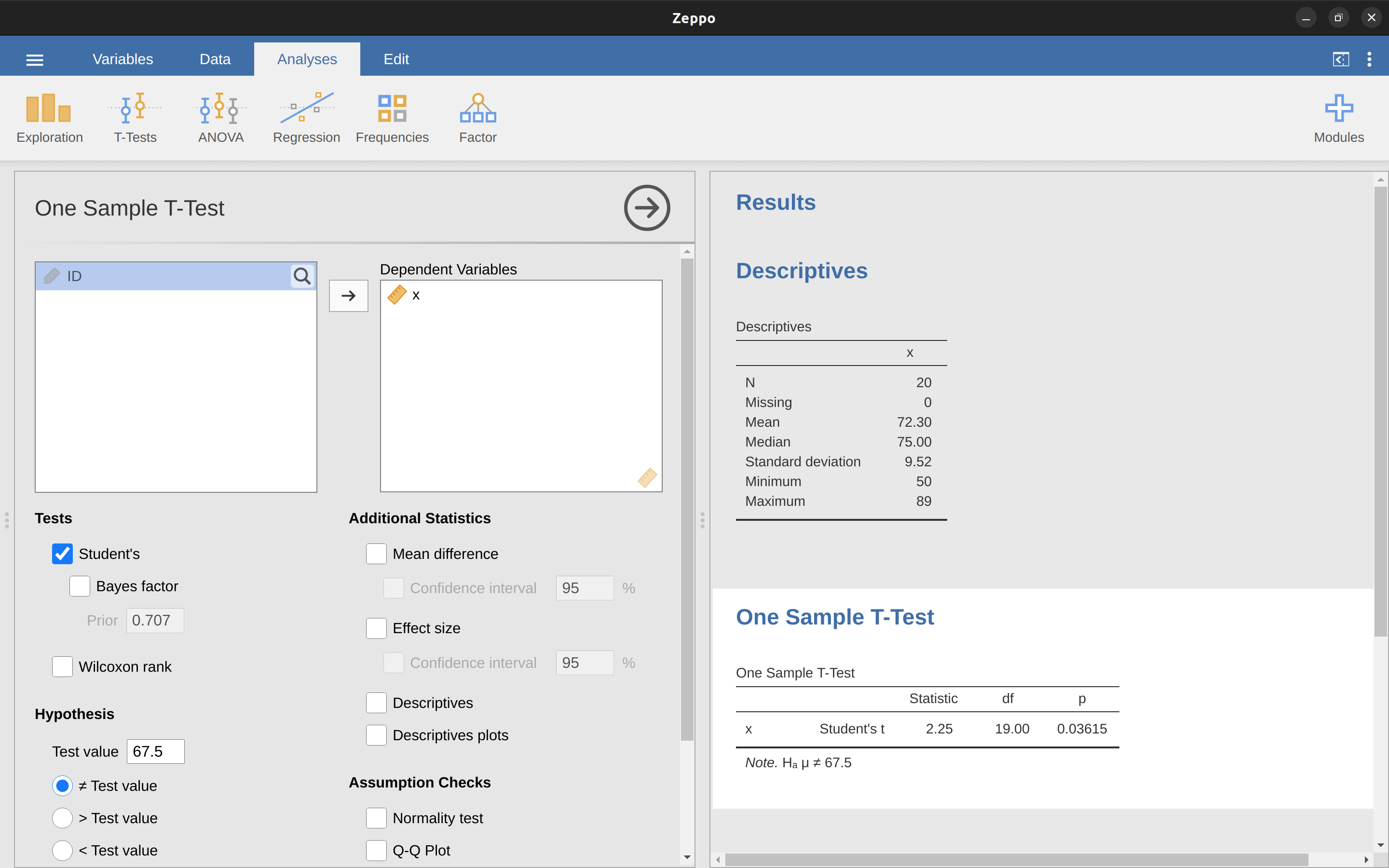
Figure 11.6: jamovi hace la prueba t de una muestra

También se informan otras dos cosas que podrían interesarte: el intervalo de confianza del 95% y una medida del tamaño del efecto (hablaremos más sobre los tamaños del efecto más adelante). Eso parece bastante sencillo. Ahora, ¿qué hacemos con este resultado? Bueno, ya que estamos fingiendo que realmente nos importa mi ejemplo de juguete, nos alegramos al descubrir que el resultado es estadísticamente significativo (es decir, un valor de p por debajo de 0,05). Podríamos informar del resultado diciendo algo así:

Con una nota media de $72,3$, los estudiantes de psicología obtuvieron una puntuación ligeramente superior a la nota media de $67,5$ ($t(19) = 2,25$, $p = 0,036$); la diferencia de medias fue de $4,80$ y el intervalo de confianza de $95\%$ fue de $0,34$ a $9,26$.

…donde $t(19)$ es la notación abreviada de un estadístico t que tiene $19$ grados de libertad. Dicho esto, a menudo no se informa el intervalo de confianza, o se hace usando una forma mucho más reducida que la que he utilizado aquí. Por ejemplo, no es raro ver el intervalo de confianza incluido como parte del bloque de estadísticos después de informar la diferencia media, así:

\[t(19)=2.25, p = .036, CI_{95} = [0.34, 9.26]\]

Con tanta jerga metida en media línea, sabes que debes ser muy inteligente.⁸

11.2.3 Supuestos de la prueba t de una muestra

Bien, entonces, ¿qué supuestos hace la prueba t de una muestra? Bueno, dado que la prueba t es básicamente una prueba z con el supuesto de desviación estándar conocida eliminada, no deberías sorprenderte al ver que hace los mismos supuestos que la prueba z, menos la desviación estándar conocida. Eso es:

Normalidad. Seguimos suponiendo que la distribución poblacional es normal⁹ y, como se indicó anteriormente, existen herramientas estándar que puedes usar para comprobar si se cumple este supuesto ([Comprobar la normalidad de una muestra]), y otras pruebas que puedes hacer en su lugar si se viola este supuesto ([Prueba de datos no normales]).
Independencia. Una vez más, debemos suponer que las observaciones de nuestra muestra se generan independientemente unas de otras. Consulta la discusión anterior sobre la prueba z para obtener información específica (Supuestos de la prueba z).

En general, estos dos supuestos son razonables y, como consecuencia, la prueba t de una muestra se usa bastante en la práctica como una forma de comparar una media muestral con una media poblacional hipotética.

11.3 La prueba t de muestras independientes (prueba de Student)

Aunque la prueba t de una muestra tiene sus usos, no es el ejemplo más típico de una prueba t¹⁰. Una situación mucho más común surge cuando tienes dos grupos diferentes de observaciones. En psicología, esto tiende a corresponder a dos grupos diferentes de participantes, donde cada grupo corresponde a una condición diferente en tu estudio. Para cada persona en el estudio, mides alguna variable de resultado de interés, y la pregunta de investigación que estás haciendo es si los dos grupos tienen o no la misma media poblacional. Esta es la situación para la que está diseñada la prueba t de muestras independientes.

11.3.1 Los datos

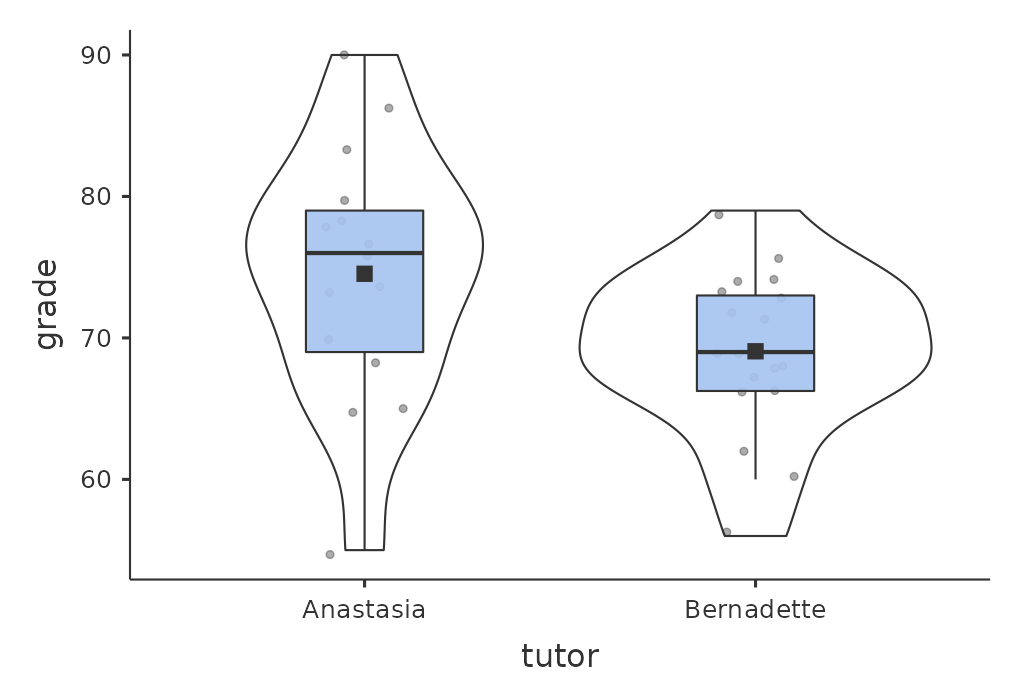
Supongamos que tenemos 33 estudiantes asistiendo a las clases de estadística del Dr. Harpo, y el Dr. Harpo no califica con una curva. En realidad, la calificación del Dr. Harpo es un poco misteriosa, por lo que realmente no sabemos nada sobre cuál es la calificación promedio para la clase en general. En la clase hay dos tutores, Anastasia y Bernadette. Hay $N_1 = 15$ estudiantes en las tutorías de Anastasia y $N_2 = 18$ en las tutorías de Bernadette. La pregunta de investigación que me interesa es si Anastasia o Bernadette son mejores tutoras, o si no hay mucha diferencia. El Dr. Harpo me envía por correo electrónico las calificaciones del curso en el archivo harpo.csv. Como de costumbre, cargaré el archivo en jamovi y veré qué variables contiene: hay tres variables, ID, calificación y tutor. La variable de calificación contiene la calificación de cada estudiante, pero no se importa a jamovi con el atributo de nivel de medición correcto, por lo que necesito cambiar esto para que se considere una variable continua (ver Section 3.6). La variable tutor es un factor que indica quién fue la tutora de cada estudiante, ya sea Anastasia o Bernadette.

Podemos calcular las medias y las desviaciones estándar, utilizando el análisis ‘Exploración’ - ‘descriptivo’, y aquí hay un pequeño cuadro resumen (Table 11.2).

Table 11.2:
cuadro resumen de descriptivos
	mean	std dev	N
Anastasia's students	74.53	9.00	15
Bernadette's students	69.06	5.77	18

Para darte una idea más detallada de lo que está pasando aquí, he trazado diagramas de caja y violín en jamovi, con puntuaciones medias agregadas al diagrama con un pequeño cuadrado sólido. Estos gráficos muestran la distribución de calificaciones para ambas tutoras (Figure 11.7),

11.3.2 Introducción a la prueba

La prueba t de muestras independientes se presenta de dos formas diferentes, la de Student y la de Welch. La prueba t de Student original, que es la que describiré en esta sección, es la más simple de las dos pero se basa en supuestos mucho más restrictivos que la prueba t de Welch. Suponiendo por el momento que deseas ejecutar una prueba bilateral, el objetivo es determinar si se extraen dos “muestras independientes” de datos de poblaciones con la misma media (la hipótesis nula) o diferentes medias (la hipótesis alternativa). Cuando decimos muestras “independientes”, lo que realmente queremos decir aquí es que no existe una relación especial entre las observaciones en las dos muestras. Esto probablemente no tenga mucho sentido en este momento, pero estará más claro cuando hablemos más adelante sobre la prueba t de muestras relacionadas. Por ahora, señalemos que si tenemos un diseño experimental en el que los participantes se asignan aleatoriamente a uno de dos grupos, y queremos comparar el rendimiento medio de los dos grupos en alguna medida de resultado, entonces una prueba t de muestras independientes (en lugar de una prueba t de muestras pareadas) es lo que buscamos.

Figure 11.7: diagramas de caja y violín que muestran la distribución de calificaciones de los estudiantes en las clases de Anastasia y Bernadette. Visualmente, esto sugiere que los estudiantes de la clase de Anastasia pueden estar obteniendo calificaciones ligeramente mejores en promedio, aunque también parecen un poco más variables.

Bien, dejemos que $\mu_1$ denote la media poblacional real para el grupo 1 (p. ej., los estudiantes de Anastasia), y $\mu_2$ será la media poblacional real para el grupo 2 (p. ej., los estudiantes de Bernadette),¹¹ y, como de costumbre, dejaremos que $\bar{X_1}$ y $\bar{X_2}$ denoten las medias muestrales observadas para ambos grupos. Nuestra hipótesis nula establece que las medias de las dos poblaciones son idénticas ($\mu_1 = \mu_2$) y la alternativa a esto es que no lo son ($\mu_1 \neq \mu_2$) (Figure 11.8). Escrito en lenguaje matemático, esto es:

Figure 11.8: Ilustración gráfica de las hipótesis nula y alternativa asumidas por la prueba t de Student. La hipótesis nula supone que ambos grupos tienen la misma media $\mu$, mientras que la alternativa supone que tienen medias diferentes $\mu_1$ y $\mu_2$. Observa que se supone que las distribuciones de la población son normales y que, aunque la hipótesis alternativa permite que el grupo tenga diferentes medias, se supone que tienen la misma desviación estándar.

\[H_0: \mu_1=\mu_2 \] \[H_0: \mu_1 \neq \mu_2 \] Para construir una prueba de hipótesis que maneje este escenario, comenzamos observando que si la hipótesis nula es verdadera, entonces la diferencia entre las medias poblacionales es exactamente cero, $\mu_1-\mu_2 = 0$. Como consecuencia, una prueba estadística se basará en la diferencia entre las medias de las dos muestras. Porque si la hipótesis nula es verdadera, esperaríamos que $\bar{X}_1 - \bar{X}_2$ sea bastante cercano a cero. Sin embargo, tal como vimos con nuestras pruebas de una muestra (es decir, la prueba z de una muestra y la prueba t de una muestra), debemos ser precisos acerca de la proximidad a cero de esta diferencia. Y la solución al problema es más o menos la misma. Calculamos una estimación del error estándar (SE), como la última vez, y luego dividimos la diferencia entre las medias por esta estimación. Por tanto nuestro estadístico t será:

\[t=\frac{\bar{X_1}-\bar{X_2}}{SE}\]

Solo necesitamos averiguar cuál es realmente esta estimación del error estándar. Esto es un poco más complicado que en el caso de cualquiera de las dos pruebas que hemos visto hasta ahora, por lo que debemos analizarlo con mucho más cuidado para comprender cómo funciona.

11.3.3 Una “estimación conjunta” de la desviación estándar

En la “prueba t de Student” original, asumimos que los dos grupos tienen la misma desviación estándar poblacional. Es decir, sin importar si las medias de la población son las mismas, asumimos que las desviaciones estándar de la población son idénticas, $\sigma_1 = \sigma_2$. Dado que asumimos que las dos desviaciones estándar son iguales, quitamos los subíndices y nos referimos a ambos como $\sigma$. ¿Cómo debemos estimar esto? ¿Cómo debemos construir una única estimación de una desviación estándar cuando tenemos dos muestras? La respuesta es, básicamente, las promediamos. Bueno, más o menos. En realidad, lo que hacemos es calcular un promedio ponderado de las estimaciones de varianza, que usamos como nuestra estimación combinada de la varianza. El peso asignado a cada muestra es igual al número de observaciones en esa muestra, menos 1.

[Detalle técnico adicional ¹²]

11.4 Completando la prueba

Independientemente de cómo quieras pensarlo, ahora tenemos nuestra estimación agrupada de la desviación estándar. De ahora en adelante, quitaré el subíndice p y me referiré a esta estimación como $\hat{\sigma}$. Excelente. Ahora volvamos a pensar en la prueba de hipótesis, ¿de acuerdo? La razón principal para calcular esta estimación agrupada era que sabíamos que sería útil a la hora de calcular la estimación del error estándar. Pero ¿error estándar de qué? En la prueba t de una muestra, fue el error estándar de la media muestral, $se(\bar{X})$, y dado que $se(\bar{X}) = \frac{\sigma}{\sqrt {N}}$ ESTE ERA el denominador de nuestra estadística t. Esta vez, sin embargo, tenemos dos medias muestrales. Y lo que nos interesa, específicamente, es la diferencia entre las dos $\bar{X}_1-\bar{X}_2$ Como consecuencia, el error estándar por el que debemos dividir es de hecho el error estándar de la diferencia entre medias.

[Detalle técnico adicional ¹³]

Tal como vimos con nuestra prueba de una muestra, la distribución muestral de este estadístico t es una distribución t (sorprendente, ¿verdad?) siempre que la hipótesis nula sea verdadera y se cumplan todos los supuestos de la prueba. Los grados de libertad, sin embargo, son ligeramente diferentes. Como de costumbre, podemos pensar que los grados de libertad son iguales al número de puntos de datos menos el número de restricciones. En este caso, tenemos N observaciones ($N_1$ en la muestra 1 y $N_2$ en la muestra 2) y 2 restricciones (las medias de la muestra). Entonces, los grados de libertad totales para esta prueba son $N - 2$.

11.4.1 Haciendo la prueba en jamovi

No es sorprendente que puedas ejecutar una prueba t de muestras independientes fácilmente en jamovi. La variable de resultado de nuestra prueba es la nota del alumnado, y los grupos se definen en función de la tutora de cada clase. Así que probablemente no te sorprendas mucho de que todo lo que tienes que hacer en jamovi es ir al análisis relevante (“Análisis” - “T-Tests” - “Independent Samples T-Test”) y mover la variable de calificación al cuadro ‘Variables dependientes’ y la variable de la tutora en el cuadro ‘Variable de agrupación’, como se muestra en Figure 11.9.

Figure 11.9: prueba t para muestras independientes en jamovi, con opciones verificadas para obtener resultados útiles

La salida tiene una forma muy familiar. Primero, te dice qué prueba se ejecutó y te dice el nombre de la variable dependiente que usaste. Luego informa los resultados de la prueba. Al igual que la última vez, los resultados de la prueba consisten en un estadístico t, los grados de libertad y el valor p. La sección final indica dos cosas: el intervalo de confianza y el tamaño del efecto. Hablaré sobre los tamaños del efecto más adelante. Del intervalo de confianza, sin embargo, debería hablar ahora.

Es muy importante tener claro a qué se refiere realmente este intervalo de confianza. Es un intervalo de confianza para la diferencia entre las medias de los grupos. En nuestro ejemplo, los y las estudiantes de Anastasia obtuvieron una calificación promedio de $74,53 $ y el alumnado de Bernadette tuvieron una calificación promedio de $69,06 $, por lo que la diferencia entre las medias de las dos muestras es $5,48 $. Pero, por supuesto, la diferencia entre las medias de la población puede ser mayor o menor que esto. El intervalo de confianza informado en Figure 11.10 te dice que si replicamos este estudio una y otra vez, entonces $ 95 % $ del tiempo, la verdadera diferencia en las medias estaría entre $ 0.20 $ y $ 10.76 $. Consulta Section 8.5 para recordar qué significan los intervalos de confianza.

En cualquier caso, la diferencia entre los dos grupos es significativa (apenas), por lo que podríamos escribir el resultado usando un texto como este:

La nota media en la clase de Anastasia fue de $74,5\%$ (desviación estándar = $9,0$), mientras que la media en la clase de Bernadette fue de $69,1\%$ (desviación estándar = $5,8$). La prueba t de Student de muestras independientes mostró que esta diferencia de $5.4\%$ fue significativa $(t(31) = 2.1, p<.05, CI_{95} = [0.2, 10.8], d = .74)$, lo que sugiere que se ha producido una diferencia genuina en los resultados del aprendizaje.

Observa que he incluido el intervalo de confianza y el tamaño del efecto en el bloque de estadísticos. La gente no siempre lo hace. Como mínimo, esperarías ver el estadístico t, los grados de libertad y el valor p. Entonces deberías incluir algo como esto como mínimo: $t(31) = 2.1, p< .05$. Si los estadísticos se salieran con la suya, todos también informarían el intervalo de confianza y probablemente también la medida del tamaño del efecto, porque son cosas útiles que hay que saber. Pero la vida real no siempre funciona de la forma en que los estadísticos quieren que lo haga, por lo que debes tomar una decisión en función de si crees que ayudará a tus lectores y, si estás escribiendo un artículo científico, el estándar editorial de la revista en cuestión. Algunas revistas esperan que informes los tamaños del efecto, otras no. Dentro de algunas comunidades científicas es una práctica estándar informar intervalos de confianza, en otras no lo es. Tendrás que averiguar qué espera tu audiencia. Pero, para que quede claro, si estás en mi clase, mi posición por defecto es que normalmente merce la pena incluir tanto el tamaño del efecto como el intervalo de confianza.

11.4.2 Valores t positivos y negativos

Antes de pasar a hablar de los supuestos de la prueba t, hay un punto adicional que quiero señalar sobre el uso de las pruebas t en la práctica. El primero se relaciona con el signo del estadístico t (es decir, si es un número positivo o negativo). Una preocupación muy común que tiene el alumnado cuando empieza a realizar su primera prueba t es que a menudo se obtienen valores negativos para el estadístico t y no saben cómo interpretarlo. De hecho, no es nada raro que dos personas que trabajan de forma independiente terminen con resultados casi idénticos, excepto que una persona tiene un valor de t negativo y la otra tiene un valor de t positivo. Si estás ejecutando una prueba bilateral, los valores p serán idénticos. En una inspección más detallada, los estudiantes notarán que los intervalos de confianza también tienen signos opuestos. Está bien. Siempre que esto suceda, encontrarás que las dos versiones de los resultados surgen de formas ligeramente diferentes de ejecutar la prueba t. Lo que está pasando aquí es muy sencillo. El estadístico t que calculamos aquí presenta la siguiente estructura

\[t=\frac{\text{media 1-media 2}}{SE}\]

Si “media 1” es mayor que “media 2”, el estadístico t será positivo, mientras que si “media 2” es mayor, el estadístico t será negativo. De manera similar, el intervalo de confianza que informa jamovi es el intervalo de confianza para la diferencia “(media 1) menos (media 2)”, que será la inversa de lo que obtendrías si estuvieras calculando el intervalo de confianza para la diferencia “(media 2) menos (media 1)”.

De acuerdo, eso es bastante sencillo si lo piensas, pero ahora considera nuestra prueba t que compara la clase de Anastasia con la clase de Bernadette. ¿Cuál debería ser “media 1” y cuál “media 2”?. Es arbitrario. Sin embargo, necesitas designar uno de ellos como “media 1” y el otro como “media 2”. No es sorprendente que la forma en que jamovi maneja esto también sea bastante arbitraria. En versiones anteriores del libro, solía tratar de explicarlo, pero después de un tiempo me di por vencida, porque en realidad no es tan importante y, para ser honesta, nunca puedo acordarme. Cada vez que obtengo un resultado significativo en la prueba t y quiero averiguar cuál es la media más grande, no trato de averiguarlo mirando el estadístico t. ¿Por qué me molestaría en hacer eso? Es una tontería. Es más fácil simplemente mirar las medias del grupo real ya que la salida de jamovi las muestra.

Esto es lo importante. Debido a que realmente no importa lo que te muestre jamovi, generalmente intento informar el estadístico t de tal manera que los números coincidan con el texto. Supongamos que lo que quiero escribir en mi informe es: La clase de Anastasia tuvo calificaciones más altas que la clase de Bernadette. El enunciado aquí implica que el grupo de Anastasia es el primero, por lo que tiene sentido informar del estadístico t como si la clase de Anastasia correspondiera al grupo 1. Si es así, escribiría La clase de Anastasia tuvo calificaciones más altas que la clase de Bernadette $(t(31) = 2.1, p = .04)$.

(En realidad, no subrayaría la palabra “más alto” en la vida real, solo lo hago para enfatizar el punto de que “más alto” corresponde a valores t positivos). Por otro lado, supongamos que la frase que quiero usar tiene la clase de Bernadette en primer lugar. Si es así, tiene más sentido tratar a su clase como el grupo 1, y si es así, la redacción sería así: La clase de Bernadette tenía calificaciones más bajas que la clase de Anastasia $(t(31) = -2.1, p = .04)$.

Debido a que estoy hablando de un grupo que tiene puntuaciones “más bajas” esta vez, es más sensato usar la forma negativa del estadístico t. Simplemente hace que se lea de manera más limpia.

Una última cosa: ten en cuenta que no puedes hacer esto para otros tipos de pruebas estadísticas. Funciona para las pruebas t, pero no tendría sentido para las pruebas de ji-cuadrado, las pruebas F o, de hecho, para la mayoría de las pruebas de las que hablo en este libro. Así que no generalices demasiado este consejo. Solo estoy hablando de pruebas t y nada más.

11.4.3 Supuestos de la prueba

Como siempre, la prueba de hipótesis se basa en algunos supuestos. Para la prueba t de Student hay tres supuestos, algunos de los cuales vimos anteriormente en el contexto de la prueba t de una muestra (consulta Supuestos de la prueba t de una muestra):

Normalidad. Al igual que la prueba t de una muestra, se supone que los datos se distribuyen normalmente. Específicamente, asumimos que ambos grupos están normalmente distribuidos¹⁴. En la sección sobre [Comprobación de la normalidad de una muestra], analizaremos cómo probar la normalidad, y en [Prueba de datos no normales], analizaremos las posibles soluciones.
Independencia. Una vez más, se supone que las observaciones se muestrean de forma independiente. En el contexto de la prueba de Student, esto se refiere a dos aspectos. En primer lugar, suponemos que las observaciones dentro de cada muestra son independientes entre sí (exactamente lo mismo que para la prueba de una muestra). Sin embargo, también asumimos que no hay dependencias entre muestras. Si, por ejemplo, resulta que incluiste a algunos participantes en ambas condiciones experimentales del estudio (por ejemplo, al permitir accidentalmente que la misma persona se inscribiera en diferentes condiciones), entonces hay algunas dependencias de muestras cruzadas que necesitarías tener en cuenta.
Homogeneidad de varianzas (también llamada “homocedasticidad”). El tercer supuesto es que la desviación estándar de la población es la misma en ambos grupos. Se Puede probar este supuesto usando la prueba de Levene, de la que hablaré más adelante en el libro (en Section 13.6.1). Sin embargo, hay una solución muy simple para este supuesto, de la cual hablaré en la siguiente sección.

11.5 La prueba t de muestras independientes (prueba de Welch) {##sec-the-independent-samples-t-test-welch-test}

El mayor problema con el uso de la prueba de Student en la práctica es el tercer supuesto enumerado en la sección anterior. Se supone que ambos grupos tienen la misma desviación estándar. Esto rara vez es cierto en la vida real. Si dos muestras no tienen las mismas medias, ¿por qué deberíamos esperar que tengan la misma desviación estándar? Realmente no hay razón para esperar que este supuesto sea cierto. Más adelante hablaremos de cómo se puede verificar este supuesto, ya que aparece en varios lugares, no solo en la prueba t. Pero ahora hablaré sobre una forma diferente de la prueba t [@ Welch1947] que no se basa en este supuesto. En Figure 11.10 se muestra una ilustración gráfica de lo que asume la prueba t de Welch sobre los datos, para proporcionar un contraste con la versión de la prueba de Student en Figure 11.8. Admito que es un poco extraño hablar sobre la cura antes de hablar sobre el diagnóstico, pero da la casualidad de que la prueba de Welch se puede especificar como una de las opciones de ‘Prueba T de muestras independientes’ en jamovi, así que éste es probablemente el mejor lugar para hablar de ello.

Figure 11.10: Ilustración gráfica de las hipótesis nula y alternativa asumidas por la prueba t de Welch. Al igual que la prueba de Student (Figure 11.9), asumimos que ambas muestras se extraen de una población normal; pero la hipótesis alternativa ya no requiere que las dos poblaciones tengan la misma varianza

La prueba de Welch es muy similar a la prueba de Student. Por ejemplo, el estadístico t que usamos en la prueba de Welch se calcula de la misma manera que para la prueba de Student. Es decir, calculamos la diferencia entre las medias muestrales y luego la dividimos por alguna estimación del error estándar de esa diferencia.

\[t=\frac{\bar{X}_1-\bar{X}_2}{SE(\bar{X}_1-\bar{X}_2)}\]

La principal diferencia es que los cálculos del error estándar son diferentes. Si las dos poblaciones tienen diferentes desviaciones estándar, entonces es una tontería tratar de calcular una estimación de la desviación estándar agrupada, porque está promediando manzanas y naranjas.¹⁵

[Detalle técnico adicional ¹⁶]

La segunda diferencia entre Welch y Student es que los grados de libertad se calculan de forma muy diferente. En la prueba de Welch, los “grados de libertad” ya no tienen que ser un número entero, y no se corresponde del todo con la heurística “número de puntos de datos menos el número de restricciones” que he estado utilizando ahora.

11.5.1 Haciendo la prueba de Welch en jamovi

Si marcas la casilla de verificación de la prueba de Welch en el análisis que hicimos anteriormente, esto es lo que te da (Figure 11.11).

Figure 11.11: resultados que muestran la prueba de Welch junto con la prueba t de Student predeterminada en jamovi

La interpretación de esta salida debería ser bastante obvia. Lee el resultado de la prueba de Welch de la misma manera que lo harías con la prueba de Student. Tienes tus estadísticos descriptivos, los resultados de las pruebas y alguna otra información. Así que todo eso es bastante fácil.

Excepto, excepto… nuestro resultado ya no es significativo. Cuando ejecutamos la prueba de Student, obtuvimos un efecto significativo, pero la prueba de Welch en el mismo conjunto de datos no lo es $(t(23.02) = 2.03, p = .054)$. ¿Qué significa esto? ¿Debería cundir el pánico? Probablemente no. El hecho de que una prueba sea significativa y la otra no, no significa gran cosa, sobre todo porque he manipulado los datos para que esto sucediera. Como regla general, no es una buena idea esforzarse por intentar interpretar o explicar la diferencia entre un valor p de $ 0,049 y un valor p de $ 0,051. Si esto sucede en la vida real, la diferencia en estos valores p se debe casi con seguridad al azar. Lo que importa es que tengas un poco de cuidado al pensar qué prueba usas. La prueba de Student y la prueba de Welch tienen diferentes fortalezas y debilidades. Si las dos poblaciones realmente tienen varianzas iguales, entonces la prueba de Student es un poco más potente (menor tasa de error de tipo II) que la prueba de Welch. Sin embargo, si no tienen las mismas varianzas, entonces se violan los supuestos de la prueba de Student y es posible que no puedas confiar en ella; podrías terminar con una tasa de error Tipo I más alta. Así que es un intercambio. Sin embargo, en la vida real tiendo a preferir la prueba de Welch, porque casi nadie cree que las varianzas de la población sean idénticas.

11.5.2 Supuestos de la prueba

Los supuestos de la prueba de Welch son muy similares a los realizados por la prueba t de Student (ver Supuestos de la prueba, excepto que la prueba de Welch no asume homogeneidad de varianzas. Esto deja solo el supuesto de normalidad y el supuesto de independencia. Los detalles de estos supuestos son los mismos para la prueba de Welch que para la prueba de Student.

11.6 La prueba t de muestras pareadas

Independientemente de si estamos hablando de la prueba de Student o la prueba de Welch, una prueba t de muestras independientes está diseñada para usarse en una situación en la que tienes dos muestras que son, bueno, independientes entre sí. Esta situación surge naturalmente cuando los participantes se asignan aleatoriamente a una de dos condiciones experimentales, pero proporciona una aproximación muy pobre a otros tipos de diseños de investigación. En particular, un diseño de medidas repetidas, en el que se mide a cada participante (con respecto a la misma variable de resultado) en ambas condiciones experimentales, no es adecuado para el análisis mediante pruebas t de muestras independientes. Por ejemplo, podríamos estar interesadas en saber si escuchar música reduce la capacidad de la memoria de trabajo de las personas. Con ese fin, podríamos medir la capacidad de la memoria de trabajo de cada persona en dos condiciones: con música y sin música. En un diseño experimental como este, ¹⁷ cada participante aparece en ambos grupos. Esto requiere que abordemos el problema de una manera diferente, usando la prueba t de muestras pareadas.

11.6.1 Los datos

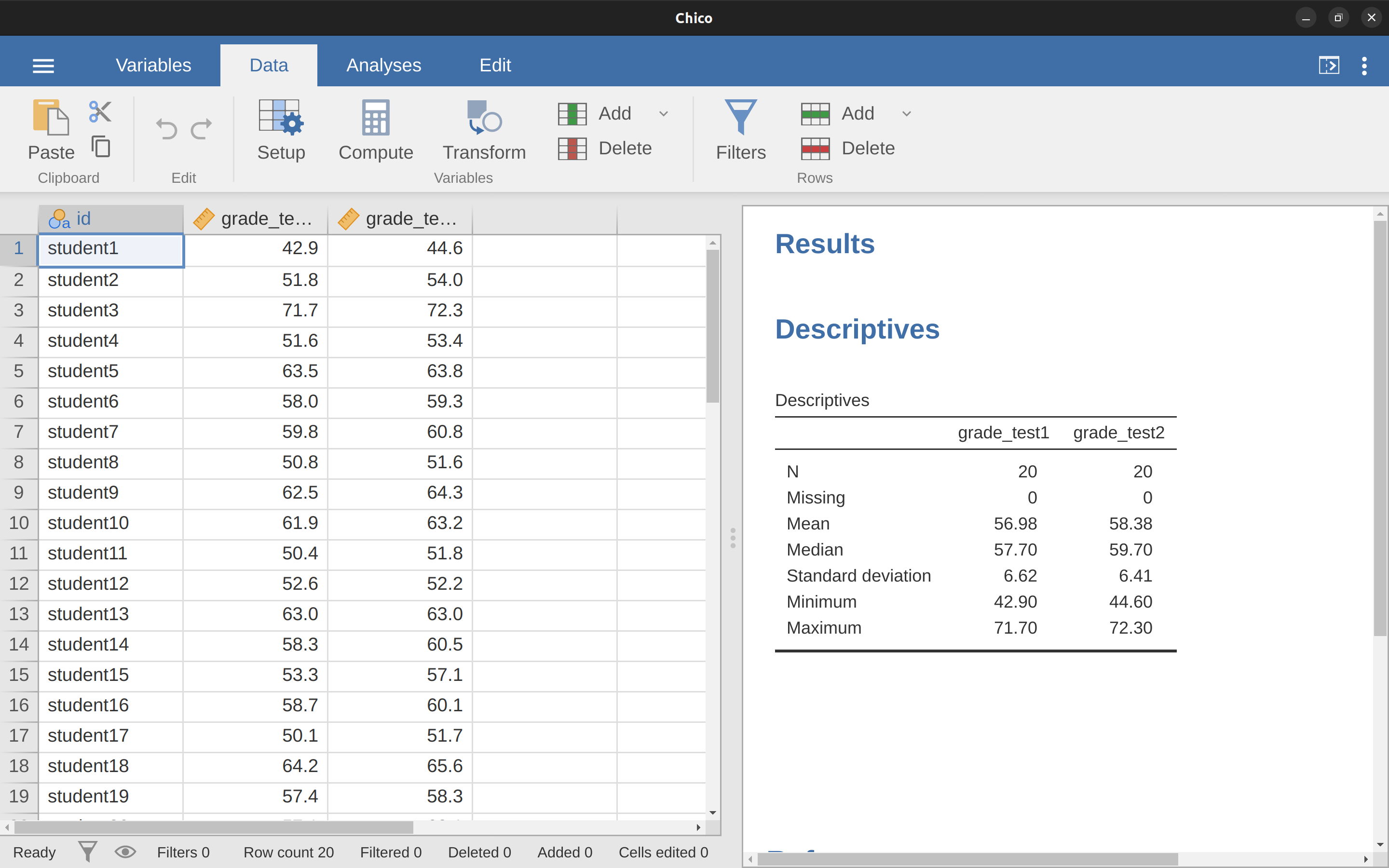
El conjunto de datos que usaremos esta vez proviene de la clase de la Dra. Chico.¹⁸ En su clase, los estudiantes realizan dos pruebas importantes, una al principio del semestre y otra más tarde. Por lo que cuenta, ella dirige una clase muy dura, que la mayoría de los estudiantes consideran un gran reto. Pero ella argumenta que al establecer evaluaciones difíciles, se alienta a los estudiantes a trabajar más duro. Su teoría es que la primera prueba es un poco como una “llamada de atención” para los estudiantes. Cuando se den cuenta de lo difícil que es realmente su clase, trabajarán más duro para la segunda prueba y obtendrán una mejor calificación. ¿Tiene razón? Para probar esto, importemos el archivo chico.csv a jamovi. Esta vez jamovi hace un buen trabajo durante la importación de atribuir correctamente los niveles de medida. El conjunto de datos chico contiene tres variables: una variable id que identifica a cada estudiante en la clase, la variable grade_test1 que registra la calificación del estudiante para la primera prueba y la variable grade_test2 que tiene las calificaciones para la segunda prueba.

Si miramos la hoja de cálculo de jamovi, parece que la clase es difícil (la mayoría de las calificaciones están entre 50% y 60%), pero parece que hay una mejora desde la primera prueba hasta la segunda.

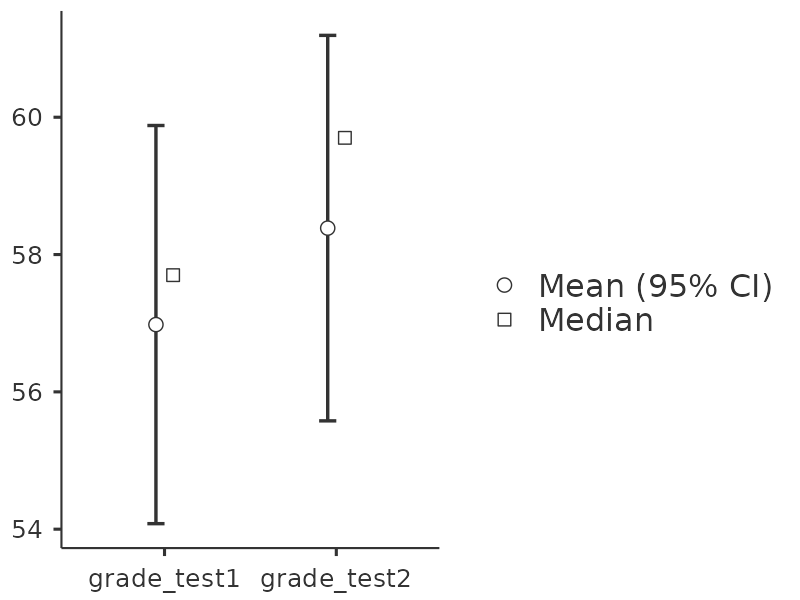
Si echamos un vistazo rápido a los estadísticos descriptivos, en Figure 11.12, vemos que esta impresión parece confirmarse. Entre los 20 estudiantes, la calificación media para la primera prueba es del 57 %, pero aumenta al 58 % para la segunda prueba. Aunque, dado que las desviaciones estándar son 6,6 % y 6,4 % respectivamente, se empieza a sentir que tal vez la mejora es simplemente ilusoria; tal vez solo una variación aleatoria. Esta impresión se refuerza cuando ves las medias y los intervalos de confianza trazados en Figure 11.13 (a). Si nos basáramos únicamente en este gráfico y observáramos la amplitud de esos intervalos de confianza, tendríamos la tentación de pensar que la aparente mejora del rendimiento de los estudiantes es pura casualidad.

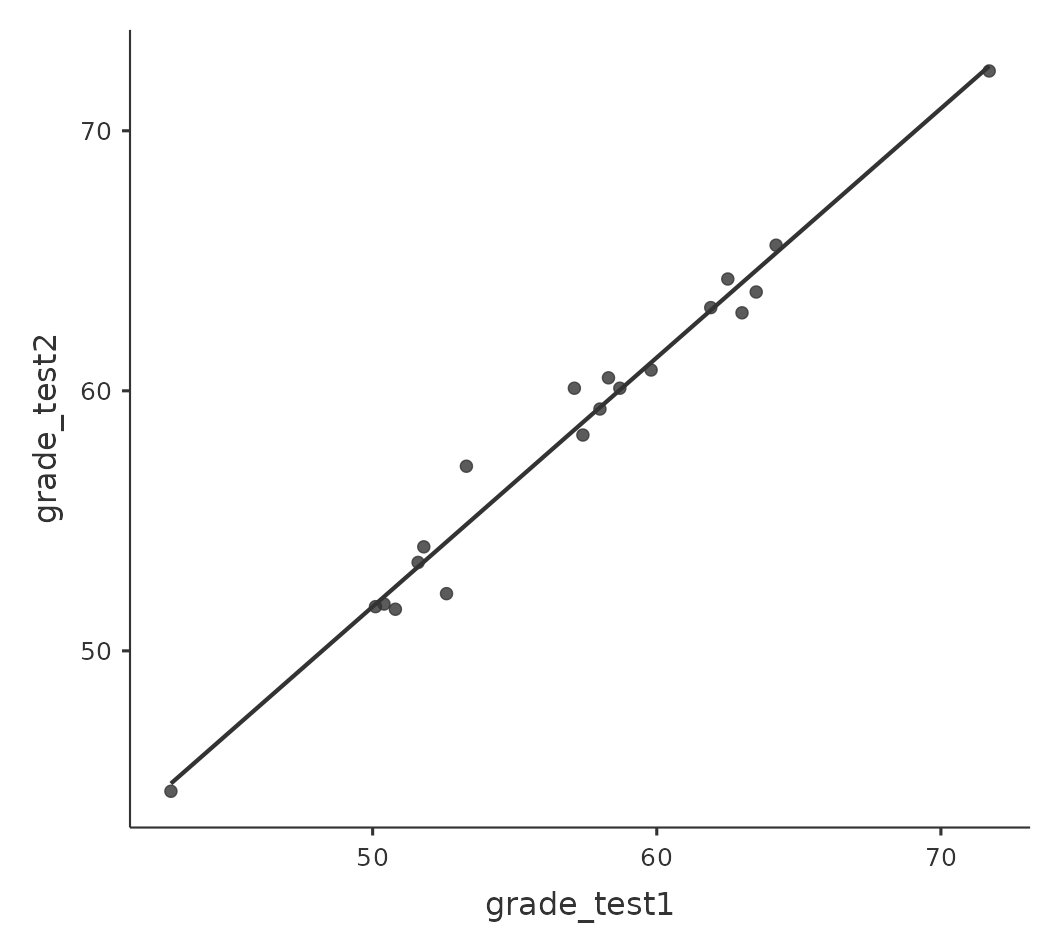
Figure 11.12: descriptivos para las dos variables de prueba de grado en el conjunto de datos de chico

Sin embargo, esta impresión es incorrecta. Para ver por qué, echa un vistazo al gráfico de dispersión de las calificaciones de la prueba 1 frente a las calificaciones de la prueba 2, que se muestra en Figure 11.13 (b). En este gráfico, cada punto corresponde a las dos calificaciones de un estudiante determinado. Si su calificación para la prueba 1 (coordenada x) es igual a su calificación para la prueba 2 (coordenada y), entonces el punto cae en la línea. Los puntos que caen por encima de la línea son los estudiantes que tuvieron mejor rendimiento en la segunda prueba. Desde un punto de vista crítico, casi todos los puntos de datos se sitúan por encima de la línea diagonal: casi todos los estudiantes parecen haber mejorado su calificación, aunque solo sea un poco. Esto sugiere que deberíamos observar la mejora realizada por cada estudiante de una prueba a la siguiente y tratarla como nuestros datos brutos. Para hacer esto, necesitaremos crear una nueva variable para la mejora que hace cada estudiante y agregarla al conjunto de datos de chico. La forma más sencilla de hacer esto es calcular una nueva variable, con la expresión calificación prueba2 - calificación prueba1.

Una vez que hayamos calculado esta nueva variable de mejora, podemos dibujar un histograma que muestre la distribución de estas puntuaciones de mejora, que se muestra en Figure 11.14. Si nos fijamos en el histograma, está muy claro que hay una mejora real aquí. La gran mayoría de los estudiantes obtuvo una puntuación más alta en la prueba 2 que en la prueba 1, lo que se refleja en el hecho de que casi todo el histograma está por encima de cero.

Figure 11.14: Histograma que muestra la mejora realizada por cada estudiante en la clase del Dr. Chico. Ten en cuenta que casi toda la distribución está por encima de cero: la gran mayoría de los estudiantes mejoraron su rendimiento des la primera prueba a la segunda

11.6.2 ¿Qué es la prueba t de muestras pareadas?

A la luz de la exploración anterior, pensemos en cómo construir una prueba t apropiada. Una posibilidad sería intentar ejecutar una prueba t de muestras independientes utilizando grade_test1 y grade_test2 como las variables de interés. Sin embargo, esto es claramente lo incorrecto, ya que la prueba t de muestras independientes asume que no existe una relación particular entre las dos muestras. Sin embargo, está claro que esto no es cierto en este caso debido a la estructura de medidas repetidas de los datos. Para usar el lenguaje que introduje en la última sección, si intentáramos hacer una prueba t de muestras independientes, estaríamos fusionando las diferencias dentro del sujeto (que es lo que nos interesa probar) con la variabilidad entre sujetos (que no nos interesa).

La solución al problema es obvia, espero, ya que ya hicimos todo el trabajo duro en la sección anterior. En lugar de ejecutar una prueba t de muestras independientes en grade_test1 y grade_test2, ejecutamos una prueba t de una muestra en la variable de diferencia dentro del sujeto, mejora. Para formalizar esto un poco, si $X_{i1}$ es la puntuación que obtuvo el i-ésimo participante en la primera variable, y $X_{i2}$ es la puntuación que obtuvo la misma persona en la segunda, entonces la puntuación de diferencia es:

\[D_i=X_{i1}-X_{i2}\]

Ten en cuenta que las puntuaciones de diferencia son la variable 1 menos la variable 2 y no al revés, por lo que si queremos que la mejora corresponda a una diferencia de valor positivo, en realidad queremos que la “prueba 2” sea nuestra “variable 1”. Igualmente, diríamos que $\mu_D = \mu_1 - \mu_2$ es la media poblacional para esta variable diferencia. Entonces, para convertir esto en una prueba de hipótesis, nuestra hipótesis nula es que esta diferencia de medias es cero y la hipótesis alternativa es que no lo es.

\[H_0:\mu_D=0\] \[H_1:\mu_D \neq 0\]

Asumiendo que estamos hablando de una prueba bilateral. Esto es más o menos idéntico a la forma en que describimos las hipótesis para la prueba t de una muestra. La única diferencia es que el valor específico que predice la hipótesis nula es 0. Por lo tanto, nuestro estadístico t también se define más o menos de la misma manera. Si hacemos que $\bar{D}$ denote la media de las puntuaciones de diferencia, entonces

\[t=\frac{\bar{D}}{SE(\bar{D})}\]

que es

\[t=\frac{\bar{D}}{\frac{\hat{\sigma} _D}{\sqrt{N}}}\]

donde $\hat{\sigma}_D$ es la desviación estándar de las puntuaciones de diferencia. Dado que esta es solo una prueba t ordinaria de una muestra, sin nada especial, los grados de libertad siguen siendo $N - 1$. Y eso es todo. La prueba t de muestras pareadas realmente no es una prueba nueva en absoluto. Es una prueba t de una muestra, pero aplicada a la diferencia entre dos variables. En realidad es muy simple. La única razón por la que merece una discusión tan larga como la que acabamos de ver es que debes poder reconocer cuándo una prueba de muestras pareadas es apropiada y comprender por qué es mejor que una prueba t de muestras independientes.

11.6.3 Haciendo la prueba en jamovi

¿Cómo se hace una prueba t de muestras pareadas en jamovi? Una posibilidad es seguir el proceso que describí anteriormente. Es decir, crea una variable de “diferencia” y luego ejecutas una prueba t de una muestra sobre eso. Como ya hemos creado una variable llamada mejora, hagámoslo y veamos qué obtenemos, Figure 11.15.

Figure 11.15: resultados que muestran una prueba t de una muestra en puntajes de diferencia emparejados

El resultado que se muestra en Figure 11.15 tiene (obviamente) el mismo formato que tenía la última vez que usamos el análisis de prueba t de una muestra (Section 11.2), y confirma nuestra intuición. Hay una mejora promedio de $1.4\%$ de la prueba 1 a la prueba 2, y esto es significativamente diferente de $0$ $(t(19) = 6.48, p< .001)$.

Sin embargo, supongamos que eres perezosa y no quieres hacer todo el esfuerzo de crear una nueva variable. O tal vez solo quieras mantener clara la diferencia entre las pruebas de una muestra y muestras pareadas. Si es así, puedes usar el análisis ‘Prueba T de muestras emparejadas’ de jamovi, obteniendo los resultados que se muestran en Figure 11.16.

Figure 11.16: resultados que muestran una prueba t de muestra pareada. Comparar con Figure 11.15

Las cifras son idénticas a las de la prueba de una muestra, lo que, por supuesto, tiene que ser así, dado que la prueba t de muestras pareadas no es más que una prueba de una muestra.

11.7 Pruebas unilaterales

Al presentar la teoría de las pruebas de hipótesis nulas, mencioné que hay algunas situaciones en las que es apropiado especificar una prueba unilateral (ver Section 9.4.3). Hasta ahora, todas las pruebas t han sido pruebas bilaterales. Por ejemplo, cuando especificamos una prueba t de una muestra para las calificaciones en la clase del Dr. Zeppo, la hipótesis nula fue que la verdadera media era $67.5\%$. La hipótesis alternativa era que la verdadera media era mayor o menor que $67.5\%$. Supongamos que solo nos interesa saber si la media real es mayor que $67,5\%$ y no tenemos ningún interés en probar si la media real es menor que $67,5\%$. Si es así, nuestra hipótesis nula sería que la verdadera media es $67,5\%$ o menos, y la hipótesis alternativa sería que la verdadera media es mayor que $67,5\%$. En jamovi, para el análisis ‘Prueba T de una muestra’, puedes especificar esto haciendo clic en la opción ‘$>$ Valor de prueba’, en ‘Hipótesis’. Cuando hayas hecho esto, obtendrás los resultados que se muestran en Figure 11.17.

Figure 11.17: resultados de jamovi que muestran una ‘Prueba T de una muestra’ donde la hipótesis real es unilateral, es decir, que la media real es mayor que $67.5\%$

Ten en cuenta que hay algunos cambios con respecto a la salida que vimos la última vez. Lo más importante es el hecho de que la hipótesis real ha cambiado, para reflejar la prueba diferente. La segunda cosa a tener en cuenta es que aunque el estadístico t y los grados de libertad no han cambiado, el valor p sí lo ha hecho. Esto se debe a que la prueba unilateral tiene una región de rechazo diferente de la prueba bilateral. Si has olvidado por qué es esto y qué significa, puede que te resulte útil volver a leer Chapter 9 y Section 9.4.3 en particular. La tercera cosa a tener en cuenta es que el intervalo de confianza también es diferente: ahora informa un intervalo de confianza “unilateral” en lugar de uno bilateral. En un intervalo de confianza de dos colas, estamos tratando de encontrar los números a y b de modo que estemos seguros de que, si tuviéramos que repetir el estudio muchas veces, entonces $95\%$ del tiempo la media estaría entre a y b. En un intervalo de confianza unilateral, estamos tratando de encontrar un solo número a tal que estemos seguros de que $95\%$ del tiempo la verdadera media sería mayor que a (o menor que a si seleccionaste la Medida 1 < Medida 2 en la sección ‘Hipótesis’).

Así es como se hace una prueba t unilateral de una muestra. Sin embargo, todas las versiones de la prueba t pueden ser unilaterales. Para una prueba t de muestras independientes, podrías tener una prueba unilateral si solo estás interesada en probar si el grupo A tiene puntuaciones más altas que el grupo B, pero no tienes interés en averiguar si el grupo B tiene puntuaciones más altas que el grupo R. Supongamos que, para la clase del Dr. Harpo, quisieras ver si los estudiantes de Anastasia tenían calificaciones más altas que las de Bernadette. Para este análisis, en las opciones de ‘Hipótesis’, especifica que ‘Grupo 1 > Grupo2’. Deberías obtener los resultados que se muestran en Figure 11.18.

Figure 11.18: resultados de jamovi que muestran una ‘Prueba t de muestras independientes’ donde la hipótesis real es unilateral, es decir, que los estudiantes de Anastasia obtuvieron calificaciones más altas que los de Bernadette

Una vez más, la salida cambia de forma predecible. La definición de la hipótesis alternativa ha cambiado, el valor p ha cambiado y ahora informa un intervalo de confianza unilateral en lugar de uno bilateral.

¿Qué pasa con la prueba t de muestras pareadas? Supongamos que quisiéramos probar la hipótesis de que las calificaciones suben de la prueba 1 a la prueba 2 en la clase del Dr. Zeppo y no estamos preparados para considerar la idea de que las calificaciones bajan. En jamovi, harías esto especificando, en la opción ‘Hipótesis’, que grade_test2 (‘Medida 1’ en jamovi, porque copiamos esto primero en el cuadro de pares de variables) > grade test1 (‘Medida 2’ en jamovi). Deberías obtener los resultados que se muestran en Figure 11.19.

Figure 11.19: resultados de jamovi que muestran una ‘Prueba T de muestras emparejadas’ donde la hipótesis real es unilateral, es decir, calificación prueba2 (‘Medida 1’) $>$ calificación prueba1 (‘Medida 2’)

Una vez más, la salida cambia de forma predecible. La hipótesis ha cambiado, el valor p ha cambiado y el intervalo de confianza ahora es unilateral.

11.8 Tamaño del efecto

La medida del tamaño del efecto más utilizada para una prueba t es la d de Cohen (Cohen, 1988). En principio, se trata de una medida muy sencilla, pero que presenta algunos inconvenientes cuando se profundiza en los detalles. El propio Cohen la definió principalmente en el contexto de una prueba t de muestras independientes, específicamente la prueba de Student. En ese contexto, una forma natural de definir el tamaño del efecto es dividir la diferencia entre las medias por una estimación de la desviación estándar. En otras palabras, estamos buscando calcular algo similar a esto:

\[d=\frac{(\text{media 1})-(\text{media 2})}{\text{desviación estándar}}\]

y sugirió una guía aproximada para interpretar $d$ en Table 11.3.

Table 11.3:
Una guía (muy) aproximada para interpretar la d de Cohen. Mi recomendación personal es no usarlos a ciegas. El estadístico d tiene una interpretación natural en sí mismo. Vuelve a describir la diferencia de medias como el número de desviaciones estándar que separa esas medias. Por lo tanto, generalmente es una buena idea pensar en lo que eso significa en términos prácticos. En algunos contextos, un efecto ‘pequeño’ podría ser de gran importancia práctica. En otras situaciones, un efecto ‘grande’ puede no ser tan interesante
d-value	rough interpretation
about 0.2	"small" effect
about 0.5	"moderate" effect
about 0.8	"large" effect

Se podría pensar que no hay ninguna ambigüedad, pero no es así. Esto se debe en gran parte a que Cohen no fue demasiado específico sobre lo que pensó que debería usarse como la medida de la desviación estándar (en su defensa, estaba tratando de hacer un punto más amplio en su libro, no criticar los pequeños detalles). Como comenta @ McGrath2006, hay varias versiones diferentes de uso común, y cada autor tiende a adoptar una notación ligeramente diferente. En aras de la simplicidad (en oposición a la precisión), usaré d para referirme a cualquier estadístico que calcule a partir de la muestra, y usaré $\delta$ para referirme a un teórico efecto poblacional. Obviamente, eso significa que hay varias cosas diferentes, todas llamadas d.

Mi sospecha es que el único momento en el que querrías la d de Cohen es cuando estás ejecutando una prueba t, y jamovi tiene una opción para calcular el tamaño del efecto para todos los diferentes tipos de prueba t que proporciona.

11.8.1 d de Cohen de una muestra

La situación más sencilla de considerar es la correspondiente a una prueba t de una muestra. En este caso, se trata de una media muestral $\bar{X}$ y una media poblacional (hipotética) $\mu_0$ con la que compararla. No solo eso, en realidad solo hay una forma sensata de estimar la desviación estándar de la población. Simplemente usamos nuestra estimación habitual $\hat{\sigma}$. Por lo tanto, terminamos con la siguiente como la única forma de calcular $d$

\[d=\frac{\bar{X}-\mu_0}{\hat{\sigma}}\]

Cuando volvemos a mirar los resultados en Figure 11.6, el valor del tamaño del efecto es $d = 0,50$ de Cohen. Entonces, en general, los estudiantes de psicología de la clase del Dr. Zeppo obtienen calificaciones ($media = 72,3\%$) que son alrededor de 0,5 desviaciones estándar más altas que el nivel que esperarías ($67,5\%$) si tuvieran un rendimiento igual que otros estudiantes. A juzgar por la guía aproximada de Cohen, este es un tamaño de efecto moderado.

11.8.2 d de Cohen a partir de una prueba t de Student

La mayoría de los debates sobre la $d$ de Cohen se centran en una situación que es análoga a la prueba t de Student de muestras independientes, y es en este contexto que la historia se vuelve más complicada, ya que hay varias versiones diferentes de $d$ que es posible que quieras utilizar en esta situación. Para entender por qué hay múltiples versiones de $d$, es útil tomarse el tiempo para escribir una fórmula que corresponda al verdadero tamaño del efecto poblacional $\delta$. Es bastante sencilla,

\[\delta=\frac{\mu_1-\mu_2}{\sigma}\]

donde, como es habitual, $\mu_1$ y $\mu_2$ son las medias poblacionales correspondientes al grupo 1 y al grupo 2 respectivamente, y $\sigma$ es la desviación estándar (igual para ambas poblaciones). La forma obvia de estimar $\delta$ es hacer exactamente lo mismo que hicimos en la prueba t, es decir, usar las medias muestrales como la línea superior y una desviación estándar combinada para la línea inferior.

\[d=\frac{\bar{X}_1-\bar{X}_2}{\hat{\sigma}_p}\]

donde $\hat{\sigma}_p$ es exactamente la misma medida de desviación estándar agrupada que aparece en la prueba t. Esta es la versión más utilizada de la d de Cohen cuando se aplica al resultado de una prueba t de Student, y es la que se proporciona en jamovi. A veces se la denomina estadístico $g$ de Hedges (Hedges, 1981).

Sin embargo, hay otras posibilidades que describiré brevemente. En primer lugar, es posible que tengas razones para querer usar solo uno de los dos grupos como base para calcular la desviación estándar. Este enfoque (a menudo llamado $\triangle$ de Glass, pronunciado delta) solo tiene sentido cuando tienes una buena razón para tratar a uno de los dos grupos como un reflejo más puro de la “variación natural” del otro. Esto puede suceder si, por ejemplo, uno de los dos grupos es un grupo de control. En segundo lugar, recuerda que en el cálculo habitual de la desviación estándar agrupada dividimos entre $N - 2$ para corregir el sesgo en la varianza de la muestra. En una versión de la d de Cohen se omite esta corrección y en su lugar se divide por $N$. Esta versión tiene sentido principalmente cuando intentas calcular el tamaño del efecto muestral en lugar de estimar el tamaño del efecto poblacional. Finalmente, hay una versión llamada g de Hedge, basada en Hedges & Olkin (1985), que señala que existe un pequeño sesgo en la estimación habitual (agrupada) para la d de Cohen.¹⁹

En cualquier caso, ignorando todas aquellas variaciones que podrías utilizar si quisieras, echemos un vistazo a la versión por defecto en jamovi. En Figure 11.10 la de de Cohen es $d = 0.74$, lo que indica que las calificaciones de los estudiantes en la clase de Anastasia son, en promedio, $0.74$ desviaciones estándar más altas que las calificaciones de los estudiantes en la clase de Bernadette. Para una prueba de Welch, el tamaño del efecto estimado es el mismo (Figure 11.12).

11.8.3 d de Cohen a partir de una prueba de muestras pareadas

Finalmente, ¿qué debemos hacer para una prueba t de muestras pareadas? En este caso, la respuesta depende de lo que estés tratando de hacer. jamovi asume que deseas medir los tamaños de su efecto en relación con la distribución de las puntuaciones de diferencia, y la medida de d que calcula es:

\[d=\frac{\bar{D}}{\hat{\sigma}_D}\]

donde $\hat{\sigma}_D$ es la estimación de la desviación estándar de las diferencias. En Figure 11.16 la de de Cohen es $d = 1,45$, lo que indica que las puntuaciones de la calificación en el momento 2 son, en promedio, $1,45$ desviaciones estándar más altas que las puntuaciones de la calificación en el momento 1.

Esta es la versión de $d$ de Cohen que se informa en el análisis ‘Prueba T de muestras emparejadas’ de jamovi. La única pega es averiguar si esta es la medida que deseas o no. En la medida en que te importen las consecuencias prácticas de tu investigación, a menudo querrás medir el tamaño del efecto en relación con las variables originales, no las puntuaciones de diferencia (p. ej., la mejora del 1% en la clase del Dr. Chico con el tiempo es bastante pequeña cuando se compara con la cantidad de variación entre estudiantes en las calificaciones), en cuyo caso usa las mismas versiones de la d de Cohen que usarías para una prueba de Student o Welch. No es tan sencillo hacer esto en jamovi; básicamente, debes cambiar la estructura de los datos en la vista de hoja de cálculo, por lo que no entraré en eso aquí ²⁰, pero la d de Cohen para esta situación es bastante diferente: es $ 0.22 $ que es bastante pequeña cuando se evalúa en la escala de las variables originales.

11.9 Comprobando la normalidad de una muestra

Todas las pruebas que hemos discutido hasta ahora en este capítulo han asumido que los datos están normalmente distribuidos. Este supuesto suele ser bastante razonable, porque el teorema cntral del límite (ver Section 8.3.3) tiende a garantizar que muchas cantidades del mundo real se distribuyan normalmente. Cada vez que sospeches que tu variable es en realidad un promedio de muchas cosas diferentes, existe una gran probabilidad de que se distribuya normalmente, o al menos lo suficientemente cerca de lo normal como para que puedas usar pruebas t. Sin embargo, la vida no viene con garantías y, además, hay muchas formas en las que puedes terminar con variables que son muy anormales. Por ejemplo, cada vez que pienses que tu variable es en realidad el mínimo de muchas cosas diferentes, es muy probable que termine bastante sesgada. En psicología, los datos de tiempo de respuesta (TR) son un buen ejemplo de esto. Si supones que hay muchas cosas que podrían desencadenar una respuesta de un participante humano, entonces la respuesta real ocurrirá la primera vez que ocurra uno de estos eventos desencadenantes.²¹ Esto significa que los datos de TR son sistemáticamente no normales. De acuerdo, entonces, si todas las pruebas asumen la normalidad, y la mayor parte, pero no siempre, la satisfacen (al menos aproximadamente) los datos del mundo real, ¿cómo podemos verificar la normalidad de una muestra? En esta sección analizo dos métodos: gráficos QQ y la prueba de Shapiro-Wilk.

11.9.1 Gráficos QQ

Una forma de verificar si una muestra viola el supuesto de normalidad es dibujar un “Gráfico QQ” (Gráfico Cuantil-Cuantil). Esto te permite verificar visualmente si estás viendo alguna infracción sistemática. En un gráfico QQ, cada observación se representa como un solo punto. La coordenada x es el cuantil teórico en el que debería caer la observación si los datos se distribuyeran normalmente (con la media y la varianza estimadas a partir de la muestra), y en la coordenada y está el cuantil real de los datos dentro de la muestra. Si los datos son normales, los puntos deben formar una línea recta. Por ejemplo, veamos qué sucede si generamos datos tomando muestras de una distribución normal y luego dibujando un gráfico QQ. Los resultados se muestran en Figure 11.20.

Figure 11.20: Histograma (panel (a)) y gráfico QQ normal (panel (b)) de normal.data, una muestra distribuida normalmente con $100$ observaciones. El estadístico de Shapiro-Wilk asociado con estos datos es $W = .99$, lo que indica que no se detectaron desviaciones significativas de la normalidad ($p = .54)$

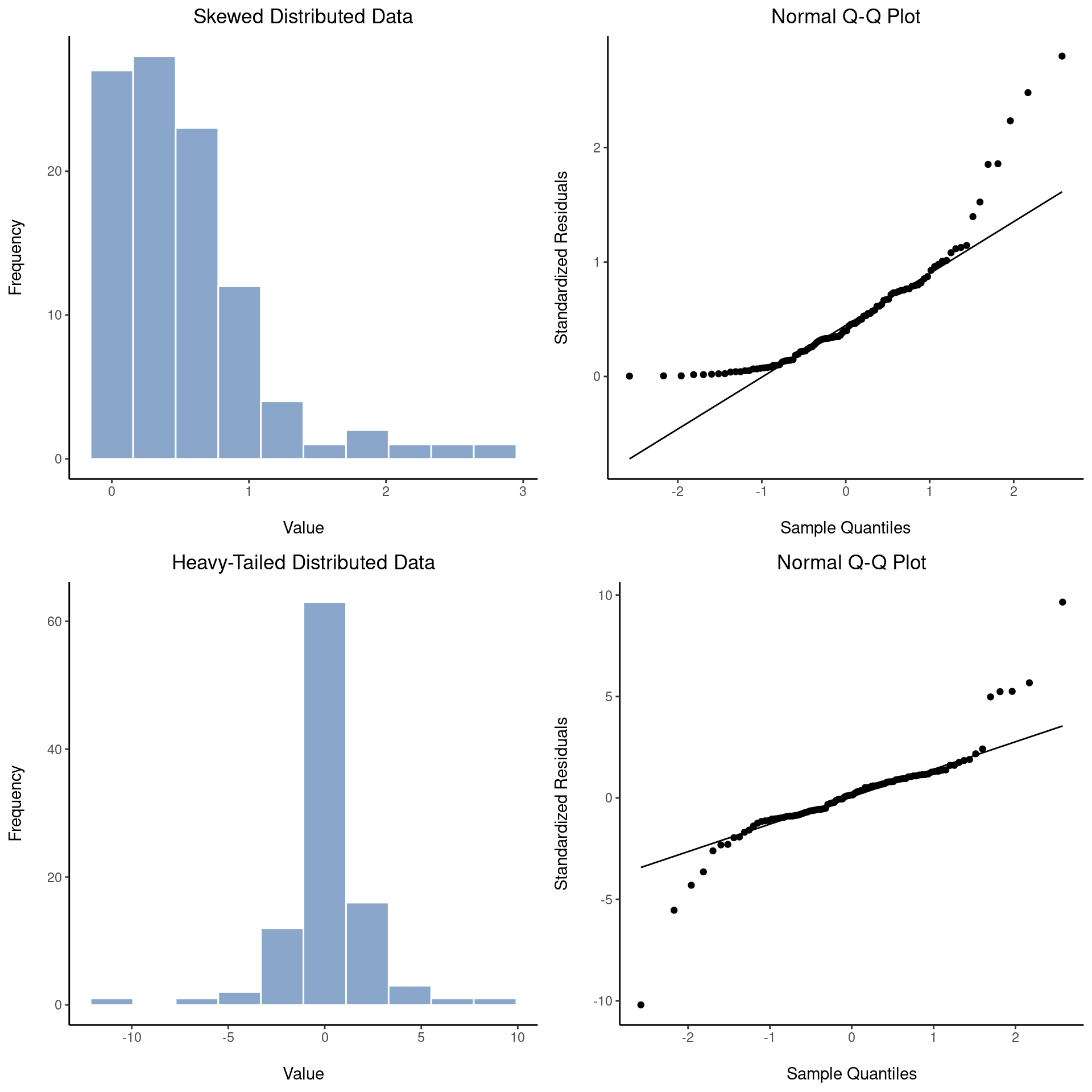
Como puedes ver, estos datos forman una línea bastante recta; ¡lo cual no es una sorpresa dado que los cogimos como muestra de una distribución normal! Por el contrario, echa un vistazo a los dos conjuntos de datos que se muestran en Figure 11.21. Los paneles superiores muestran el histograma y un gráfico QQ para un conjunto de datos que está muy sesgado: el gráfico QQ se curva hacia arriba. Los paneles inferiores muestran los mismos gráficos para un conjunto de datos de cola pesada (es decir, alta curtosis): en este caso, el gráfico QQ se aplana en el medio y se curva bruscamente en cada extremo.

Figure 11.21: en la fila superior, un histograma y un gráfico QQ normal de las observaciones de $100$ en un conjunto de datos sesgados. La asimetría de los datos aquí es de $1.88$ y se refleja en un gráfico QQ que se curva hacia arriba. Como consecuencia, el estadístico de Shapiro-Wilk es $W = .80$, lo que refleja una desviación significativa de la normalidad ($p< .001$). La fila inferior muestra los mismos gráficos para un conjunto de datos de cola pesada, que nuevamente consta de 100 observaciones. En este caso, las colas pesadas en los datos producen una curtosis alta ($ 6,57 $) y hacen que el gráfico QQ se aplane en el medio y se curve bruscamente a ambos lados. El estadístico resultante de Shapiro-Wilk es $W = .75$, lo que nuevamente refleja una falta de normalidad significativa ($p<.001)$

11.9.2 Gráficos QQ para pruebas t independientes y pareadas

En nuestros análisis anteriores mostramos cómo realizar en jamovi una prueba t independiente (Figure 11.10) y una prueba t de muestras pareadas (Figure 11.16). Y para estos análisis, jamovi proporciona una opción para mostrar un gráfico QQ para las puntuaciones de diferencia (que jamovi llama “residuales”), que es una mejor manera de verificar el supuesto de normalidad. Cuando seleccionamos esta opción para estos análisis, obtenemos los gráficos QQ que se muestran en Figure 11.22 y Figure 11.23, respectivamente. Mi interpretación es que estos gráficos muestran que las puntuaciones de diferencia están razonablemente distribuidas normalmente, ¡así que estamos listos para comenzar!

Figure 11.22: diagrama QQ para el análisis de prueba t independiente que se muestra en Figure 11.10

Figure 11.23: gráfico QQ para el análisis de prueba t de muestras emparejadas que se muestra en Figure 11.16

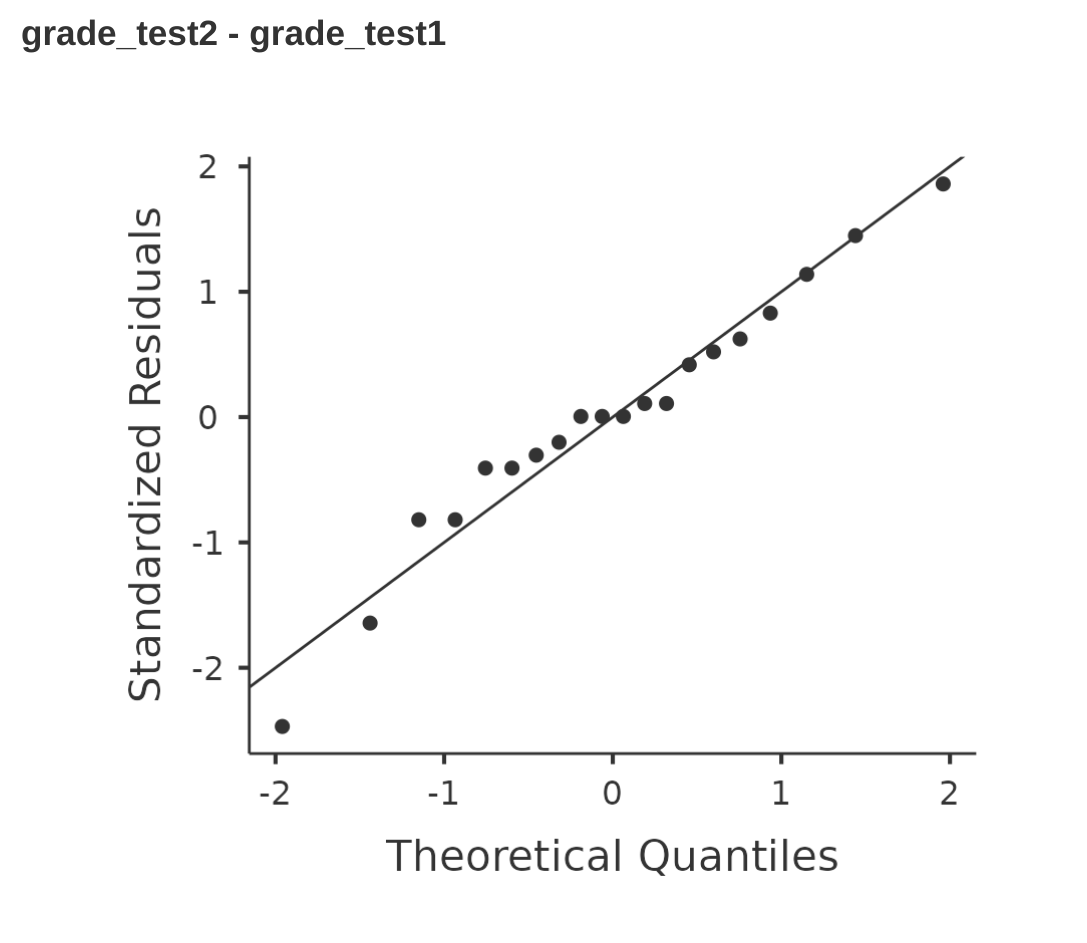
11.9.3 Pruebas de Shapiro-Wilk

Los diagramas QQ ofrecen una buena manera de verificar informalmente la normalidad de tus datos, pero a veces querrás hacer algo un poco más formal y la prueba de Shapiro-Wilk [@ Shapiro1965] es probablemente lo que estás buscando .²² Como era de esperar, la hipótesis nula que se prueba es que un conjunto de $N$ observaciones se distribuye normalmente.

[Detalle técnico adicional ²³]

Figure 11.24: Distribución muestral del estadístico $W$ de Shapiro-Wilk, bajo la hipótesis nula de que los datos se distribuyen normalmente, para muestras de tamaño 10, 20 y 50. Nótese que valores pequeños de $W$ indican desviación de la normalidad

Para obtener el estadístico de Shapiro-Wilk en las pruebas t de jamovi, marca la opción de ‘Normalidad’ que se encuentra en ‘Supuestos’. En los datos muestreados aleatoriamente ($N = 100$) que usamos para el gráfico QQ, el valor del estadístico de la prueba de normalidad de Shapiro-Wilk fue $W = 0,99$ con un valor p de $0,54$. Entonces, como es lógico, no tenemos evidencia de que estos datos se aparten de la normalidad. Al informar los resultados de una prueba de Shapiro-Wilk, debes (como de costumbre) asegurarte de incluir la prueba estadística $W$ y el valor p, aunque dado que la distribución muestral depende tanto de $N$, probablemente estaría bien incluir $N$ también.

11.9.4 Ejemplo

Mientras tanto, probablemente valga la pena mostrarte un ejemplo de lo que sucede con el gráfico QQ y la prueba de Shapiro-Wilk cuando los datos no son normales. Para eso, veamos la distribución de nuestros datos de márgenes ganadores de la AFL, que si recuerdas Chapter 4, no parecían provenir de una distribución normal en absoluto. Esto es lo que sucede con el gráfico QQ (Figure 11.25).

Figure 11.25: gráfico QQ que muestra la no normalidad de los datos de márgenes ganadores de la AFL

Y cuando ejecutamos la prueba de Shapiro-Wilk en los datos de márgenes de AFL, obtenemos un valor para la prueba estadística de normalidad de Shapiro-Wilk de $W = 0.94$ y valor p = $9.481$x$10^{-07}$. ¡Claramente un efecto significativo!

11.10 Comprobación de datos no normales

Bien, supongamos que los datos resultan ser sustancialmente no normales, pero aún así queremos ejecutar algo como una prueba t. Esta situación se da a menudo en la vida real. Para los datos de los márgenes ganadores de la AFL, por ejemplo, la prueba de Shapiro-Wilk dejó muy claro que se viola el supuesto de normalidad. Esta es la situación en la que conviene utilizar las pruebas de Wilcoxon.

Al igual que la prueba t, la prueba de Wilcoxon viene en dos formas, de una muestra y de dos muestras, y se utilizan más o menos en las mismas situaciones que las pruebas t correspondientes. A diferencia de la prueba t, la prueba de Wilcoxon no asume normalidad, lo cual es bueno. De hecho, no hace ninguna suposición sobre qué tipo de distribución está involucrada. En la jerga estadística, esto lo convierte en pruebas no paramétricas. Aunque evitar el supuesto de normalidad es bueno, existe un inconveniente: la prueba de Wilcoxon suele ser menos potente que la prueba t (es decir, una mayor tasa de error de tipo II). No discutiré las pruebas de Wilcoxon con tanto detalle como las pruebas t, pero os daré una breve descripción general.

11.10.1 Prueba U de Mann-Whitney de dos muestras

Comenzaré describiendo la prueba U de Mann-Whitney, ya que en realidad es más simple que la versión de una muestra. Supongamos que estamos viendo las puntuaciones de 10 personas en algún examen. Como mi imaginación ahora me ha fallado por completo, supongamos que es una “prueba de asombro” y que hay dos grupos de personas, “A” y “B”. Tengo curiosidad por saber qué grupo es más impresionante. Los datos están incluidos en el archivo awesome.csv, y hay dos variables además de la variable ID habitual: puntuaciones y grupo.

Mientras no haya vínculos (es decir, personas con exactamente la misma puntuación de genialidad), la prueba que queremos hacer es muy simple. Todo lo que tenemos que hacer es construir una tabla que compare cada observación del grupo A con cada observación del grupo B. Siempre que el dato del grupo A sea más grande, colocamos una marca de verificación en la tabla (Table 11.4).

Table 11.4:
Comparación de observaciones por grupo para una prueba U de Mann-Whitney de dos muestras
		group B
		14.5	10.4	12.4	11.7	13.0
group A	6.4	.	.	.	.	.
	10.7	.	$ \checkmark $	.	.	.
	11.9	.	$ \checkmark $	.	$ \checkmark $	.
	7.3	.	.	.	.	.
	10	.	.	.	.	.

Luego contamos el número de marcas de verificación. Esta es nuestra prueba estadística, W. ²⁴ La distribución muestral real para W es algo complicada y me saltearé los detalles. Para nuestros propósitos, es suficiente notar que la interpretación de W es cualitativamente la misma que la interpretación de $t$ o $z$. Es decir, si queremos una prueba bilateral, rechazamos la hipótesis nula cuando W es muy grande o muy pequeño, pero si tenemos una hipótesis unidireccional (es decir, unilateral), entonces solo usamos una u otra.

En jamovi, si ejecutamos una ‘Prueba T de muestras independientes’ con puntuaciones como variable dependiente y grupo como la variable de agrupación, y luego en las opciones de ‘pruebas’ marcas la opción de $U$ Mann-Whitney, obtendremos resultados que muestran que $U = 3$ (es decir, el mismo número de marcas de verificación que se muestra arriba), y un valor p = $0.05556$. Ver Figure 11.26.

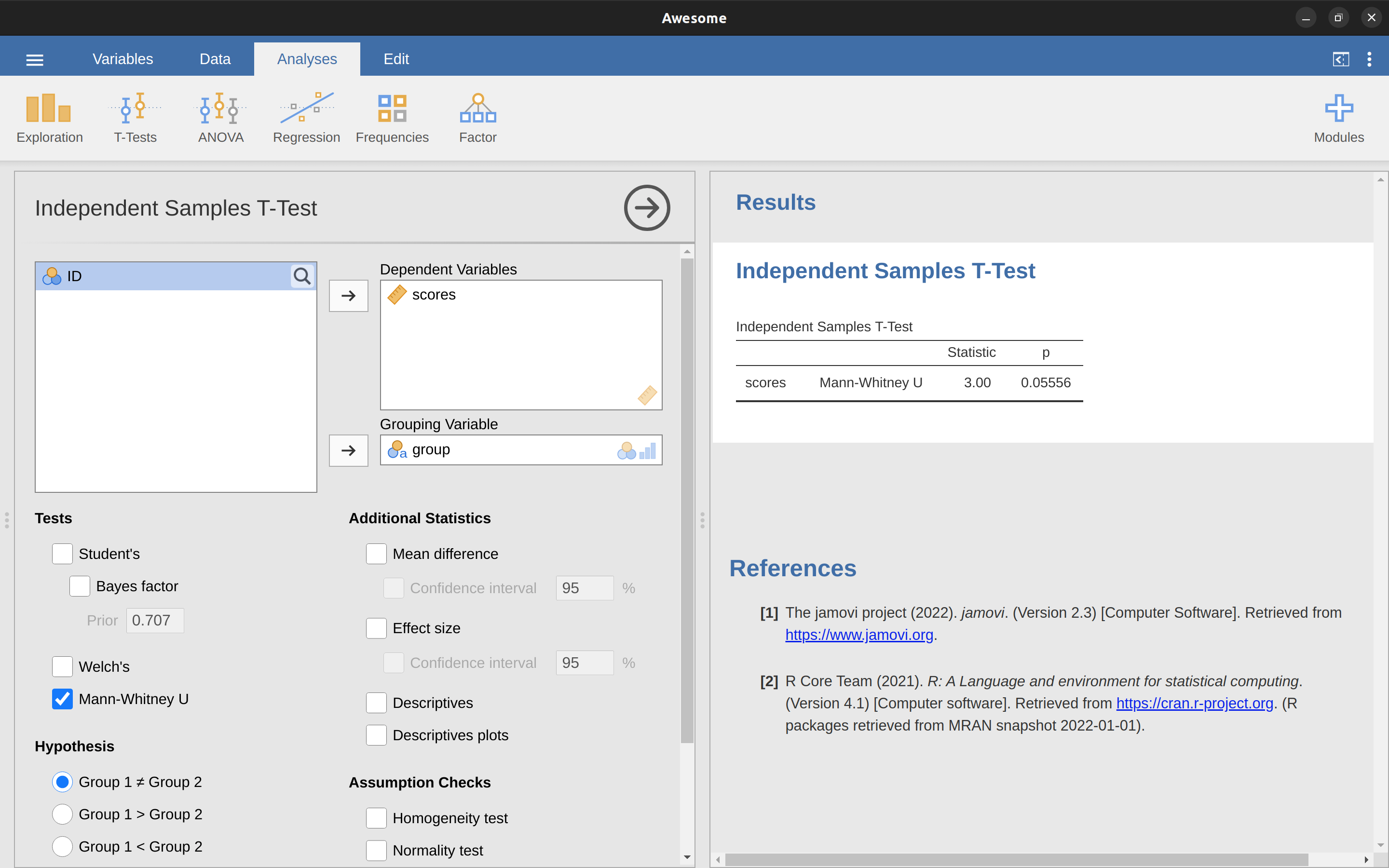
Figure 11.26: pantalla jamovi que muestra los resultados de la prueba $U$ Mann-Whitney

11.10.2 Prueba de Wilcoxon de una muestra

¿Qué pasa con la prueba de Wilcoxon de una muestra (o de manera equivalente, la prueba de Wilcoxon de muestras pareadas)? Supongamos que estoy interesada en saber si recibir una clase de estadística tiene algún efecto sobre la felicidad de los estudiantes. Mis datos están en el archivo luck.csv. Lo que he medido aquí es la felicidad de cada estudiante antes de recibir la clase y después de recibir la clase, y la puntuación de cambio es la diferencia entre los dos. Tal como vimos con la prueba t, no hay una diferencia fundamental entre hacer una prueba de muestras pareadas usando antes y después, versus hacer una prueba de una muestra usando las puntuaciones de cambio. Como antes, la forma más sencilla de pensar en la prueba es construir una tabulación. La forma de hacerlo esta vez es tomar esas puntuaciones de cambio que son diferencias positivas y tabularlas con respecto a toda la muestra completa. Lo que termina es una tabla que se parece a Table 11.5.

Table 11.5:
Comparación de observaciones por grupo para una prueba U de Wilcoxon de una muestra
		all differences
		$-24$	$-14$	$-10$	7	$-6$	$-38$	2	$-35$	$-30$	5
positive differences	7	.	.	.	$ \checkmark $	$ \checkmark $	.	$ \checkmark $	.	.	$ \checkmark $
	2	.	.	.	.	.	.	$ \checkmark $	.	.	.
	5	.	.	.	.	.	.	$ \checkmark $	.	.	$ \checkmark $

Contando las marcas de verificación esta vez obtenemos una una prueba estadística de $W = 7$. Como antes, si nuestra prueba es bilateral, rechazamos la hipótesis nula cuando W es muy grande o muy pequeña. En cuanto a ejecutarlo en jamovi, es más o menos lo que cabría esperar. Para la versión de una muestra, especifica la opción ‘Clasificación de Wilcoxon’ en ‘Pruebas’ en la ventana de análisis ‘Prueba T de una muestra’. Esto te da Wilcoxon $W = 7$, valor p = $0.03711$. Como esto demuestra, tenemos un efecto significativo. Evidentemente, tomar una clase de estadística tiene un efecto en tu felicidad. Cambiar a una versión de la prueba con muestras emparejadas no nos dará una respuesta diferente, por supuesto; ver Figure 11.27.

Figure 11.27: pantalla jamovi que muestra los resultados de las pruebas no paramétricas de Wilcoxon de una muestra y muestras emparejadas

11.11 Resumen

La prueba t de una muestra se utiliza para comparar la media de una sola muestra con un valor hipotético para la media poblacional.
Se utiliza una prueba t de muestras independientes para comparar las medias de dos grupos y prueba la hipótesis nula de que tienen la misma media. Viene en dos formas: La prueba t de muestras independientes (prueba de Student) (#sec-the-independent-samples-t-test-student-test) asume que los grupos tienen la misma desviación estándar, Las muestras independientes prueba t (prueba de Welch) no lo hace.
[La prueba t de muestras relacionadas] se usa cuando tienes dos puntuaciones de cada persona y deseas probar la hipótesis nula de que las dos puntuaciones tienen la misma media. Es equivalente a tomar la diferencia entre las dos puntuaciones para cada persona y luego ejecutar una prueba t de una muestra en las puntuaciones de diferencia.
[Las pruebas unilaterales] son perfectamente legítimas siempre que estén planificadas previamente (¡como todas las pruebas!).
Los cálculos de Tamaño del efecto para la diferencia entre las medias se pueden calcular a través del estadístico d de Cohen.
[Comprobación de la normalidad de una muestra] mediante gráficos QQ y la prueba de Shapiro-Wilk.
Si tus datos no son normales, puedes usar las pruebas de Mann-Whitney o Wilcoxon en lugar de las pruebas t para [Prueba de datos no normales].

La experimentación informal en mi jardín sugiere que sí. Los nativos australianos están adaptados a niveles bajos de fósforo en relación con cualquier otro lugar de la Tierra, por lo que si compraste una casa con un montón de plantas exóticas y quieres plantar nativas, manténlas separadas; los nutrientes para las plantas europeas son veneno para las australianas.↩︎
para hacer esto, tuve que cambiar el nivel de medida de $X$ a ‘Continuo’, ya que durante la apertura/importación del archivo csv jamovi lo convirtió en una variable de nivel nominal, que no es adecuada para mi análisis↩︎
adoptando la notación de Section 7.5, un estadístico podría escribir esto como: \[X \sum Normal(\mu_0,\sigma^2)\]↩︎
En otras palabras, si la hipótesis nula es verdadera, entonces la distribución muestral de la media se puede escribir de la siguiente manera: \[\bar{X} \sum Normal(\mu_0, ES(\bar{X})) \]↩︎
Nuevamente, puedes ver Section 4.5 si has olvidado por qué esto es cierto.↩︎
En realidad, esto es demasiado. Estrictamente hablando, la prueba z solo requiere que la distribución muestral de la media se distribuya normalmente. Si la población es normal, necesariamente se deduce que la distribución muestral de la media también es normal. Sin embargo, como vimos al hablar del teorema central del límite, es muy posible (incluso habitual) que la distribución muestral sea normal incluso si la distribución poblacional en sí misma no es normal. Sin embargo, a la luz de lo ridículo que resulta suponer que se conoce la verdadera desviación estándar, no tiene mucho sentido entrar en detalles al respecto.↩︎
Bueno, más o menos. Según entiendo la historia, Gosset solo proporcionó una solución parcial; Sir Ronald Fisher proporcionó la solución general al problema.↩︎
Más en serio, tiendo a pensar que lo contrario es cierto. Desconfío mucho de los informes técnicos que llenan sus secciones de resultados con nada más que números. Puede que sea sólo que soy una idiota arrogante, pero a menudo siento que un autor que no intenta explicar e interpretar su análisis al lector, o bien no lo entiende por sí mismo o bien es un poco perezoso. Tus lectores son inteligentes, pero no infinitamente pacientes. No les molestes si puedes evitarlo.↩︎
un comentario técnico. De la misma manera que podemos debilitar los supuestos de la prueba z para que solo estemos hablando de la distribución muestral, podemos debilitar los supuestos de la prueba t para que no tengamos que asumir la normalidad poblacional. Sin embargo, para la prueba t es más complicado hacer esto. Como antes, podemos reemplazar el supuesto de normalidad de la población con el supuesto de que la distribución muestral de $\bar{X}$ es normal. Sin embargo, recuerda que también confiamos en una estimación muestral de la desviación estándar, por lo que también requerimos que la distribución muestral de $\hat{\sigma}$ sea ji-cuadrado. Eso hace que las cosas sean más difíciles, y esta versión rara vez se usa en la práctica. Afortunadamente, si la distribución poblacional es normal, entonces se cumplen estos dos supuestos.↩︎
Aunque es el más simple, por eso empecé con él.↩︎
Casi siempre surge una pregunta divertida en este punto: ¿a qué diablos se refiere la población en este caso? ¿Es el grupo de estudiantes que realmente recibe la clase del Dr. Harpo (los 33)? ¿El conjunto de personas que podrían recibir la clase (un número desconocido de ellos)? ¿O algo mas? ¿Importa cuál de estos escojamos? Como mi alumnado me hace esta pregunta todos los años, daré una respuesta breve. Técnicamente sí, sí importa. Si cambias tu definición de lo que realmente es la población del “mundo real”, entonces la distribución muestral de tu media observada $\bar{X}$ también cambia. La prueba t se basa en el supuesto de que las observaciones se muestrean al azar de una población infinitamente grande y, en la medida en que la vida real no sea así, entonces la prueba t puede ser incorrecta. En la práctica, sin embargo, esto no suele ser un gran problema. Aunque el supuesto casi siempre es incorrecto, no conduce a una gran cantidad de comportamiento patológico de la prueba, por lo que tendemos a ignorarlo.↩︎
Matemáticamente, podemos escribir esto como \[w_1=N_1-1\] \[w_2=N_2-1\] Ahora que hemos asignado pesos a cada muestra calculamos la estimación combinada de la varianza cogiendo el promedio ponderado de las dos estimaciones de varianza, $\hat{sigma}_{1}^{2}$ y $\hat{sigma}_{2}^{2}$ \[ \hat{\sigma}_p^2=\frac{w_1\hat{\sigma}_1^2+w_2\hat{\sigma}_2^2}{w_1+w_2}\] Finalmente, convertimos la estimación de la varianza agrupada a una estimación de desviación estándar agrupada, haciendo la raíz cuadrada. \[\hat{\sigma}_p=\sqrt{\frac{w_1\hat{\sigma}_1^2+w_2\hat{\sigma}_2^2}{w_1+w_2}}\] Y si mentalmente sustituyes $(w_1 = N_1 - 1)$ y $w_2 = N_2 - 1$ en esta ecuación obtendrá una fórmula muy fea. Una fórmula muy fea que en realidad parece ser la forma “estándar” de describir la estimación de la desviación estándar agrupada. Sin embargo, no es mi forma favorita de pensar en las desviaciones estándar agrupadas. Prefiero pensarlo así. Nuestro conjunto de datos en realidad corresponde a un conjunto de N observaciones que se clasifican en dos grupos. Así que usemos la notación $X_{ik}$ para referirnos a la calificación recibida por el i-ésimo estudiante en el k-ésimo grupo de tutoría. Es decir, $(X_{11}$ es la calificación que recibió el primer estudiante en la clase de Anastasia, $X_{21}$ es su segundo estudiante, y así sucesivamente. Y tenemos dos medias grupales separadas $\bar{X} _1$ y $\bar{X}_2$, a las que podríamos referirnos “genéricamente” usando la notación $\bar{X}_k$, es decir, la calificación media para el k-ésimo grupo de tutoría. Hasta ahora, todo bien. Ahora, dado que cada estudiante cae en una de las dos tutorías, podemos describir su desviación de la media del grupo como la diferencia \[X_{ik}-\bar{X}_k\] Entonces, ¿por qué no usar estas desviaciones (es decir, ¿en qué medida la calificación de cada estudiante difiere de la calificación media en su tutoría?). Recuerda, una varianza es solo el promedio de un montón de desviaciones al cuadrado, así que hagamos eso. Matemáticamente, podríamos escribirlo así \[\ frac{\sum_{ik}(X_{ik}-\bar{X}_k)^2}{N}\] donde la notación “$\sum_{ik}$” es una forma perezosa de decir “calcular una suma mirando a todos los estudiantes en todas las tutorías”, ya que cada “$_{ik}$” corresponde a un estudiante.$^a$ Pero, como vimos en Section 8.5, calcular la varianza dividiendo por N produce una estimación sesgada de la varianza de la población. Y previamente necesitábamos dividir por $(N - 1)$ para arreglar esto. Sin embargo, como mencioné en ese momento, la razón por la que existe este sesgo es que la estimación de la varianza se basa en la media muestral y, en la medida en que la media muestral no es igual a la media poblacional, puede sesgar sistemáticamente nuestra estimación de la media. ¡Pero esta vez nos basamos en dos medias muestrales! ¿Significa esto que tenemos más sesgos? Sí, eso significa. ¿Significa esto que ahora debemos dividir por $(N - 2)$ en lugar de $(N - 1)$, para calcular nuestra estimación de la varianza agrupada? Pues sí \[\hat {\sigma}_p^2=\frac{\sum_{ik}(X_{ik}-\bar{X}_k)^2}{N-2}\] Ah, y si sacas la raíz cuadrada de esto entonces obtienes $\hat{\sigma}_p$, la estimación de la desviación estándar agrupada. En otras palabras, el cálculo de la desviación estándar agrupada no es nada especial. No es muy diferente al cálculo de la desviación estándar normal.
—
$^a$ Se introducirá una notación más correcta en Chapter 13.↩︎
Siempre que las dos variables realmente tengan la misma desviación estándar, nuestra estimación del error estándar es \[SE(\bar{X}_1-\bar{X }_2)=\hat{\sigma}\sqrt{\frac{1}{N_1}+\frac{1}{N_2}}\] y nuestro estadístico t es por lo tanto \[t=\frac{\bar{ X}_1-\bar{X}_2}{SE(\bar{X}_1-\bar{X}_2)}\]↩︎
Estrictamente hablando, es la diferencia en las medias lo que debería distribuirse normalmente, pero si ambos grupos tienen datos normalmente distribuidos, entonces la diferencia en las medias también estará normalmente repartida. En la práctica, el teorema central del límite nos asegura que, en general, las distribuciones de las medias de las dos muestras que se prueban se aproximarán a las distribuciones normales a medida que los tamaños de las muestras aumentan, independientemente de las distribuciones de los datos subyacentes.↩︎
Bueno, supongo que puedes promediar manzanas y naranjas, y lo que obtienes al final es un delicioso batido de frutas. Pero nadie piensa realmente que un batido de frutas sea una buena manera de describir las frutas originales, ¿verdad?↩︎
pero aún se puede estimar el error estándar de la diferencia entre las medias muestrales, sólo que tiene un aspecto diferente \[SE(\bar{X}_1-\bar{X} _2)=\sqrt{\frac{\hat{\sigma}_1^2}{N_1}+\frac{\hat{\sigma}_2^2}{N_2}}\] La razón por la que se calcula de esta manera va más allá del alcance de este libro. Lo que importa para nuestros propósitos es que el estadístico t que surge de la prueba t de Welch es en realidad algo diferente al que surge de la prueba t de Student.↩︎
este diseño es muy similar al que motivó la prueba de McNemar (Section 10.7). Esto no debería ser una sorpresa. Ambos son diseños estándar de medidas repetidas que involucran dos medidas. La única diferencia es que esta vez nuestra variable de resultado está en una escala de intervalo (capacidad de la memoria de trabajo) en lugar de una variable de escala nominal binaria (una pregunta de sí o no).↩︎
En este punto tenemos a los Drs. Harpo, Chico y Zeppo. No hay premios por adivinar quién es el Dr. Groucho.↩︎
Introducen una pequeña corrección al multiplicar el valor habitual de $d$ por $\frac{(N - 3)}{(N - 2.25)}$.↩︎
si estás interesada, puedes ver cómo se hizo esto en el archivo chico2.omv↩︎
esta es una simplificación excesiva.↩︎
O eso, o la prueba de Kolmogorov-Smirnov, que probablemente sea más tradicional que la de Shapiro-Wilk. Aunque la mayoría de las cosas que he leído parecen sugerir que Shapiro-Wilk es la mejor prueba de normalidad, Kolomogorov Smirnov es una prueba de propósito general de equivalencia distribucional que se puede adaptar para manejar otros tipos de pruebas de distribución. En jamovi se prefiere la prueba de Shapiro-Wilk.↩︎
la prueba estadística que calcula se denota convencionalmente como $W$ y se calcula de la siguiente manera. Primero, clasificamos las observaciones en orden creciente y dejamos que $\bar{X_1}$ sea el valor más pequeño de la muestra, $X_2$ el segundo más pequeño y así sucesivamente. Entonces el valor de $W$ viene dado por \[W=\frac{(\sum_{i=1}^N a_iX_i)^2}{\sum_{i=1}^N(X_i-\bar{X} )^2}\] donde $\bar{X}$ es la media de las observaciones, y los valores de $a_i$ son … algo complicado que está fuera del alcance de un texto introductorio.↩︎
en realidad, hay dos versiones diferentes de la prueba estadística que difieren entre sí por un valor constante. La versión que he descrito es la que calcula jamovi.↩︎

		all differences
		\(-24\)	\(-14\)	\(-10\)	7	\(-6\)	\(-38\)	2	\(-35\)	\(-30\)	5
positive differences	7	.	.	.	\( \checkmark \)	\( \checkmark \)	.	\( \checkmark \)	.	.	\( \checkmark \)
	2	.	.	.	.	.	.	\( \checkmark \)	.	.	.
	5	.	.	.	.	.	.	\( \checkmark \)	.	.	\( \checkmark \)