| variable | min | max | mean | median | std. dev | IQR |
|---|---|---|---|---|---|---|
| Dani's grumpiness | 41 | 91 | 63.71 | 62 | 10.05 | 14 |
| Dani's hours slept | 4.84 | 9.00 | 6.97 | 7.03 | 1.02 | 1.45 |
| Dani's son's hours slept | 3.25 | 12.07 | 8.05 | 7.95 | 2.07 | 3.21 |
12 Correlación y regresión lineal
El objetivo de este capítulo es presentar la correlación y la regresión lineal. Estas son las herramientas estándar en las que confían los estadísticos para analizar la relación entre factores predictores continuos y resultados continuos.
12.1 Correlaciones
En esta sección hablaremos sobre cómo describir las relaciones entre variables en los datos. Para ello, hablaremos principalmente de la correlación entre variables. Pero primero, necesitamos algunos datos (Table 12.1).
12.1.1 Los datos
Pasemos a un tema cercano al corazón de todos los padres: el sueño. El conjunto de datos que usaremos es ficticio, pero está basado en hechos reales. Supongamos que tengo curiosidad por saber cuánto afectan los hábitos de sueño de mi hijo pequeño a mi estado de ánimo. Digamos que puedo calificar mi mal humor con mucha precisión, en una escala de 0 (nada malhumorado) a \(100\) (malhumorado como un anciano o una anciana muy, muy gruñona). Y supongamos también que he estado midiendo mi mal humor, mis patrones de sueño y los patrones de sueño de mi hijo desde hace bastante tiempo. Digamos, durante \(100\) días. Y, siendo un nerd, guardé los datos en un archivo llamado parenthood.csv. Si cargamos los datos podemos ver que el archivo contiene cuatro variables dani.sleep, baby.sleep, dani.grump y day. Ten en cuenta que cuando cargues este conjunto de datos por primera vez, es posible que jamovi no haya adivinado correctamente el tipo de datos para cada variable, en cuyo caso debes corregirlo: dani.sleep, baby.sleep, dani.grump y day pueden especificarse como variables continuas, e ID es una variable nominal (entera).1
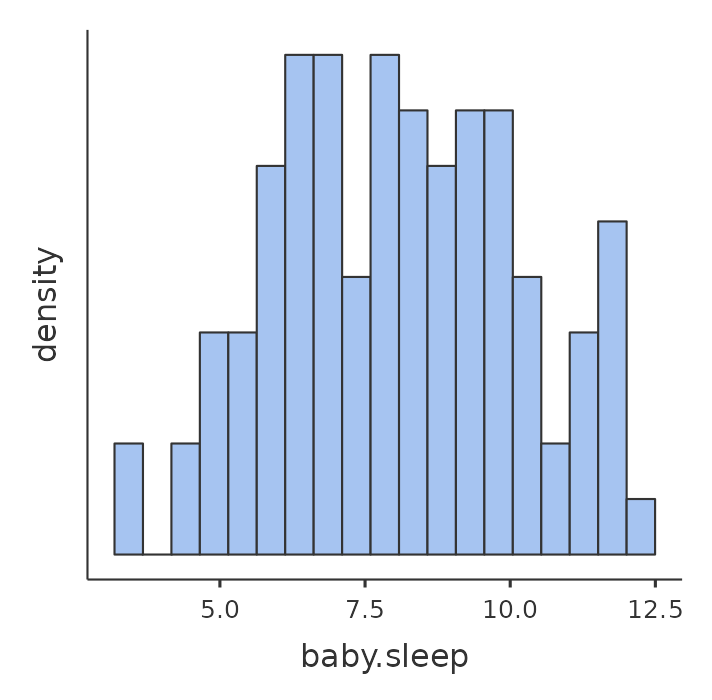
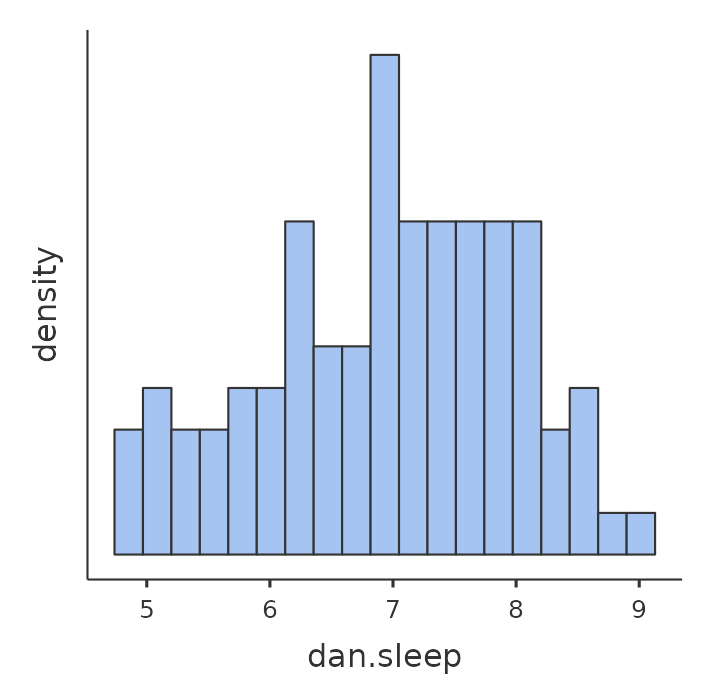
A continuación, echaré un vistazo a algunos estadísticos descriptivos básicos y, para dar una descripción gráfica de cómo son cada una de las tres variables interesantes, Figure 12.1 presenta histogramas. Una cosa a tener en cuenta: el hecho de que jamovi pueda calcular docenas de estadísticos diferentes no significa que debas informarlos todos. Si estuviera escribiendo esto para un informe, probablemente elegiría los estadísticos que son de mayor interés para mí (y para mis lectores) y luego los colocaría en una tabla agradable y simple como la de la Tabla 12.1.2 Ten en cuenta que cuando lo puse en una tabla, le di a todo nombres “legibles por humanos”. Esta es siempre una buena práctica. Nota también que no estoy durmiendo lo suficiente. Esta no es una buena práctica, pero otros padres me dicen que es bastante estándar.

12.1.2 La fuerza y la dirección de una relación
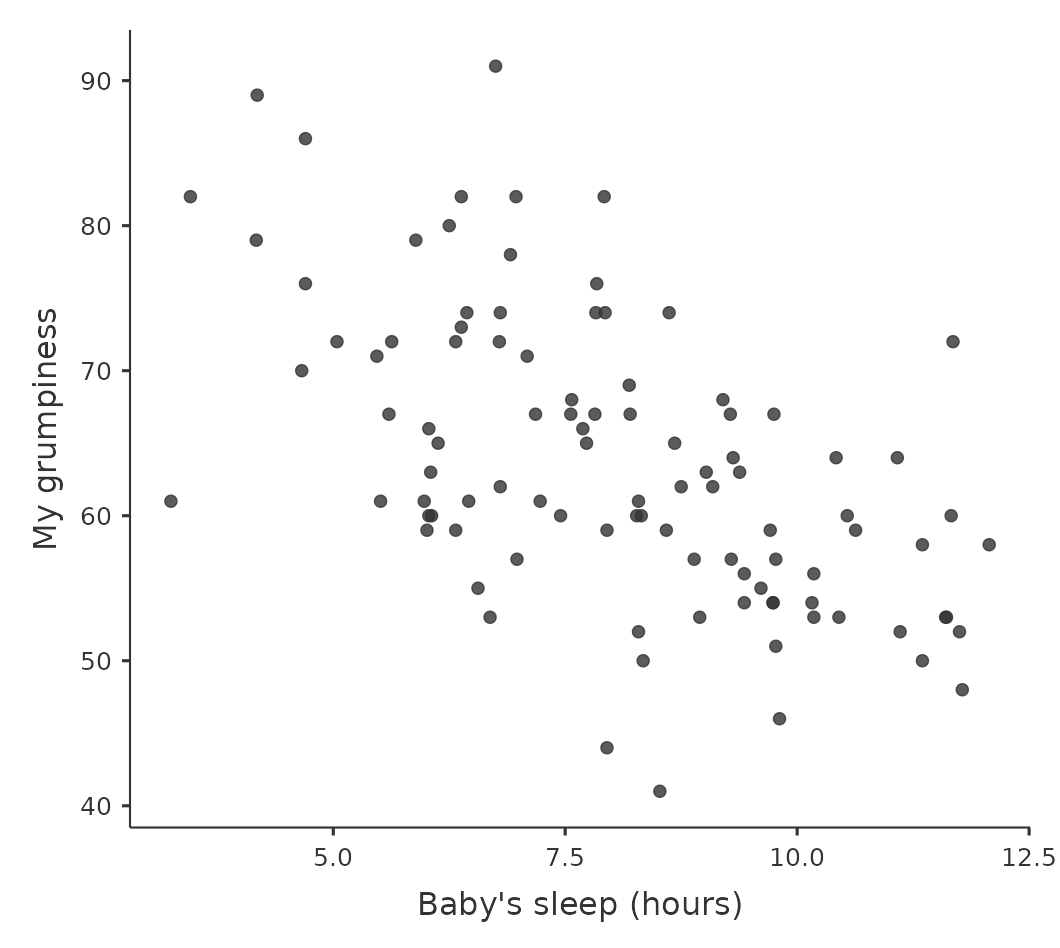
Podemos dibujar diagramas de dispersión para tener una idea general de cuán estrechamente relacionadas están dos variables. Sin embargo, idealmente, podríamos querer decir un poco más al respecto. Por ejemplo, comparemos la relación entre baby.sleep y dani.grump (Figure 12.1 (a)), izquierda, con la de dani.sleep y dani.grump (Figure 12.1 (b)), derecha. Al mirar estos dos gráficos uno al lado del otro, está claro que la relación es cualitativamente la misma en ambos casos: ¡más sueño equivale a menos mal humor! Sin embargo, también es bastante obvio que la relación entre dani.sleep y dani.grump es más fuerte que la relación entre baby.sleep y dani.grump. El gráfico de la derecha es “más ordenado” que el de la izquierda. Lo que parece es que si quieres predecir cuál es mi estado de ánimo, te ayudaría un poco saber cuántas horas durmió mi hijo, pero sería más útil saber cuántas horas dormí yo.

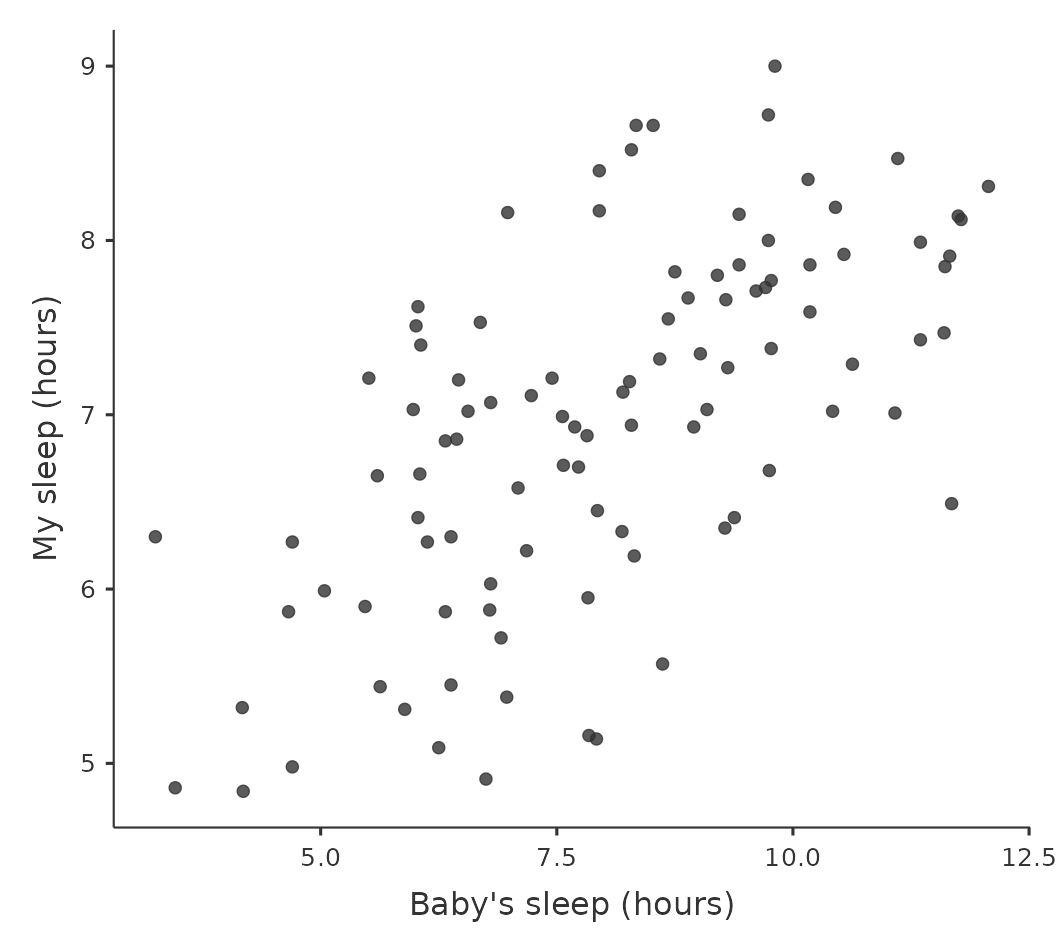
Por el contrario, consideremos los dos diagramas de dispersión que se muestran en Figure 12.3. Si comparamos el diagrama de dispersión de “baby.sleep v dani.grump” (izquierda) con el diagrama de dispersión de “’baby.sleep v dani.sleep” (derecha), la fuerza general de la relación es la misma, pero la dirección es diferente. Es decir, si mi hijo duerme más, yo duermo más (relación positiva, lado derecho), pero si él duerme más, yo me pongo menos gruñón (relación negativa, lado izquierdo).

12.1.3 El coeficiente de correlación
Podemos hacer estas ideas un poco más explícitas introduciendo la idea de un coeficiente de correlación (o, más específicamente, el coeficiente de correlación de Pearson), que tradicionalmente se denota como r. El coeficiente de correlación entre dos variables \(X\) y \(Y\) (a veces denominado \(r_{XY}\) ), que definiremos con más precisión en la siguiente sección, es una medida que varía de -1 a 1. Cuando \(r = -1\) significa que tenemos una relación negativa perfecta, y cuando \(r = 1\) significa que tenemos una relación positiva perfecta. Cuando \(r = 0\), no hay ninguna relación. Si observas Figure 12.4, puedes ver varios gráficos que muestran cómo son las diferentes correlaciones.
[Detalle técnico adicional 3]
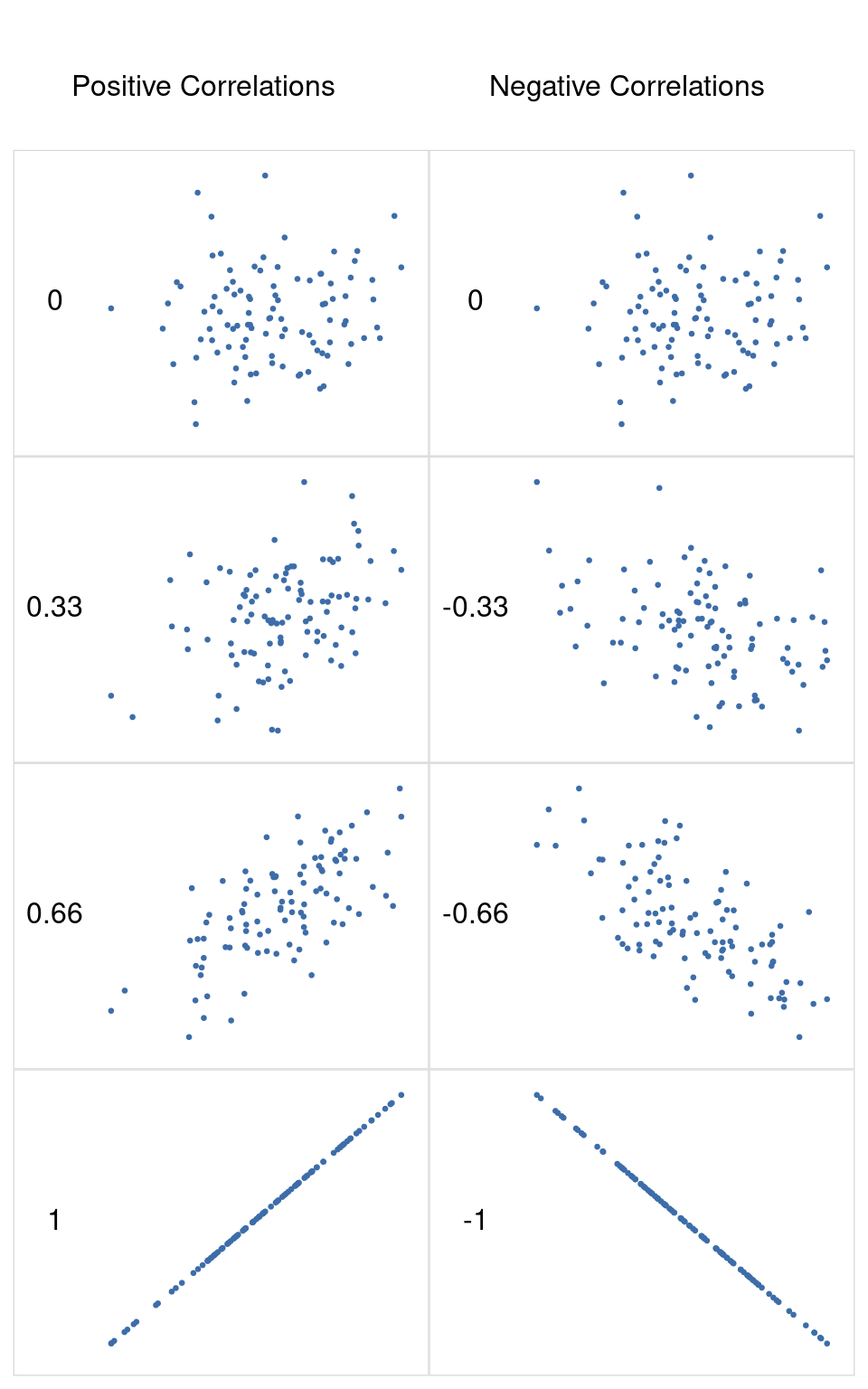
Al estandarizar la covarianza, no solo mantenemos todas las buenas propiedades de la covarianza discutidas anteriormente, sino que los valores reales de r están en una escala significativa: r = 1 implica una relación positiva perfecta y \(r = -1\) implica una relación negativa perfecta. Me extenderé un poco más sobre este punto más adelante, en la sección sobre [Interpretación de una correlación]. Pero antes de hacerlo, veamos cómo calcular correlaciones en jamovi.
12.1.4 Cálculo de correlaciones en jamovi
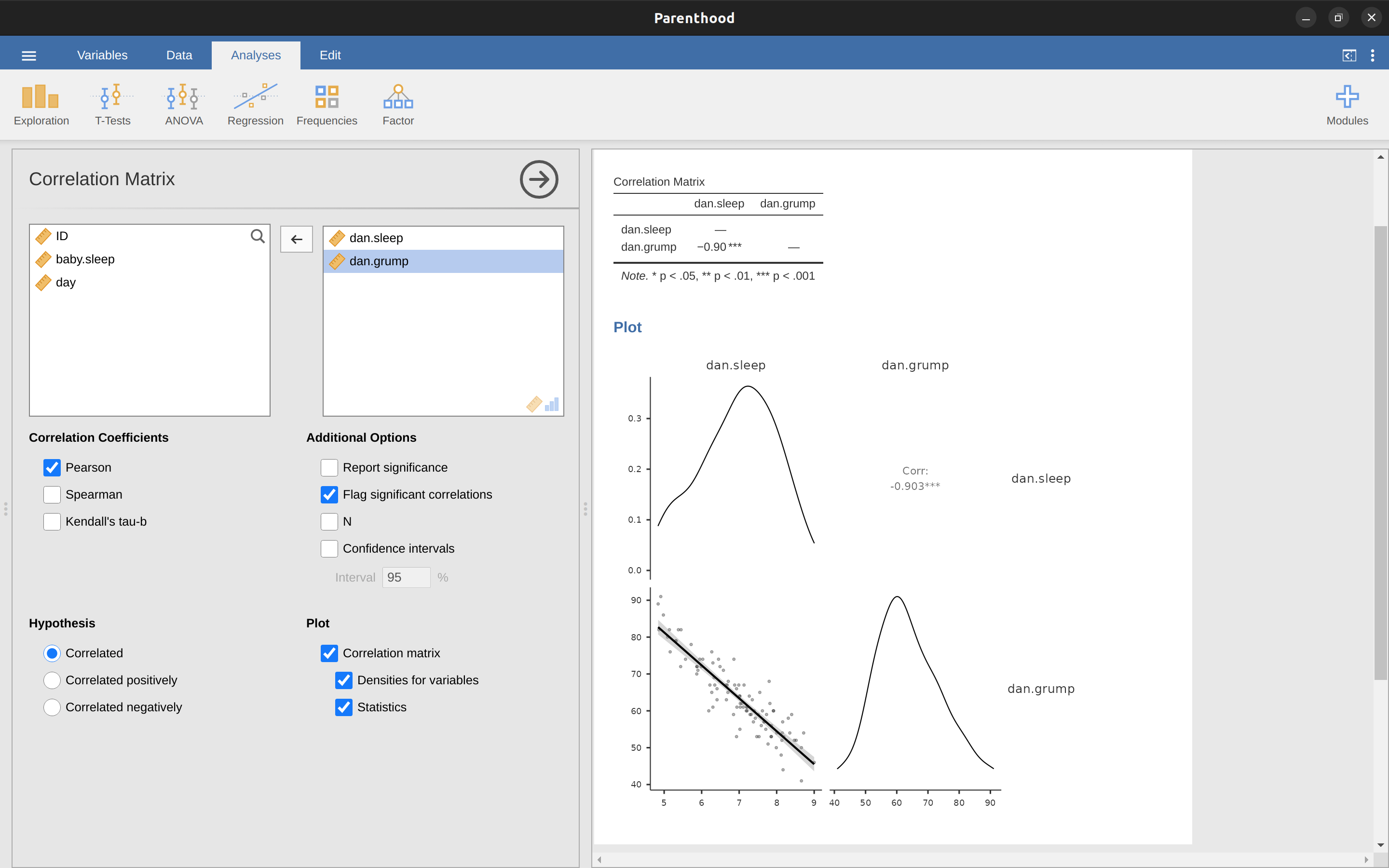
El cálculo de correlaciones en jamovi se puede hacer haciendo clic en el botón ‘Regresión’ - ‘Matriz de correlación’. Transfiere las cuatro variables continuas al cuadro de la derecha para obtener el resultado en Figure 12.5.

12.1.5 Interpretar una correlación
Naturalmente, en la vida real no se ven muchas correlaciones de \(1\). Entonces, ¿cómo deberías interpretar una correlación de, digamos, r = \(.4\)? La verdad es que realmente depende de para qué deseas usar los datos y de cómo de fuertes tienden a ser las correlaciones en tu campo. Un amigo mío en ingeniería argumentó una vez que cualquier correlación menor a \(.95\) es completamente inútil (creo que estaba exagerando, incluso para la ingeniería). Por otro lado, hay casos reales, incluso en psicología, en los que realmente deberías esperar correlaciones tan fuertes. Por ejemplo, uno de los conjuntos de datos de referencia utilizados para probar las teorías de cómo las personas juzgan las similitudes es tan limpio que cualquier teoría que no pueda lograr una correlación de al menos \(.9\) realmente no se considera exitosa. Sin embargo, al buscar (digamos) correlatos elementales de inteligencia (por ejemplo, tiempo de inspección, tiempo de respuesta), si obtienes una correlación superior a \(.3\), lo estás haciendo muy bien. En resumen, la interpretación de una correlación depende mucho del contexto. Dicho esto, la guía aproximada que se presenta en Table 12.2 es bastante típica.
| Correlation | Strength | Direction |
|---|---|---|
| -1.00 to -0.90 | Very strong | Negative |
| -0.90 to -0.70 | Strong | Negative |
| -0.70 to -0.40 | Moderate | Negative |
| -0.40 to -0.20 | Weak | Negative |
| -0.20 to 0.00 | Negligible | Negative |
| 0.00 to 0.20 | Negligible | Positive |
| 0.20 to 0.40 | Weak | Positive |
| 0.40 to 0.70 | Moderate | Positive |
| 0.70 to 0.90 | Strong | Positive |
| 0.90 to 1.00 | Very strong | Positive |
| *Note that I say a rough guide. There aren't hard and fast rules for what counts as strong or weak relationships. It depends on the context | ||
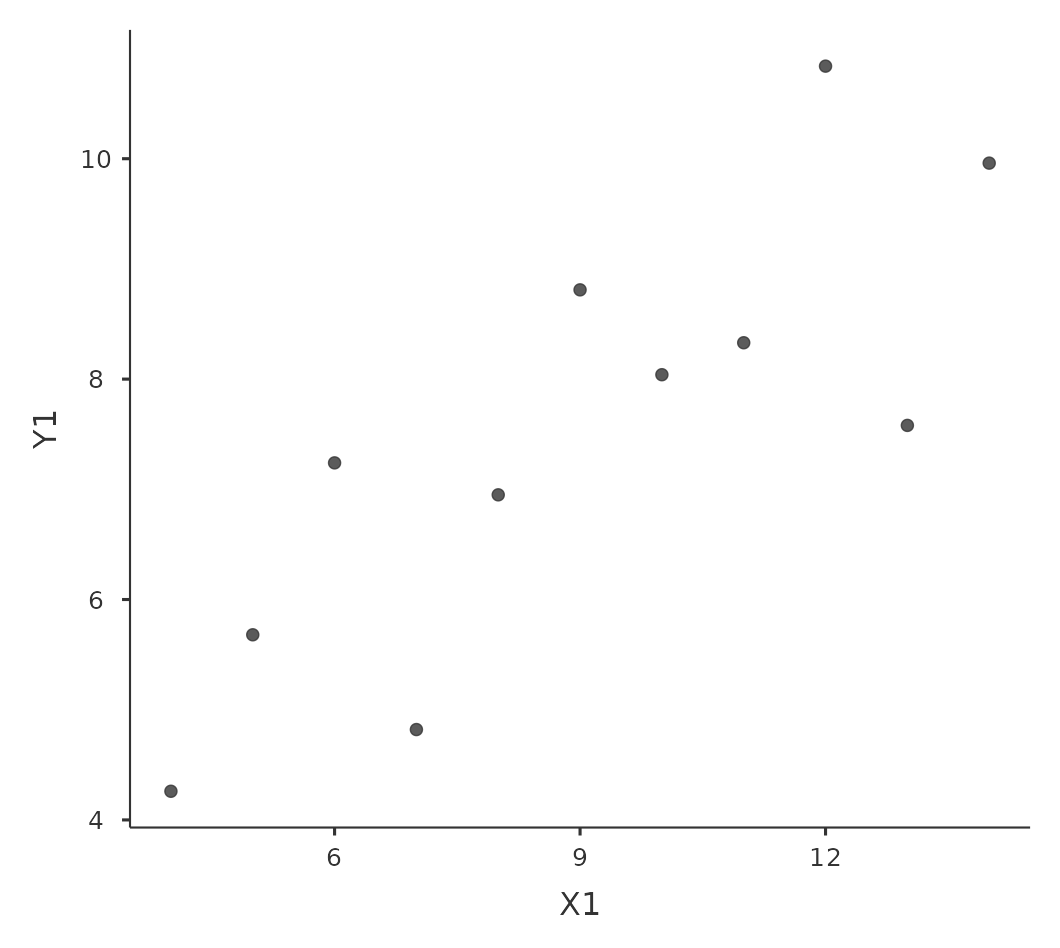
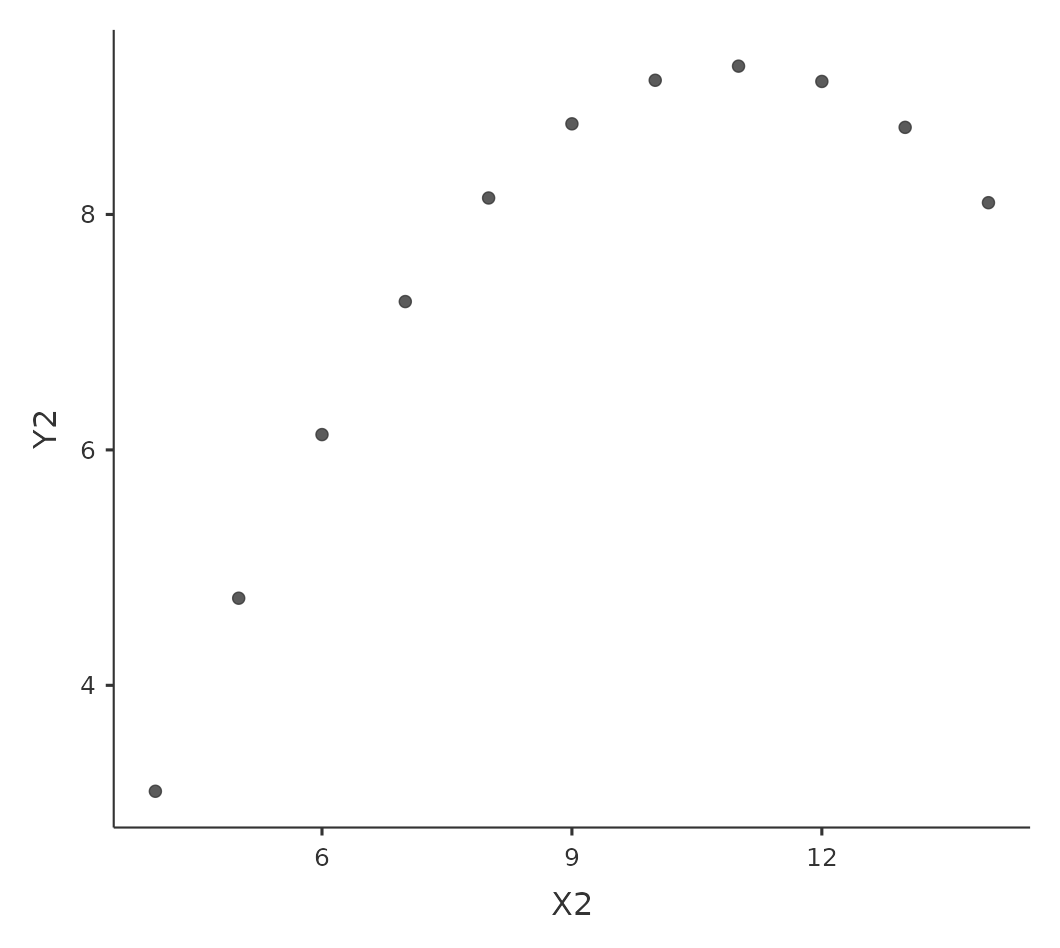
Sin embargo, algo que nunca se puede enfatizar lo suficiente es que siempre debes mirar el diagrama de dispersión antes de adjuntar cualquier interpretación a los datos. Una correlación podría no significar lo que crees que significa. La ilustración clásica de esto es el “Cuarteto de Anscombe” (Anscombe, 1973), una colección de cuatro conjuntos de datos. Cada conjunto de datos tiene dos variables, \(X\) y \(Y\). Para los cuatro conjuntos de datos, el valor medio para \(X\) es \(9\) y el valor medio para \(Y\) es \(7,5\). Las desviaciones estándar de todas las variables \(X\) son casi idénticas, al igual que las de las variables Y. Y en cada caso la correlación entre \(X\) y \(Y\) es \(r = 0.816\). Puedes verificar esto tú misma, ya que lo guardé en un archivo llamado anscombe.csv.
Una pensaría que estos cuatro conjuntos de datos serían bastante similares entre sí. Pero no lo son. Si dibujamos diagramas de dispersión de \(X\) contra \(Y\) para las cuatro variables, como se muestra en Figure 12.6, vemos que los cuatro son espectacularmente diferentes entre sí. La lección aquí, que mucha gente parece olvidar en la vida real, es “siempre representar gráficamente tus datos sin procesar” (ver Chapter 5).


12.1.6 Correlaciones de rango de Spearman
El coeficiente de correlación de Pearson es útil para muchas cosas, pero tiene deficiencias. Destaca una cuestión en particular: lo que realmente mide es la fuerza de la relación lineal entre dos variables. En otras palabras, lo que le da es una medida de la medida en que todos los datos tienden a caer en una sola línea perfectamente recta. A menudo, esta es una aproximación bastante buena a lo que queremos decir cuando decimos “relación”, por lo que es bueno calcular la correlación de Pearson. A veces, sin embargo, no lo es.
Una situación muy común en la que la correlación de Pearson no es lo correcto surge cuando un aumento en una variable \(X\) realmente se refleja en un aumento en otra variable Y , pero la naturaleza de la relación no es necesariamente lineal. Un ejemplo de esto podría ser la relación entre el esfuerzo y la recompensa al estudiar para un examen. Si no te esfuerzas (\(X\)) en aprender una materia, deberías esperar una calificación de \(0\%\) (\(Y\)). Sin embargo, un poco de esfuerzo causará una mejora masiva. El solo hecho de asistir a las clases significa que aprendes bastante, y si solo llegas a las clases y garabateas algunas cosas, tu calificación podría subir al 35%, todo sin mucho esfuerzo. Sin embargo, no obtienes el mismo efecto en el otro extremo de la escala. Como todo el mundo sabe, se necesita mucho más esfuerzo para obtener una calificación de \(90\%\) que para obtener una calificación de \(55\%\). Lo que esto significa es que, si tengo datos que analizan el esfuerzo de estudio y las calificaciones, hay muchas posibilidades de que las correlaciones de Pearson sean engañosas.
Para ilustrar, considera los datos representados en Figure 12.7, que muestran la relación entre las horas trabajadas y la calificación recibida por 10 estudiantes que reciben alguna clase. Lo curioso de este conjunto de datos (muy ficticios) es que aumentar tu esfuerzo siempre aumenta tu nota. Puede ser por mucho o por poco, pero aumentar el esfuerzo nunca disminuirá tu calificación. Si ejecutamos una correlación estándar de Pearson, muestra una fuerte relación entre las horas trabajadas y la calificación recibida, con un coeficiente de correlación de \(0.91\). Sin embargo, esto en realidad no refleja el hecho de que aumentar las horas trabajadas siempre aumenta la calificación. Aquí queremos poder decir que la correlación es perfecta pero para una noción algo diferente de lo que es una “relación”. Lo que estamos buscando es algo que capte el hecho de que aquí hay una relación ordinal perfecta. Es decir, si el estudiante 1 trabaja más horas que el estudiante 2, entonces podemos garantizar que el estudiante 1 obtendrá la mejor calificación. Eso no es lo que dice una correlación de \(r = .91\).
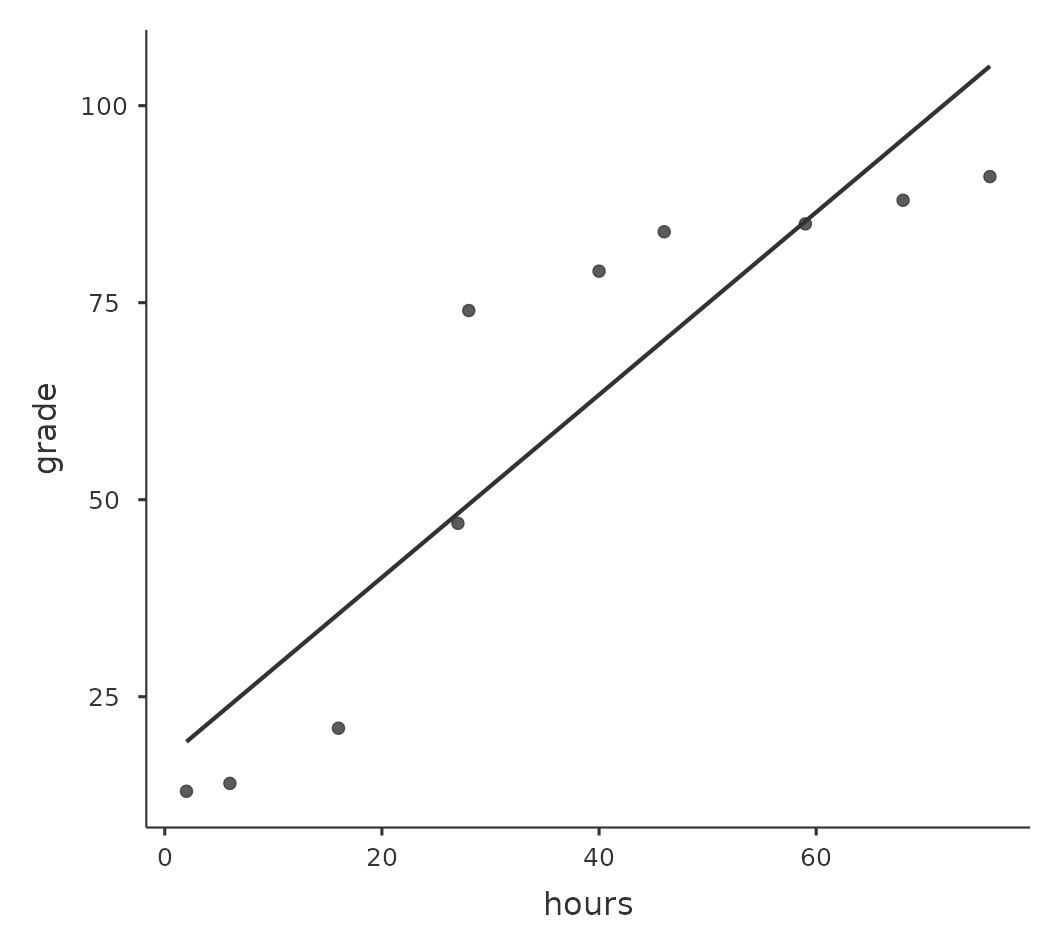
¿Cómo debemos abordar esto? En realidad, es muy fácil. Si estamos buscando relaciones ordinales, todo lo que tenemos que hacer es tratar los datos como si fueran una escala ordinal. Así, en lugar de medir el esfuerzo en términos de “horas trabajadas”, clasifiquemos nuestros \(10\) estudiantes en orden de horas trabajadas. Es decir, el estudiante \(1\) hizo la menor cantidad de trabajo de todos (\(2\) horas), por lo que obtuvo el rango más bajo (rango = \(1\)). El estudiante \(4\) fue el siguiente más perezoso, dedicando solo \(6\) horas de trabajo durante todo el semestre, por lo que obtiene el siguiente rango más bajo (rango = \(2\)). Ten en cuenta que estoy usando “rango = 1” para hacer referencia a “rango bajo”. A veces, en el lenguaje cotidiano, hablamos de “rango = $ 1 $” para hacer referencia a “rango superior” en lugar de “rango inferior”. Así que ten cuidado, puedes clasificar “del valor más pequeño al valor más grande” (es decir, pequeño equivale a rango \(1\)) o puedes clasificar “del valor más grande al valor más pequeño” (es decir, grande equivale a rango 1). En este caso, estoy clasificando de menor a mayor, pero como es muy fácil olvidar de qué manera configuraste las cosas, ¡tienes que esforzarte un poco para recordar!
Bien, echemos un vistazo a nuestros estudiantes cuando los clasificamos de peor a mejor en términos de esfuerzo y recompensa Table 12.3.
| rank (hours worked) | rank (grade received) | |
|---|---|---|
| student 1 | 1 | 1 |
| student 2 | 10 | 10 |
| student 3 | 6 | 6 |
| student 4 | 2 | 2 |
| student 5 | 3 | 3 |
| student 6 | 5 | 5 |
| student 7 | 4 | 4 |
| student 8 | 8 | 8 |
| student 9 | 7 | 7 |
| student 10 | 9 | 9 |
Mmm. Estos son idénticos. El estudiante que se esforzó más obtuvo la mejor calificación, el estudiante que se esforzó menos obtuvo la peor calificación, etc. Como muestra la tabla anterior, estas dos clasificaciones son idénticas, por lo que si ahora las correlacionamos obtenemos una relación perfecta, con una correlación de 1.0.
Lo que acabamos de reinventar es la correlación de orden de rango de Spearman, generalmente denominada \(\rho\) para distinguirla de la correlación r de Pearson. Podemos calcular el \(\rho\) de Spearman usando jamovi simplemente haciendo clic en la casilla de verificación ‘Spearman’ en la pantalla ‘Correlation Matrix’.
12.2 Gráfico de dispersión
Los diagramas de dispersión son una herramienta simple pero efectiva para visualizar la relación entre dos variables, como vimos con las figuras en la sección sobre Correlaciones. Es esta última aplicación la que generalmente tenemos en mente cuando usamos el término “diagrama de dispersión”. En este tipo de gráfico, cada observación corresponde a un punto. La ubicación horizontal del punto traza el valor de la observación en una variable y la ubicación vertical muestra su valor en la otra variable. En muchas situaciones, realmente no tienes una opinión clara sobre cuál es la relación causal (por ejemplo, A causa B, o B causa A, o alguna otra variable C controla tanto A como B). Si ese es el caso, realmente no importa qué variable representas gráficamente en el eje x y cuál representas en el eje y. Sin embargo, en muchas situaciones tienes una idea bastante clara de qué variable crees que es más probable que sea causal, o al menos tienes algunas sospechas que van en esa dirección. Si es así, entonces es usual representar la variable de causa en el eje x y la variable de efecto en el eje y. Con eso en mente, veamos cómo dibujar diagramas de dispersión en jamovi, usando el mismo conjunto de datos de paternidad (es decir, parenthood.csv) que usé cuando introduje las correlaciones.
Supongamos que mi objetivo es dibujar un diagrama de dispersión que muestre la relación entre la cantidad de sueño que duermo (dani.sleep) y lo malhumorada que estoy al día siguiente (dani.grump). Podemos obtener el gráfico que buscamos de dos maneras diferentes en jamovi. La primera forma es usar la opción ‘Gráfica’ debajo del botón ‘Regresión’ - ‘Matriz de correlación’, dándonos el resultado que se muestra en Figure 12.8. Ten en cuenta que jamovi dibuja una línea a través de los puntos, hablaremos de esto un poco más adelante en la sección sobre ¿Qué es un modelo de regresión lineal?. Trazar un diagrama de dispersión de esta manera también te permite especificar ‘Densidades para variables’ y esta opción agrega una curva de densidad que muestra cómo se distribuyen los datos en cada variable.
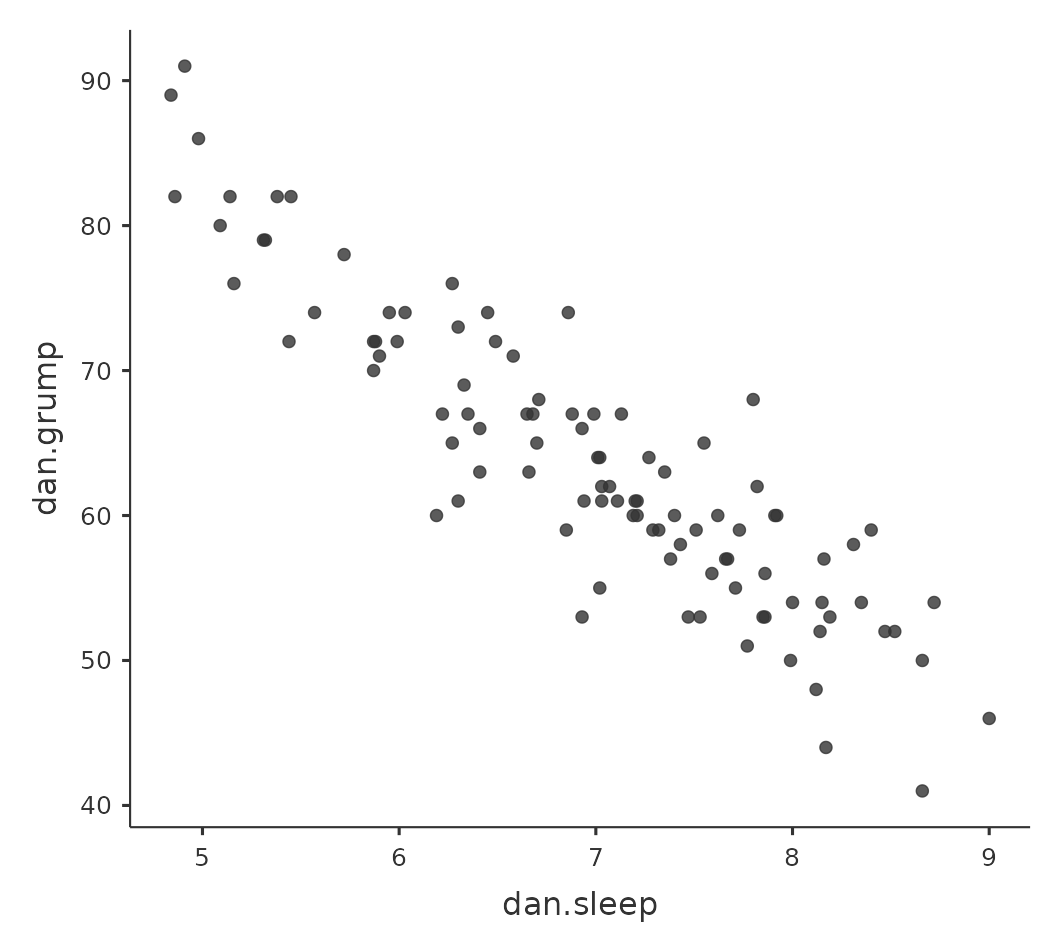
La segunda forma de hacerlo es usar uno de los módulos complementarios de jamovi. Este módulo se llama ‘scatr’ y puedes instalarlo haciendo clic en el icono grande ‘\(+\)’ en la parte superior derecha de la pantalla de jamovi, abriendo la librería de jamovi, desplazándote hacia abajo hasta encontrar ‘scatr’ y haciendo clic en ‘instalar’. Cuando hayas hecho esto, encontrarás un nuevo comando ‘Gráfico de dispersión’ disponible en el botón ‘Exploración’. Este gráfico es un poco diferente al primero, ver Figure 12.9, pero la información relevante es la misma.
12.2.1 Opciones más elaboradas
A menudo querrás ver las relaciones entre varias variables a la vez, usando una matriz de diagrama de dispersión (en jamovi a través del comando ‘Matriz de correlación’ - ‘Gráfica’). Simplemente agrega otra variable, por ejemplo, baby.sleep a la lista de variables a correlacionar, y jamovi creará una matriz de diagrama de dispersión para ti, como la de Figure 12.10.

12.3 ¿Qué es un modelo de regresión lineal?
Reducidos a lo esencial, los modelos de regresión lineal son básicamente una versión un poco más elegante de la correlación de Pearson (consulta Correlaciones), aunque, como veremos, los modelos de regresión son herramientas mucho más poderosas.
Dado que las ideas básicas de la regresión están estrechamente relacionadas con la correlación, volveremos al archivo parenthood.csv que estábamos usando para ilustrar cómo funcionan las correlaciones. Recuerda que, en este conjunto de datos, estábamos tratando de averiguar por qué Dani está tan malhumorada todo el tiempo y nuestra hipótesis de trabajo era que no estoy durmiendo lo suficiente. Dibujamos algunos diagramas de dispersión para ayudarnos a examinar la relación entre la cantidad de sueño que duermo y mi mal humor al día siguiente, como en Figure 12.9, y como vimos anteriormente, esto corresponde a una correlación de $r = -.90 $, pero nos encontramos imaginando en secreto algo que se parece más a Figure 12.11 (a). Es decir, dibujamos mentalmente una línea recta a través de la mitad de los datos. En estadística, esta línea que estamos dibujando se llama línea de regresión. Ten en cuenta que la línea de regresión pasa por la mitad de los datos. No nos imaginamos nada parecido al gráfico que se muestra en Figure 12.11 (b).

Esto no es muy sorprendente. La línea que he dibujado en Figure 12.11 (b) no “encaja” muy bien con los datos, por lo que no tiene mucho sentido proponerla como una forma de resumir los datos, ¿verdad? Esta es una observación muy simple, pero resulta ser muy poderosa cuando empezamos a tratar de envolverla con un poco de matemática. Para hacerlo, comencemos con un repaso de algunas matemáticas de la escuela secundaria. La fórmula de una línea recta generalmente se escribe así
\[y=a+bx\]
O, al menos, así era cuando fui a la escuela secundaria hace tantos años. Las dos variables son \(x\) y \(y\), y tenemos dos coeficientes, \(a\) y \(b\).4 El coeficiente a representa la intersección de y de la recta, y el coeficiente b representa la pendiente de la recta. Profundizando más en nuestros recuerdos decadentes de la escuela secundaria (lo siento, para algunas de nosotras la escuela secundaria fue hace mucho tiempo), recordamos que la intersección se interpreta como “el valor de y que obtienes cuando \(x = 0\)”. De manera similar, una pendiente de b significa que si aumentas el valor de x en 1 unidad, entonces el valor de y sube b unidades, y una pendiente negativa significa que el valor de y bajaría en lugar de subir. Ah, sí, ahora me acuerdo de todo. Ahora que lo hemos recordado no debería sorprendernos descubrir que usamos exactamente la misma fórmula para una recta de regresión. Si \(Y\) es la variable de resultado (la VD) y X es la variable predictora (la \(VI\)), entonces la fórmula que describe nuestra regresión se escribe así
\[\hat{Y}_i=b_0+b_1X_i\]
Mmm. Parece la misma fórmula, pero hay algunas partes extra en esta versión. Asegurémonos de entenderlos. En primer lugar, fíjate que he escrito \(X_i\) y \(Y_i\) en lugar de simplemente \(X\) y \(Y\). Esto se debe a que queremos recordar que estamos tratando con datos reales. En esta ecuación, \(X_i\) es el valor de la variable predictora para la i-ésima observación (es decir, la cantidad de horas de sueño que dormí el día i de mi pequeño estudio), y \(Y_i\) es el valor correspondiente de la variable de resultado (es decir, mi mal humor ese día). Y aunque no lo he dicho explícitamente en la ecuación, lo que estamos asumiendo es que esta fórmula funciona para todas las observaciones en el conjunto de datos (es decir, para todo i). En segundo lugar, observa que escribí \(\hat{Y}_i\) y no \(Y_i\) . Esto se debe a que queremos hacer la distinción entre los datos reales \(Y_i\) y la estimación \(\hat{Y}_i\) (es decir, la predicción que hace nuestra recta de regresión). En tercer lugar, cambié las letras utilizadas para describir los coeficientes de a y \(b\) a \(b_0\) y \(b_1\). Así es como a los estadísticos les gusta referirse a los coeficientes en un modelo de regresión. No tengo ni idea de por qué eligieron b, pero eso es lo que hicieron. En cualquier caso, \(b_0\) siempre se refiere al término de intersección y \(b_1\) se refiere a la pendiente.
Excelente, excelente. A continuación, no puedo dejar de notar que, independientemente de si estamos hablando de la recta de regresión buena o mala, los datos no caen perfectamente en la recta. O, dicho de otra forma, los datos \(Y_i\) no son idénticos a las predicciones del modelo de regresión \(\hat{Y}_i\). Dado que a los estadísticos les encanta adjuntar letras, nombres y números a todo, nos referiremos a la diferencia entre la predicción del modelo y ese punto de datos real como un valor residual, y lo llamaremos \(\epsilon_i\).5 En términos matemáticos, los residuales se definen como
\[\epsilon_i=Y_i-\hat{Y}_i\]
lo que a su vez significa que podemos escribir el modelo de regresión lineal completo como
\[Y_i=b_0+b_1X_i+\epsilon_i\]
12.4 Estimación de un modelo de regresión lineal
Bien, ahora volvamos a dibujar nuestras imágenes, pero esta vez agregaré algunas líneas para mostrar el tamaño del residual para todas las observaciones. Cuando la recta de regresión es buena, nuestros residuales (las longitudes de las líneas negras continuas) son bastante pequeñas, como se muestra en Figure 12.12 (a), pero cuando la recta de regresión es mala, los residuales son mucho más grandes, como puedes ver en Figure 12.12 (b). Mmm. Tal vez lo que “queremos” en un modelo de regresión son residuales pequeños. Sí, eso tiene sentido. De hecho, creo que me atreveré a decir que la recta de regresión de “mejor ajuste” es la que tiene los residuales más pequeños. O, mejor aún, dado que a los estadísticos parece gustarles sacar cuadrados de todo, ¿por qué no decir eso?
Los coeficientes de regresión estimados, \(\hat{b}_0\) y \(\hat{b}_1\), son aquellos que minimizan la suma de los residuales al cuadrado, que podemos escribir como \(\sum_i (Y_i - \hat{ Y}_i)^2\) o como \(\sum_i \epsilon_i^2\).

Sí, sí, eso suena aún mejor. Y como lo he marcado así, probablemente signifique que esta es la respuesta correcta. Y dado que esta es la respuesta correcta, probablemente valga la pena tomar nota del hecho de que nuestros coeficientes de regresión son estimaciones (¡estamos tratando de adivinar los parámetros que describen una población!), razón por la cual agregué los sombreritos, para que obtengamos \(\hat{b}_0\) y \(\hat{b}_1\) en lugar de \(b_0\) y \(b_1\). Finalmente, también debo señalar que, dado que en realidad hay más de una forma de estimar un modelo de regresión, el nombre más técnico para este proceso de estimación es regresión de mínimos cuadrados ordinarios (OLS, por sus siglas en inglés).
En este punto, ahora tenemos una definición concreta de lo que cuenta como nuestra “mejor” elección de coeficientes de regresión, \(\hat{b}_0\) y \(\hat{b}_1\). La pregunta natural a hacer a continuación es, si nuestros coeficientes de regresión óptimos son aquellos que minimizan la suma de los residuales al cuadrado, ¿cómo encontramos estos maravillosos números? La respuesta a esta pregunta es complicada y no te ayuda a entender la lógica de la regresión.6 Esta vez te voy a dejar libre. En lugar de mostrarte primero el camino largo y tedioso y luego “revelarte” el maravilloso atajo que ofrece jamovi, vayamos directo al grano y usemos jamovi para hacer todo el trabajo pesado.
12.4.1 Regresión lineal en jamovi
Para ejecutar mi regresión lineal, abre el análisis ‘Regresión’ - ‘Regresión lineal’ en jamovi, utilizando el archivo de datos parenthood.csv. Luego especifica dani.grump como la ‘Variable dependiente’ y dani.sleep como la variable ingresada en el cuadro ‘Covariables’. Esto da los resultados que se muestran en Figure 12.13, mostrando una intersección \(\hat{b}_0 = 125,96\) y la pendiente \(\hat{b}_1 = -8,94\). En otras palabras, la recta de regresión de mejor ajuste que tracé en Figure 12.11 tiene esta fórmula:
\[\hat{Y}_i=125,96+(-8,94 X_i)\]
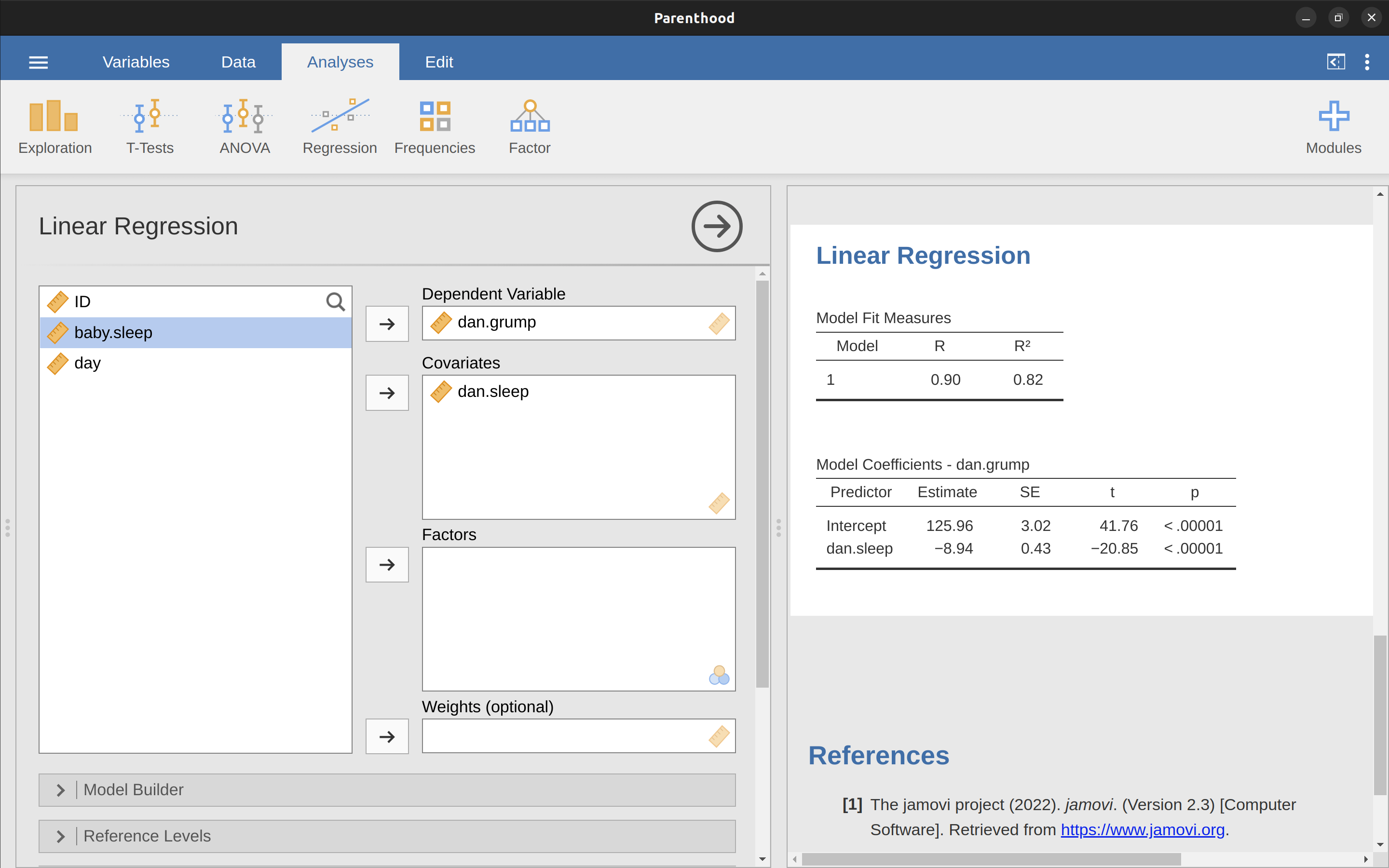
12.4.2 Interpretando el modelo estimado
Lo más importante es entender cómo interpretar estos coeficientes. Comencemos con \(\hat{b}_1\), la pendiente. Si recordamos la definición de la pendiente, un coeficiente de regresión de \(\hat{b}_1 = -8.94\) significa que si aumento Xi en 1, entonces estoy disminuyendo Yi en 8.94. Es decir, cada hora adicional de sueño que gane mejorará mi estado de ánimo, reduciendo mi mal humor en 8,94 puntos de mal humor. ¿Qué pasa con la intersección? Bueno, dado que \(\hat{b}_0\) corresponde al “valor esperado de \(Y_i\) cuando \(X_i\) es igual a 0”, es bastante sencillo. Implica que si duermo cero horas (\(X_i = 0\)), entonces mi mal humor se saldrá de la escala, a un valor insano de (\(Y_i = 125.96\)). Creo que es mejor evitarlo.
12.5 Regresión lineal múltiple
El modelo de regresión lineal simple que hemos discutido hasta este punto asume que hay una sola variable predictora que te interesa, en este caso dani.sleep. De hecho, hasta este punto, todas las herramientas estadísticas de las que hemos hablado han asumido que tu análisis utiliza una variable predictora y una variable de resultado. Sin embargo, en muchos (quizás la mayoría) de los proyectos de investigación, en realidad tienes múltiples predictores que deseas examinar. Si es así, sería bueno poder extender el marco de regresión lineal para poder incluir múltiples predictores. ¿Quizás sería necesario algún tipo de modelo de regresión múltiple?
La regresión múltiple es conceptualmente muy sencilla. Todo lo que hacemos es agregar más términos a nuestra ecuación de regresión. Supongamos que tenemos dos variables que nos interesan; quizás queramos usar tanto dani.sleep como baby.sleep para predecir la variable dani.grump. Como antes, hacemos que \(Y_{i}\) se refiera a mi mal humor en el i-ésimo día. Pero ahora tenemos dos variables $ X $: la primera corresponde a la cantidad de sueño que dormí y la segunda corresponde a la cantidad de sueño que durmió mi hijo. Así que dejaremos que \(X_{i1}\) se refiera a las horas que dormí el i-ésimo día y \(X_{i2}\) se refiera a las horas que durmió el bebé ese día. Si es así, entonces podemos escribir nuestro modelo de regresión así:
\[Y_i=b_0+b_1X_{i1}+b_2X_{i2}+\epsilon_i\]
Como antes, \(\epsilon_i\) es el residual asociado con la i-ésima observación, \(\epsilon_i = Y_i - \hat{Y}_i\). En este modelo, ahora tenemos tres coeficientes que deben estimarse: b0 es la intersección, b1 es el coeficiente asociado con mi sueño y b2 es el coeficiente asociado con el sueño de mi hijo. Sin embargo, aunque el número de coeficientes que deben estimarse ha cambiado, la idea básica de cómo funciona la estimación no ha cambiado: nuestros coeficientes estimados \(\hat{b}_0\), \(\hat{b}_1\) y \(\hat {b}_2\) son los que minimizan la seuma de los residuales al cuadrado.
12.5.1 Haciéndolo en jamovi
La regresión múltiple en jamovi no es diferente a la regresión simple. Todo lo que tenemos que hacer es agregar variables adicionales al cuadro ‘Covariables’ en jamovi. Por ejemplo, si queremos usar dani.sleep y baby.sleep como predictores en nuestro intento de explicar por qué estoy tan malhumorado, entonces mueve baby.sleep al cuadro ‘Covariables’ junto a dani.sleep. Por defecto, jamovi asume que el modelo debe incluir una intersección. Los coeficientes que obtenemos esta vez se muestran en Table 12.4.
| (Intercept) | dani.sleep | baby.sleep |
|---|---|---|
| 125.97 | -8.95 | 0.01 |
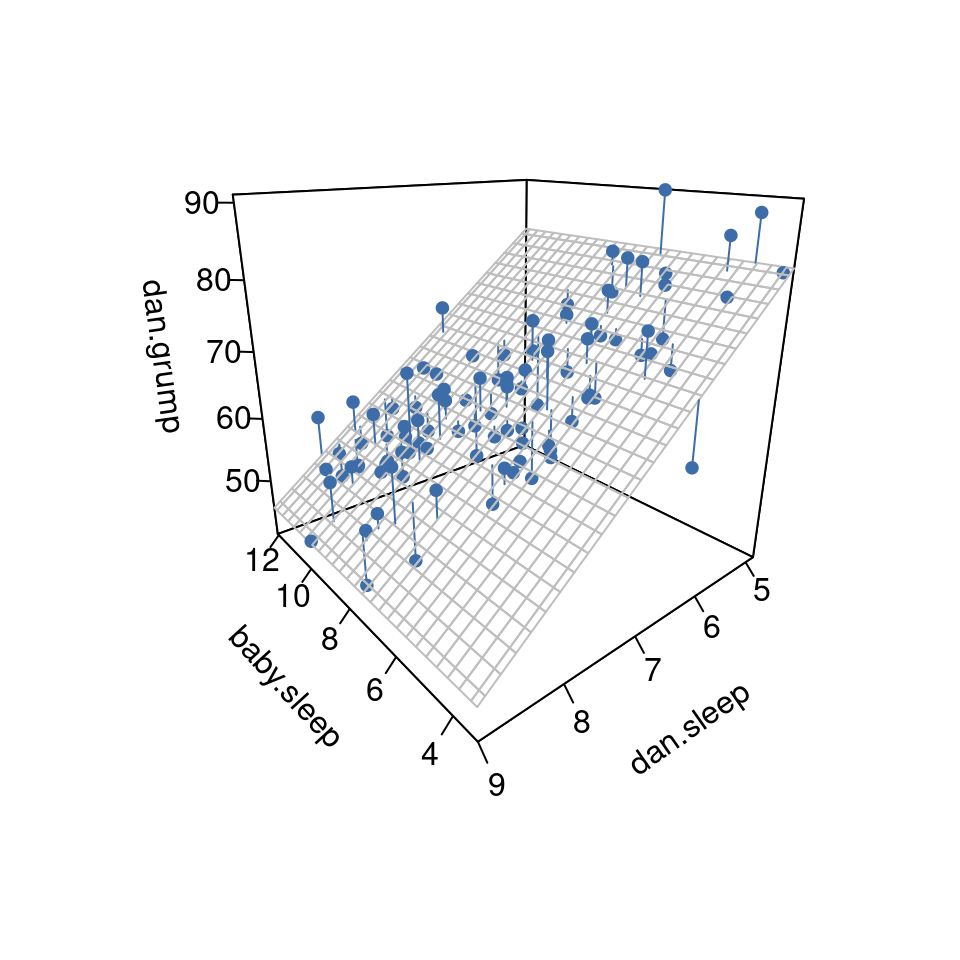
El coeficiente asociado con dani.sleep es bastante grande, lo que sugiere que cada hora de sueño que pierdo me vuelve mucho más gruñona. Sin embargo, el coeficiente de sueño del bebé es muy pequeño, lo que sugiere que en realidad no importa cuánto duerma mi hijo. Lo que importa en cuanto a mi mal humor es cuánto duermo. Para tener una idea de cómo es este modelo de regresión múltiple, Figure 12.14 muestra un gráfico 3D que representa las tres variables, junto con el propio modelo de regresión.
[Detalle técnico adicional7]
12.6 Cuantificando el ajuste del modelo de regresión
Ahora sabemos cómo estimar los coeficientes de un modelo de regresión lineal. El problema es que aún no sabemos si este modelo de regresión es bueno. Por ejemplo, el modelo de regresión.1 afirma que cada hora de sueño mejorará bastante mi estado de ánimo, pero podría ser una tontería. Recuerda, el modelo de regresión solo produce una predicción \(\hat{Y}_i\) sobre cómo es mi estado de ánimo, pero mi estado de ánimo real es \(Y_i\). Si estos dos están muy cerca, entonces el modelo de regresión ha hecho un buen trabajo. Si son muy diferentes, entonces ha hecho un mal trabajo.
12.6.1 El valor de \(R^2\)
Una vez más, pongamos un poco de matemática alrededor de esto. En primer lugar, tenemos la suma de los residuales al cuadrado
\[SS_{res}=\sum_i (Y_i-\hat{Y_i})^2\]
que esperamos que sea bastante pequeña. Específicamente, lo que nos gustaría es que sea muy pequeña en comparación con la variabilidad total en la variable de resultado.
\[SS_{tot}=\sum_i(Y_i-\bar{Y})^2\]
Ya que estamos aquí, calculemos estos valores nosotras mismas, aunque no a mano. Usemos algo como Excel u otro programa de hoja de cálculo estándar. Hice esto abriendo el archivo parenthood.csv en Excel y guardándolo como parenthood rsquared.xls para poder trabajar en él. Lo primero que debes hacer es calcular los valores de \(\hat{Y}\), y para el modelo simple que usa solo un único predictor, haríamos lo siguiente:
- crea una nueva columna llamada ‘Y.pred’ usando la fórmula ‘= 125.97 + (-8.94 \(\times\) dani.sleep)’
- calcula el SS(resid) creando una nueva columna llamada ‘(YY.pred)^2’ utilizando la fórmula ’ = (dani.grump - Y.pred)^2 ’.
- Luego, en la parte inferior de esta columna, calcula la suma de estos valores, es decir, ’ sum( ( YY.pred)^2 ) .
- En la parte inferior de la columna dani.grump, calcula el valor medio para dani.grump (NB Excel usa la palabra ‘PROMEDIO’ en lugar de ‘promedio’ en su función).
- Luego crea una nueva columna, llamada ’ (Y - mean(Y))^2 )’ usando la fórmula ’ = (dani.grump - AVERAGE(dani.grump))^2 ’.
- Luego, en la parte inferior de esta columna, calcula la suma de estos valores, es decir, ‘sum( (Y - mean(Y))^2 )’.
- Calcula R.squared escribiendo en una celda en blanco lo siguiente: ‘= 1 - (SS(resid) / SS(tot) )’.
Esto da un valor para \(R^2\) de ‘0.8161018’. El valor \(R^2\), a veces llamado coeficiente de determinación8 tiene una interpretación simple: es la proporción de la varianza en la variable de resultado que puede ser explicada por el predictor. Entonces, en este caso, el hecho de que hayamos obtenido \(R^2 = .816\) significa que el predictor (my.sleep) explica \(81.6\%\) de la varianza del resultado (my.grump).
Naturalmente, no necesitas escribir todos estos comandos en Excel tú misma si deseas obtener el valor de \(R^2\) para tu modelo de regresión. Como veremos más adelante en la sección sobre [Ejecutar las pruebas de hipótesis en jamovi], todo lo que necesitas hacer es especificar esto como una opción en jamovi. Sin embargo, dejemos eso a un lado por el momento. Hay otra propiedad de \(R^2\) que quiero señalar.
12.6.2 La relación entre regresión y correlación
En este punto podemos revisar mi afirmación anterior de que la regresión, en esta forma tan simple que he discutido hasta ahora, es básicamente lo mismo que una correlación. Anteriormente, usamos el símbolo \(r\) para indicar una correlación de Pearson. ¿Podría haber alguna relación entre el valor del coeficiente de correlación \(r\) y el valor de \(R^2\) de la regresión lineal? Por supuesto que la hay: la correlación al cuadrado \(r^2\) es idéntica al valor de \(R^2\) para una regresión lineal con un solo predictor. En otras palabras, ejecutar una correlación de Pearson es más o menos equivalente a ejecutar un modelo de regresión lineal que usa solo una variable predictora.
12.6.3 El valor \(R^2\) ajustado
Una última cosa a señalar antes de continuar. Es bastante común informar de una medida ligeramente diferente del rendimiento del modelo, conocida como “\(R^2\) ajustado”. La razón que subyace al cálculo del valor de \(R^2\) ajustado es la observación de que agregar más predictores al modelo siempre hará que el valor de \(R^2\) aumente (o al menos no disminuya).
[Detalle técnico adicional9]
Este ajuste es un intento de tener en cuenta los grados de libertad. La gran ventaja del valor de \(R^2\) ajustado es que cuando agregas más predictores al modelo, el valor de \(R^2\) ajustado solo aumentará si las nuevas variables mejoran el rendimiento del modelo más de lo esperado por casualidad. La gran desventaja es que el valor ajustado de \(R^2\) no se puede interpretar de la forma elegante en que se puede interpretar \(R^2\). \(R^2\) tiene una interpretación simple como la proporción de varianza en la variable de resultado que se explica por el modelo de regresión. Que yo sepa, no existe una interpretación equivalente para \(R^2\) ajustado.
Entonces, una pregunta obvia es si debes informar \(R^2\) o ajustar \(R^2\). Esto es probablemente una cuestión de preferencia personal. Si te importa más la interpretabilidad, entonces \(R^2\) es mejor. Si te importa más corregir el sesgo, probablemente sea mejor ajustar \(R^2\). Personalmente, prefiero \(R^2\). Mi sensación es que es más importante poder interpretar la medida del rendimiento del modelo. Además, como veremos en Pruebas de hipótesis para modelos de regresión, si te preocupa que la mejora en \(R^2\) que obtienes al agregar un predictor se deba solo al azar y no porque sea un mejor modelo, bueno, tenemos pruebas de hipótesis para eso.
12.7 Pruebas de hipótesis para modelos de regresión
Hasta ahora hemos hablado sobre qué es un modelo de regresión, cómo se estiman los coeficientes de un modelo de regresión y cómo cuantificamos el rendimiento del modelo (el último de estos, por cierto, es básicamente nuestra medida del tamaño del efecto). Lo siguiente de lo que tenemos que hablar es de las pruebas de hipótesis. Hay dos tipos diferentes (pero relacionados) de pruebas de hipótesis de las que debemos hablar: aquellas en las que probamos si el modelo de regresión como un todo está funcionando significativamente mejor que un modelo nulo, y aquellas en las que probamos si un coeficiente de regresión particular es significativamente diferente de cero.
12.7.1 Probando el modelo como un todo
Bien, supongamos que has estimado tu modelo de regresión. La primera prueba de hipótesis que puedes probar es la hipótesis nula de que no existe una relación entre los predictores y el resultado, y la hipótesis alternativa de que los datos se distribuyen exactamente de la manera que predice el modelo de regresión.
[Detalle técnico adicional10]
Veremos mucho más del estadístico F en Chapter 13, pero por ahora solo ten en cuenta que podemos interpretar valores grandes de F como una indicación de que la hipótesis nula está funcionando mal en comparación con la hipótesis alternativa. En un momento te mostraré cómo hacer la prueba en jamovi de la manera más fácil, pero primero echemos un vistazo a las pruebas para los coeficientes de regresión individuales.
12.7.2 Pruebas para coeficientes individuales
La prueba F que acabamos de presentar es útil para comprobar que el modelo en su conjunto funciona mejor que el azar. Si tu modelo de regresión no produce un resultado significativo para la prueba F, probablemente no tengas un modelo de regresión muy bueno (o, muy posiblemente, no tengas muy buenos datos). Sin embargo, mientras que fallar esta prueba es un indicador bastante fuerte de que el modelo tiene problemas, pasar la prueba (es decir, rechazar el valor nulo) no implica que el modelo sea bueno. ¿Por qué ocurre eso, te estarás preguntando? La respuesta se puede encontrar mirando los coeficientes del modelo Regresión lineal múltiple que ya hemos visto (Table 12.4)
No puedo dejar de notar que el coeficiente de regresión estimado para la variable baby.sleep es pequeño (\(0.01\)), en relación al valor que obtenemos para dani.sleep (\(-8.95\)). Dado que estas dos variables están en la misma escala (ambas se miden en “horas dormidas”), me parece que esto es esclarecedor. De hecho, estoy empezando a sospechar que en realidad solo la cantidad de sueño que duermo es lo que importa para predecir mi mal humor. Podemos reutilizar una prueba de hipótesis que discutimos anteriormente, la prueba t. La prueba que nos interesa tiene una hipótesis nula de que el verdadero coeficiente de regresión es cero (\(b = 0\)), que debe probarse contra la hipótesis alternativa de que no lo es (\(b \neq 0\)). Eso es:
\[H_0:b=0\] \[H_1:b \neq 0\]
¿Cómo podemos probar esto? Bueno, si el teorema central del límite es bueno con nosotros, podríamos suponer que la distribución muestral de \(\hat{b}\), el coeficiente de regresión estimado, es una distribución normal con la media centrada en \(b\). Lo que eso significaría es que si la hipótesis nula fuera cierta, entonces la distribución muestral de \(\hat{b}\) tiene una media cero y una desviación estándar desconocida. Suponiendo que podemos llegar a una buena estimación del error estándar del coeficiente de regresión, \(se(\hat{b})\), entonces tenemos suerte. Esa es exactamente la situación para la que introdujimos la prueba t de una muestra en Chapter 11. Así que definamos un estadístico t como este
\[t=\frac{\hat{b}}{SE(\hat{b})}\]
Pasaré por alto las razones, pero nuestros grados de libertad en este caso son \(df = N - K - 1\). De manera irritante, la estimación del error estándar del coeficiente de regresión, \(se(\hat{b})\), no es tan fácil de calcular como el error estándar de la media que usamos para las pruebas t más sencillas en Chapter 11. De hecho, la fórmula es algo fea y no muy útil de ver.11 Para nuestros propósitos, es suficiente señalar que el error estándar del coeficiente de regresión estimado depende de las variables predictoras y de resultado, y es algo sensible a las violaciones del supuesto de homogeneidad de varianzas (discutido en breve).
En cualquier caso, este estadístico t se puede interpretar de la misma manera que los estadísticos t que analizamos en Chapter 11. Suponiendo que tienes una alternativa de dos colas (es decir, no te importa si b \(>\) 0 o b \(<\) 0), entonces son los valores extremos de t (es decir, mucho menos que cero o mucho mayor que cero) que sugieren que debes rechazar la hipótesis nula.
12.7.3 Ejecutando las pruebas de hipótesis en jamovi
Para calcular todos los estadísticos de los que hemos hablado hasta ahora, todo lo que necesitas hacer es asegurarte de que las opciones relevantes estén marcadas en jamovi y luego ejecutar la regresión. Si hacemos eso, como en Figure 12.15, obtenemos una gran cantidad de resultados útiles.

Los ‘Coeficientes del modelo’ en la parte inferior de los resultados del análisis jamovi que se muestran en Figure 12.15 proporcionan los coeficientes del modelo de regresión. Cada fila de esta tabla se refiere a uno de los coeficientes del modelo de regresión. La primera fila es el término de intersección, y las últimas miran cada uno de los predictores. Las columnas te ofrecen toda la información relevante. La primera columna es la estimación real de \(b\) (por ejemplo, \(125,97\) para la intersección y -8,95 para el predictor dani.sleep). La segunda columna es la estimación del error estándar \(\hat{\sigma}_b\). Las columnas tercera y cuarta proporcionan los valores inferior y superior para el intervalo de confianza del 95% alrededor de la estimación b (más sobre esto más adelante). La quinta columna te da el estadístico t, y vale la pena notar que en esta tabla \(t=\frac{\hat{b}} {se({\hat{b}})}\) . Finalmente, la última columna te muestra el valor p real para cada una de estas pruebas.12
Lo único que la tabla de coeficientes en sí no incluye son los grados de libertad utilizados en la prueba t, que siempre es \(N - K - 1\) y se enumeran en la parte superior de la tabla, etiquetada como ‘Medidas de ajuste del modelo’. Podemos ver en esta tabla que el modelo funciona significativamente mejor de lo que cabría esperar por casualidad (\(F(2,97) = 215.24, p< .001\)), lo cual no es tan sorprendente: el valor \(R^2 = .81\) indica que el modelo de regresión representa \(81\%\) de la variabilidad en la medida de resultado (y \(82\%\) para el \(R^2\) ajustado). Sin embargo, cuando volvemos a mirar las pruebas t para cada uno de los coeficientes individuales, tenemos pruebas bastante sólidas de que la variable sueño del bebé no tiene un efecto significativo. Todo el trabajo en este modelo lo realiza la variable dani.sleep. En conjunto, estos resultados sugieren que este modelo de regresión es en realidad el modelo incorrecto para los datos. Probablemente sea mejor que deje por completo el predictor del sueño del bebé. En otras palabras, el modelo de regresión simple con el que comenzamos es el mejor modelo.
12.8 Sobre los coeficientes de regresión
Antes de pasar a discutir los supuestos subyacentes a la regresión lineal y lo que puedes hacer para verificar si se cumplen, hay dos temas más que quiero discutir brevemente, los cuales se relacionan con los coeficientes de regresión. Lo primero de lo que hablar es de calcular los intervalos de confianza para los coeficientes. Después de eso, discutiré la cuestión un tanto turbia de cómo determinar qué predictor es el más importante.
12.8.1 Intervalos de confianza para los coeficientes
Como cualquier parámetro poblacional, los coeficientes de regresión b no pueden estimarse con total precisión a partir de una muestra de datos; eso es parte de por qué necesitamos pruebas de hipótesis. Dado esto, es muy útil poder informar intervalos de confianza que capturen nuestra incertidumbre sobre el verdadero valor de \(b\). Esto es especialmente útil cuando la pregunta de investigación se centra en gran medida en un intento de averiguar la relación entre la variable \(X\) y la variable \(Y\), ya que en esas situaciones el interés está principalmente en el peso de regresión \(b\).
[Detalle técnico adicional13]
En jamovi ya habíamos especificado el ‘intervalo de confianza del 95%’ como se muestra en Figure 12.15, aunque podríamos haber elegido fácilmente otro valor, digamos un ‘intervalo de confianza del 99%’ si eso es lo que decidimos.
12.8.2 Cálculo de coeficientes de regresión estandarizados
Una cosa más que quizás quieras hacer es calcular los coeficientes de regresión “estandarizados”, a menudo denominados \(\beta\). La lógica de los coeficientes estandarizados es la siguiente. En muchas situaciones, tus variables están en escalas diferentes. Supongamos, por ejemplo, que mi modelo de regresión pretende predecir las puntuaciones de \(IQ\) de las personas utilizando su nivel educativo (número de años de educación) y sus ingresos como predictores. Obviamente, el nivel educativo y los ingresos no están en la misma escala. La cantidad de años de escolaridad solo puede variar en decenas de años, mientras que los ingresos pueden variar en $ 10,000 dólares (o más). Las unidades de medida tienen una gran influencia en los coeficientes de regresión. Los coeficientes b solo tienen sentido cuando se interpretan a la luz de las unidades, tanto de las variables predictoras como de la variable resultado. Esto hace que sea muy difícil comparar los coeficientes de diferentes predictores. Sin embargo, hay situaciones en las que realmente deseas hacer comparaciones entre diferentes coeficientes. Específicamente, es posible que quieras algún tipo de medida estándar de qué predictores tienen la relación más fuerte con el resultado. Esto es lo que pretenden hacer los coeficientes estandarizados.
La idea básica es bastante simple; los coeficientes estandarizados son los coeficientes que habrías obtenido si hubieras convertido todas las variables a puntuaciones z antes de ejecutar la regresión.14 La idea aquí es que, al convertir todos los predictores en puntuaciones z, todos entran en la regresión en la misma escala, eliminando así el problema de tener variables en diferentes escalas. Independientemente de cuáles fueran las variables originales, un valor \(\beta\) de 1 significa que un aumento en el predictor de 1 desviación estándar producirá un aumento correspondiente de 1 desviación estándar en la variable de resultado. Por lo tanto, si la variable A tiene un valor absoluto de \(\beta\) mayor que la variable B, se considera que tiene una relación más fuerte con el resultado. O al menos esa es la idea. Vale la pena ser un poco cauteloso aquí, ya que esto depende en gran medida del supuesto de que “un cambio de 1 desviación estándar” es fundamentalmente lo mismo para todas las variables. No siempre es obvio que esto sea cierto.
[Detalle técnico adicional15]
Para simplificar aún más las cosas, jamovi tiene una opción que calcula los coeficientes \(\beta\) por ti usando la casilla de verificación ‘Estimación estandarizada’ en las opciones ‘Coeficientes del modelo’, ver los resultados en Figure 12.16.
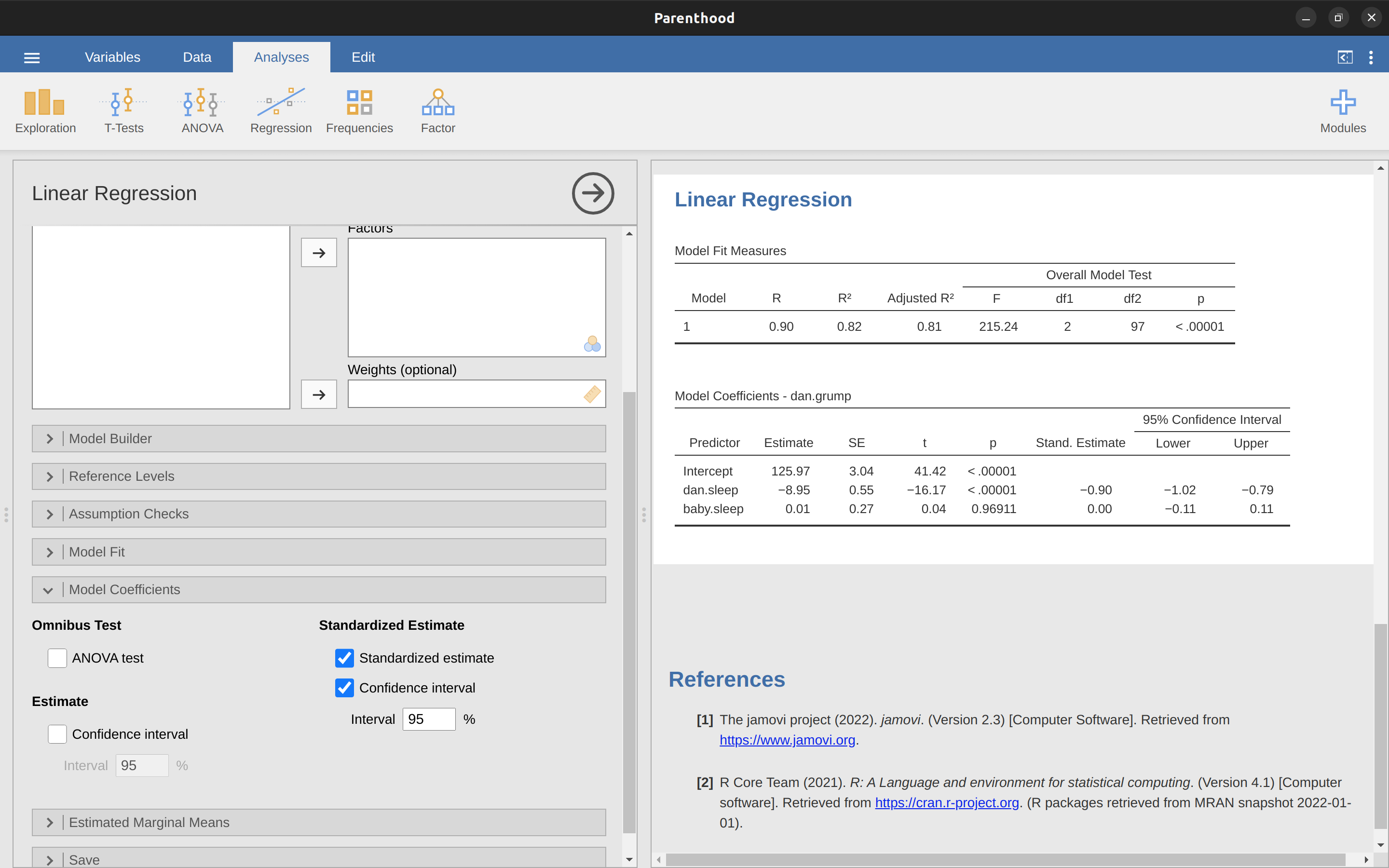
Estos resultados muestran claramente que la variable dani.sleep tiene un efecto mucho más fuerte que la variable baby.sleep. Sin embargo, este es un ejemplo perfecto de una situación en la que probablemente tendría sentido utilizar los coeficientes b originales en lugar de los coeficientes estandarizados \(\beta\). Después de todo, mi sueño y el sueño del bebé ya están en la misma escala: número de horas dormidas. ¿Por qué complicar las cosas al convertirlos en puntuaciones z?
12.9 Supuestos de regresión
El modelo de regresión lineal que he estado discutiendo se basa en varios supuestos. En Comprobación de modelos hablaremos mucho más sobre cómo comprobar que se cumplen estos supuestos, pero primero echemos un vistazo a cada uno de ellos.
- Linealidad. Un supuesto bastante fundamental del modelo de regresión lineal es que la relación entre \(X\) y \(Y\) en realidad es lineal. Independientemente de si se trata de una regresión simple o una regresión múltiple, asumimos que las relaciones involucradas son lineales.
- Independencia: los residuales son independientes entre sí. En realidad, se trata de un supuesto general, en el sentido de que “no hay nada raro en los residuales”. Si ocurre algo extraño (p. ej., todos los residuales dependen en gran medida de alguna otra variable no medida), podría estropear las cosas. La independencia no es algo que puedas verificar directa y específicamente con herramientas de diagnóstico, pero si tus diagnósticos de regresión están en mal estado, piensa detenidamente en la independencia de tus observaciones y residuales.
- Normalidad. Como muchos de los modelos en estadística, la regresión lineal simple o múltiple básica se basa en un supuesto de normalidad. Específicamente, asume que los residuales se distribuyen normalmente. En realidad, está bien si los predictores \(X\) y las variables de resultado \(Y\) no son normales, siempre que los residuales \(\epsilon\) sean normales. Consulta la sección [Comprobación de la normalidad de los residuos].
- Ecalidad (u ‘homogeneidad’) de la varianza. Estrictamente hablando, el modelo de regresión asume que cada residual \(\epsilon_i\) se genera a partir de una distribución normal con media 0 y (más importante para los propósitos actuales) con una desviación estándar \(\sigma\) que es la misma para cada residual. En la práctica, es imposible probar el supuesto de que todos los residuales se distribuyen de manera idéntica. En cambio, lo que nos interesa es que la desviación estándar del residual sea la misma para todos los valores de \(\hat{Y}\) y (si somos especialmente diligentes) para todos los valores de cada predictor \(X\) en el modelo.
Entonces, tenemos cuatro supuestos principales para la regresión lineal (que forman claramente el acrónimo ‘LINE’). Y además hay un par de cosas que también debemos verificar:
- Predictores no correlacionados. La idea aquí es que, en un modelo de regresión múltiple, no deseas que tus predictores estén demasiado correlacionados entre sí. Esto no es “técnicamente” un supuesto del modelo de regresión, pero en la práctica es necesario. Los predictores que están demasiado correlacionados entre sí (lo que se conoce como “colinealidad”) pueden causar problemas al evaluar el modelo. Consulta la sección Comprobación de la colinealidad.
- No hay valores atípicos “malos”. Nuevamente, en realidad no es un supuesto técnico del modelo (o más bien, está implícito en todos los demás), pero hay un supuesto implícito de que tu modelo de regresión no está muy influenciado por uno o dos puntos de datos anómalos porque esto plantea dudas sobre la idoneidad del modelo y la fiabilidad de los datos en algunos casos. Consulta la sección sobre Datos atípicos y anómalos.
12.10 Comprobación del modelo
Esta sección se centra en el diagnóstico de regresión, un término que se refiere al arte de verificar que se hayan cumplido los supuestos de tu modelo de regresión, descubrir cómo arreglar el modelo si se violan los supuestos y, en general, comprobar que no pasa nada “raro”. Me refiero a esto como el “arte” de la verificación de modelos por una buena razón. No es fácil, y aunque hay muchas herramientas fácilmente disponibles que puedes usar para diagnosticar y tal vez incluso arreglar los problemas que afectan a tu modelo (si es que hay alguno), realmente hay que tener cierto criterio al hacerlo.
En esta sección, describo varias cosas diferentes que puedes hacer para comprobar que tu modelo de regresión está haciendo lo que se supone que debe hacer. No cubre todas las cosas que podrías hacer, pero aún así es mucho más detallado de lo que se hace a menudo en la práctica, desafortunadamente. Pero es importante que tengas una idea de las herramientas que tienes a tu disposición, así que trataré de presentar algunas de ellas aquí. Finalmente, debo señalar que esta sección se basa en gran medida en @ Fox2011, el libro asociado con el paquete ‘car’ que se usa para realizar análisis de regresión en R. El paquete ‘car’ se destaca por proporcionar algunas herramientas excelentes para el diagnóstico de regresión, y el libro mismo habla de ellos de una manera admirablemente clara. No quiero sonar demasiado efusiva al respecto, pero creo que vale la pena leer @ Fox2011, incluso si algunas de las técnicas de diagnóstico avanzadas solo están disponibles en R y no en jamovi.
12.10.1 Tres tipos de residuales
La mayoría de los diagnósticos de regresión giran en torno a la observación de los residuales, y existen varios tipos diferentes de residuales que podríamos considerar. En particular, en esta sección se hace referencia a los siguientes tres tipos de residuales: “residuales ordinarios”, “residuales estandarizados” y “residuales estudentizados”. Hay un cuarto tipo al que verás que se hace referencia en algunas de las Figuras, y ese es el “residual de Pearson”. Sin embargo, para los modelos de los que estamos hablando en este capítulo, el residual de Pearson es idéntico al residual ordinario.
El primer y más simple tipo de residuales que nos interesan son los residuales ordinarios. Estos son los residuales brutos reales de los que he estado hablando a lo largo de este capítulo hasta ahora. El residual ordinario es simplemente la diferencia entre el valor predicho \(\hat{Y}_i\) y el valor observado \(Y_i\). He estado usando la notación \(\epsilon_i\) para referirme al residual ordinario i-ésimo y así, con esto en mente, tenemos la ecuación muy simple
\[\epsilon_i=Y_i-\hat{Y_i}\]
Por supuesto, esto es lo que vimos antes y, a menos que me refiera específicamente a algún otro tipo de residual, este es del que estoy hablando. Así que no hay nada nuevo aquí. Solo quería repetirme. Una desventaja de usar residuales ordinarios es que siempre están en una escala diferente, dependiendo de cuál sea la variable de resultado y cómo de bueno sea el modelo de regresión. Es decir, a menos que hayas decidido ejecutar un modelo de regresión sin un término de intersección, los residuales ordinarios tendrán media 0 pero la varianza es diferente para cada regresión. En muchos contextos, especialmente donde solo estás interesada en el patrón de los residuales y no en sus valores reales, es conveniente estimar los residuales estandarizados, que se normalizan de tal manera que tienen una desviación estándar de 1.
[Detalle técnico adicional16]
El tercer tipo de residuales son los residuales estudentizados (también llamados “residuales jackknifed”) y son incluso más sofisticados que los residuales estandarizados. Nuevamente, la idea es coger el residuo ordinario y dividirlo por alguna cantidad para estimar alguna noción estandarizada del residual. 17
Antes de continuar, debo señalar que a menudo no es necesario obtener estos residuales por ti misma, a pesar de que son la base de casi todos los diagnósticos de regresión. La mayoría de las veces, las diversas opciones que proporcionan los diagnósticos, o las comprobaciones de supuestos, se encargarán de estos cálculos por ti. Aun así, siempre es bueno saber cómo obtener estas cosas tú misma en caso de que alguna vez necesites hacer algo no estándar.
12.10.2 Verificando la linealidad de la relación
Deberíamos verificar la linealidad de las relaciones entre los predictores y los resultados. Hay diferentes cosas que podrías hacer para verificar esto. En primer lugar, nunca está de más trazar la relación entre los valores predichos \(\hat{Y}_i\) y los valores observados \(Y_i\) para la variable de resultado, como se ilustra en Figure 12.17. Para dibujar esto en jamovi, guardamos los valores predichos en el conjunto de datos y luego dibujamos un diagrama de dispersión de los valores observados contra los predichos (ajustados). Esto te da una especie de “vista general”: si este gráfico se ve aproximadamente lineal, entonces probablemente no lo estemos haciendo tan mal (aunque eso no quiere decir que no haya problemas). Sin embargo, si puedes ver grandes desviaciones de la linealidad aquí, entonces sugiere que necesitas hacer algunos cambios.
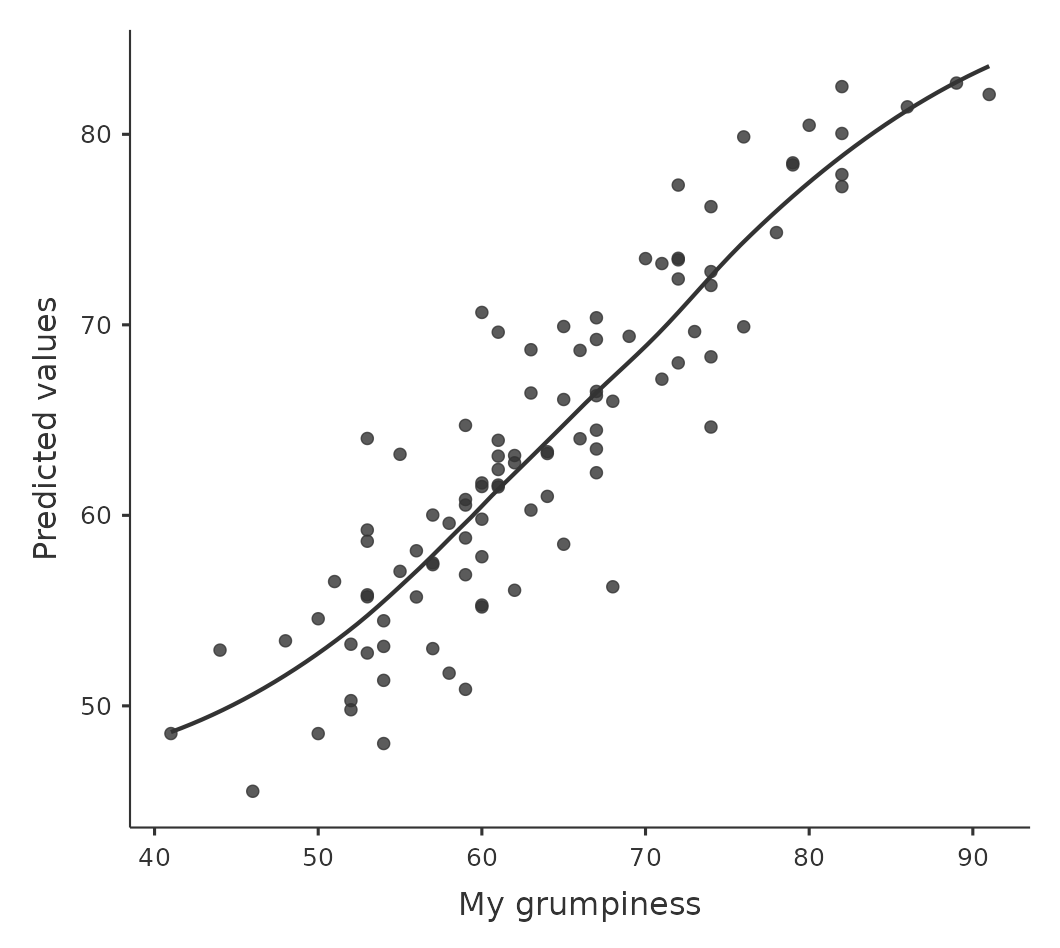
En cualquier caso, para obtener una imagen más detallada, a menudo es más informativo observar la relación entre los valores pronosticados y los residuales mismos. Nuevamente, en jamovi puedes guardar los residuales en el conjunto de datos y luego dibujar un diagrama de dispersión de los valores pronosticados contra los valores residuales, como en Figure 12.18. Como puedes ver, no solo dibuja el diagrama de dispersión que muestra el valor pronosticado contra los residuales, sino que también puede trazar una línea a través de los datos que muestra la relación entre los dos. Idealmente, debería ser una línea recta y perfectamente horizontal. En la práctica, buscamos una línea razonablemente recta o plana. Es una cuestión de criterio.

Se producen versiones algo más avanzadas del mismo gráfico al marcar ‘Gráficos de residuales’ en las opciones de análisis de regresión ‘Comprobaciones de supuestos’ en jamovi. Estos son útiles no solo para verificar la linealidad, sino también para verificar la normalidad y el supuesto de homogeneidad de varianzas, y los analizamos con más detalle en Section 12.10.3. Esta opción no solo dibuja gráficos que comparan los valores pronosticados con los residuales, sino que también lo hace para cada predictor individual.
12.10.3 Comprobación de la normalidad de los residuales
Como muchas de las herramientas estadísticas que hemos discutido en este libro, los modelos de regresión se basan en un supuesto de normalidad. En este caso, asumimos que los residuales se distribuyen normalmente. Lo primero que podemos hacer es dibujar un gráfico QQ a través de la opción ‘Comprobaciones de supuestos’ - ‘Comprobaciones de supuestos’ - ‘Gráfico QQ de residuales’. El resultado se muestra en Figure 12.19, que muestra los residuales estandarizados representados en función de sus cuantiles teóricos según el modelo de regresión.
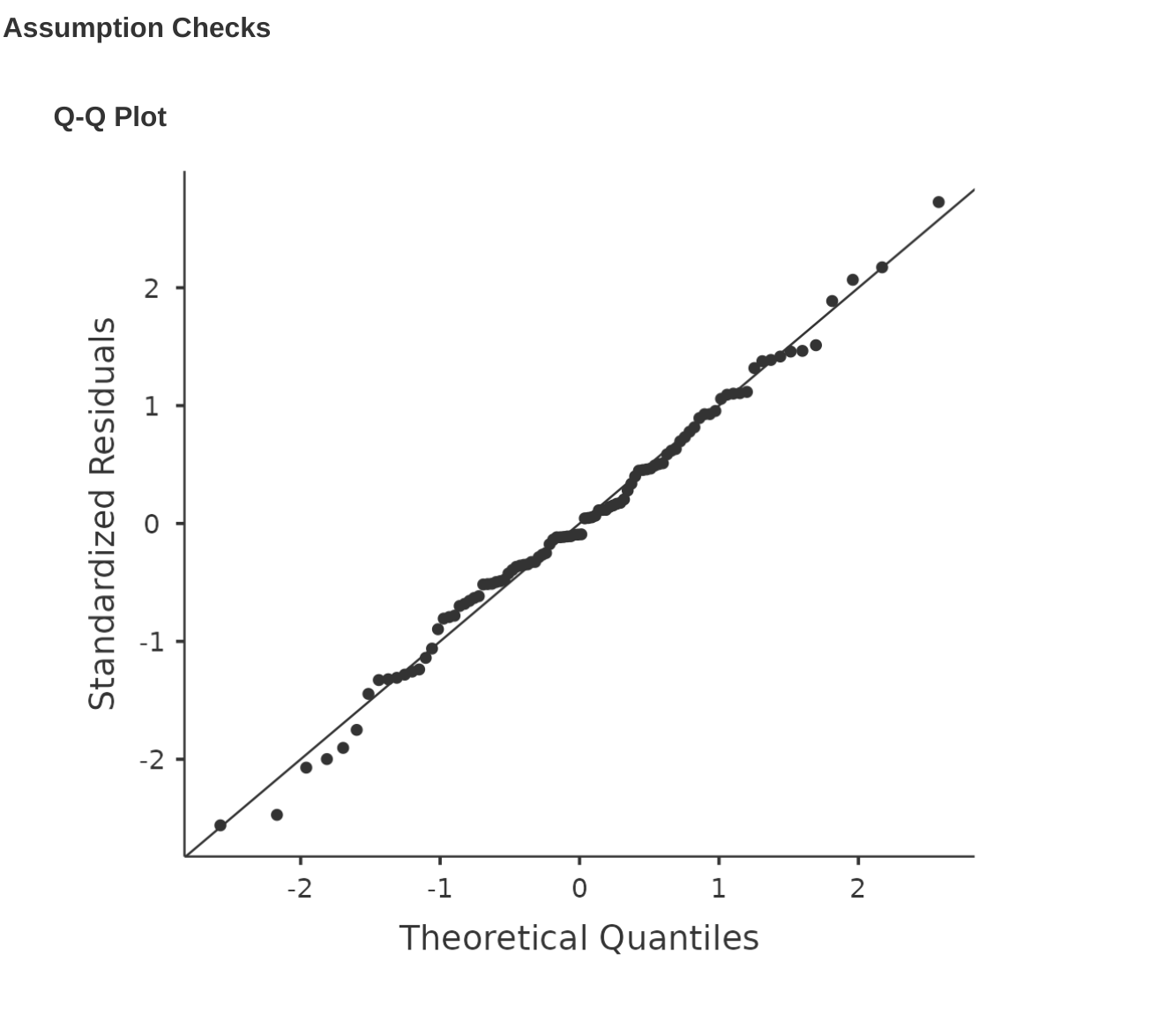
Otra cosa que debemos comprobar es la relación entre los valores predichos (ajustados) y los propios residuales. Podemos hacer que jamovi lo haga usando la opción ‘Gráficos de residuales’, que proporciona un gráfico de dispersión para cada variable predictora, la variable de resultado y los valores pronosticados frente a los residuales, ver Figure 12.20. En estos gráficos buscamos una distribución bastante uniforme de los ‘puntos’, sin agrupamientos ni patrones claros de los ‘puntos’. Observando estos gráficos, no hay nada especialmente preocupante, ya que los puntos están distribuidos de manera bastante uniforme por todo el gráfico. Puede haber un poco de falta de uniformidad en el gráfico (b), pero no es una desviación importante y probablemente no valga la pena preocuparse.

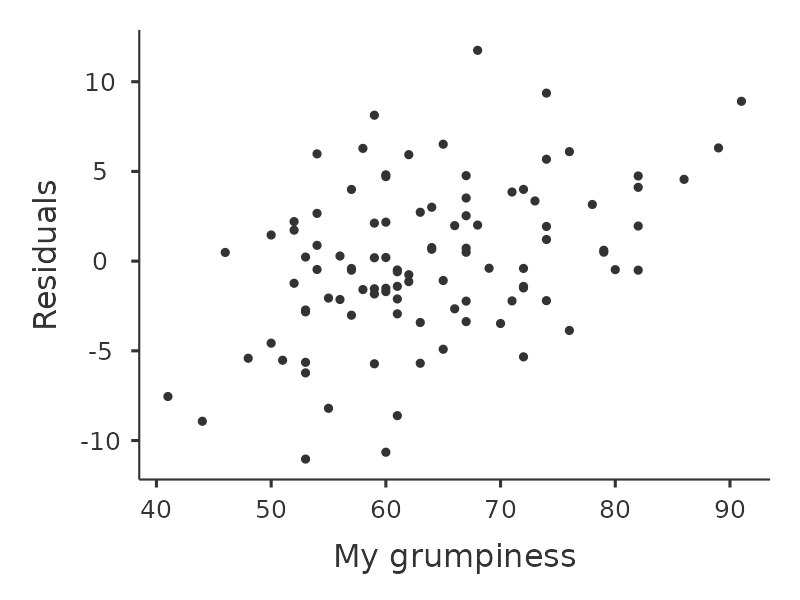
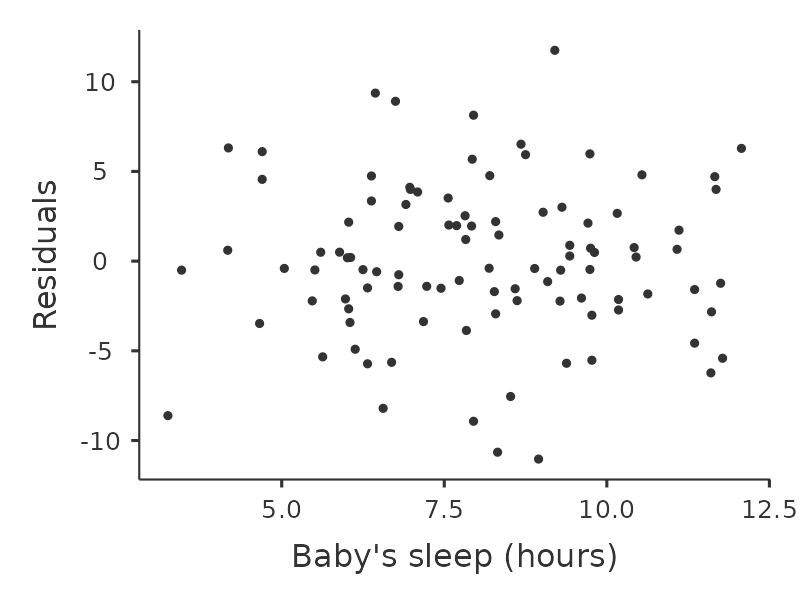
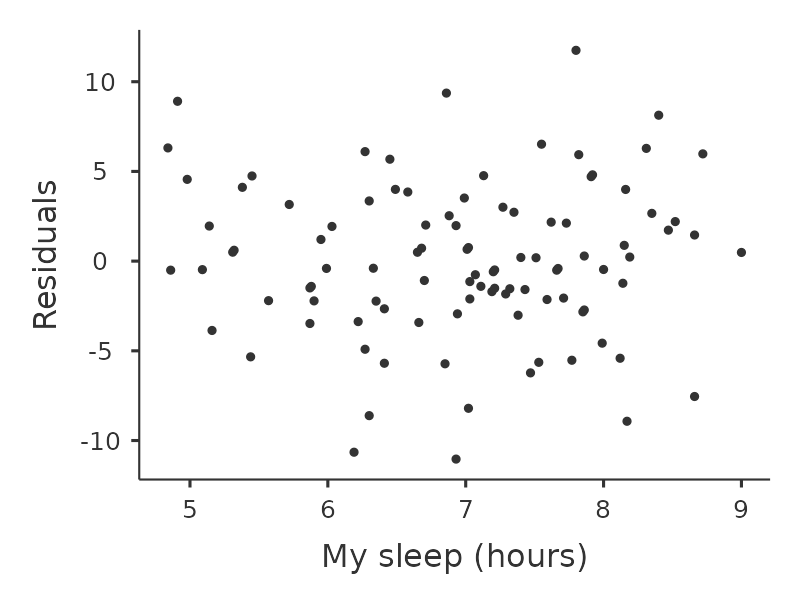
Si estábamos preocupadas, en muchos casos la solución a este problema (y muchos otros) es transformar una o más de las variables. Discutimos los conceptos básicos de la transformación de variables en Section 6.3, pero quiero hacer una nota especial de una posibilidad adicional que no expliqué completamente antes: la transformación de Box-Cox. La función Box-Cox es bastante simple y se usa mucho. 18
Puedes calcularlo usando la función BOXCOX en la pantalla de variables ‘Calcular’ en jamovi.
12.10.4 Comprobación de la igualdad de varianzas
Todos los modelos de regresión de los que hemos hablado hacen un supuesto de igualdad (es decir, homogeneidad) de la varianza: se supone que la varianza de los residuales es constante. Para representar esto gráficamente en jamovi primero necesitamos calcular la raíz cuadrada del tamaño (absoluto) del residual19 y luego representar esto contra los valores predichos, como en Figure 12.21. Ten en cuenta que este gráfico en realidad usa los residuales estandarizados en lugar de los brutos, pero es irrelevante desde nuestro punto de vista. Lo que queremos ver aquí es una línea recta horizontal que atraviesa el centro de la gráfica.20

12.10.5 Comprobación de la colinealidad
Otro diagnóstico de regresión lo proporcionan los factores de inflación de varianza (FIV), que son útiles para determinar si los predictores en tu modelo de regresión están demasiado correlacionados entre sí o no. Hay un factor de inflación de varianza asociado con cada predictor \(X_k\) en el modelo. 21
Si solo tienes dos predictores, los valores de FIV siempre serán los mismos, como podemos ver si hacemos clic en la casilla de verificación ‘Colinealidad’ en las opciones ‘Regresión’ - ‘Supuestos’ en jamovi. Tanto para dani.sleep como para baby.sleep el FIV es de \(1.65\). Y dado que la raíz cuadrada de \(1.65\) es \(1.28\), vemos que la correlación entre nuestros dos predictores no está causando mucho problema.
Para dar una idea de cómo podríamos terminar con un modelo que tiene mayores problemas de colinealidad, supongamos que tuvieras que ejecutar un modelo de regresión mucho menos interesante, en el que intentaras predecir el día en que se recogieron los datos, en función de todas las demás variables en el conjunto de datos. Para ver por qué esto sería un pequeño problema, echemos un vistazo a la matriz de correlación para las cuatro variables (Figure 12.22).

¡Tenemos algunas correlaciones bastante grandes entre algunas de nuestras variables predictoras! Cuando ejecutamos el modelo de regresión y observamos los valores FIV, vemos que la colinealidad está causando mucha incertidumbre sobre los coeficientes. Primero, ejecuta la regresión, como en Figure 12.23 y puedes ver a partir de los valores FIV que, sí, ahí hay una colinealidad muy fina.
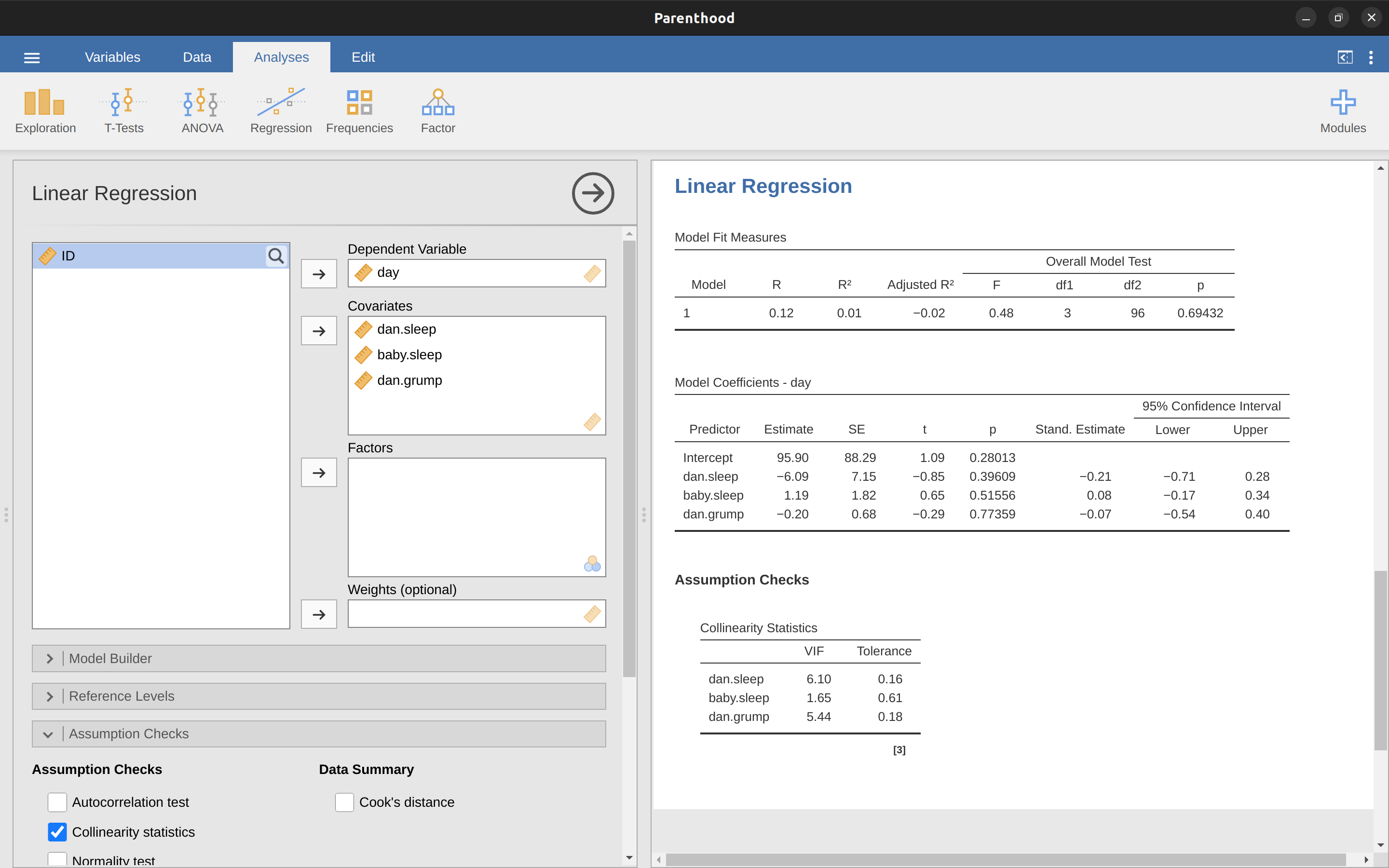
12.10.6 Datos atípicos y anómalos
Un peligro con el que puedes encontrarte con los modelos de regresión lineal es que tu análisis puede ser desproporcionadamente sensible a un pequeño número de observaciones “inusuales” o “anómalas”. Discutí esta idea anteriormente en Section 5.2.3 cuando comenté los valores atípicos que se identifican automáticamente mediante la opción de diagrama de caja en ‘Exploración’ - ‘Descriptivos’, pero esta vez necesitamos ser mucho más precisas. En el contexto de la regresión lineal, hay tres formas conceptualmente distintas en las que una observación puede llamarse “anómala”. Las tres son interesantes, pero tienen implicaciones bastante diferentes para tu análisis.
El primer tipo de observación inusual es un valor atípico. La definición de un valor atípico (en este contexto) es una observación que es muy diferente de lo que predice el modelo de regresión. Se muestra un ejemplo en Figure 12.24. En la práctica, operacionalizamos este concepto diciendo que un valor atípico es una observación que tiene un residual muy grande, \(\epsilon_i^*\). Los valores atípicos son interesantes: un valor atípico grande puede corresponder a datos basura, por ejemplo, las variables pueden haberse registrado incorrectamente en el conjunto de datos, o puede detectarse algún otro defecto. Ten en cuenta que no debes descartar una observación solo porque es un valor atípico. Pero el hecho de que sea un caso atípico es a menudo una señal para mirar con más de talle ese caso y tratar de descubrir por qué es tan diferente.

La segunda forma en que una observación puede ser inusual es si tiene un alto apalancamiento, lo que sucede cuando la observación es muy diferente de todas las demás observaciones. Esto no necesariamente tiene que corresponder a un residual grande. Si la observación resulta ser inusual en todas las variables precisamente de la misma manera, en realidad puede estar muy cerca de la línea de regresión. Un ejemplo de esto se muestra en Figure 12.24. El apalancamiento de una observación se operacionaliza en términos de su valor sombrero, generalmente escrito \(h_i\). La fórmula para el valor sombrero es bastante complicada22 pero su interpretación no lo es: \(h_i\) es una medida de hasta qué punto la i-ésima observación “controla” hacia dónde se dirige la línea de regresión.
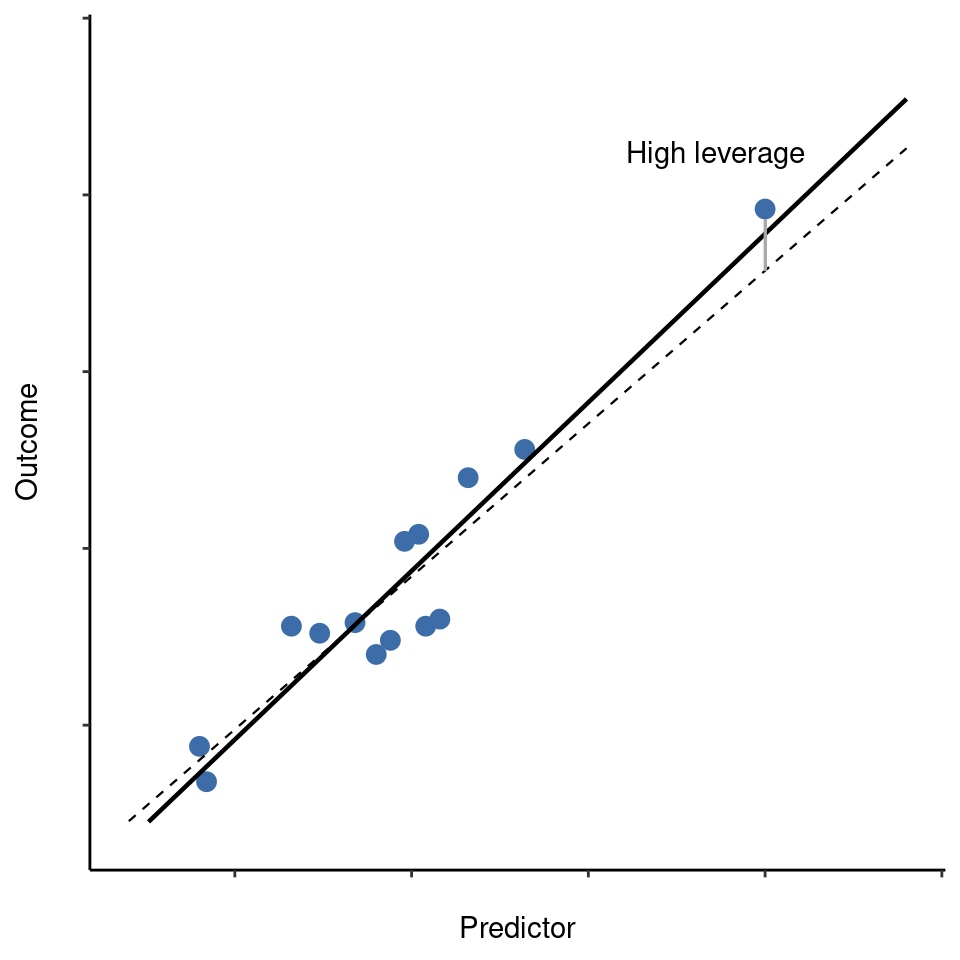
En general, si una observación se encuentra muy alejada de las demás en términos de las variables predictoras, tendrá un valor de sombrero grande (como guía aproximada, la influencia alta es cuando el valor de sombrero es más de 2 o 3 veces el promedio; y ten en cuenta que la suma de los valores sombrero está limitada a ser igual a \(K + 1\)). También vale la pena analizar con más detalle los puntos de alto apalancamiento, pero es mucho menos probable que sean motivo de preocupación a menos que también sean valores atípicos.
Esto nos lleva a nuestra tercera medida de inusualidad, la influencia de una observación. Una observación de alta influencia es un valor atípico que tiene una alta influencia. Es decir, es una observación que es muy diferente a todas las demás en algún aspecto, y también se encuentra muy lejos de la línea de regresión. Esto se ilustra en Figure 12.26. Nota el contraste con las dos figuras anteriores. Los valores atípicos no mueven mucho la línea de regresión y tampoco los puntos de aalta influencia. Pero algo que es un valor atípico y tiene una alta influencia, bueno, eso tiene un gran efecto en la línea de regresión. Por eso llamamos a estos puntos de alta influencia, y es por eso que son la mayor preocupación. Operacionalizamos la influencia en términos de una medida conocida como distancia de Cook. 23
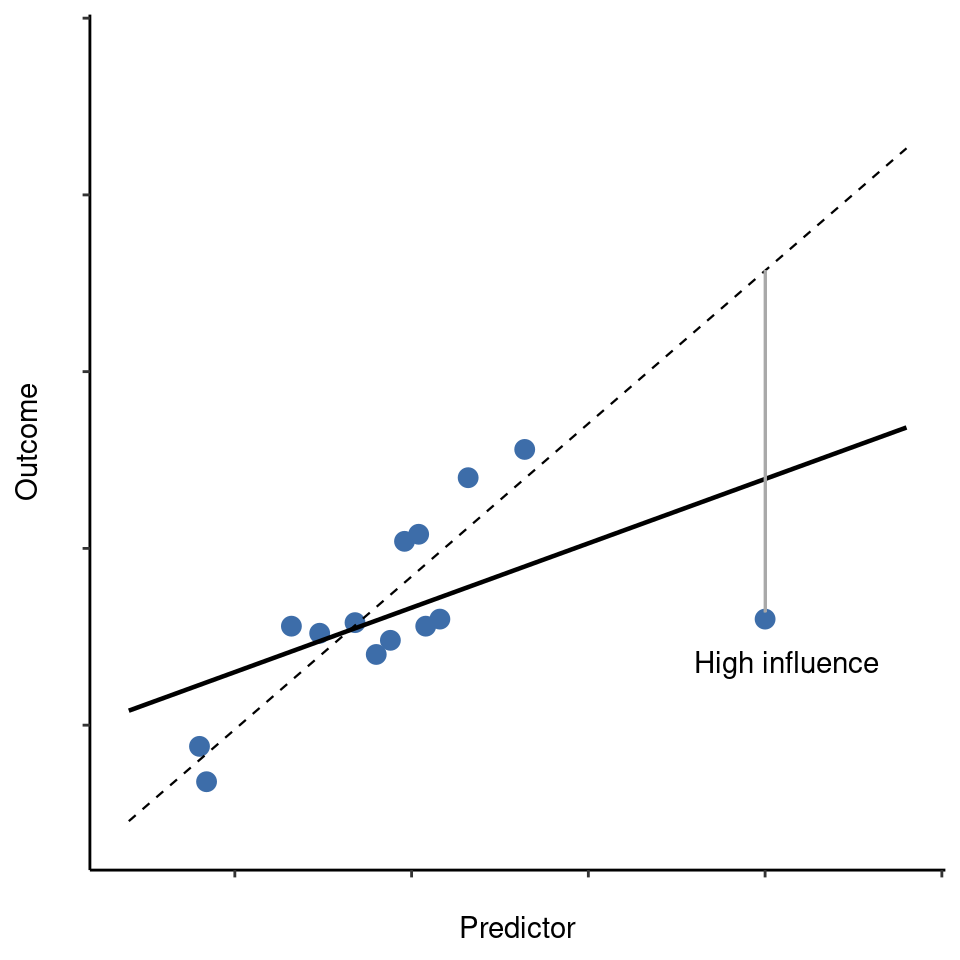
Para tener una distancia de Cook grande, una observación debe ser un valor atípico bastante sustancial y tener una alta influencia. Como guía aproximada, la distancia de Cook superior a 1 a menudo se considera grande (eso es lo que normalmente uso como una regla rápida).
En jamovi, la información sobre la distancia de Cook se puede calcular haciendo clic en la casilla de verificación ‘Distancia de Cook’ en las opciones ‘Comprobaciones de supuestos’ - ‘Resumen de datos’. Cuando haces esto, para el modelo de regresión múltiple que hemos estado usando como ejemplo en este capítulo, obtienes los resultados que se muestran en Figure 12.27.
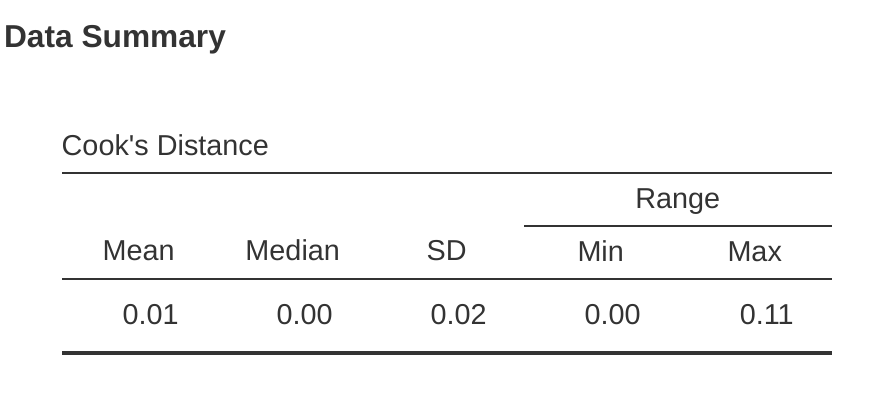
Puedes ver que, en este ejemplo, el valor medio de la distancia de Cook es $ 0.01 $, y el rango es de $ 0.00 $ a $ 0.11 $, por lo que esto se aleja de la regla general mencionada anteriormente de que una distancia de Cook mayor que 1 se considera grande.
Una pregunta obvia para hacer a continuación es, si tienes valores grandes de distancia de Cook, ¿qué debes hacer? Como siempre, no hay una regla estricta y rápida. Probablemente, lo primero que debes hacer es intentar ejecutar la regresión con el valor atípico con la mayor distancia de Cook24 excluido y ver qué sucede con el rendimiento del modelo y con los coeficientes de regresión. Si realmente son sustancialmente diferentes, es hora de comenzar a profundizar en tu conjunto de datos y las notas que sin duda escribías mientras realizabas tu estudio. Trata de averiguar por qué el dato es tan diferente. Si estás convencida de que este punto de datos está distorsionando gravemente sus resultados, entonces podrías considerar excluirlo, pero eso no es ideal a menos que tengas una explicación sólida de por qué este caso en particular es cualitativamente diferente de los demás y, por lo tanto, merece ser manejado por separado.
12.11 Selección del modelo
Un problema bastante importante que persiste es el problema de la “selección del modelo”. Es decir, si tenemos un conjunto de datos que contiene varias variables, ¿cuáles debemos incluir como predictores y cuáles no? En otras palabras, tenemos un problema de selección de variables. En general, la selección de modelos es un asunto complejo, pero se simplifica un poco si nos restringimos al problema de elegir un subconjunto de las variables que deberían incluirse en el modelo. Sin embargo, no voy a tratar de abarcar este tema con mucho detalle. En su lugar, hablaré sobre dos principios generales en los que debes pensar y luego analizaré una herramienta concreta que proporciona jamovi para ayudarte a seleccionar un subconjunto de variables para incluir en tu modelo. En primer lugar, los dos principios:
Es bueno tener una base sustantiva real para tus elecciones. Es decir, en muchas situaciones, tú, la investigadora, tienes buenas razones para seleccionar un pequeño número de posibles modelos de regresión que son de interés teórico. Estos modelos tendrán una interpretación sensata en el contexto de tu campo. Nunca restes importancia a esto. La estadística sirve al proceso científico, no al revés.
En la medida en que tus elecciones se basen en la inferencia estadística, existe un equilibrio entre la simplicidad y la bondad de ajuste. A medida que agregas más predictores al modelo, lo haces más complejo. Cada predictor agrega un nuevo parámetro libre (es decir, un nuevo coeficiente de regresión), y cada nuevo parámetro aumenta la capacidad del modelo para “absorber” variaciones aleatorias. Por lo tanto, la bondad del ajuste (por ejemplo, \(R^2\)) continúa aumentando, a veces de manera trivial o por casualidad, a medida que agregas más predictores sin importar qué. Si deseas que tu modelo pueda generalizarse bien a nuevas observaciones, debes evitar incluir demasiadas variables.
Este último principio a menudo se conoce como la navaja de Ockham y a menudo se resume en la siguiente frase: no multipliques las entidades más allá de lo necesario. En este contexto, significa no introducir un montón de predictores en gran medida irrelevantes solo para aumentar tu R2. Mmm. Sí, el original era mejor.
En cualquier caso, lo que necesitamos es un criterio matemático real que implemente el principio cualitativo detrás de la navaja de Ockham en el contexto de la selección de un modelo de regresión. Pues resulta que hay varias posibilidades. Del que hablaré es del criterio de información de Akaike (Akaike, 1974) simplemente porque está disponible como una opción en jamovi. 25
Cuanto menor sea el valor de AIC, mejor será el rendimiento del modelo. Si ignoramos los detalles de bajo nivel, es bastante obvio lo que hace el AIC. A la izquierda tenemos un término que aumenta a medida que empeoran las predicciones del modelo; a la derecha tenemos un término que aumenta a medida que aumenta la complejidad del modelo. El mejor modelo es el que se ajusta bien a los datos (residuales bajos, lado izquierdo) usando la menor cantidad de predictores posible (K bajo, lado derecho). En resumen, esta es una implementación simple de la navaja de Ockham.
AIC se puede agregar a la tabla de resultados ‘Model Fit Measures’ cuando se hace clic en la casilla de verificación ‘AIC’, y una forma bastante torpe de evaluar diferentes modelos es ver si el valor ‘AIC’ es más bajo si eliminas uno o más de los predictores en el modelo de regresión. Esta es la única forma implementada actualmente en jamovi, pero existen alternativas en otros programas más potentes, como R. Estos métodos alternativos pueden automatizar el proceso de eliminar (o agregar) variables predictoras de forma selectiva para encontrar el mejor AIC. Aunque estos métodos no están implementados en jamovi, los mencionaré brevemente a continuación para que los conozcas.
12.11.1 Eliminación hacia atrás
En la eliminación hacia atrás, comienzas con el modelo de regresión completo, incluidos todos los predictores posibles. Luego, en cada “paso” probamos todas las formas posibles de eliminar una de las variables, y se acepta la que sea mejor (en términos del valor AIC más bajo). Este se convierte en nuestro nuevo modelo de regresión, y luego intentamos todas las eliminaciones posibles del nuevo modelo, eligiendo nuevamente la opción con el AIC más bajo. Este proceso continúa hasta que terminamos con un modelo que tiene un valor de AIC más bajo que cualquiera de los otros modelos posibles que podrías producir eliminando uno de tus predictores.
12.11.2 Selección hacia adelante
Como alternativa, también puedes probar la selección hacia adelante. Esta vez comenzamos con el modelo más pequeño posible como punto de partida y solo consideramos las posibles adiciones al modelo. Sin embargo, hay una complicación. También debes especificar cuál es el modelo más grande posible que estás dispuesta a aceptar.
Aunque la selección hacia atrás y hacia adelante pueden llevar a la misma conclusión, no siempre es así.
12.11.3 Una advertencia
Los métodos automatizados de selección de variables son seductores, especialmente cuando están agrupados en funciones (bastante) simples en poderosos programas estadísticos. Brindan un elemento de objetividad a la selección de tu modelo, y eso es bueno. Desafortunadamente, a veces se usan como excusa para la desconsideración. Ya no tienes que pensar detenidamente qué predictores agregar al modelo y cuál podría ser la base teórica para su inclusión. Todo se soluciona con la magia de AIC. Y si empezamos a lanzar frases como la navaja de Ockham, parece que todo está envuelto en un pequeño y bonito paquete con el que nadie puede discutir.
O, quizás no. En primer lugar, hay muy poco acuerdo sobre lo que cuenta como un criterio de selección de modelo adecuado. Cuando me enseñaron la eliminación hacia atrás como estudiante universitaria, usamos pruebas F para hacerlo, porque ese era el método predeterminado que usaba el software. He descrito el uso de AIC, y dado que este es un texto introductorio, ese es el único método que he descrito, pero el AIC no es la Palabra de los Dioses de la Estadística. Es una aproximación, derivada bajo ciertos supuestos, y se garantiza que funcionará solo para muestras grandes cuando se cumplan esos supuestos. Modifica esos supuestos y obtendrás un criterio diferente, como el BIC, por ejemplo (también disponible en jamovi). Vuelve a adoptar un enfoque diferente y obtendrás el criterio NML. Decide que eres un bayesiano y obtienes una selección de modelo basada en razones de probabilidades posteriores. Luego hay un montón de herramientas específicas de regresión que no he mencionado. Y así sucesivamente. Todos estos métodos diferentes tienen fortalezas y debilidades, y algunos son más fáciles de calcular que otros (AIC es probablemente el más fácil de todos, lo que podría explicar su popularidad). Casi todos producen las mismas respuestas cuando la respuesta es “obvia”, pero hay bastante desacuerdo cuando el problema de selección del modelo se vuelve difícil.
¿Qué significa esto en la práctica? Bueno, podrías pasar varios años aprendiendo por ti misma la teoría de la selección de modelos, aprendiendo todos los entresijos de ella para que finalmente puedas decidir qué es lo que personalmente crees que es lo correcto. Hablando como alguien que realmente hizo eso, no lo recomendaría. Probablemente saldrás aún más confundida que cuando empezaste. Una mejor estrategia es mostrar un poco de sentido común. Si estás mirando los resultados de un procedimiento de selección automatizado hacia atrás o hacia adelante, y el modelo que tiene sentido está cerca de tener el AIC más pequeño pero es derrotado por poco por un modelo que no tiene ningún sentido, entonces confía en tu instinto. La selección de modelos estadísticos es una herramienta inexacta y, como dije al principio, la interpretabilidad es importante.
12.11.4 Comparación de dos modelos de regresión
Una alternativa al uso de procedimientos automatizados de selección de modelos es que el investigador seleccione explícitamente dos o más modelos de regresión para compararlos entre sí. Puedes hacer esto de diferentes maneras, según la pregunta de investigación que estés tratando de responder. Supongamos que queremos saber si la cantidad de sueño que mi hijo durmió o no tiene alguna relación con mi mal humor, más allá de lo que podríamos esperar de la cantidad de sueño que dormí. También queremos asegurarnos de que el día en que tomamos la medida no influya en la relación. Es decir, estamos interesadas en la relación entre baby.sleep y dani.grump, y desde esa perspectiva dani.sleep y day son variables molestas o covariables que queremos controlar. En esta situación, lo que nos gustaría saber es si dani.grump ~ dani.sleep + day + baby .sleep (que llamaré Modelo 2 o M2) es un mejor modelo de regresión para estos datos que dani.grump ~ dani.sleep + day (que llamaré Modelo 1 o M1). Hay dos formas diferentes en que podemos comparar estos dos modelos, una basada en un criterio de selección de modelo como AIC, y la otra basada en una prueba de hipótesis explícita. Primero te mostraré el enfoque basado en AIC porque es más simple y se deriva naturalmente de la discusión en la última sección. Lo primero que debo hacer es ejecutar las dos regresiones, anotar el AIC para cada una y luego seleccionar el modelo con el valor de AIC más pequeño, ya que se considera que es el mejor modelo para estos datos. De hecho, no lo hagas todavía. Sigue leyendo porque en jamovi hay una manera fácil de obtener los valores de AIC para diferentes modelos incluidos en una tabla.26
Un enfoque algo diferente del problema surge del marco de prueba de hipótesis. Supón que tienes dos modelos de regresión, donde uno de ellos (Modelo 1) contiene un subconjunto de los predictores del otro (Modelo 2). Es decir, el Modelo 2 contiene todos los predictores incluidos en el Modelo 1, además de uno o más predictores adicionales. Cuando esto sucede, decimos que el Modelo 1 está anidado dentro del Modelo 2, o posiblemente que el Modelo 1 es un submodelo del Modelo 2. Independientemente de la terminología, lo que esto significa es que podemos pensar en el Modelo 1 como una hipótesis nula y el Modelo 2 como una hipótesis alternativa. Y, de hecho, podemos construir una prueba F para esto de una manera bastante sencilla. 27
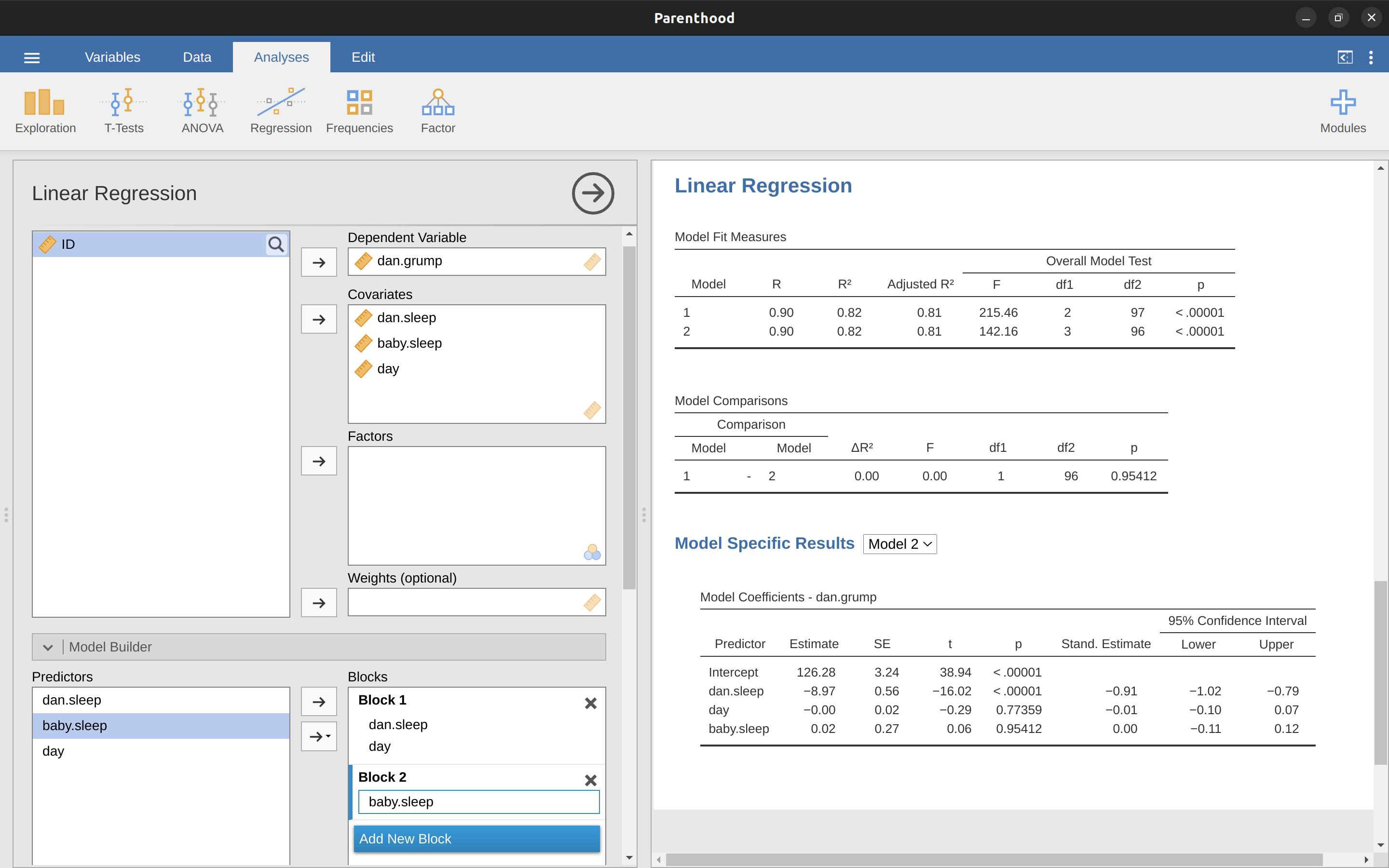
Bien, esa es la prueba de hipótesis que usamos para comparar dos modelos de regresión entre sí. Ahora bien, ¿cómo lo hacemos en jamovi? La respuesta es usar la opción ‘Model Builder’ y especificar los predictores del Modelo 1 dani.sleep y day en el ‘Bloque 1’ y luego agregar el predictor adicional del Modelo 2 (baby.sleep) en el ‘Bloque 2’, como en Figure 12.27. Esto muestra, en la tabla de ‘Comparaciones de modelos’, que para las comparaciones entre el Modelo 1 y el Modelo 2, \(F(1,96) = 0.00\), \(p = 0.954\). Como tenemos p > .05 mantenemos la hipótesis nula (M1). Este enfoque de regresión, en el que agregamos todas nuestras covariables en un modelo nulo, luego agregamos las variables de interés en un modelo alternativo y luego comparamos los dos modelos en un marco de prueba de hipótesis, a menudo se denomina regresión jerárquica .
También podemos usar esta opción de ‘Comparación de modelos’ para construir una tabla que muestra el AIC y BIC para cada modelo, lo que facilita la comparación e identificación de qué modelo tiene el valor más bajo, como en Figure 12.28.
12.12 Resumen
- ¿Quieres saber cómo de fuerte es la relación entre dos variables? Calcular correlaciones
- Dibujo [diagramas de dispersión]
- Ideas básicas sobre ¿Qué es un modelo de regresión lineal? y Estimación de un modelo de regresión lineal
- Regresión lineal múltiple
- Cuantificando el ajuste del modelo de regresión usando \(R^2\).
- Pruebas de hipótesis para modelos de regresión
- En Sobre los coeficientes de regresión hablamos sobre calcular Intervalos de confianza para los coeficientes y Cálculo de coeficientes de regresión estandarizados
- Los Supuestos de regresión y Comprobación del modelo (#sec-Model-checking)
- Regresión [Selección de modelo]
he observado que en jamovi también puedes especificar un tipo de variable ‘ID’, pero para nuestros propósitos no importa cómo especifiquemos la variable ID dado que no lo incluiremos en ningún análisis.↩︎
En realidad, incluso esa tabla es más de lo que me molestaría. En la práctica, la mayoría de las personas eligen una medida de tendencia central y una sola medida de variabilidad.↩︎
la fórmula para el coeficiente de correlación de Pearson se puede escribir de varias maneras diferentes. Creo que la forma más sencilla de escribir la fórmula es dividirla en dos pasos. En primer lugar, introduzcamos la idea de una covarianza. La covarianza entre dos variables \(X\) y \(Y\) es una generalización de la noción de varianza y es una forma matemáticamente simple de describir la relación entre dos variables que no es muy informativa para los humanos \[Cov(X,Y) =\frac{1}{N-1}\sum_{i=1}^N(X_i-\bar{X})(Y_i-\bar{Y})\] Porque estamos multiplicando (es decir, tomando el “producto” de) una cantidad que depende de X por una cantidad que depende de Y y luego promediando \(^a\), puedes pensar en la fórmula para la covarianza como un “producto cruzado promedio” entre \(X\) y \(Y\) . La covarianza tiene la buena propiedad de que, si \(X\) y \(Y\) no están relacionados en absoluto, entonces la covarianza es exactamente cero. Si la relación entre ellos es positiva (en el sentido que se muestra en Figure 12.4, entonces la covarianza también es positiva, y si la relación es negativa, la covarianza también es negativa. En otras palabras, la covarianza captura la idea cualitativa básica de la correlación. Desafortunadamente, la magnitud bruta de la covarianza no es fácil de interpretar, ya que depende de las unidades en las que se expresan \(X\) y \(Y\) y, peor aún, las unidades reales en las que se expresa la covarianza misma son realmente raras. Por ejemplo, si \(X\) se refiere a la variable dani.sleep (unidades: horas) y \(Y\) se refiere a la variable dani.grump (unidades: grumps), entonces las unidades para su covarianza son $horas gruñones \(. Y no tengo ni idea de lo que eso significaría. El coeficiente de correlación de Pearson r soluciona este problema de interpretación al estandarizar la covarianza, más o menos de la misma manera que la puntuación z estandariza una puntuación bruta, al dividir por la desviación estándar. Sin embargo, debido a que tenemos dos variables que contribuyen a la covarianza, la estandarización solo funciona si dividimos entre ambas desviaciones estándar.\)^b$ En otras palabras, la correlación entre \(X\) y \(Y\) se puede escribir de la siguiente manera: \[r_{XY} =\frac{Cov(X,Y)}{\hat{\sigma}_X\hat{\sigma}_Y}\]
—
\(^a\) Tal como vimos con la varianza y la desviación estándar, en la práctica dividimos por \(N - 1\) en lugar de \(N\).
\(^b\) Esta es una simplificación excesiva, pero servirá para nuestros propósitos.↩︎también se escribe a veces como \(y = mx + c\) donde m es el coeficiente de pendiente y \(c\) es el coeficiente de intersección (constante).↩︎
El símbolo \(\epsilon\) es la letra griega epsilon. Es tradicional usar \(\epsilon_i\) o \(e_i\) para indicar un residual.↩︎
O al menos, asumo que no ayuda a la mayoría de las personas. Pero en el caso de que alguien que lea esto sea un verdadero maestro de kung fu de álgebra lineal (y para ser justos, siempre tengo algunas de estas personas en mi clase de introducción a la estadística), te ayudará saber que la solución al problema de estimación resulta ser \(\hat{b} = (X^{'}X)^{-1}X^{'}y\), donde \(\hat{b}\) es un vector que contiene los coeficientes de regresión estimados, \(X\) es la “matriz de diseño” que contiene las variables predictoras (más una columna adicional que contiene todos unos; estrictamente \(X\) es una matriz de los regresores, pero aún no he discutido la distinción), e y es una vector que contiene la variable de resultado. Para todos los demás, esto no es exactamente útil y puede ser francamente aterrador. Sin embargo, dado que bastantes cosas en la regresión lineal se pueden escribir en términos de álgebra lineal, verás un montón de notas al pie como esta en este capítulo. Si puedes seguir las matemáticas en ellas, genial. Si no, ignóralas.↩︎
la fórmula general: la ecuación que di en el texto principal muestra cómo es un modelo de regresión múltiple cuando incluye dos predictores. Entonces, no es sorprendente que si deseas más de dos predictores, todo lo que tienes que hacer es agregar más términos X y más coeficientes b. En otras palabras, si tienes K variables predictoras en el modelo, la ecuación de regresión se verá así \[Y_i=b_0+(\sum_{k=1}^{K}b_k X_{ik})+\epsilon_i\]↩︎
Y por “a veces” me refiero a “casi nunca”. En la práctica, todo el mundo lo llama simplemente “R-cuadrado”.↩︎
el valor \(R^2\) ajustado introduce un ligero cambio en el cálculo, como se muestra a continuación. Para un modelo de regresión con \(K\) predictores, ajustado a un conjunto de datos que contiene \(N\) observaciones, el \(R^2\) ajustado es: \[\text{adj.}R^2=1-(\frac{SS_{ res}}{SS_{tot}} \times \frac{N-1}{NK-1})\]↩︎
formalmente, nuestro “modelo nulo” corresponde al modelo de “regresión” bastante trivial en el que incluimos 0 predictores y solo incluimos el término de intersección \(b_0\): \(H_0: Y_0=b_0+\epsilon_i\) Si nuestro modelo de regresión tiene \(K\) predictores, el “modelo alternativo” se describe utilizando la fórmula habitual para un modelo de regresión múltiple: \[H_1:Y_i=b_0+(\sum_{k=1}^K b_k X_{ik})+\epsilon_i\] ¿Cómo podemos contrastar estas dos hipótesis? El truco es entender que es posible dividir la varianza total \(SStot\) en la suma de la varianza residual SCres y la varianza del modelo de regresión SCmod. Me saltaré los tecnicismos, ya que llegaremos a eso más adelante cuando veamos ANOVA en Chapter 13. Pero ten en cuenta que \(SS_{mod}=SS_{tot}-SS_{res}\) Y podemos convertir las sumas de cuadrados en medias cuadráticas dividiendo por los grados de libertad. \[MS_{mod}=\frac{SS_{mod}}{df_{mod}}\] \[MS_{res}=\frac{SS_{res}}{df_{res}}\] Entonces, ¿cuántos grados de libertad tenemos? Como es de esperar, el gl asociado con el modelo está estrechamente relacionado con la cantidad de predictores que hemos incluido. De hecho, resulta que \(df_mod = K\). Para los residuales, los grados de libertad totales son \(df_res = N - K - 1\). Ahora que tenemos nuestras medias cuadráticas, podemos calcular un estadístico F como este \[F=\frac{MS_{mod}}{MS_{res}}\] y los grados de libertad asociados con esto son $K $ y \(N - K - 1\).↩︎
solo para lectores avanzados. El vector de residuales es \(\epsilon=y - X\hat{b}\). Para K predictores más la intersección, la varianza residual estimada es \(\hat{\sigma}^2 = \frac{\epsilon^{'}\epsilon}{(N - K - 1)}\). La matriz de covarianza estimada de los coeficientes es \(\hat{\sigma}^{2}(X^{'}X)^{-1}\), cuya diagonal principal es \(se(\hat{b})\) , nuestros errores estándar estimados.↩︎
ten en cuenta que, aunque jamovi ha realizado varias pruebas aquí, no ha realizado una corrección de Bonferroni ni nada (consulta Chapter 13). Estas son pruebas t estándar de una muestra con una alternativa bilateral. Si quieres realizar correcciones para varias pruebas, debes hacerlo tú misma.↩︎
Afortunadamente, los intervalos de confianza para los pesos de regresión se pueden construir de la forma habitual \(CI(b)=\hat{b} \pm (t_{crit} \times SE(\hat{b}))\) donde \(se(\hat{b})\) es el error estándar del coeficiente de regresión y t_crit es el valor crítico relevante de la distribución t apropiada. Por ejemplo, si lo que queremos es un intervalo de confianza del 95 %, entonces el valor crítico es el cuantil \(97,5\) de la distribución at con \(N -K -1\) grados de libertad. En otras palabras, este es básicamente el mismo enfoque para calcular los intervalos de confianza que hemos usado en todo momento.↩︎
Estrictamente, estandarizas todos los regresores. Es decir, cada “cosa” que tiene asociado un coeficiente de regresión en el modelo. Para los modelos de regresión de los que he hablado hasta ahora, cada variable predictora se asigna exactamente a un regresor y viceversa. Sin embargo, eso no es cierto en general y veremos algunos ejemplos de esto más adelante en Chapter 14. Pero, por ahora, no necesitamos preocuparnos demasiado por esta distinción.↩︎
Dejando de lado los problemas de interpretación, veamos cómo se calcula. Lo que podrías hacer es estandarizar todas las variables tú misma y luego ejecutar una regresión, pero hay una forma mucho más sencilla de hacerlo. Resulta que el coeficiente \(\beta\) para un predictor \(X\) y un resultado \(Y\) tiene una fórmula muy simple, a saber, \(\beta_X=b_X \times \frac{\sigma_X}{\sigma_Y}\) donde \(\ sigma_X\) es la desviación estándar del predictor, y σY es la desviación estándar de la variable de resultado Y. Esto simplifica mucho las cosas.↩︎
la forma en que los calculamos es dividir el residal ordinario por una estimación de la desviación estándar (poblacional) de estos residuales. Por razones técnicas, la fórmula para esto es \[\epsilon_i^{'}=\frac{\epsilon_i}{\hat{\sigma}\sqrt{1-h_i}}\] donde \(\hat{\sigma}\) en este contexto es la desviación estándar de la población estimada de los residuales ordinarios, y \(h_i\) es el “valor sombrero” de la \(i\)ésima observación. Todavía no te he explicado los valores sombrero, así que esto no tendrá mucho sentido. Por ahora, basta con interpretar los residuales estandarizados como si hubiéramos convertido los residuales ordinarios en puntuaciones z.↩︎
La fórmula para hacer los cálculos esta vez es sutilmente diferente \(\epsilon _i^*=\frac{\epsilon_i}{\hat{\sigma}_{(- i)}\sqrt{1-h_i}}\) Fíjate que nuestra estimación de la desviación estándar aquí se escribe \(\hat{\sigma}_{(-i)}\). Esto corresponde a la estimación de la desviación estándar residual que habría obtenido si hubiera eliminado la i-ésima observación del conjunto de datos. Esto parece una pesadilla de calcular, ya que parece estar diciendo que tienes que ejecutar N nuevos modelos de regresión (incluso un ordenador moderno podría quejarse un poco de eso, especialmente si tienes un gran conjunto de datos). Afortunadamente, esta desviación estándar estimada en realidad viene dada por la siguiente ecuación: \(\hat{\sigma}_{(-i)}= \hat{\sigma}\sqrt{\frac{NK-1-{\epsilon_i^{ '}}^2}{NK-2}}\)↩︎
\(f(x,\lambda)=\frac{x^{\lambda}-1}{\lambda}\) para todos los valores de \(\lambda\) excepto \(\lambda = 0\). Cuando \(\lambda = 0\) simplemente cogemos el logaritmo natural (es decir, ln(\(x\)).↩︎
En jamovi, puedes calcular esta nueva variable usando la fórmula ‘SQRT(ABS(Residuals))’↩︎
Está un poco más allá del alcance de este capítulo hablar sobre cómo tratar las violaciones de la homogeneidad de varianzas, pero te daré una idea rápida de lo que debes tener en cuenta. Lo principal de lo que preocuparse, si se viola la homogeneidad de varianzas, es que las estimaciones del error estándar asociadas con los coeficientes de regresión ya no son completamente fiables, por lo que tus pruebas de \(t\) para los coeficientes no son del todo correctas. Una solución simple al problema es hacer uso de una “matriz de covarianza corregida por heteroscedasticidad” al estimar los errores estándar. Estos a menudo se denominan estimadores sándwich, y se pueden estimar en R (pero no directamente en jamovi).↩︎
La fórmula para el \(k\)-ésimo FIV es: \(VIF_k=\frac{1}{1-R_{-k}^2}\) donde \(R ^2_(-k)\) se refiere al valor R-cuadrado que obtendrías si ejecutaras una regresión utilizando \(X_k\) como variable de resultado y todas las demás variables X como predictores. La idea aquí es que \(R^2_(-k)\) es una muy buena medida de hasta qué punto \(X_k\) se correlaciona con todas las demás variables del modelo. Mejor aún, la raíz cuadrada del FIV es bastante interpretable: te dice cuánto más amplio es el intervalo de confianza para el coeficiente correspondiente \(b_k\), en relación con lo que cabría esperar si todos los predictores fueran buenos y no estuvieran correlacionados entre sí.↩︎
Nuevamente, para los fanáticos del álgebra lineal: la “matriz sombrero” se define como la matriz \(H\) que convierte el vector de valores observados \(y\) en un vector de valores predichos \(\hat{y}\), tal que \(\hat{y} = Hy\). El nombre proviene del hecho de que esta es la matriz que “le pone un sombrero a y”. El valor sombrero de la i-ésima observación es el i-ésimo elemento diagonal de esta matriz (así que técnicamente deberías escribirlo como \(h_{ii}\) en lugar de \(h_i\)). Y así es como se calcula: \(H = X(X^{'}X)^{1}X^{'}\).↩︎
\(D_i=\frac{{\epsilon_i^*}^2}{K+1} \times \frac{h_i}{1-h_i}\) Observa que esto es una multiplicación de algo que mide el valor atípico de la observación (la parte de la izquierda) y algo que mide la influencia de la observación (la parte de la derecha).↩︎
en jamovi, puedes guardar los valores de distancia de Cook en el conjunto de datos y luego dibujar un diagrama de caja de los valores de distancia de Cook para identificar los valores atípicos específicos. O podrías usar un programa de regresión más poderoso, como el paquete ‘car’ en R, que tiene más opciones para el análisis de diagnóstico de regresión avanzado.↩︎
en el contexto de un modelo de regresión lineal (¡e ignorando los términos que no dependen del modelo de ninguna manera!), el AIC para un modelo que tiene un predictor con K variables más una intersección es \(AIC=\frac{SS_{res}}{\hat{\sigma}^2}+2K\)↩︎
Mientras estoy en este tema, debo señalar que la evidencia empírica sugiere que BIC es un mejor criterio que AIC. En la mayoría de los estudios de simulación que he visto, BIC trabaja mucho mejor al seleccionar el modelo correcto.↩︎
podemos ajustar ambos modelos a los datos y obtener una suma de cuadrados residual para ambos modelos. Los denotaré como \(SS_{res}^{(1)}\) y \(SS_{res}^{(2)}\) respectivamente. El superíndice aquí solo indica de qué modelo estamos hablando. Entonces nuestro estadístico F es \[F= \frac {\frac {SS _{res}^{(1)} - SS_{res}^{(2)}} {k}} {\frac{SS_{res} ^2} {Np-1} }\] donde \(N\) es el número de observaciones, \(p\) es el número de predictores en el modelo completo (sin incluir la intersección) y \(k\) es la diferencia en el número de parámetros entre los dos modelos. \(^d\) Los grados de libertad aquí son \(k\) y \(N -p-1\). Ten en cuenta que a menudo es más conveniente pensar en la diferencia entre esos dos valores de SC como una suma de cuadrados en sí. Eso es \[SS_\Delta=SS_{res}^{(1)}-SS_{res}^{(2)}\] La razón por la que esto es útil es que podemos expresar \(SS_\Delta\) como una medida de hasta qué punto los dos modelos hacen diferentes predicciones sobre la variable de resultado. Específicamente, \[SS_\Delta=\sum_i{(\hat{y}_i^{(2)}-\hat{y}_i^{(1)})^2}\] donde \(\hat{y} _{i^{(1)}}\) es el valor previsto para \(y_i\) según el modelo \(M_1\) y \(\hat{y}_{i^{(2)}}\) es el valor previsto para $y_i $ según modelo \(M_2\).
—
\(^d\) Vale la pena señalar de paso que este mismo estadístico F se puede usar para probar una gama mucho más amplia de hipótesis que las que estoy mencionando aquí. Muy brevemente, observa que el modelo anidado M1 corresponde al modelo completo M2 cuando restringimos algunos de los coeficientes de regresión a cero. A veces es útil construir submodelos colocando otros tipos de restricciones en los coeficientes de regresión. Por ejemplo, quizás dos coeficientes diferentes tengan que sumar cero. También puedes construir pruebas de hipótesis para ese tipo de restricciones, pero es un poco más complicado y la distribución muestral de F puede terminar siendo algo conocido como distribución F no central, que está mucho más allá del alcance de este libro. Todo lo que quiero hacer es alertarte de esta posibilidad.↩︎