| levels | Counts | \(\%\) of Total | Cumulative \(\%\) |
|---|---|---|---|
| makka-pakka | 4 | 40\(\%\) | 40\(\%\) |
| tombliboo | 2 | 20\(\%\) | 60\(\%\) |
| upsy-daisy | 4 | 40\(\%\) | 100\(\%\) |
6 Cuestiones prácticas
El jardín de la vida nunca parece limitarse a las parcelas que los filósofos han trazado para su conveniencia. Tal vez algunos tractores más bastarían.
– Roger Zelazny1
Este es un capítulo un tanto extraño, incluso para mis estándares. Mi objetivo en este capítulo es hablar sobre las realidades de trabajar con datos un poco más honestamente de lo que verás en cualquier otra parte del libro. El problema con los conjuntos de datos del mundo real es que están desordenados. Muy a menudo, el archivo de datos con el que comienzas no tiene las variables almacenadas en el formato correcto para el análisis que quieres realizar. A veces puede puede que falten muchos valores en el conjunto de datos. A veces, solo quieres analizar un subconjunto de los datos. Etcétera. En otras palabras, hay un montón de manipulación de datos que necesitas hacer solo para obtener las variables en el formato que necesitas. El propósito de este capítulo es proporcionar una introducción básica a estos temas prácticos. Aunque el capítulo está motivado por los tipos de problemas prácticos que surgen cuando se manipulan datos reales, seguiré con la práctica que he adoptado durante la mayor parte del libro y me basaré en conjuntos de datos muy pequeños que ilustran el problema subyacente. Como este capítulo es esencialmente una colección de técnicas y no cuenta una sola historia coherente, puede ser útil empezar con una lista de temas:
- Tabulación y tabulación cruzada de datos
- Expresiones lógicas en jamovi
- Transformar y recodificar una variable
- Otras funciones y operaciones matemáticas
- Extracción de un subconjunto de datos
Como puedes ver, la lista de temas que cubre el capítulo es bastante amplia y hay mucho contenido. Aunque este es uno de los capítulos más largos y difíciles del libro, en realidad solo estoy arañando la superficie de varios temas bastante diferentes e importantes. Mi consejo, como siempre, es que leas el capítulo una vez e intentes seguirlo todo lo que puedas. No te preocupe demasiado si no puedes entenderlo todo de una vez, especialmente las últimas secciones. El resto del libro depende muy poco de este capítulo, así que puedes conformarte con entender lo básico. Sin embargo, lo más probable es que más adelante tengas que volver a este capítulo para entender algunos de los conceptos a los que me refiero aquí.
6.1 Tabulación y tabulación cruzada de datos
Una tarea muy común al analizar datos es la construcción de tablas de frecuencia, o tabulación cruzada de una variable contra otra. Esto se puede conseguir en jamovi y te mostraré cómo en esta sección.
6.1.1 Creación de tablas para variables individuales
Comencemos con un ejemplo simple. Como padre de un niño pequeño, naturalmente paso mucho tiempo viendo programas de televisión como In the Night Garden. En el archivo nightgarden.csv, transcribí una breve sección del diálogo. El archivo contiene dos variables de interés, locutor y enunciado. Abre este conjunto de datos en jamovi y echa un vistazo a los datos en la vista de ‘hoja de cálculo’. Verás que los datos tienen este aspecto:
variable ‘locutor’: upsy-daisy upsy-daisy upsy-daisy upsy-daisy tombliboo tombliboo makka-pakka makka-pakka makka-pakka makka-pakka variable de ‘pronunciación’: pip pip onk onk ee oo pip pip onk onk
¡Mirando esto queda muy claro lo que le pasó a mi cordura! Con estos como mis datos, una tarea que podría necesitar hacer es construir un recuento de frecuencia de la cantidad de palabras que habla cada personaje durante el programa. La pantalla ‘Descriptivas’ de jamovi tiene una casilla de verificación llamada ‘Tablas de frecuencia’ que hace exactamente esto, consulta Table 6.1.
El resultado aquí nos dice en la primera línea que lo que estamos viendo es una tabulación de la variable locutor. En la columna ‘Niveles’ enumera los diferentes locutores que existen en los datos, y en la columna ‘Recuentos’ te dice cuántas veces aparece ese locutor en los datos. En otras palabras, es una tabla de frecuencias.
En jamovi, la casilla de verificación ‘Tablas de frecuencia’ solo producirá una tabla para variables individuales. Para una tabla de dos variables, por ejemplo, combinar locutor y enunciado para que podamos ver cuántas veces cada locutor dijo un enunciado en particular, necesitamos una tabulación cruzada o una tabla de contingencia. En jamovi, puedes hacer esto seleccionando el análisis ‘Frecuencias’ - ‘Tablas de contingencia’ - ‘Muestras independientes’ y moviendo la variable del locutor al cuadro ‘Filas’ y la variable de expresiones al cuadro ‘Columnas’. Entonces deberías tener una tabla de contingencia como la que se muestra en Figure 6.1.

No te preocupes por la tabla “\(\chi^2\) Tests” que se genera. Veremos esto más adelante en Chapter 10. Al interpretar la tabla de contingencia recuerda que estos son recuentos, por lo que el hecho de que la primera fila y la segunda columna de números correspondan a un valor de 2 indica que Makka-Pakka (fila 1) dice “onk” (columna 2) dos veces en este conjunto de datos.
6.1.2 Añadir porcentajes a una tabla de contingencia
La tabla de contingencia que se muestra en Figure 6.1 muestra una tabla de frecuencias brutas. Es decir, un recuento del número total de casos para diferentes combinaciones de niveles de las variables especificadas. Sin embargo, a menudo quieres que tus datos se organicen en términos de porcentajes y recuentos. Puedes encontrar las casillas de verificación para diferentes porcentajes en la opción ‘Celdas’ en la ventana ‘Tablas de contingencia’. Primero, haz clic en la casilla de verificación ‘Fila’ y la tabla de contingencia en la ventana de resultados cambiará a la de Figure 6.2.
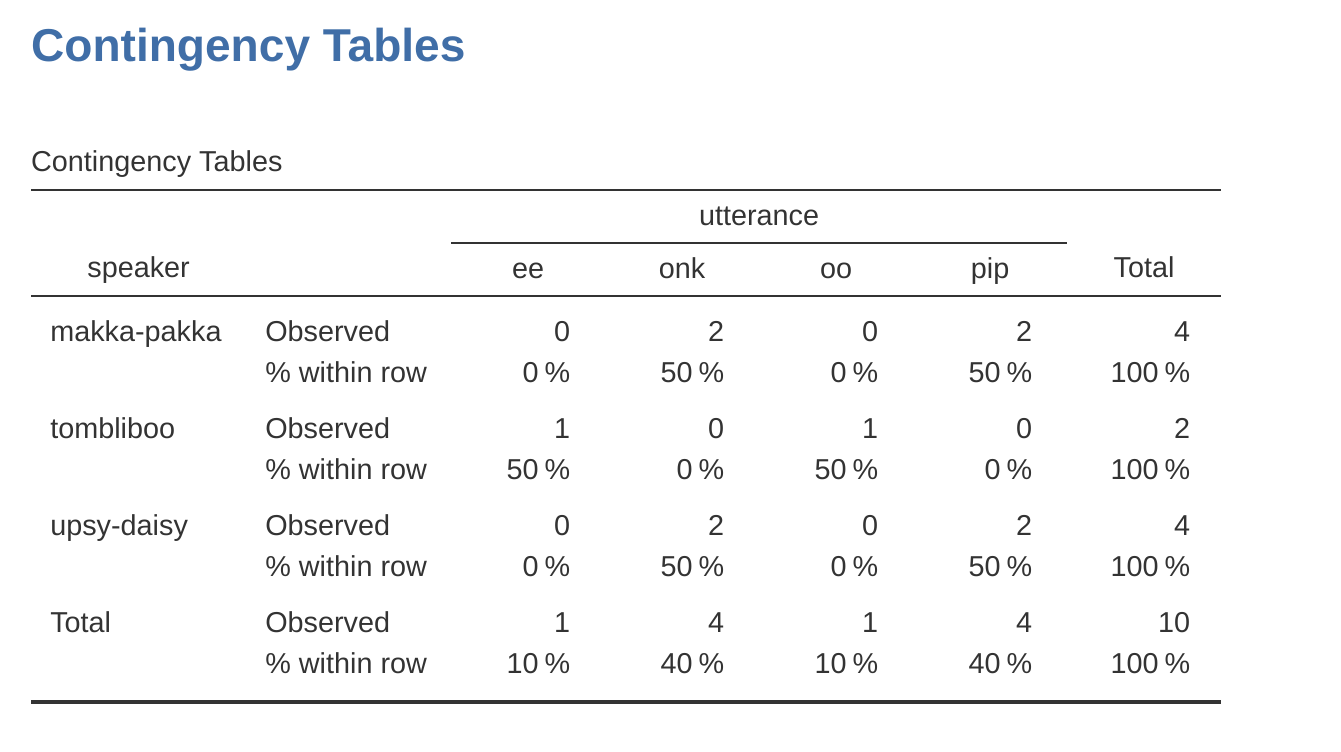
Lo que estamos viendo aquí es el porcentaje de expresiones hechas por cada personaje. En otras palabras, el 50% de las declaraciones de Makka-Pakka son “pip” y el otro 50% son “onk”. Comparemos esto con la tabla que obtenemos cuando calculamos los porcentajes de columna (desmarca ‘Fila’ y marca ‘Columna’ en la ventana de opciones de Celdas), ver Figure 6.3. En esta versión, lo que vemos es el porcentaje de caracteres asociados con cada enunciado. Por ejemplo, cada vez que se hace la expresión “ee” (en este conjunto de datos), el 100 % de las veces es un Tombliboo quien lo dice.

6.2 Expresiones lógicas en jamovi
Un concepto clave en el que se basan muchas transformaciones de datos en jamovi es la idea de un valor lógico. Un valor lógico es una afirmación sobre si algo es verdadero o falso. Esto se implementa en jamovi de una manera bastante sencilla. Hay dos valores lógicos, a saber, VERDADERO y FALSO. A pesar de la simplicidad, los valores lógicos son muy útiles. Veamos cómo funcionan.
6.2.1 Evaluar verdades matemáticas
En el libro clásico de George Orwell de 1984, uno de los lemas utilizados por el Partido totalitario era “dos más dos es igual a cinco”. La idea es que la dominación política de la libertad humana se completa cuando es posible subvertir incluso la más básica de las verdades. Es un pensamiento aterrador, especialmente cuando el protagonista Winston Smith finalmente se derrumba bajo la tortura y acepta la propuesta. “El hombre es infinitamente maleable”, dice el libro. Estoy bastante segura de que esto no es cierto para los humanos2 y definitivamente no es cierto para jamovi. jamovi no es infinitamente maleable, tiene opiniones bastante firmes sobre el tema de lo que es y no es cierto, al menos en lo que respecta a las matemáticas básicas. Si le pido que calcule \(2 + 2\)3, siempre da la misma respuesta, ¡y no es un 5!
Por supuesto, hasta ahora jamovi solo está haciendo los cálculos. No le he pedido que afirme explícitamente que \(2 + 2 = 4\) es una afirmación verdadera. Si quiero que jamovi haga un juicio explícito, puedo usar un comando como este: \(2 + 2 == 4\)
Lo que he hecho aquí es usar el operador de igualdad, \(==\), para obligar a jamovi a hacer un juicio de “verdadero o falso”.4 el eslogan del Partido, así que escribe esto en el cuadro Calcular nueva variable ‘fórmula’:
\[2 + 2 == 5\]
¿Y qué obtienes? Debería ser un conjunto completo de valores ‘falsos’ en la columna de la hoja de cálculo para tu variable recién calculada. ¡Yupi! ¡Libertad y ponis para todos! O algo así. De todos modos, valió la pena echar un vistazo a lo que sucede si intentas obligar a jamovi a creer que dos más dos son cinco haciendo una afirmación como \(2 + 2 = 5\). Sé que si hago esto en otro programa, digamos R, nos da un mensaje de error. Pero espera, si haces esto en jamovi obtienes un conjunto completo de valores ‘falsos’. ¿Entonces qué está pasando? Bueno, parece que jamovi está siendo bastante inteligente y se da cuenta de que está probando si es VERDADERO o FALSO que \(2 + 2 = 5\), independientemente de si usas el operador de igualdad correcto, \(==\), o el signo igual “\(=\)”.
6.2.2 Operaciones lógicas
Ya hemos visto cómo funcionan las operaciones lógicas. Pero hasta ahora solo hemos visto el ejemplo más sencillo posible. Probablemente no te sorprenderá descubrir que podemos combinar operaciones lógicas con otras operaciones y funciones de una manera más complicada, como esta: \(3 \times 3 + 4 \times 4 == 5 \times 5\) o esto \(SQRT( 25) == 5\)
No solo eso, sino que, como ilustra Table 6.2, existen otros operadores lógicos que puedes usar y que corresponden a algunos conceptos matemáticos básicos. Esperamos que todos estos se expliquen por sí mismos. Por ejemplo, el operador menor que < verifica si el número de la izquierda es menor que el número de la derecha. Si es menor, entonces jamovi devuelve una respuesta de VERDADERO, pero si los dos números son iguales, o si el de la derecha es mayor, entonces jamovi devuelve una respuesta de FALSO.
Por el contrario, el operador menor que o igual a \(<=\) hará exactamente lo que dice. Devuelve un valor de VERDADERO si el número del lado izquierdo es menor o igual que el número del lado derecho. En este punto, espero que sea bastante obvio lo que hacen el operador mayor que \(>\) y el operador mayor que o igual a \(>=\).
El siguiente en la lista de operadores lógicos es el operador distinto de != que, como todos los demás, hace lo que dice que hace. Devuelve un valor de VERDADERO cuando las cosas en cualquier lado no son idénticas entre sí. Por lo tanto, dado que \(2 + 2\) no es igual a \(5\), obtendríamos ‘verdadero’ como el valor de nuestra variable recién calculada. Pruébalo y verás:
\[2 + 2 \text{ != } 5\]
Aún no hemos terminado. Hay tres operaciones lógicas más que vale la pena conocer, enumeradas en Table 6.3. Estos son el operador no !, el operador y and, y el operador o or. Al igual que los otros operadores lógicos, su comportamiento es más o menos el que cabría dados sus nombres. Por ejemplo, si te pido que evalúes la afirmación de que “o bien \(2 + 2 = 4\) o \(2 + 2 = 5\)”, dirías que es verdad. Dado que es una declaración de “o esto o lo otro”, lo que necesitamos es que una de las dos partes sea verdadera. Eso es lo que hace el operador or:5
| operation | operator | example input | answer |
|---|---|---|---|
| less than | 2 | TRUE | |
| less than or equal to | < | 2 < = 2 | TRUE |
| greater than | > | 2 > 3 | FALSE |
| greater than or equal to | > = | 2 > = 2 | TRUE |
| equal to | = = | 2 = = 3 | FALSE |
| not equal to | != | 2 != 3 | TRUE |
| operation | operator | example input | answer |
|---|---|---|---|
| not | NOT | NOT(1==1) | FALSE |
| or | or | (1==1) or (2==3) | TRUE |
| and | and | (1==1) and (2==3) | FALSE |
\[(2+2 == 4) \text{ o } (2+2 == 5)\]
Por otro lado, si te pido que evalúes la afirmación de que “ambos \(2 + 2 = 4\) y \(2 + 2 = 5\)”, dirías que es falso. Dado que se trata de una afirmación y necesitamos que ambas partes sean verdaderas. Y eso es lo que hace el operador and:
\[(2+2 == 4) \text{ y } (2+2 == 5)\]
Finalmente, está el operador not, que es simple pero molesto de describir en inglés. Si te pido que evalúes mi afirmación de que “no es cierto que \(2 + 2 = 5\)”, entonces dirías que mi afirmación es verdadera, porque en realidad mi afirmación es que “\(2 + 2 = 5\) es falso”. Y tengo razón. Si escribimos esto en jamovi usamos esto:
\[NO(2+2 == 5)\]
En otras palabras, dado que \(2+2 == 5\) es una afirmación FALSA, debe darse el caso de que \(NO(2+2 == 5)\) sea VERDADERA. Esencialmente, lo que realmente hemos hecho es afirmar que “no falso” es lo mismo que “verdadero”. Obviamente, esto no es del todo correcto en la vida real. Pero jamovi vive en un mundo mucho más blanco o negro. Para jamovi todo es verdadero o falso. No se permiten matices de gris.
Por supuesto, en nuestro ejemplo de \(2 + 2 = 5\), realmente no necesitábamos usar el operador “no” \(NOT\) y el operador “igual a” \(==\) como dos operadores separados. Podríamos haber usado el operador “no es igual a” \(!=\) así:
\[2+2 \text{ != } 5\]
6.2.3 Aplicando operaciones lógicas al texto
También quiero señalar brevemente que puedes aplicar estos operadores lógicos tanto a texto como a datos lógicos. Pero hay que tener un poco más de cuidado a la hora de entendercómo jamovi interpreta las diferentes operaciones. En esta sección hablaré de cómo se aplica el operador igual a \(==\) al texto, ya que es el más importante. Obviamente, el operador no igual a != da exactamente las respuestas opuestas a \(==\), por lo que implícitamente también estoy hablando de eso, pero no daré comandos específicos que muestren el uso de \(!=\).
Bien, veamos cómo funciona. En cierto sentido, es muy sencillo. Por ejemplo, puedo preguntarle a jamovi si la palabra “gato” es lo mismo que la palabra “perro”, así:
“gato” \(==\) “perro” Esto es bastante obvio, y es bueno saber que incluso jamovi puede darse cuenta. De manera similar, jamovi reconoce que un “gato” es un “gato”: “gato” \(==\) “gato” Nuevamente, eso es exactamente lo que esperaríamos. Sin embargo, lo que debes tener en cuenta es que jamovi no es nada tolerante en lo que respecta a la gramática y el espaciado. Si dos cadenas difieren de alguna manera, jamovi dirá que no son iguales entre sí, como con lo siguiente: ” cat” \(==\) “cat” “cat” \(==\) “CAT” “cat” \(==\) “ca t”
También puedes usar otros operadores lógicos. Por ejemplo, jamovi también te permite usar los operadores > y < para determinar cuál de las dos ‘cadenas’ de texto viene primero, alfabéticamente hablando. Más o menos. En realidad, es un poco más complicado que eso, pero empecemos con un ejemplo sencillo:
“gato” \(<\) “perro”
En jamovi, este ejemplo se evalúa como ‘verdadero’. Esto se debe a que “gato” viene antes que “perro” en orden alfabético, por lo que jamovi considera que la afirmación es verdadera. Sin embargo, si le pedimos a jamovi que nos diga si “gato” viene antes que “zorro”, evaluará la expresión como falsa. Hasta aquí todo bien. Pero los datos de texto son un poco más complicados de lo que sugiere el diccionario. ¿Qué pasa con “gato” y “GATO”? ¿Cuál de estos viene primero? Pruébalo y descúbrelo:
“GATO” \(<\) “gato”
De hecho, esto se evalúa como ‘verdadero’. En otras palabras, jamovi asume que las letras mayúsculas van antes que las minúsculas. Me parece bien. Es probable que no te sorprenda. Lo que podría sorprenderte es que jamovi asume que todas las letras mayúsculas van antes que las minúsculas. Es decir, mientras que “ardilla” \(<\) “zorro” es una afirmación verdadera, y el equivalente en mayúsculas “ARDILLA” \(<\) “ZORRO” también es cierto, no es cierto decir que “ardilla” \(<\) “ZORRO” “, como ilustra el siguiente extracto. Prueba esto:
“ardilla” \(<\) “ZORRO”
Esto se evalúa como ‘falso’, y puede parecer un poco contraintuitivo. Con eso en mente, puede ser útil echar un vistazo rápido a Table 6.4 que enumera varios caracteres de texto en el orden en que jamovi los procesa.
| \( \text{!} \) | \( \text{"} \) | \( \# \) | \( \text{\$} \) | \( \% \) | \( \& \) | \( \text{'} \) | \( \text{(} \) |
|---|---|---|---|---|---|---|---|
| \( \text{)} \) | \( \text{*} \) | \( \text{+} \) | \( \text{,} \) | \( \text{-} \) | \( \text{.} \) | \( \text{/} \) | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | \( \text{:} \) | \( \text{;} \) | < | \( \text{=} \) | > | \( \text{?} \) | \( \text{@} \) |
| A | B | C | D | E | F | G | H |
| I | J | K | L | M | N | O | P |
| Q | R | S | T | U | V | W | X |
| Y | Z | \( \text{[} \) | \( \backslash \) | \( \text{]} \) | \( \hat{} \) | \( \_ \) | \( \text{`} \) |
| a | b | c | d | e | g | h | i |
| j | k | l | m | n | o | p | q |
| r | s | t | u | v | w | x | y |
| z | \(\text{\{}\) | \(\text{|}\) | \(\text{\}}\) |
6.3 Transformar y recodificar una variable
En el análisis de datos del mundo real, no es infrecuente encontrarse con que una de las variables no es exactamente equivalente a la variable que realmente quieres. Por ejemplo, a menudo es conveniente tomar una variable de valor continuo (p. ej., la edad) y dividirla en un número más pequeño de categorías (p. ej., más joven, mediana, mayor). En otras ocasiones, es posible que necesites convertir una variable numérica en una variable numérica diferente (p. ej., puede que quieras analizar el valor absoluto de la variable original). En esta sección, describiré algunas formas clave de hacer estas cosas en jamovi.
6.3.1 Crear una variable transformada
El primer truco a discutir es la idea de transformar una variable. Literalmente, cualquier cosa que hagas a una variable es una transformación, pero en la práctica lo que generalmente significa es que aplicas una función matemática relativamente simple a la variable original para crear una nueva variable que (a) describa mejor lo que realmente te interesa, o (b) esté más de acuerdo con los supuestos de las pruebas estadísticas que quieres hacer. Como hasta ahora no he hablado de las pruebas estadísticas ni de sus supuestos, te mostraré un ejemplo basado en el primer caso.
Supongamos que he realizado un breve estudio en el que hago una sola pregunta a 10 personas:
En una escala de 1 (totalmente en desacuerdo) a 7 (totalmente de acuerdo), ¿en qué medida está de acuerdo con la afirmación de que “los dinosaurios son increíbles”?
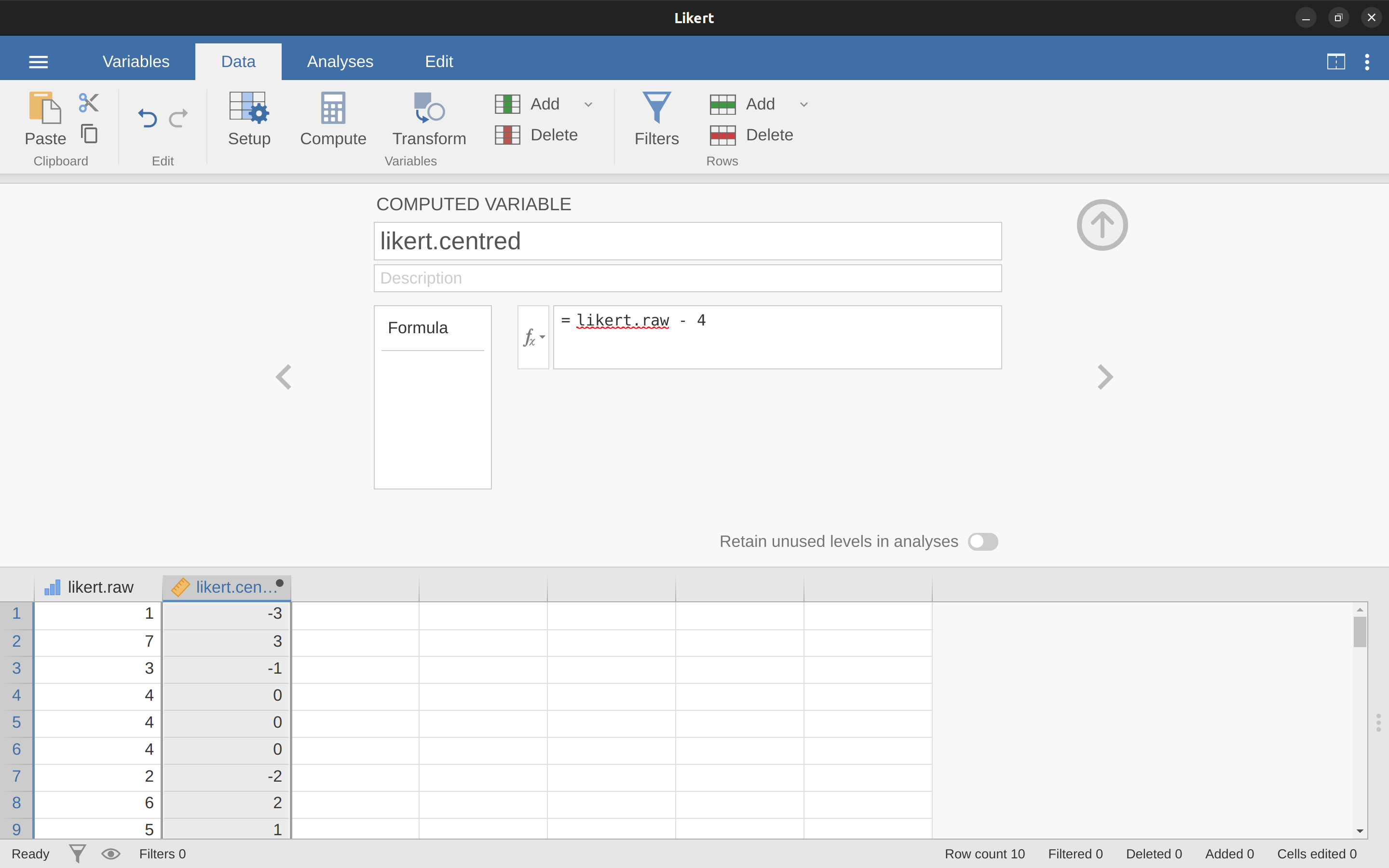
Ahora vamos a cargar y ver los datos. El archivo de datos likert.omv contiene una única variable con las respuestas brutas en escala Likert para estas 10 personas. Sin embargo, si se piensa en ello, esta no es la mejor manera de representar estas respuestas. Debido a la forma bastante simétrica en que configuramos la escala de respuesta, en cierto sentido el punto medio de la escala debería haber sido codificado como 0 (sin opinión), y los dos puntos finales deberían ser `3 (totalmente de acuerdo) y ´ 3 (totalmente en desacuerdo). Al recodificar los datos de esta manera, refleja un poco más cómo pensamos realmente sobre las respuestas. La recodificación aquí es bastante sencilla, simplemente restamos 4 de las puntuaciones brutas. En jamovi puedes hacer esto calculando una nueva variable: haz clic en el botón ‘Datos’ - ‘Calcular’ y verás que se ha agregado una nueva variable a la hoja de cálculo. Llamemos a esta nueva variable likert.centred (tecléalo) y luego añade lo siguiente en el cuadro de fórmulas, como en Figure 6.4: ‘likert.raw - 4’
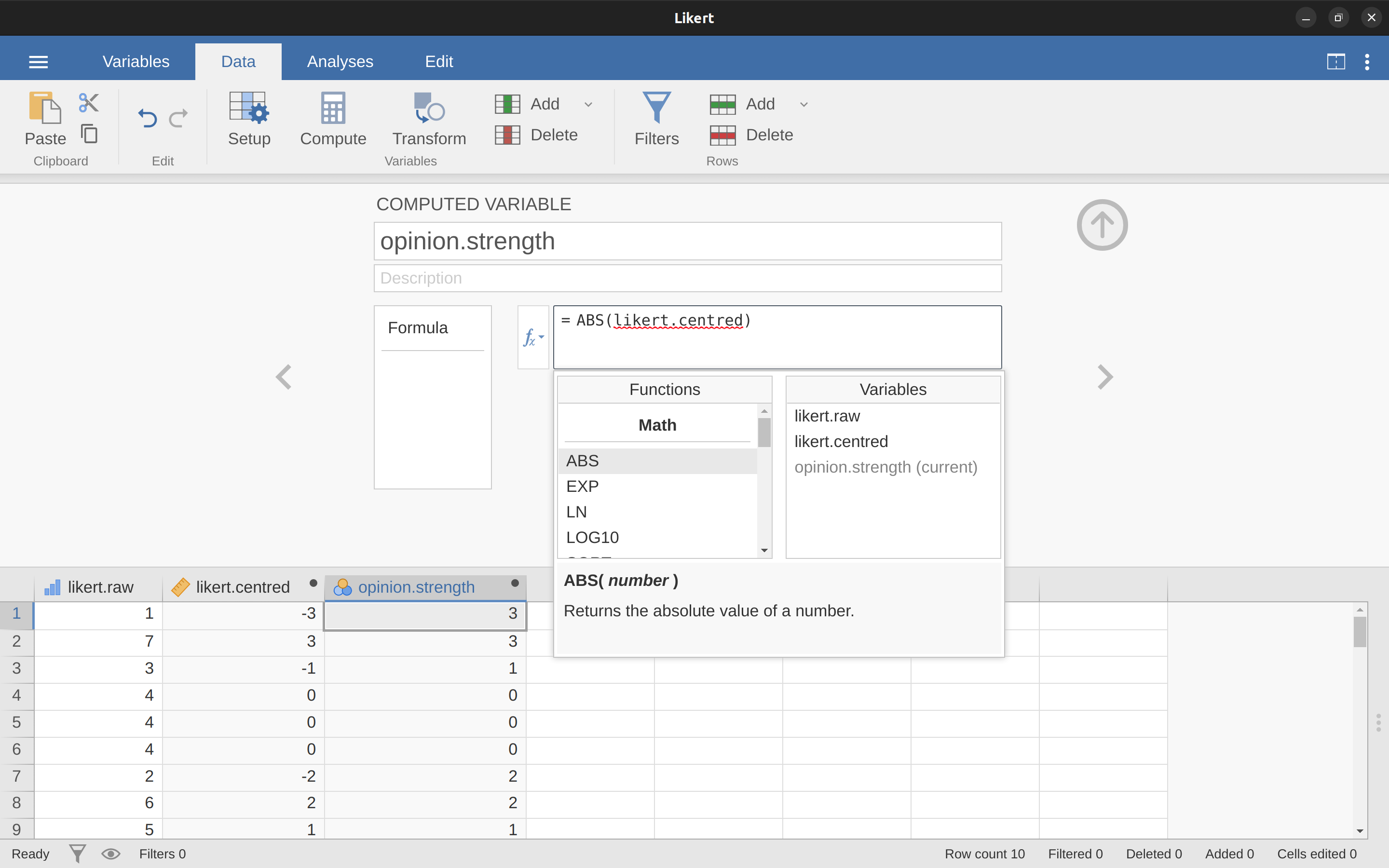
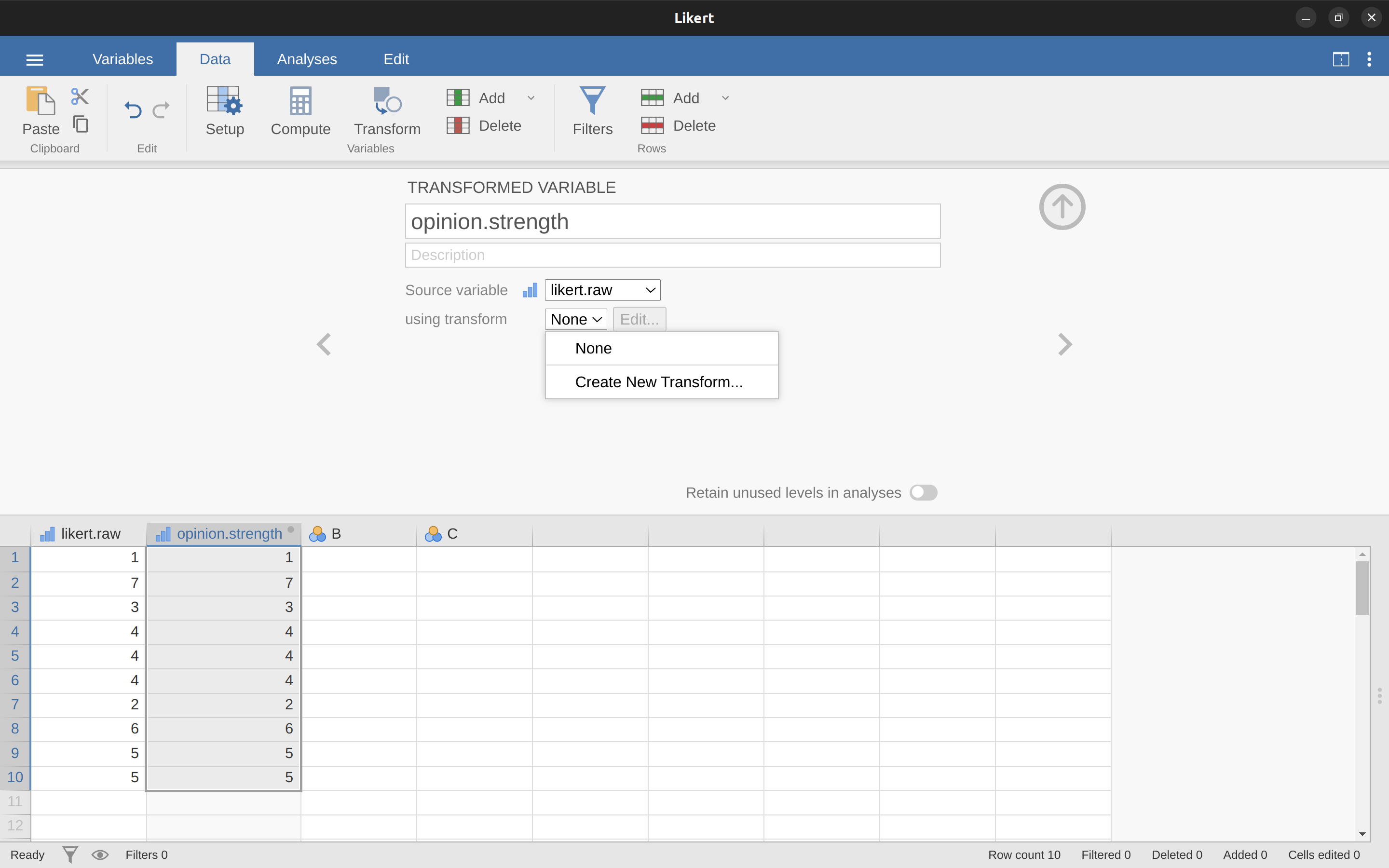
Una de las razones por las que puede ser útil tener los datos en este formato es que hay muchas situaciones en las que se puede preferir analizar la fuerza de la opinión por separado de la dirección de la opinión. Podemos hacer dos transformaciones diferentes en esta variable Likert centrada para distinguir entre estos dos conceptos diferentes. Primero, para calcular la variable opinion.strength (fuerza de la opinión) coge el valor absoluto de los datos centrados (usando la función ‘ABS’).6 En jamovi se crea una nueva variable utilizando el botón ‘Calcular’. Llama a la variable opinion.strength y esta vez haz clic en el botón fx situado al lado de la casilla ‘Fórmula’. Esto muestra las diferentes ‘Funciones’ y ‘Variables’ que puedes añadir a la casilla ‘Fórmula’, así que haz doble clic en ‘ABS’ y luego doble clic en “likert.centred” y verás que la casilla ‘Fórmula’ se rellena con ABS(likert.centred) y se ha creado una nueva variable en la vista de hoja de cálculo, como en Figure 6.5.
En segundo lugar, para calcular una variable que contiene solo la dirección de la opinión e ignora la fuerza, queremos calcular el ‘signo’ de la variable. En jamovi podemos usar la función IF para hacerlo. Crea otra nueva variable con el botón ‘Calcular’, llámala opinion.sign, y luego escribe lo siguiente en el cuadro de función:
IF(likert.centred \(==\) 0, 0, likert.centred / opinion.strength) Cuando termines, verás que todos los números negativos de la variable likert.centred se convierten en -1, todos los números positivos se convierten en 1 y cero se queda como 0, así:
-1 1 -1 0 0 0 -1 1 1 1
Analicemos qué está haciendo este comando ‘IF’. En jamovi hay tres partes en una declaración ‘IF’, escrita como ‘IF (expression, value, else)’. La primera parte, ‘expression’, puede ser un enunciado lógico o matemático. En nuestro ejemplo, hemos especificado ‘likert.centred \(==\) 0’, que es VERDADERO para valores donde likert.centred es cero. La siguiente parte, ‘value’, es el nuevo valor donde la expresión en la primera parte es VERDADERA. En nuestro ejemplo, hemos dicho que para todos aquellos valores donde likert.centred es cero, mantenlos en cero. En la siguiente parte, ‘else’, podemos incluir un enunciado lógico o matemático que se usará si la parte uno se evalúa como FALSO, es decir, donde likert.centred no es cero. En nuestro ejemplo hemos dividido likert.centred por opinion.strength para dar ‘-1’ o ‘+1’ dependiendo del signo del valor original en likert.centred.7
Y ya está. Ahora tenemos tres nuevas variables brillantes, todas las cuales son transformaciones útiles de los datos originales de likert.raw.
6.3.2 Descomponer una variable en un número menor de niveles discretos o categorías
Una tarea práctica que surge con bastante frecuencia es el problema de descomponer una variable en un número menor de niveles o categorías discretos. Por ejemplo, supongamos que estoy interesada en observar la distribución por edades de las personas en una reunión social:
60,58,24,26,34,42,31,30,33,2,9
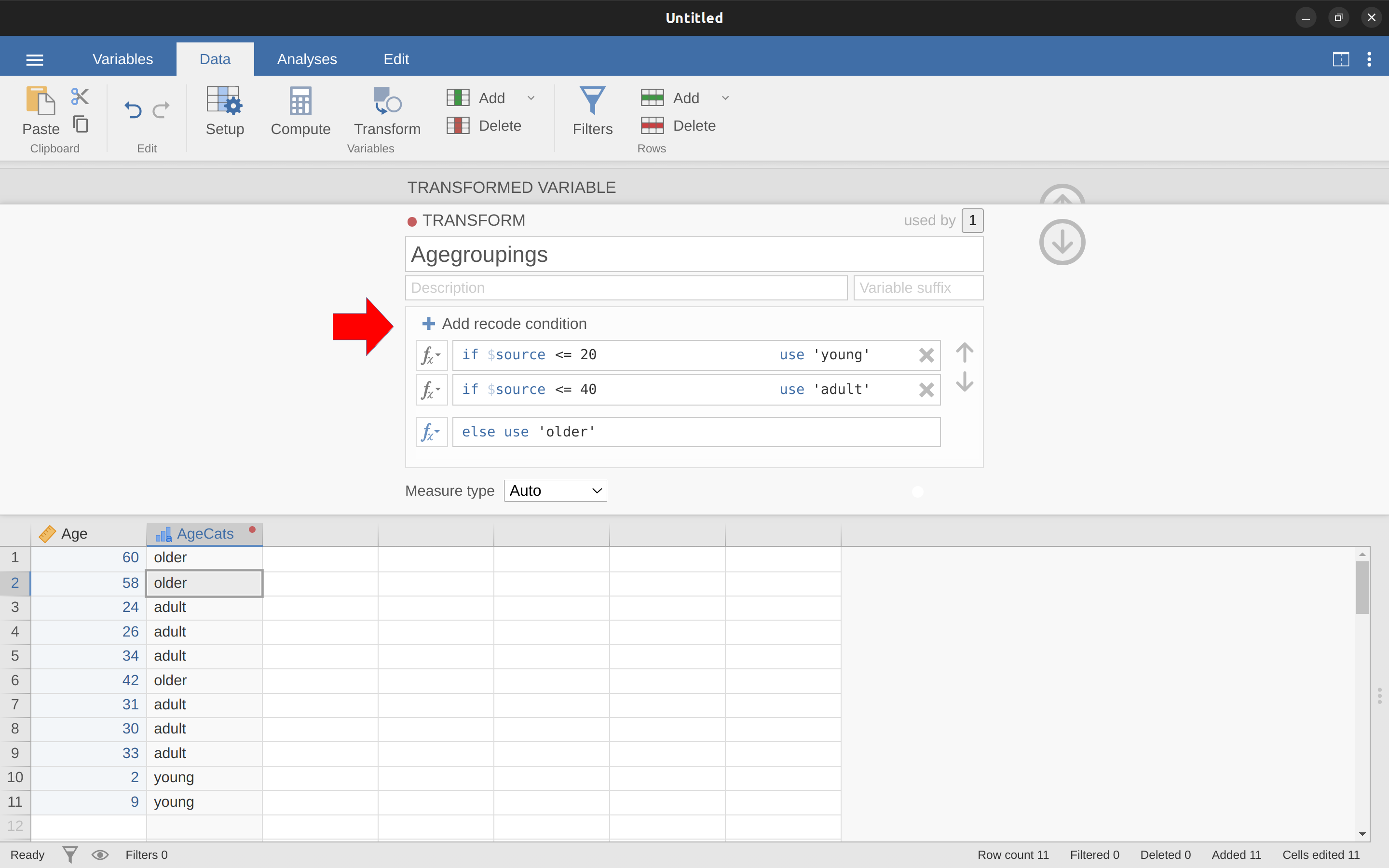
En algunas situaciones, puede ser muy útil agruparlos en un número reducido de categorías. Por ejemplo, podríamos agrupar los datos en tres grandes categorías: jóvenes (0-20), adultos (21-40) y mayores (41-60). Se trata de una clasificación bastante tosca, y las etiquetas que he adjuntado solo tienen sentido en el contexto de este conjunto de datos (por ejemplo, visto de manera más general, una persona de 42 años no se consideraría “mayor”). Podemos dividir esta variable con bastante facilidad usando la función jamovi ‘IF’ que ya hemos usado. Esta vez tenemos que especificar declaraciones ‘IR’ anidadas, lo que significa simplemente que SI la primera expresión lógica es VERDADERA, inserte un primer valor, pero SI una segunda expresión lógica es VERDADERA, inserte un segundo valor, pero SI una tercera expresión lógica es VERDADERA , luego inserte un tercer valor. Esto se puede escribir como:
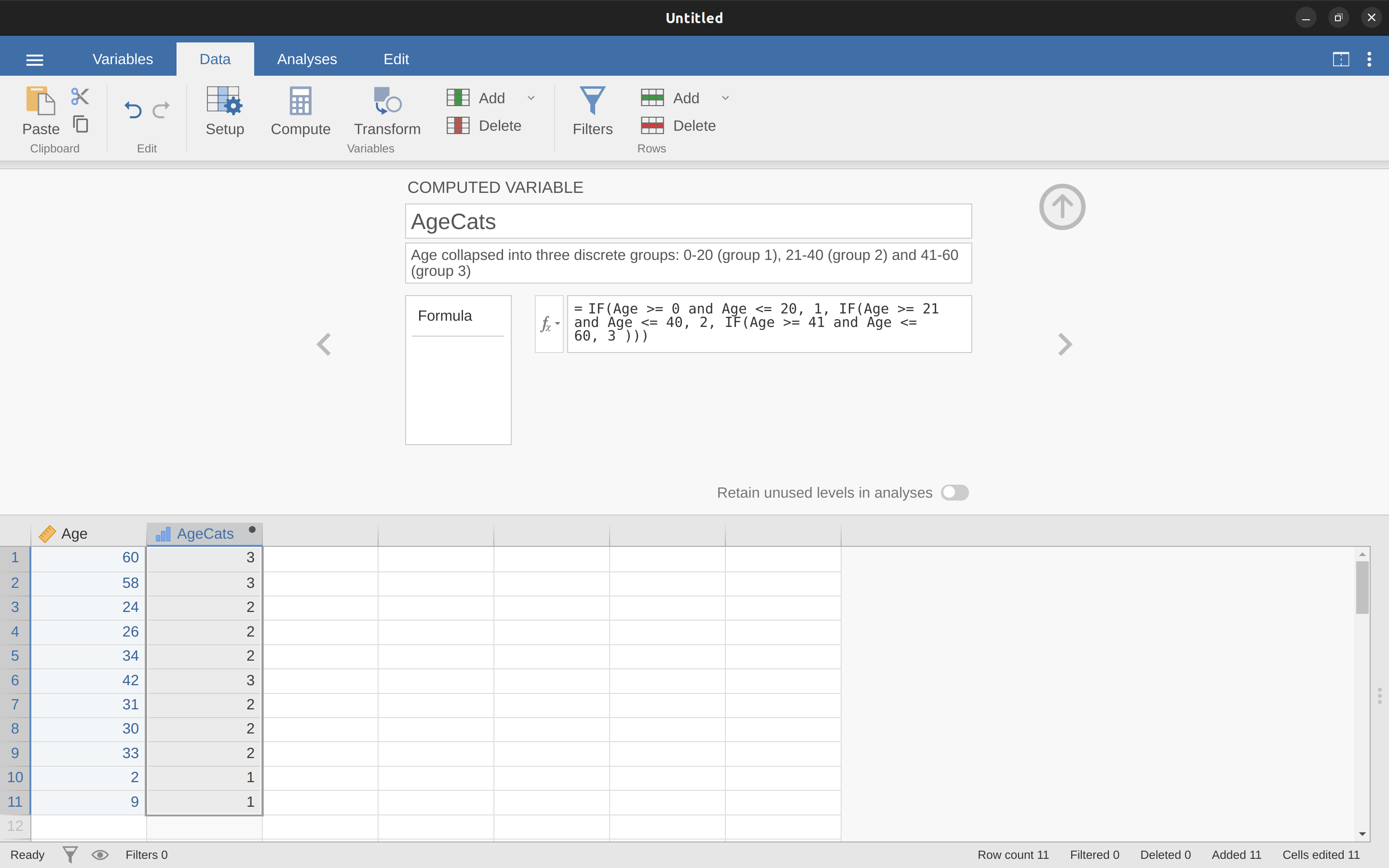
IF(Edad >= 0 y Edad <= 20, 1, IF(Edad >= 21 y Edad <= 40, 2, IF(Edad >= 41 y Edad <= 60, 3 )))
Ten en cuenta que se utilizan tres paréntesis izquierdos durante el anidamiento, por lo que todo el enunciado debe terminar con tres paréntesis derechos; de lo contrario, obtendrás un mensaje de error. La captura de pantalla jamovi para esta manipulación de datos, junto con una tabla de frecuencias adjunta, se muestra en Figure 6.6.
Es importante dedicar tiempo a averiguar si las categorías resultantes tienen algún sentido para tu proyecto de investigación. Si no tienen ningún sentido para ti como categorías significativas, es probable que cualquier análisis de datos que utilice esas categorías no tenga ningún sentido. De forma más general, en la práctica, he observado que la gente tiene un fuerte deseo de dividir sus datos (continuos y desordenados) en unas pocas categorías (discretas y simples), y luego ejecutar análisis utilizando los datos categorizados en lugar de los datos originales.8 No me atrevería a decir que se trata de una idea intrínsecamente mala, pero a veces tiene algunos inconvenientes bastante graves, por lo que te aconsejaría cierta cautela si estás pensando en hacerlo.
6.3.3 Crear una transformación que puedea aplicarse a múltiples variables
A veces se desea aplicar la misma transformación a más de una variable, por ejemplo, cuando tienes varios elementos del cuestionario que deben volver a calcularse o codificarse de la misma manera. Y una de las características interesantes de jamovi es que puede crear una transformación, usando el botón ‘Datos’ - ‘Transformar’, que luego se puede guardar y aplicar a múltiples variables. Volvamos al primer ejemplo anterior, usando el archivo de datos likert.omv que contiene una sola variable con respuestas de escala Likert brutas para 10 personas. Para crear una transformación que puedas guardar y luego aplicar en múltiples variables (suponiendo que tengas más variables como esta en tu archivo de datos), primero en el editor de hojas de cálculo, selecciona (es decir, haz clic) la variable que quieres usar para crear inicialmente la transformación. En nuestro ejemplo, esto es likert.raw. A continuación, haz clic en el botón ‘Transformar’ en la cinta ‘Datos’ de jamovi y verás algo como Figure 6.7.
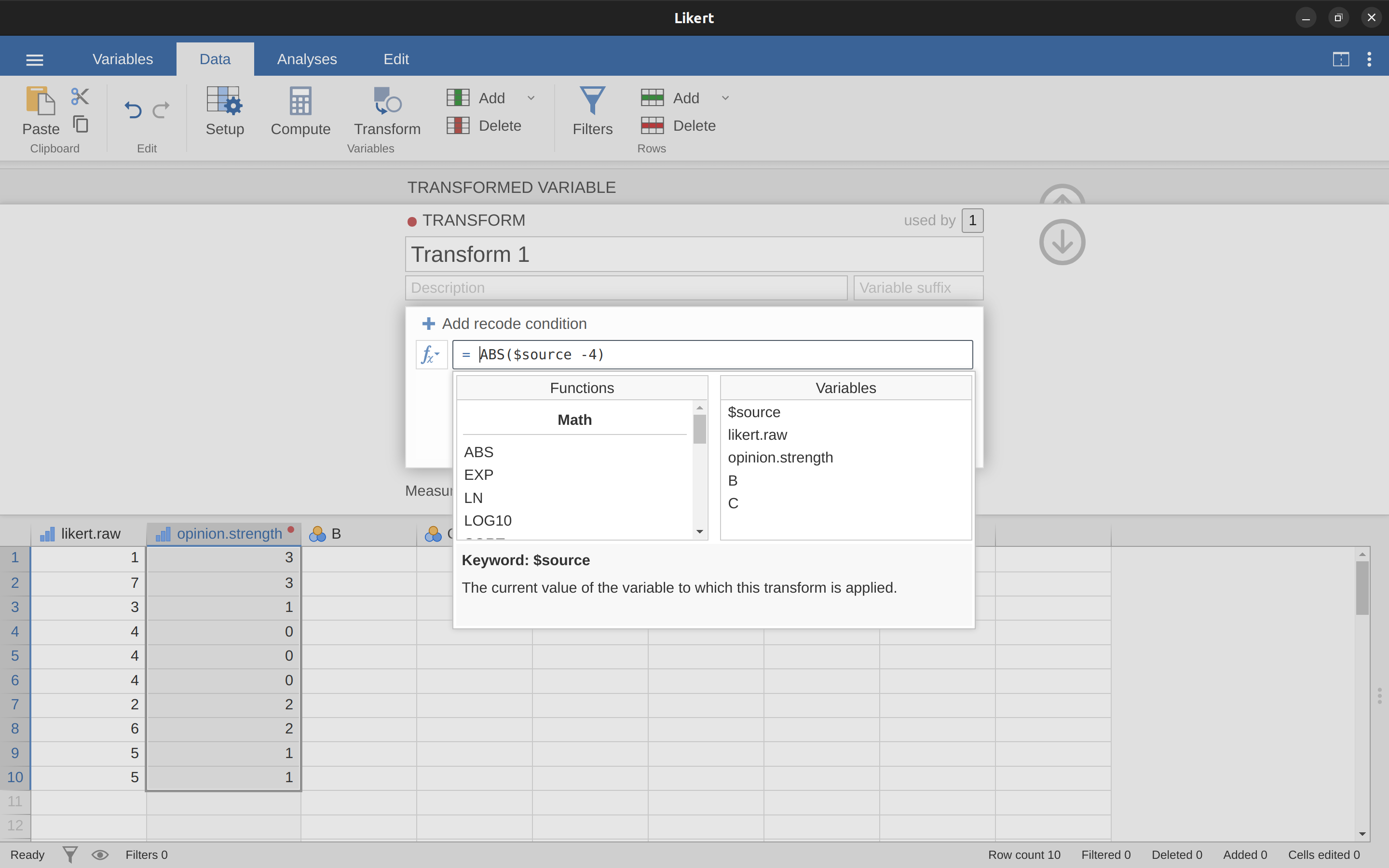
Asigna un nombre a tu nueva variable, llamémosla opinion.strength y luego haz clic en el cuadro de selección ‘usar transformación’ y selecciona ‘Crear nueva transformación…’. Aquí es donde crearás y nombrarás la transformación que se puede volver a aplicar a tantas variables como quieras. La transformación se nombra automáticamente para nosotros como ‘Transformar 1’ (imaginativo, eh. Puedes cambiarlo si quieres). Luego escribe la expresión “ABS($source - 4)” en el cuadro de texto de la función, como en Figure 6.8, presiona Entrar o Retorno en tu teclado y listo, has creado una nueva transformación y la has aplicado a la variable likert.raw. Bien, eh. Ten en cuenta que en lugar de usar la etiqueta de la variable en la expresión, hemos usado ‘$source’. Esto es para que podamos usar la misma transformación con tantas variables diferentes como queramos; jamovi requiere que uses ‘$source’ para referirte a la variable de origen que estás transformando. Tu transformación también se ha guardado y se puede reutilizar en cualquier momento que quieras (siempre que guardes el conjunto de datos como un archivo ‘.omv’; de lo contrario, ¡lo perderás!).
También puedes crear una transformación con el segundo ejemplo que vimos, la distribución por edades de las personas en una reunión social. ¡Adelante, sabes que quieres hacerlo! Recuerda que dividimos esta variable en tres grupos: joven, adulto y mayor. Esta vez vamos a conseguir lo mismo, pero usando el botón jamovi ‘Transformar’ - ‘Agregar condición de recodificación’. Con este conjunto de datos (vuelve a él o créalo de nuevo si no lo guardaste) configura una nueva transformación de variable. Llama a la variable transformada AgeCats y la transformación que crearás Agegroupings. Luego haga clic en el gran signo “\(+\)” al lado del cuadro de función. Este es el botón ‘Agregar condición’ y he pegado una gran flecha roja en Figure 6.9 para que puedas ver exactamente dónde está. Vuelve a crear la transformación que se muestra en Figure 6.9 y cuando hayas terminado, verás que aparecen los nuevos valores en la ventana de la hoja de cálculo. Además, la transformación de grupos de edad se ha guardado y se puede volver a aplicar en el momento que quieras. Ok, sé que es poco probable que tengas más de una variable ‘Edad’, pero ahora ya entiendes cómo configurar transformaciones en jamovi, así que puedes seguir esta idea con otros tipos de variables. Un escenario típico para esto es cuando tienes una escala de cuestionario con, digamos, 20 ítems (variables) y cada ítem se calificó originalmente de 1 a 6 pero, por alguna razón o peculiaridad de los datos, decides volver a codificar todos los ítems como 1 a 3. Puedes hacerlo fácilmente en jamovi creando y luego volviendo a aplicar tu transformación para cada variable que quieras recodificar.
| function | example input | (answer) | |
|---|---|---|---|
| square root | SQRT(x) | SQRT(25) | 5 |
| absolute value | ABS(x) | ABS(-23) | 23 |
| logarithm (base 10) | LOG10(x) | LOG10(1000) | 3 |
| logarithm (base e) | LN(x) | LN(1000) | 6.91 |
| exponentiation | EXP(x) | EXP(6.908) | 1e+03 |
| box-cox | BOXCOX(x, lamda) | BOXCOX(6.908, 3) | 110 |
6.4 Otras funciones y operaciones matemáticas
En la sección sobre Transformar y recodificar una variable, analicé las ideas detrás de las transformaciones de variables y mostré que muchas de las transformaciones que podrías querer aplicar a tus datos se basan en funciones y operaciones matemáticas bastante simples. En esta sección quiero volver a esa discusión y mencionar otras funciones matemáticas y operaciones aritméticas que en realidad son bastante útiles para muchos análisis de datos del mundo real. Table 6.5 ofrece una breve descripción general de las diversas funciones matemáticas de las que quiero hablar aquí o más adelante. 9 Obviamente, esto ni siquiera se acerca a la catalogación de la gama de posibilidades disponibles, pero sí cubre una gama de funciones que se utilizan regularmente en el análisis de datos y que están disponibles en jamovi.
6.4.1 Logaritmos y exponenciales
Como mencioné anteriormente, jamovi tiene una gama útil de funciones matemáticas incorporadas y no tendría mucho sentido intentar describirlas o enumerarlas todas. Me he centrado mayoritariamente en aquellas funciones que son estrictamente necesarias para este libro. Sin embargo, quiero hacer una excepción con logaritmos y exponenciales. Aunque no se necesitan en ninguna otra parte de este libro, están en todas partes en la estadística en general. Y no solo eso, hay muchas situaciones en las que es conveniente analizar el logaritmo de una variable (es decir, hacer una “transformación logarítmica” de la variable). Sospecho que muchos (quizás la mayoría) de los lectores de este libro se habrán encontrado con logaritmos y exponenciales antes, pero por experiencias pasadas sé que hay una proporción sustancial de estudiantes que asisten a una clase de estadística en ciencias sociales que no han tocado los logaritmos desde el instituto, y que agradecerían un repaso.
Para entender logaritmos y exponenciales, lo más fácil es calcularlos y ver cómo se relacionan con otros cálculos simples. Hay tres funciones jamovi en particular de las que quiero hablar, a saber, LN(), LOG10() y EXP(). Para empezar, consideremos LOG10(), que se conoce como el “logaritmo en base 10”. El truco para entender un logaritmo es entender que es básicamente lo “opuesto” a una potencia. Específicamente, el logaritmo en base 10 está estrechamente relacionado con las potencias de 10. Comencemos notando que 10 al cubo es 1000. Matemáticamente, escribiríamos esto:
\[10^3=1000\]
El truco para entender un logaritmo es reconocer que la afirmación de que “10 elevado a 3 es igual a 1000” es equivalente a la afirmación de que “el logaritmo (en base 10) de 1000 es igual a 3”. Matemáticamente, lo escribimos de la siguiente manera,
\[\log_{10}(1000)=3\]
Bien, puesto que la función LOG10() está relacionada con las potencias de 10, es de esperar que haya otros logaritmos (en bases distintas de 10) que también estén relacionados con otras potencias. Y, por supuesto, es cierto: en realidad el número 10 no tiene nada de especial desde el punto de vista matemático. Nos resulta útil porque los números decimales se construyen alrededor del número 10, pero el malvado mundo de las matemáticas se burla de nuestros números decimales. Lamentablemente, al universo no le importa cómo escribimos los números. La consecuencia de esta indiferencia cósmica es que no tiene nada de especial calcular logaritmos en base 10. Podrías, por ejemplo, calcular tus logaritmos en base 2. Alternativamente, un tercer tipo de logaritmo, y que vemos mucho más en estadística que la base 10 o la base 2, se llama logaritmo natural y corresponde al logaritmo en base e. Como es posible que algún día te encuentres con él, mejor te explico qué es e. El número e, conocido como número de Euler, es uno de esos molestos números “irracionales” cuya expansión decimal es infinitamente larga, y se considera uno de los números más importantes de las matemáticas. Los primeros dígitos de e son:
\[e \approx 2.718282 \]
Hay bastantes situaciones en estadística que requieren que calculemos potencias de \(e\), aunque ninguna de ellas aparece en este libro. Elevar \(e\) a la potencia \(x\) se denomina exponencial de \(x\), por lo que es muy común ver \(e^x\) escrito como \(\exp(x)\). Así que no es de extrañar que jamovi tenga una función que calcula exponenciales, llamada EXP(). Como el número \(e\) aparece tan a menudo en estadística, el logaritmo natural (es decir, el logaritmo en base \(e\)) también tiende a aparecer. Los matemáticos suelen escribirlo como \(\log_e(x)\) o \(\ln(x)\). De hecho, jamovi funciona de la misma manera: la función LN() corresponde al logaritmo natural.
Y con eso, creo que ya hemos tenido suficientes exponenciales y logaritmos para este libro.
6.5 Extracción de un subconjunto de datos
Un tipo de tratamiento de datos muy importante es poder extraer un subconjunto concreto de datos. Por ejemplo, es posible que solo te interese analizar los datos de una condición experimental, o puedes querer observar de cerca los datos de personas mayores de 50 años. Para hacer esto, el primer paso es hacer que jamovi filtre el subconjunto de datos correspondientes a las observaciones que te interesan.
Esta sección vuelve al conjunto de datos nightgarden.csv. Si estás leyendo todo este capítulo de una sola vez, entonces ya deberías tener este conjunto de datos cargado en una ventana jamovi. Para esta sección, vamos a centrarnos en las dos variables locutor y enunciado (consulta Tabulación y tabulación cruzada de datos si has olvidado cómo son estas variables). Supongamos que lo que queremos es extraer solo las frases pronunciadas por Makka-Pakka. Para ello, tenemos que especificuniversity holidaysar un filtro en jamovi. En primer lugar, abre una ventana de filtro haciendo clic en ‘Filtros’ en la barra de herramientas principal de ‘Datos’ de jamovi. A continuauniversity holidaysción, en el cuadro de texto ‘Filtro 1’, junto al signo ‘=’, escribe lo siguiente:
locutor == ‘makka-pakka’
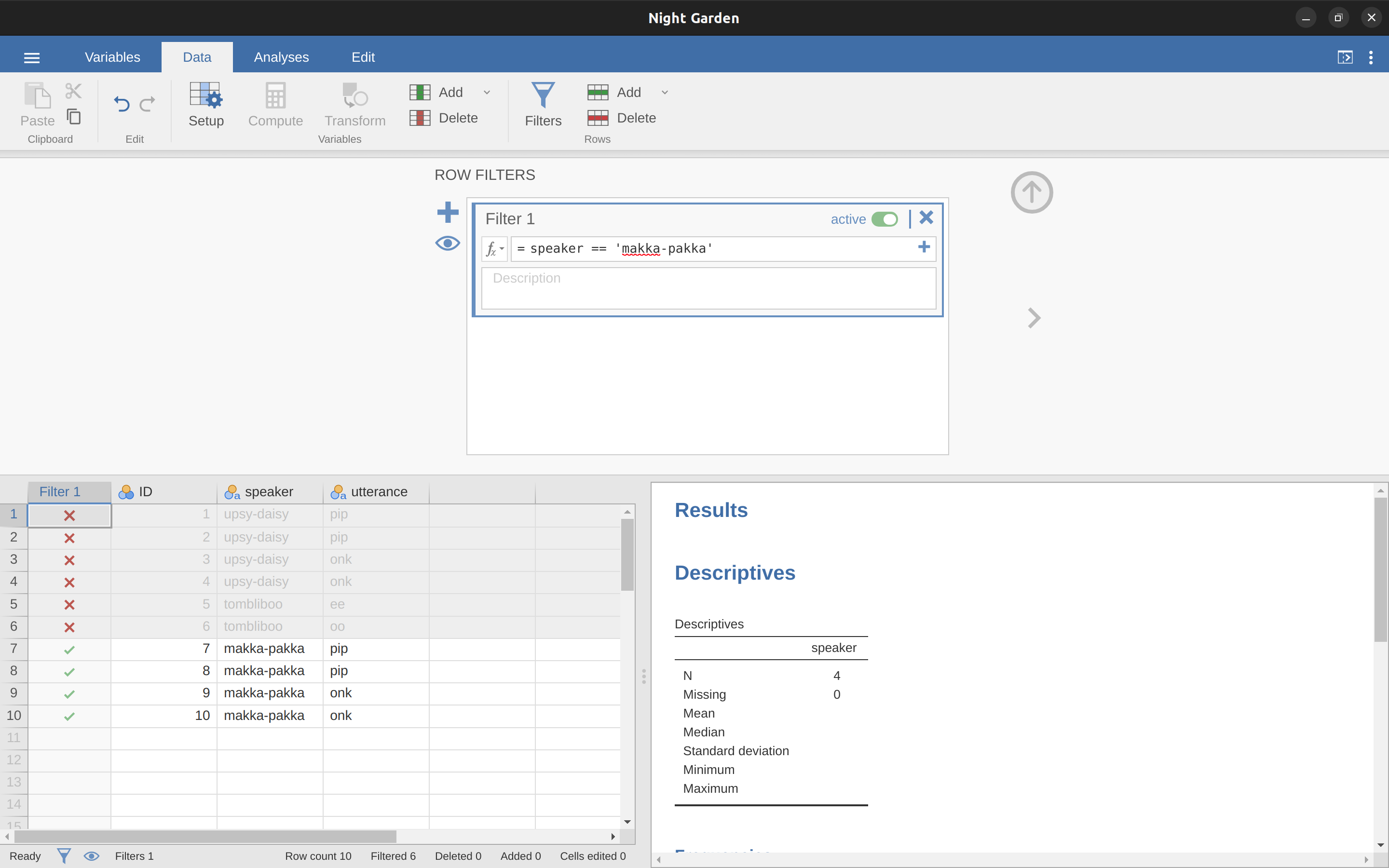
Cuando lo hayas hecho, verás que se ha añadido una nueva columna a la ventana de la hoja de cálculo (véase Figure 6.10), etiquetada como ‘Filtro 1’, con los casos en los que el locutor no es ‘makka-pakka’ en gris (es decir, filtrado) y, por el contrario, los casos en los que el locutor es ‘makka-pakka’ tienen una marca de verificación verde que indica que están filtrados. Puedes comprobarlo ejecutando ‘Exploración’ - ‘Descriptivos’ - ‘Tablas de frecuencia’ para la variable locutor y ver qué muestra. Pruébalo.
A partir de este sencillo ejemplo, también puedes crear filtros más complejos utilizando expresiones lógicas en jamovi. Por ejemplo, supongamos que quisieras mantener solo aquellos casos en los que el enunciado es “pip” o “oo”. En este caso, en el cuadro de texto ‘Filtro 1’, junto al signo ‘=’, escribirías lo siguiente:
enunciado == ‘pip’ o enunciado == ‘oo’
6.6 Resumen
Obviamente, este capítulo no tiene ninguna coherencia. No es más que un conjunto de temas y trucos que puede ser útil conocer, así que lo mejor que puedo hacer es repetir esta lista:
- Tabulación y tabulación cruzada de datos
- Expresiones lógicas en jamovi
- Transformar y recodificar una variable
- Otras funciones y operaciones matemáticas
- [Extracción de un subconjunto de los datos]
La cita proviene de Home is the Hangman, publicado en 1975.↩︎
Ofrezco mis intentos de adolescente de ser “cool” como evidencia de que algunas cosas simplemente no se pueden hacer.↩︎
puedes hacer esto en la pantalla Calcular nueva variable, ¡aunque calcular 2 + 2 para cada celda de una nueva variable no es muy útil!↩︎
Ten en cuenta que este es un operador muy diferente al operador de igualdad =. Un error tipográfico común que se comete cuando se intentan escribir comandos lógicos en jamovi (u otros idiomas, ya que la distinción “= versus ==” es importante en muchos programas informáticos y estadísticos) es escribir accidentalmente = cuando realmente quieres decir ==. Ten especial cuidado con esto, he estado programando en varios lenguajes desde que era adolescente y todavía me equivoco mucho. Mmm. Creo que veo por qué no era guay cuando era adolescente. Y por qué todavía sigo sin molar.↩︎
He aquí una peculiaridad en jamovi. Cuando tenemos expresiones lógicas simples como las que ya hemos visto, por ejemplo, 2 + 2 == 5, jamovi indica claramente ‘falso’ (o ‘verdadero’) en la columna correspondiente de la hoja de cálculo. En realidad, jamovi almacena ‘falso’ como 0 y ‘verdadero’ como 1. Cuando tenemos expresiones lógicas más complejas, como (2+2 == 4) o (2+2 == 5), jamovi simplemente muestra 0 o 1, dependiendo de si la expresión lógica se evalúa como falsa o verdadera.↩︎
El valor absoluto de un número es su distancia al cero, independientemente de si su signo es negativo o positivo.↩︎
la razón por la que tenemos que usar el comando ‘IF’ y mantener cero como cero es que no puedes simplemente usar likert.centred / opinion.strength para calcular el signo de likert.centred, porque dividir matemáticamente cero por cero no funciona. Pruébalo y verás↩︎
si has leído más en el libro y estás releyendo esta sección, entonces un buen ejemplo de esto sería alguien que elige hacer un ANOVA usando AgeCats como la variable de agrupación, en lugar de ejecutar una regresión utilizando la edad como predictor. A veces hay buenas razones para hacer esto. Por ejemplo, si la relación entre la edad y tu variable de resultado es altamente no lineal y no te sientes cómoda intentando ejecutar una regresión no lineal. Sin embargo, a menos que realmente tengas una buena razón para hacerlo, es mejor no hacerlo. Tiende a introducir todo tipo de problemas (p. ej., los datos probablemente violarán la suposición de normalidad) y puedes perder mucho poder estadístico.↩︎
Dejaremos la función box-cox para más adelante↩︎