| Hypothesis | Degree of Belief |
|---|---|
| Rainy day | 0.15 |
| Dry day | 0.85 |
16 Estadística bayesianas
“En nuestros razonamientos relativos a los hechos, hay todos los grados imaginables de seguridad, desde la certeza más alta hasta la especie más baja de evidencia moral. Por lo tanto, un hombre sabio proporciona su creencia a la evidencia”.
– David Hume 1
Las ideas que le he presentado en este libro describen la estadística inferencial desde la perspectiva frecuentista. No estoy solo en hacer esto. De hecho, casi todos los libros de texto que se entregan a los estudiantes de psicología presentan las opiniones del estadístico frecuentista como la teoría de la estadística inferencial, la única forma verdadera de hacer las cosas. He enseñado de esta manera por razones prácticas. La visión frecuentista de la estadística dominó el campo académico de la estadística durante la mayor parte del siglo XX, y este dominio es aún más extremo entre los científicos aplicados. Era y es una práctica corriente entre los psicólogos utilizar métodos frecuentistas. Debido a que los métodos frecuentistas son omnipresentes en los artículos científicos, todos los estudiantes de estadística deben comprender esos métodos, de lo contrario, ¡no podrán entender lo que dicen esos artículos! Desafortunadamente, al menos en mi opinión, la práctica actual en psicología a menudo está equivocada y la dependencia de los métodos frecuentistas es en parte culpable. En este capítulo explico por qué pienso esto y ofrezco una introducción a la estadística bayesiana, un enfoque que creo que es generalmente superior al enfoque ortodoxo.
Este capítulo viene en dos partes. En las primeras tres secciones, hablo de qué se tratan las estadísticas bayesianas, cubriendo las reglas matemáticas básicas de cómo funciona, así como una explicación de por qué creo que el enfoque bayesiano es tan útil. Luego, proporciono una breve descripción general de cómo puede hacer pruebas t bayesianas.
16.1 Razonamiento probabilístico por agentes racionales
Desde una perspectiva bayesiana, la inferencia estadística tiene que ver con la revisión de creencias. Comienzo con un conjunto de hipótesis candidatas h sobre el mundo. No sé cuál de estas hipótesis es verdadera, pero tengo algunas creencias sobre qué hipótesis son plausibles y cuáles no. Cuando observo los datos, d, tengo que revisar esas creencias. Si los datos son consistentes con una hipótesis, mi creencia en esa hipótesis se fortalece. Si los datos son inconsistentes con la hipótesis, mi creencia en esa hipótesis se debilita. ¡Eso es todo! Al final de esta sección, daré una descripción precisa de cómo funciona el razonamiento bayesiano, pero primero quiero trabajar con un ejemplo simple para presentar las ideas clave. Considere el siguiente problema de razonamiento.
Llevo un paraguas. ¿Crees que lloverá?
En este problema te he presentado un solo dato (d = llevo el paraguas) y te pido que me digas tu creencia o hipótesis sobre si está lloviendo. Tienes dos alternativas, h: o lloverá hoy o no lloverá. ¿Cómo deberías resolver este problema?
16.1.1 Prioridades: lo que creías antes
Lo primero que debes hacer es ignorar lo que te dije sobre el paraguas y escribir tus creencias preexistentes sobre la lluvia. Esto es importante. Si desea ser honesto acerca de cómo sus creencias han sido revisadas a la luz de nueva evidencia (datos), entonces debe decir algo sobre lo que creía antes de que aparecieran esos datos. Entonces, ¿qué podrías creer acerca de si lloverá hoy? Probablemente sepa que vivo en Australia y que gran parte de Australia es cálida y seca. La ciudad de Adelaide donde vivo tiene un clima mediterráneo, muy similar al sur de California, el sur de Europa o el norte de África. Estoy escribiendo esto en enero, así que puedes asumir que estamos en pleno verano. De hecho, es posible que haya decidido echar un vistazo rápido a Wikipedia2 y haya descubierto que Adelaida recibe un promedio de 4,4 días de lluvia durante los 31 días de enero. Sin saber nada más, puede concluir que la probabilidad de lluvia en enero en Adelaide es de alrededor del 15 % y la probabilidad de un día seco es del 85 % (consulte Table 16.1). Si esto es realmente lo que crees sobre las lluvias en Adelaide (y ahora que te lo he dicho, apuesto a que esto realmente es lo que crees), entonces lo que he escrito aquí es tu distribución anterior, escrita $ P(h)$.
16.1.2 Probabilidades: teorías sobre los datos
Para resolver el problema de razonamiento necesitas una teoría sobre mi comportamiento. ¿Cuándo lleva Dan un paraguas? Podrías adivinar que no soy un completo idiota, 3 y trato de llevar paraguas solo en días lluviosos. Por otro lado, también sabes que tengo niños pequeños, y no te sorprendería tanto saber que soy bastante olvidadizo con este tipo de cosas. Supongamos que en los días de lluvia recuerdo mi paraguas alrededor del 30% del tiempo (realmente soy terrible en esto). Pero digamos que en los días secos solo tengo un 5% de probabilidades de llevar un paraguas. Así que podría escribir esto como en Table 16.2.
| Data | Data | |
|---|---|---|
| Hypothesis | Umbrella | No umbrella |
| Rainy day | 0.30 | 0.70 |
| Dry day | 0.05 | 0.95 |
Es importante recordar que cada celda de esta tabla describe sus creencias sobre qué datos d se observarán, dada la verdad de una hipótesis particular \(h\). Esta “probabilidad condicional” se escribe \(P(d|h)\), que se puede leer como “la probabilidad de \(d\) dada \(h\)”. En las estadísticas bayesianas, esto se conoce como la probabilidad de los datos \(d\) dada la hipótesis \(h\).4
16.1.3 La probabilidad conjunta de datos e hipótesis
En este punto todos los elementos están en su lugar. Habiendo anotado los antecedentes y la probabilidad, tiene toda la información que necesita para hacer un razonamiento bayesiano. La pregunta ahora es ¿cómo usamos esta información? Resulta que hay una ecuación muy simple que podemos usar aquí, pero es importante que comprenda por qué la usamos, así que intentaré desarrollarla a partir de ideas más básicas.
Comencemos con una de las reglas de la teoría de la probabilidad. Lo enumeré en Table 7.1, pero no le di mucha importancia en ese momento y probablemente lo ignoraste. La regla en cuestión es la que habla de la probabilidad de que dos cosas sean ciertas. En nuestro ejemplo, es posible que desee calcular la probabilidad de que hoy llueva (es decir, la hipótesis h es verdadera) y llevo un paraguas (es decir, se observan los datos \(d\)). La probabilidad conjunta de la hipótesis y los datos se escribe \(P(d,h)\), y se puede calcular multiplicando la anterior \(P(h)\) por la probabilidad \(P(d|h)\) . Matemáticamente, decimos que
\[P(d,h)=P(d|h)P(h)\]
Entonces, ¿cuál es la probabilidad de que hoy sea un día lluvioso y me acuerde de llevar un paraguas? Como comentamos anteriormente, el anterior nos dice que la probabilidad de un día lluvioso es del 15 %, y la probabilidad nos dice que la probabilidad de que me acuerde de mi paraguas en un día lluvioso es de \(30\%\). Entonces, la probabilidad de que ambas cosas sean ciertas se calcula multiplicando las dos
\[ \begin{split} P(lluvia, paraguas) & = P(paraguas|lluvia) \times P(lluvia) \\ & = 0.30 \times 0.15 \\ & = 0.045 \end{split} \]
En otras palabras, antes de que te digan nada de lo que realmente pasó, piensas que hay un 4,5% de probabilidad de que hoy sea un día lluvioso y que me acuerde de un paraguas. Sin embargo, por supuesto, hay cuatro cosas posibles que podrían suceder, ¿verdad? Así que repitamos el ejercicio para los cuatro. Si hacemos eso, terminamos con Table 16.3.
| Umbrella | No-umbrella | |
|---|---|---|
| Rainy | 0.045 | 0.105 |
| Dry | 0.0425 | 0.807 |
Esta tabla captura toda la información sobre cuál de las cuatro posibilidades es probable. Sin embargo, para obtener realmente una imagen completa, es útil sumar los totales de las filas y los totales de las columnas. Eso nos da Table 16.4.
| Umbrella | No-umbrella | Total | |
|---|---|---|---|
| Rainy | 0.045 | 0.105 | 0.15 |
| Dry | 0.0425 | 0.807 | 0.85 |
| Total | 0.0875 | 0.912 | 1 |
Esta es una tabla muy útil, por lo que vale la pena tomarse un momento para pensar en lo que nos dicen todos estos números. Primero, observe que las sumas de las filas no nos dicen nada nuevo en absoluto. Por ejemplo, la primera fila nos dice que si ignoramos todo este asunto de los paraguas, la probabilidad de que hoy sea un día lluvioso es del 15 %. Eso no es sorprendente, por supuesto, ya que es nuestro anterior.5 Lo importante no es el número en sí. Más bien, lo importante es que nos da cierta confianza en que nuestros cálculos son sensatos. Ahora eche un vistazo a las sumas de las columnas y observe que nos dicen algo que aún no hemos declarado explícitamente. De la misma manera que las sumas de las filas nos dicen la probabilidad de lluvia, las sumas de las columnas nos dicen la probabilidad de que lleve un paraguas. En concreto, la primera columna nos dice que de media (es decir, ignorando si es un día lluvioso o no) la probabilidad de que lleve paraguas es del 8,75%. Finalmente, observe que cuando sumamos los cuatro eventos lógicamente posibles, todo suma 1. En otras palabras, lo que hemos escrito es una distribución de probabilidad adecuada definida sobre todas las combinaciones posibles de datos e hipótesis.
Ahora, debido a que esta tabla es tan útil, quiero asegurarme de que comprenda a qué corresponden todos los elementos y cómo se escribieron (Table 16.5):
| Umbrella | No-umbrella | ||
|---|---|---|---|
| Rainy | P(Umbrella, Rainy) | P(No-umbrella, Rainy) | P(Rainy) |
| Dry | P(Umbrella, Dry) | P(No-umbrella, Dry) | P(Dry) |
| P(Umbrella) | P(No-umbrella) |
Finalmente, usemos la notación estadística “adecuada”. En el problema del día de lluvia, los datos corresponden a la observación de que tengo o no tengo paraguas. Así que dejaremos que \(d_1\) se refiera a la posibilidad de que me observes con un paraguas, y \(d_2\) se refiera a que me observes sin uno. De manera similar, \(h_1\) es tu hipótesis de que hoy llueve, y \(h_2\) es la hipótesis de que no. Usando esta notación, la tabla se parece a Table 16.6.
| \( d_1 \) | \( d_2 \) | ||
|---|---|---|---|
| \( h_1 \) | \(P(h_1, d_1)\) | \(P(h_1, d_2)\) | \( P(h_1) \) |
| \( h_2 \) | \(P(h_2, d_1)\) | \(P(h_2, d_2)\) | \( P(h_2) \) |
| \( P(d_1) \) | \( P(d_2) \) |
16.1.4 Actualización de creencias usando la regla de Bayes
La tabla que presentamos en la última sección es una herramienta muy poderosa para resolver el problema del día lluvioso, ya que considera las cuatro posibilidades lógicas y establece exactamente qué tan seguro está en cada una de ellas antes de recibir datos. Ahora es el momento de considerar qué sucede con nuestras creencias cuando en realidad se nos dan los datos. En el problema del día lluvioso, se le dice que realmente llevo un paraguas. Esto es algo así como un evento sorprendente. Según nuestra tabla, la probabilidad de que lleve un paraguas es solo del 8,75 %. Pero eso tiene sentido, ¿verdad? Una mujer que lleva un paraguas en un día de verano en una ciudad calurosa y seca es bastante inusual, por lo que realmente no esperabas eso. Sin embargo, los datos te dicen que es cierto. No importa cuán improbable pensara que era, ahora debe ajustar sus creencias para adaptarse al hecho de que ahora sabe que tengo un paraguas.6 Para reflejar este nuevo conocimiento, nuestra tabla revisada debe tener los siguientes números. (ver Table 16.7).
| Umbrella | No-umbrella | |
|---|---|---|
| Rainy | 0 | |
| Dry | 0 | |
| Total | 1 | 0 |
En otras palabras, los hechos han eliminado cualquier posibilidad de “sin paraguas”, por lo que tenemos que poner ceros en cualquier celda de la tabla que implique que no llevo paraguas. Además, sabes con certeza que llevo un paraguas, por lo que la suma de la columna de la izquierda debe ser 1 para describir correctamente el hecho de que \(P(paraguas) = 1\).
¿Qué dos números debemos poner en las celdas vacías? Una vez más, no nos preocupemos por las matemáticas y, en su lugar, pensemos en nuestras intuiciones. Cuando escribimos nuestra tabla por primera vez, resultó que esas dos celdas tenían números casi idénticos, ¿verdad? Calculamos que la probabilidad conjunta de “lluvia y paraguas” era del 4,5 %, y la probabilidad conjunta de “seco y paraguas” era del 4,25 %. En otras palabras, antes de que te dijera que de hecho llevo un paraguas, habrías dicho que estos dos eventos eran casi idénticos en probabilidad, ¿no? Pero observe que ambas posibilidades son consistentes con el hecho de que en realidad llevo un paraguas. Desde la perspectiva de estas dos posibilidades, muy poco ha cambiado. Espero que esté de acuerdo en que sigue siendo cierto que estas dos posibilidades son igualmente plausibles. Entonces, lo que esperamos ver en nuestra tabla final son algunos números que preservan el hecho de que “lluvia y paraguas” es ligeramente más plausible que “seco y paraguas”, al mismo tiempo que asegura que los números en la tabla suman. ¿Algo como Table 16.8, quizás?
| Umbrella | No-umbrella | |
|---|---|---|
| Rainy | 0.514 | 0 |
| Dry | 0.486 | 0 |
| Total | 1 | 0 |
Lo que esta tabla te está diciendo es que, después de que te digan que llevo un paraguas, crees que hay un 51,4 % de posibilidades de que hoy sea un día lluvioso y un 48,6 % de que no. ¡Esa es la respuesta a nuestro problema! La probabilidad posterior de que llueva \(P(h\|d)\) dado que llevo paraguas es del 51,4%
¿Cómo calculé estos números? Probablemente puedas adivinar. Para calcular que había una probabilidad de \(0.514\) de “lluvia”, todo lo que hice fue tomar la probabilidad de \(0.045\) de “lluvia y paraguas” y dividirla por la probabilidad de \(0.0875\) de “paraguas”. Esto produce una tabla que satisface nuestra necesidad de que todo sume 1 y nuestra necesidad de no interferir con la verosimilitud relativa de los dos eventos que en realidad son consistentes con los datos. Para decir lo mismo usando la jerga estadística sofisticada, lo que he hecho aquí es dividir la probabilidad conjunta de la hipótesis y los datos \(P(d, h)\) por la probabilidad marginal de los datos \(P(d )\), y esto es lo que nos da la probabilidad posterior de la hipótesis dados los datos que se han observado. Para escribir esto como una ecuación: 7
\[P(h|d)=\frac{P(d,h)}{P(d)}\]
Sin embargo, recuerda lo que dije al comienzo de la última sección, a saber, que la probabilidad conjunta \(P(d, h)\) se calcula multiplicando el Pphq anterior por la probabilidad \(P(d|h)\). En la vida real, las cosas que realmente sabemos escribir son los antecedentes y la probabilidad, así que volvamos a sustituirlos en la ecuación. Esto nos da la siguiente fórmula para la probabilidad posterior:
\[P(h|d)=\frac{P(d|h)P(h)}{P(d)}\]
Y esta fórmula, amigos, se conoce como regla de Bayes. Describe cómo un alumno comienza con creencias previas sobre la plausibilidad de diferentes hipótesis y le dice cómo se deben revisar esas creencias frente a los datos. En el paradigma bayesiano, todas las inferencias estadísticas fluyen de esta regla simple.
16.2 Pruebas de hipótesis bayesianas
En Chapter 9 describí el enfoque ortodoxo para la prueba de hipótesis. Tomó un capítulo entero para describirlo, porque la prueba de hipótesis nula es un artilugio muy elaborado que a la gente le resulta muy difícil entender. Por el contrario, el enfoque bayesiano para la prueba de hipótesis es increíblemente simple. Escojamos un escenario que sea muy parecido al escenario ortodoxo. Hay dos hipótesis que queremos comparar, una hipótesis nula \(h_0\) y una hipótesis alternativa \(h_1\). Antes de ejecutar el experimento, tenemos algunas creencias \(P(h)\) sobre qué hipótesis son verdaderas. Realizamos un experimento y obtenemos datos d. A diferencia de la estadística frecuentista, la estadística bayesiana sí nos permite hablar de la probabilidad de que la hipótesis nula sea cierta. Mejor aún, nos permite calcular la probabilidad posterior de la hipótesis nula, usando la regla de Bayes:
\[P(h_0|d)=\frac{P(d|h_0)P(h_0)}{P(d)}\]
Esta fórmula nos dice exactamente cuánta creencia debemos tener en la hipótesis nula después de haber observado los datos d. De manera similar, podemos calcular cuánta creencia colocar en la hipótesis alternativa usando esencialmente la misma ecuación. Todo lo que hacemos es cambiar el subíndice
\[P(h_1|d)=\frac{P(d|h_1)P(h_1)}{P(d)}\]
Es todo tan simple que me siento como un idiota incluso molestándome en escribir estas ecuaciones, ya que todo lo que estoy haciendo es copiar la regla de Bayes de la sección anterior.8
16.2.1 El factor de Bayes
En la práctica, la mayoría de los analistas de datos bayesianos tienden a no hablar en términos de probabilidades posteriores sin procesar \(P(h_0|d)\) y \(P(h_1|d)\). En cambio, tendemos a hablar en términos de la razón de probabilidades posterior. Piense en ello como apostar. Supongamos, por ejemplo, que la probabilidad posterior de la hipótesis nula es del 25 % y la probabilidad posterior de la alternativa es del 75 %. La hipótesis alternativa es tres veces más probable que la nula, por lo que decimos que las probabilidades son de 3:1 a favor de la alternativa. Matemáticamente, todo lo que tenemos que hacer para calcular las probabilidades posteriores es dividir una probabilidad posterior entre la otra
\[\frac{P(h_1|d)}{P(h_0|d)}=\frac{0.75}{0.25}=3\]
O, para escribir lo mismo en términos de las ecuaciones anteriores
\[\frac{P(h_1|d)}{P(h_0|d)}=\frac{P(d|h_1)}{P(d|h_0)} \times \frac{P(h_1)}{P(h_0)}\]
En realidad, vale la pena ampliar esta ecuación. Aquí hay tres términos diferentes que debe conocer. En el lado izquierdo, tenemos las probabilidades posteriores, que te dicen lo que crees sobre la verosimilitud relativa de la hipótesis nula y la hipótesis alternativa después de ver los datos. En el lado derecho, tenemos las cuotas previas, que indican lo que pensabas antes de ver los datos. En el medio, tenemos el factor de Bayes, que describe la cantidad de evidencia proporcionada por los datos. (Table 16.9).
| \(\frac{P(h_1|d)}{h_0|d}\) | \(=\) | \(\frac{P(d|h_1)}{d|h_0}\) | \(\times \) | \(\frac{P(h_1)}{h_0}\) |
|---|---|---|---|---|
| \(\Uparrow\) | \(\Uparrow\) | \(\Uparrow\) | ||
| Posterior odds | Bayes factor | Prior odds |
El factor de Bayes (a veces abreviado como BF) tiene un lugar especial en la prueba de hipótesis bayesiana, porque cumple una función similar al valor p en la prueba de hipótesis ortodoxa. El factor de Bayes cuantifica la fuerza de la evidencia proporcionada por los datos y, como tal, es el factor de Bayes que las personas tienden a informar cuando realizan una prueba de hipótesis bayesiana. La razón para informar los factores de Bayes en lugar de las probabilidades posteriores es que diferentes investigadores tendrán antecedentes diferentes. Algunas personas pueden tener un fuerte sesgo para creer que la hipótesis nula es verdadera, otras pueden tener un fuerte sesgo para creer que es falsa. Debido a esto, lo cortés que debe hacer un investigador aplicado es informar el factor de Bayes. De esa manera, cualquier persona que lea el periódico puede multiplicar el factor de Bayes por sus propias probabilidades previas personales, y puede calcular por sí mismo cuáles serían las probabilidades posteriores. En cualquier caso, por convención nos gusta pretender que damos igual consideración tanto a la hipótesis nula como a la alternativa, en cuyo caso la probabilidad anterior es igual a 1, y la probabilidad posterior se vuelve igual al factor de Bayes.
16.2.2 Interpretación de los factores de Bayes
Una de las cosas realmente buenas del factor de Bayes es que los números son inherentemente significativos. Si ejecuta un experimento y calcula un factor de Bayes de 4, significa que la evidencia proporcionada por sus datos corresponde a probabilidades de apuestas de 4:1 a favor de la alternativa. Sin embargo, ha habido algunos intentos de cuantificar los estándares de evidencia que se considerarían significativos en un contexto científico. Los dos más utilizados son de Jeffreys (1961) y Kass & Raftery (1995). De los dos, tiendo a preferir la tabla Kass & Raftery (1995) porque es un poco más conservadora. Así que aquí está (Table 16.10).
| Bayes factor | Interpretation |
|---|---|
| 1 - 3 | Negligible evidence |
| 3 - 20 | Positive evidence |
| 20 - 150 | Strong evidence |
| > 150 | Very strong evidence |
Y para ser perfectamente honesto, creo que incluso los estándares de Kass & Raftery (1995) están siendo un poco caritativos. Si fuera por mí, habría llamado a la categoría de “evidencia positiva” “evidencia débil”. Para mí, cualquier cosa en el rango de 3:1 a 20:1 es evidencia “débil” o “modesta” en el mejor de los casos. Pero no hay reglas estrictas y rápidas aquí. Lo que cuenta como evidencia fuerte o débil depende completamente de qué tan conservador sea usted y de los estándares en los que insista su comunidad antes de estar dispuesta a etiquetar un hallazgo como “verdadero”.
En cualquier caso, tenga en cuenta que todos los números enumerados anteriormente tienen sentido si el factor de Bayes es mayor que 1 (es decir, la evidencia favorece la hipótesis alternativa). Sin embargo, una gran ventaja práctica del enfoque bayesiano en relación con el enfoque ortodoxo es que también le permite cuantificar la evidencia del nulo. Cuando eso suceda, el factor de Bayes será menor que 1. Puede optar por informar un factor de Bayes menor que 1, pero para ser honesto, lo encuentro confuso. Por ejemplo, suponga que la probabilidad de los datos bajo la hipótesis nula \(P(d|h_0)\) es igual a 0,2, y la probabilidad correspondiente \(P(d|h_1)\) bajo la hipótesis alternativa es 0,1. Usando las ecuaciones dadas arriba, el factor de Bayes aquí sería
\[BF=\frac{P(d|h_1)}{P(d|h_0)}=\frac{0.1}{0.2}=0.5\]
Leído literalmente, este resultado dice que la evidencia a favor de la alternativa es de 0.5 a 1. Encuentro esto difícil de entender. Para mí, tiene mucho más sentido poner la ecuación “al revés” e informar la cantidad de evidencia a favor del valor nulo. En otras palabras, lo que calculamos es esto
\[BF^{'}=\frac{P(d|h_0)}{P(d|h_1)}=\frac{0.2}{0.1}=2\]
Y lo que reportaríamos es un factor de Bayes de 2:1 a favor del nulo. Mucho más fácil de entender, y puede interpretar esto usando la tabla de arriba.
16.3 ¿Por qué ser bayesiano?
Hasta este punto me he centrado exclusivamente en la lógica que sustenta las estadísticas bayesianas. Hemos hablado sobre la idea de “probabilidad como un grado de creencia” y lo que implica sobre cómo un agente racional debería razonar sobre el mundo. La pregunta que tienes que responderte a ti mismo es esta: ¿cómo quieres hacer tus estadísticas? ¿Quiere ser un estadístico ortodoxo y basarse en distribuciones muestrales y valores p para guiar sus decisiones? ¿O quiere ser bayesiano, confiando en cosas como creencias previas, factores de Bayes y las reglas para la revisión de creencias racionales? Y para ser perfectamente honesto, no puedo responder esta pregunta por ti. En última instancia, depende de lo que creas que es correcto. Es su llamada y solo su llamada. Dicho esto, puedo hablar un poco sobre por qué prefiero el enfoque bayesiano.
16.3.1 Estadísticas que significan lo que crees que significan
Sigues usando esa palabra. No creo que signifique lo que crees que significa
– Íñigo Montoya, La princesa prometida 9
Para mí, una de las mayores ventajas del enfoque bayesiano es que responde a las preguntas correctas. Dentro del marco bayesiano, es perfectamente sensato y permisible referirse a “la probabilidad de que una hipótesis sea verdadera”. Incluso puedes intentar calcular esta probabilidad. En última instancia, ¿no es eso lo que quiere que le digan sus pruebas estadísticas? Para un ser humano real, esto parecería ser el objetivo principal de hacer estadísticas, es decir, determinar qué es verdad y qué no lo es. Cada vez que no esté exactamente seguro de cuál es la verdad, debe usar el lenguaje de la teoría de la probabilidad para decir cosas como “hay un 80 % de posibilidades de que la teoría A sea cierta, pero un 20 % de posibilidades de que la teoría B sea cierta”. en cambio”.
Esto parece tan obvio para un ser humano, pero está explícitamente prohibido dentro del marco ortodoxo. Para un frecuentador, tales declaraciones son una tontería porque “la teoría es verdadera” no es un evento repetible. Una teoría es verdadera o no lo es, y no se permiten declaraciones probabilísticas, sin importar cuánto quieras hacerlas. Hay una razón por la cual, en la Sección 9.5, le advertí repetidamente que no interpretara el valor p como la probabilidad de que la hipótesis nula sea verdadera. Hay una razón por la que casi todos los libros de texto sobre estadísticas se ven obligados a repetir esa advertencia. Es porque la gente quiere desesperadamente que esa sea la interpretación correcta. A pesar del dogma frecuentista, una vida de experiencia enseñando a estudiantes universitarios y haciendo análisis de datos a diario me sugiere que la mayoría de los humanos reales piensan que “la probabilidad de que la hipótesis sea cierta” no solo es significativa, es lo que más nos importa. . Es una idea tan atractiva que incluso los estadísticos capacitados caen presa del error de tratar de interpretar un valor p de esta manera. Por ejemplo, aquí hay una cita de un informe oficial de Newspoll en 2013, que explica cómo interpretar su análisis de datos (frecuentista): 10
A lo largo del informe, en su caso, se han observado cambios estadísticamente significativos. Todas las pruebas de significación se han basado en el nivel de confianza del 95 por ciento. Esto significa que si se observa que un cambio es estadísticamente significativo, existe un 95 por ciento de probabilidad de que haya ocurrido un cambio real, y no se debe simplemente a una variación aleatoria. (énfasis añadido)
¡No! Eso no es lo que significa p < .05. Eso no es lo que significa un 95% de confianza para un estadístico frecuentista. La sección en negrita es simplemente incorrecta. Los métodos ortodoxos no pueden decirle que “hay un 95% de posibilidades de que haya ocurrido un cambio real”, porque este no es el tipo de evento al que se pueden asignar probabilidades frecuentistas. Para un frecuentador ideológico, esta frase no debería tener sentido. Incluso si eres un frecuentador más pragmático, sigue siendo la definición incorrecta de un valor p. Simplemente no está permitido o es correcto decirlo si desea confiar en las herramientas estadísticas ortodoxas.
Por otro lado, supongamos que eres bayesiano. Aunque el pasaje en negrita es la definición incorrecta de un valor p, es más o menos exactamente lo que quiere decir un bayesiano cuando dice que la probabilidad posterior de la hipótesis alternativa es superior al 95%. Y aquí está la cosa. Si el posterior bayesiano es en realidad lo que desea informar, ¿por qué está tratando de usar métodos ortodoxos? Si desea hacer afirmaciones bayesianas, todo lo que tiene que hacer es ser bayesiano y usar herramientas bayesianas.
Hablando por mí mismo, descubrí que esto es lo más liberador de cambiar a la vista bayesiana. Una vez que haya dado el salto, ya no tendrá que envolver su cabeza en definiciones contrarias a la intuición de los valores p. No tiene que molestarse en recordar por qué no puede decir que está 95% seguro de que la verdadera media se encuentra dentro de algún intervalo. Todo lo que tiene que hacer es ser honesto acerca de lo que creía antes de realizar el estudio y luego informar lo que aprendió al hacerlo. Suena bien, ¿no? Para mí, esta es la gran promesa del enfoque bayesiano. Usted hace el análisis que realmente quiere hacer y expresa lo que realmente cree que le están diciendo los datos.
16.3.2 Estándares probatorios en los que puede creer
Si \(p\) está por debajo de .02, esto indica claramente que la hipótesis \(nula\) no explica la totalidad de los hechos. No nos equivocaremos a menudo si trazamos una línea convencional en .05 y consideramos que los valores más pequeños de \(p\) indican una discrepancia real.
– Sir Ronald Fisher (Fisher, 1925)
Considere la cita anterior de Sir Ronald Fisher, uno de los fundadores de lo que se ha convertido en el enfoque ortodoxo de las estadísticas. Si alguien alguna vez ha tenido derecho a expresar una opinión sobre la función prevista de los valores p, es Fisher. En este pasaje, tomado de su guía clásica Métodos estadísticos para trabajadores de la investigación, deja bastante claro lo que significa rechazar una hipótesis nula en p < .05. En su opinión, si consideramos que p < 0,05 significa que hay “un efecto real”, entonces “no nos equivocaremos a menudo”. Esta vista no es inusual. En mi experiencia, la mayoría de los practicantes expresan puntos de vista muy similares a los de Fisher. En esencia, se supone que la convención p < .05 representa un estándar probatorio bastante estricto.
Bueno, ¿qué tan cierto es eso? Una forma de abordar esta pregunta es tratar de convertir los valores p en factores de Bayes y ver cómo se comparan los dos. No es algo fácil de hacer porque un valor p es un tipo de cálculo fundamentalmente diferente a un factor de Bayes, y no miden lo mismo. Sin embargo, ha habido algunos intentos de resolver la relación entre los dos, y es algo sorprendente. Por ejemplo, Johnson (2013) presenta un caso bastante convincente de que (al menos para las pruebas t) el umbral p < .05 corresponde aproximadamente a un factor de Bayes de entre 3:1 y 5:1 a favor de la alternativa. Si eso es correcto, entonces la afirmación de Fisher es un poco exagerada. Supongamos que la hipótesis nula es cierta aproximadamente la mitad de las veces (es decir, la probabilidad previa de \(H_0\) es 0,5), y usamos esos números para calcular la probabilidad posterior de la hipótesis nula dado que ha sido rechazada en p < .05. Utilizando los datos de Johnson (2013), vemos que si rechaza el valor nulo en p ă .05, estará en lo correcto aproximadamente el 80 % de las veces. No sé usted, pero, en mi opinión, un estándar probatorio que le asegure que se equivocará en el 20 % de sus decisiones no es suficiente. El hecho es que, contrariamente a la afirmación de Fisher, si rechaza en p < 0,05, muy a menudo se equivocará. No es un umbral probatorio muy estricto en absoluto.
16.3.3 El valor p es una mentira.
El pastel es mentira.
El pastel es mentira.
El pastel es mentira.
El pastel es mentira.
– Portal11
Bien, en este punto podrías estar pensando que el verdadero problema no es con las estadísticas ortodoxas, sino con el estándar p < .05. En cierto sentido, eso es cierto. La recomendación que da Johnson (2013) no es que “todos deben ser bayesianos ahora”. En cambio, la sugerencia es que sería más inteligente cambiar el estándar convencional a algo así como un nivel de p < .01. Esa no es una opinión irrazonable, pero en mi opinión, el problema es un poco más grave que eso. En mi opinión, hay un problema bastante grande en la forma en que se construyen la mayoría (pero no todas) las pruebas de hipótesis ortodoxas. Son groseramente ingenuos acerca de cómo los humanos realmente investigan y, debido a esto, la mayoría de los valores de p están equivocados.
Suena como una afirmación absurda, ¿verdad? Bueno, considere el siguiente escenario. Se le ocurrió una hipótesis de investigación realmente emocionante y diseñó un estudio para probarla. Eres muy diligente, así que ejecutas un análisis de potencia para determinar cuál debería ser el tamaño de la muestra y ejecutas el estudio. Ejecutas tu prueba de hipótesis y obtienes un valor p de 0.072. Realmente jodidamente molesto, ¿verdad?
¿Qué debes hacer? Aquí hay algunas posibilidades:
- Concluyes que no hay efecto e intentas publicarlo como resultado nulo
- Supone que podría haber un efecto e intenta publicarlo como un resultado “en el límite significativo”
- Te rindes e intentas un nuevo estudio
- Reúne algunos datos más para ver si el valor p sube o (¡preferiblemente!) cae por debajo del criterio “mágico” de p < .05
¿Cuál escogerías? Antes de seguir leyendo, le insto a que se tome un tiempo para pensarlo. Se honesto contigo mismo. Pero no te preocupes demasiado por eso, porque estás jodido sin importar lo que elijas. Basado en mis propias experiencias como autor, revisor y editor, así como en las historias que escuché de otros, esto es lo que sucederá en cada caso:
Comencemos con la opción 1. Si intenta publicarlo como un resultado nulo, el artículo tendrá dificultades para publicarse. Algunos revisores pensarán que p = .072 no es realmente un resultado nulo. Argumentarán que está en el límite significativo. Otros revisores estarán de acuerdo en que es un resultado nulo, pero afirmarán que, aunque algunos resultados nulos son publicables, el suyo no lo es. Uno o dos revisores podrían incluso estar de su lado, pero tendrá que luchar una batalla cuesta arriba para lograrlo.
Bien, pensemos en la opción número 2. Supongamos que intenta publicarlo como un resultado límite significativo. Algunos revisores afirmarán que es un resultado nulo y que no debería publicarse. Otros afirmarán que la evidencia es ambigua y que debe recopilar más datos hasta que obtenga un resultado claro y significativo. Una vez más, el proceso de publicación no le favorece.
Dadas las dificultades para publicar un resultado “ambiguo” como p = .072, la opción número 3 puede parecer tentadora: rendirse y hacer otra cosa. Pero esa es una receta para el suicidio profesional. Si te rindes y pruebas un nuevo proyecto cada vez que te enfrentas a la ambigüedad, tu trabajo nunca se publicará. Y si estás en la academia sin un registro de publicación puedes perder tu trabajo. Así que esa opción está descartada.
Parece que está atascado con la opción 4. No tiene resultados concluyentes, por lo que decide recopilar más datos y volver a ejecutar el análisis. Parece sensato, pero desafortunadamente para usted, si hace esto, todos sus valores p ahora son incorrectos. Todos ellos. No solo los valores p que calculó para este estudio. Todos ellos. Todos los valores p que calculó en el pasado y todos los valores p que calculará en el futuro. Afortunadamente, nadie se dará cuenta. Te publicarán y habrás mentido.
¿Esperar lo? ¿Cómo puede ser cierta esa última parte? Quiero decir, suena como una estrategia perfectamente razonable, ¿no? Recolectó algunos datos, los resultados no fueron concluyentes, por lo que ahora lo que desea hacer es recopilar más datos hasta que los resultados sean concluyentes. ¿Qué está mal con eso?
Honestamente, no hay nada de malo en ello. Es algo razonable, sensato y racional. En la vida real, esto es exactamente lo que hace todo investigador. Desafortunadamente, la teoría de nula [Prueba de hipótesis] como la describí en un capítulo anterior le prohíbe hacer esto.12 La razón es que la teoría asume que el experimento ha terminado y todos los datos están in. Y debido a que asume que el experimento ha terminado, solo considera dos decisiones posibles. Si usa el umbral convencional p < .05, esas decisiones se muestran en Table 16.11.
| Outcome | Action |
|---|---|
| p less than .05 | Reject the null |
| p greater than .05 | Retain the null |
Lo que estás haciendo es agregar una tercera acción posible al problema de toma de decisiones. Específicamente, lo que estás haciendo es usar el valor p como una razón para justificar continuar con el experimento. Y como consecuencia, ha transformado el procedimiento de toma de decisiones en uno que se parece más a Table 16.12.
| Outcome | Action |
|---|---|
| p less than .05 | Stop the experiment and reject the null |
| p between .05 and .1 | Continue the experiment |
| p greater than .1 | Stop the experiment and retain the null |
La teoría “básica” de nula [prueba de hipótesis] no está construida para manejar este tipo de cosas, no en la forma que describí en ese capítulo anterior. Si usted es el tipo de persona que elegiría “recolectar más datos” en la vida real, eso implica que no está tomando decisiones de acuerdo con las reglas de la prueba de hipótesis nula. Incluso si llega a la misma decisión que la prueba de hipótesis, no está siguiendo el proceso de decisión que implica, y es esta falla en seguir el proceso lo que está causando el problema.13 Su p -Los valores son una mentira.
Peor aún, son una mentira de una manera peligrosa, porque todos son demasiado pequeños. Para darle una idea de lo malo que puede ser, considere el siguiente escenario (en el peor de los casos). Imagina que eres un investigador súper entusiasta con un presupuesto ajustado que no prestó atención a mis advertencias anteriores. Usted diseña un estudio comparando dos grupos. Desea desesperadamente ver un resultado significativo en el nivel \(p < .05\), pero realmente no desea recopilar más datos de los necesarios (porque es costoso). Para reducir los costos, comienza a recopilar datos, pero cada vez que llega un conjunto de observaciones, ejecuta una prueba t en sus datos. Si la prueba t dice \(p < .05\), detiene el experimento e informa un resultado significativo. Si no, sigue recopilando datos. Siga haciendo esto hasta que alcance su límite de gasto predefinido para este experimento. Digamos que el límite se activa en \(N = 1000\) observaciones. Como resultado, la verdad del asunto es que no se puede encontrar ningún efecto real: la hipótesis nula es verdadera. Entonces, ¿cuál es la probabilidad de que llegues al final del experimento y (correctamente) concluyas que no hay efecto? En un mundo ideal, la respuesta aquí debería ser 95%. Después de todo, el punto central del criterio \(p < .05\) es controlar la tasa de error Tipo I al 5 %, por lo que lo que esperamos es que solo haya un 5 % de posibilidades de rechazar falsamente la hipótesis nula en esta situación. . Sin embargo, no hay garantía de que eso sea cierto. Estás rompiendo las reglas. Debido a que está ejecutando pruebas repetidamente, “echando un vistazo” a sus datos para ver si ha obtenido un resultado significativo, todas las apuestas están canceladas.
Entonces, ¿qué tan malo es? La respuesta se muestra como una línea sólida en Figure 16.1, y es asombrosamente mala. Si echa un vistazo a sus datos después de cada observación, hay un 53% de posibilidades de que cometa un error de tipo I. Eso es, um, un poco más grande que el 5% que se supone que es. Y no mejora mucho con un vistazo menos frecuente: si solo miras cada 10 o cada 50 observaciones. entonces las tasas de error de Tipo I siguen siendo demasiado altas: 38% y 29%, respectivamente. A modo de comparación, imagine que ha utilizado la siguiente estrategia. Comience a recopilar datos. Cada vez que llegue una observación, ejecute pruebas t bayesianas y mire el factor de Bayes. Asumiré que Johnson (2013) tiene razón, y trataré un factor de Bayes de 3:1 como aproximadamente equivalente a un valor p de .05.14 Esta vez, nuestro investigador de gatillo feliz utiliza el siguiente procedimiento. Si el factor de Bayes es 3:1 o más a favor del nulo, detenga el experimento y conserve el nulo. Si es 3:1 o más a favor de la alternativa, detenga el experimento y rechace el nulo. De lo contrario, continúe probando. Ahora, como la última vez, supongamos que la hipótesis nula es verdadera. ¿Lo que sucede? Da la casualidad de que también ejecuté las simulaciones para este escenario y los resultados se muestran como la línea discontinua en @ fig-fig16-1. Resulta que la tasa de error de Tipo I para echar un vistazo cada vez que llega una nueva observación es del 24%, mucho más baja que la tasa del 53% que obtuvimos al usar la prueba t ortodoxa. Y para asomarse cada 10 o 50 observaciones las tasas son del 11% y 8%, respectivamente.

En cierto modo, esto es notable. Todo el punto de la prueba de hipótesis nula ortodoxa es controlar la tasa de error Tipo I. Los métodos bayesianos en realidad no están diseñados para hacer esto en absoluto. Sin embargo, resulta que cuando se enfrenta a un investigador de “gatillo feliz” que continúa realizando pruebas de hipótesis a medida que ingresan los datos, el enfoque bayesiano es mucho más efectivo. Incluso el estándar 3:1, que la mayoría de los bayesianos consideraría inaceptablemente laxo, es mucho más seguro que la regla p < 0,05.
16.3.4 ¿Es realmente tan malo?
El ejemplo que di en la sección anterior es una situación bastante extrema. En la vida real, las personas no realizan pruebas de hipótesis cada vez que llega una nueva observación. Por lo tanto, no es justo decir que el umbral p < .05 “realmente” corresponde a una tasa de error Tipo I del 53% (es decir, p = 0.53). Pero el hecho es que si desea que sus valores p sean honestos, debe cambiar a una forma completamente diferente de hacer pruebas de hipótesis o aplicar una regla estricta de no mirar a escondidas. No se le permite utilizar los datos para decidir cuándo finalizar el experimento. No se le permite mirar un valor p “límite” y decidir recopilar más datos. Ni siquiera se le permite cambiar su estrategia de análisis de datos después de mirar los datos. Está estrictamente obligado a seguir estas reglas, de lo contrario, los valores p que calcule no tendrán sentido.
Y sí, estas reglas son sorprendentemente estrictas. Como ejercicio de clase hace un par de años, les pedí a los estudiantes que pensaran en este escenario. Suponga que comenzó a realizar su estudio con la intención de reunir \(N = 80\) personas. Cuando comienza el estudio, sigues las reglas y te niegas a mirar los datos o realizar cualquier prueba. Pero cuando llegas a \(N = 50\) tu fuerza de voluntad cede… y echas un vistazo. ¿Adivina qué? ¡Tienes un resultado significativo! Ahora, claro, sabes que dijiste que seguirías realizando el estudio con un tamaño de muestra de \(N = 80\), pero parece un poco inútil ahora, ¿verdad? El resultado es significativo con un tamaño de muestra de \(N = 50\), entonces, ¿no sería un desperdicio e ineficiente seguir recopilando datos? ¿No estás tentado a parar? ¿Solo un poco? Bueno, tenga en cuenta que si lo hace, su tasa de error de Tipo I en \(p < .05\) simplemente se disparó al 8%. Cuando reporta \(p < .05\) en su trabajo, lo que realmente está diciendo es \(p < .08\). Así de malas pueden ser las consecuencias de “solo un vistazo”.
Ahora considera esto. La literatura científica está llena de pruebas t, ANOVA, regresiones y pruebas de chi-cuadrado. Cuando escribí este libro no elegí estas pruebas arbitrariamente. La razón por la que estas cuatro herramientas aparecen en la mayoría de los textos de introducción a la estadística es que son las herramientas básicas de la ciencia. Ninguna de estas herramientas incluye una corrección para lidiar con el “vistazo de datos”: todas asumen que no lo estás haciendo. Pero, ¿qué tan realista es esa suposición? En la vida real, ¿cuántas personas cree que “miraron” sus datos antes de que terminara el experimento y adaptaron su comportamiento posterior después de ver cómo se veían los datos? Excepto cuando el procedimiento de muestreo está fijado por una restricción externa, supongo que la respuesta es “la mayoría de la gente lo ha hecho”. Si eso ha sucedido, puede inferir que los valores p informados son incorrectos. Peor aún, debido a que no sabemos qué proceso de decisión siguieron en realidad, no tenemos forma de saber cuáles deberían haber sido los valores p. No puede calcular un valor p cuando no conoce el procedimiento de toma de decisiones que utilizó el investigador. Y así, el valor p informado sigue siendo una mentira.
Teniendo en cuenta todo lo anterior, ¿cuál es el mensaje para llevar a casa? No es que los métodos bayesianos sean infalibles. Si un investigador está decidido a hacer trampa, siempre puede hacerlo. La regla de Bayes no puede impedir que la gente mienta, ni puede impedir que manipulen un experimento. Ese no es mi punto aquí. Mi punto es el mismo que planteé al comienzo del libro en la Sección 1.1: la razón por la que realizamos pruebas estadísticas es para protegernos de nosotros mismos. Y la razón por la que “mirar a escondidas los datos” es tan preocupante es que es muy tentador, incluso para los investigadores honestos. Una teoría para la inferencia estadística tiene que reconocer esto. Sí, podría tratar de defender los valores de p diciendo que es culpa del investigador por no usarlos correctamente, pero en mi opinión, eso no entiende el punto. Una teoría de la inferencia estadística que es tan completamente ingenua acerca de los humanos que ni siquiera considera la posibilidad de que el investigador pueda ver sus propios datos no es una teoría que valga la pena tener. En esencia, mi punto es este:
Las buenas leyes tienen su origen en la mala moral.
– Ambrosius Macrobius 15
Las buenas reglas para las pruebas estadísticas deben reconocer la fragilidad humana. Ninguno de nosotros está libre de pecado. Ninguno de nosotros está más allá de la tentación. Un buen sistema de inferencia estadística debería funcionar incluso cuando lo utilizan seres humanos reales. La prueba de hipótesis nula ortodoxa no lo hace.16
16.4 Pruebas t bayesianas
Un tipo importante de problema de inferencia estadística discutido en este libro es [Comparación de dos medias], discutido con cierto detalle en el capítulo sobre pruebas t. Si puede recordar ese momento, recordará que hay varias versiones de la prueba t. Hablaré un poco sobre las versiones bayesianas de las pruebas t de muestras independientes y la prueba t de muestras pareadas en esta sección.
16.4.1 Prueba t de muestras independientes
El tipo más común de prueba t es la prueba t de muestras independientes, y surge cuando tiene datos como en el conjunto de datos harpo.csv que usamos en Chapter 11 en pruebas t. En este conjunto de datos, tenemos dos grupos de estudiantes, los que recibieron lecciones de Anastasia y los que tomaron sus clases con Bernadette. La pregunta que queremos responder es si hay alguna diferencia en las calificaciones que reciben estos dos grupos de estudiantes. En ese [capítulo] (Comparación de dos medias) sugerí que podría analizar este tipo de datos utilizando la prueba t de muestras independientes en jamovi, que nos dio los resultados en Figure 16.2. Como obtenemos un p-valor inferior a 0,05, rechazamos la hipótesis nula.
¿Cómo es la versión bayesiana de la prueba t? Podemos obtener el análisis del factor de Bayes seleccionando la casilla de verificación ‘Factor de Bayes’ en la opción ‘Pruebas’ y aceptando el valor predeterminado sugerido para el ‘Previo’. Esto da los resultados que se muestran en la tabla en Figure 16.3. Lo que obtenemos en esta tabla es un factor estadístico de Bayes de 1,75, lo que significa que la evidencia proporcionada por estos datos es de aproximadamente 1,8:1 a favor de la hipótesis alternativa.
Antes de continuar, vale la pena resaltar la diferencia entre los resultados de la prueba ortodoxa y la bayesiana. Según la prueba ortodoxa, obtuvimos un resultado significativo, aunque apenas. Sin embargo, mucha gente aceptaría felizmente p = .043 como evidencia razonablemente sólida de un efecto. Por el contrario, tenga en cuenta que la prueba bayesiana ni siquiera alcanza una probabilidad de 2:1 a favor de un efecto y, en el mejor de los casos, se consideraría una evidencia muy débil. En mi experiencia, ese es un resultado bastante típico. Los métodos bayesianos generalmente requieren más evidencia antes de rechazar el valor nulo.

16.4.2 Prueba t de muestras pareadas
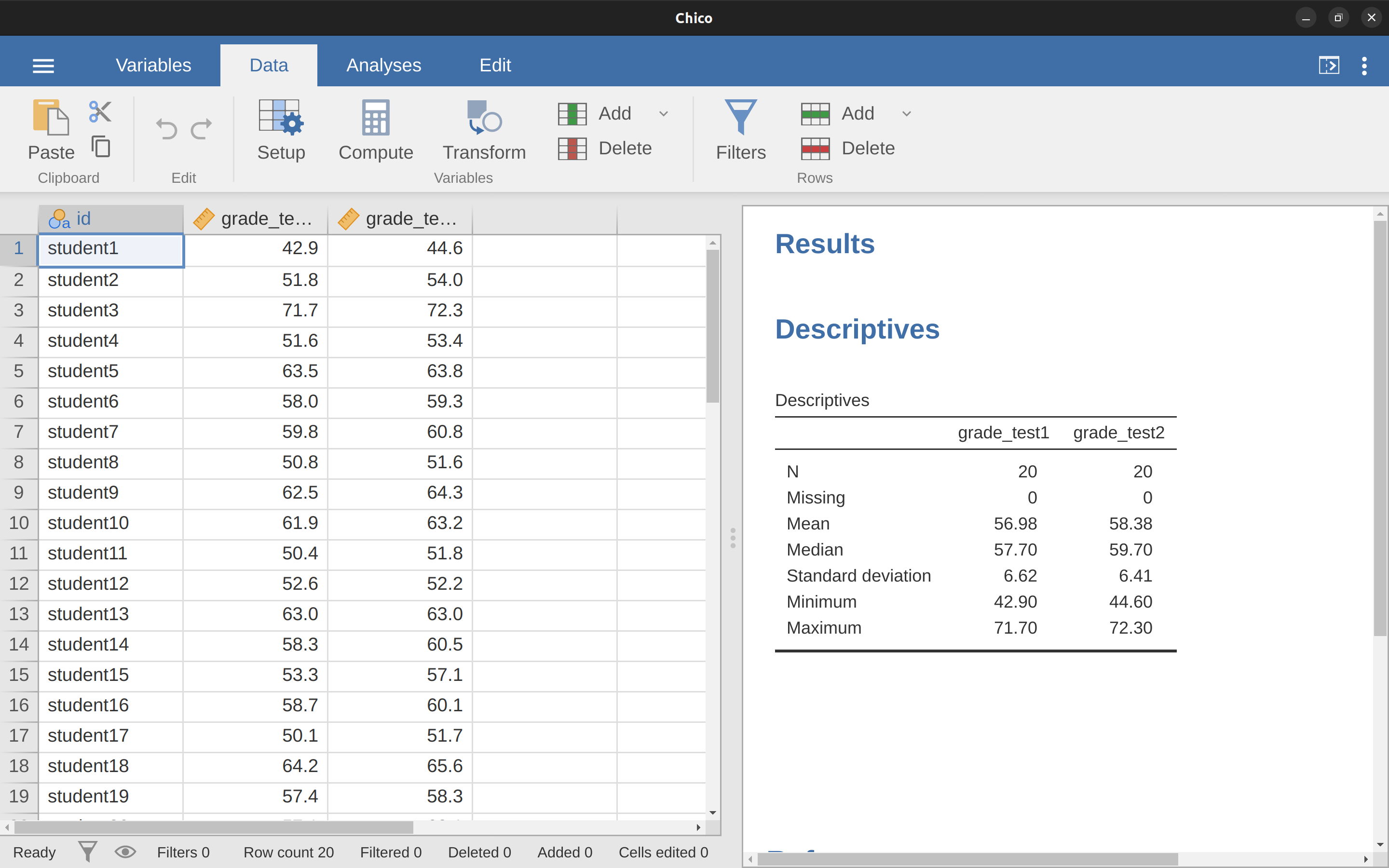
En la Sección 11.5, analicé el conjunto de datos chico.csv en el que las calificaciones de los estudiantes se midieron en dos pruebas, y estábamos interesados en saber si las calificaciones aumentaron de la prueba 1 a la prueba 2. Debido a que cada estudiante hizo ambas pruebas, la herramienta que usamos utilizado para analizar los datos fue una prueba t de muestras pareadas. Figure 16.4 muestra la tabla de resultados jamovi para la prueba t pareada convencional junto con el análisis factorial de Bayes. En este punto, espero que puedas leer este resultado sin ninguna dificultad. Los datos proporcionan evidencia de alrededor de 6000:1 a favor de la alternativa. ¡Probablemente podríamos rechazar el nulo con cierta confianza!

16.5 Resumen
La primera mitad de este capítulo se centró principalmente en los fundamentos teóricos de las estadísticas bayesianas. Presenté las matemáticas de cómo funciona la inferencia bayesiana en la sección sobre Razonamiento probabilístico por agentes racionales, y brindé una descripción general muy básica de las pruebas de hipótesis bayesianas]. Finalmente, dediqué algo de espacio a hablar sobre por qué creo que [vale la pena usar los métodos bayesianos] (¿Por qué ser bayesiano?).
Luego di un ejemplo práctico, con pruebas t bayesianas. Si está interesado en aprender más sobre el enfoque bayesiano, hay muchos buenos libros que podría consultar. El libro de John Kruschke Doing Bayesian Data Analysis es un muy buen lugar para comenzar (Kruschke, 2011) y es una buena combinación de teoría y práctica. Su enfoque es un poco diferente al enfoque del “factor de Bayes” que he discutido aquí, por lo que no cubrirá el mismo terreno. Si es psicólogo cognitivo, puede consultar Lee & Wagenmakers (2014). Elegí estos dos porque creo que son especialmente útiles para las personas en mi disciplina, pero hay muchos libros buenos, ¡así que mira a tu alrededor!
<a href=“http://en.wikiquote.org/wiki/David%20Hume”. target=“_blank”>http://en.wikiquote.org/wiki/David_Hume.↩︎
Es un acto de fe, lo sé, pero sigamos adelante, ¿de acuerdo?↩︎
Um. Odio mencionar esto, pero algunos estadísticos se opondrían a que use la palabra “probabilidad” aquí. El problema es que la palabra “probabilidad” tiene un significado muy específico en las estadísticas frecuentistas, y no es lo mismo que lo que significa en las estadísticas bayesianas. Por lo que puedo decir, los bayesianos originalmente no tenían un nombre acordado para la probabilidad, por lo que se convirtió en una práctica común para las personas usar la terminología frecuentista. Esto no habría sido un problema excepto por el hecho de que la forma en que los bayesianos usan la palabra resulta ser bastante diferente a la forma en que lo hacen los frecuentistas. Este no es el lugar para otra larga lección de historia pero, para decirlo crudamente, cuando un bayesiano dice “una función de probabilidad” por lo general se refiere a una de las filas de la tabla. Cuando un frecuentador dice lo mismo, se refiere a la misma tabla, pero para ellos “una función de probabilidad” casi siempre se refiere a una de las columnas. Esta distinción es importante en algunos contextos, pero no es importante para nuestros propósitos.↩︎
Para ser claros, la información “previa” es conocimiento o creencias preexistentes, antes de que recopilemos o usemos cualquier dato para mejorar esa información.↩︎
si fuéramos un poco más sofisticados, podríamos extender el ejemplo para acomodar la posibilidad de que esté mintiendo sobre el paraguas. Pero mantengamos las cosas simples, ¿de acuerdo?↩︎
puede notar que esta ecuación es en realidad una reafirmación de la misma regla básica que enumeré al comienzo de la última sección. Si multiplica ambos lados de la ecuación por \(P(d)\), obtiene \(P(d)P(h|d) = P(d, h)\), que es la regla para calcular las probabilidades conjuntas. Así que en realidad no estoy introduciendo ninguna regla “nueva” aquí, solo estoy usando la misma regla de una manera diferente.↩︎
Obviamente, esta es una historia muy simplificada. Toda la complejidad de las pruebas de hipótesis bayesianas de la vida real se reduce a cómo se calcula la probabilidad \(P(d\|h)\) cuando la hipótesis h es algo complejo y vago. No voy a hablar sobre esas complejidades en este libro, pero sí quiero resaltar que, aunque esta simple historia es cierta hasta donde llega, la vida real es más complicada de lo que puedo cubrir en un libro de texto de introducción a las estadísticas.↩︎
http://www.imdb.com/title/tt0093779/quotes . Debo señalar de paso que no soy la primera persona que usa esta cita para quejarse de los métodos frecuentadores. Rich Morey y sus colegas tuvieron la idea primero. Lo estoy robando descaradamente porque es una cita increíble para usar en este contexto y me niego a perder cualquier oportunidad de citar La princesa prometida.↩︎
http ://about.abc.net.au/reports-publications/appreciation-survey-summary-report-2013/↩︎
Para ser completamente honesto, debo reconocer que no todas las pruebas estadísticas ortodoxas se basan en esta suposición tonta. Hay una serie de herramientas de análisis secuencial que a veces se utilizan en ensayos clínicos y similares. Estos métodos se basan en el supuesto de que los datos se analizan a medida que llegan, y estas pruebas no se rompen terriblemente en la forma en que me quejo aquí. Sin embargo, los métodos de análisis secuencial se construyen de una manera muy diferente a la versión “estándar” de la prueba de hipótesis nula. No se incluyen en ningún libro de texto introductorio y no se utilizan mucho en la literatura psicológica. La preocupación que planteo aquí es válida para todas las pruebas ortodoxas que he presentado hasta ahora y para casi todas las pruebas que he visto reportadas en los artículos que leí.↩︎
un problema relacionado: http://xkcd.com/1478/ .↩︎
Algunos lectores podrían preguntarse por qué elegí 3:1 en lugar de 5:1, dado que Johnson (2013) sugiere que \(p = 0,05\) se encuentra en algún lugar de ese rango. Lo hice para ser caritativo con el valor p. Si hubiera elegido un factor Bayesiano de 5:1, los resultados se verían incluso mejor para el enfoque bayesiano.↩︎
http://www.quotationspage.com/quotes/Ambrosius%20Macrobius/</a↩︎
De acuerdo, solo sé que algunos frecuentadores informados leerán esto y comenzarán a quejarse de esta sección. Mira, no soy tonto. Sé absolutamente que si adopta una perspectiva de análisis secuencial puede evitar estos errores dentro del marco ortodoxo. También sé que puede diseñar estudios explícitamente con análisis intermedios en mente. Así que sí, en cierto sentido estoy atacando una versión de “hombre de paja” de los métodos ortodoxos. Sin embargo, el hombre de paja que estoy atacando es el que usan casi todos los practicantes. Si alguna vez llega al punto en que los métodos secuenciales se convierten en la norma entre los psicólogos experimentales y ya no estoy obligado a leer 20 ANOVA extremadamente dudosos al día, prometo que reescribiré esta sección y reduciré el vitriolo. Pero hasta que llegue ese día, mantendré mi afirmación de que los métodos predeterminados del factor de Bayes son mucho más sólidos frente a las prácticas de análisis de datos que existen en el mundo real. Los métodos ortodoxos predeterminados apestan, y todos lo sabemos.↩︎