8  Estimación de cantidades desconocidas de una muestra

Al principio del último capítulo destaqué la distinción fundamental entre estadística descriptiva y estadística inferencial. Como se explica en Chapter 4, la función de la estadística descriptiva es resumir de manera concisa lo que sabemos. Por el contrario, el propósito de la estadística inferencial es “aprender lo que no sabemos a partir de lo que sabemos”. Ahora que tenemos una base en la teoría de la probabilidad, estamos en una buena posición para pensar en el problema de la inferencia estadística. ¿Qué tipo de cosas nos gustaría aprender? ¿Y cómo las aprendemos? Estas son las preguntas que constituyen el nucleo de la estadística inferencial, y tradicionalmente se dividen en dos “grandes ideas”: estimación y prueba de hipótesis. El objetivo de este capítulo es presentar la primera de estas grandes ideas, la teoría de la estimación, pero primero hablaré sobre la teoría del muestreo porque la teoría de la estimación no tiene sentido hasta que se entiende el muestreo. Como consecuencia, este capítulo se divide naturalmente en dos partes: las tres primeras secciones se centran en la teoría del muestreo y las dos últimas secciones hacen uso de la teoría del muestreo para discutir cómo piensan los estadísticos acerca de la estimación.

8.1 Muestras, poblaciones y muestreo

En el preludio de la parte IV, hablé del enigma de la inducción y destaqué el hecho de que todo aprendizaje requiere hacer suposiciones. Aceptando que esto es cierto, nuestra primera tarea consiste en plantear algunas hipótesis bastante generales sobre los datos que tengan sentido. Aquí es donde entra en juego la teoría del muestreo. Si la teoría de la probabilidad es la base sobre la que se construye toda la teoría estadística, la teoría del muestreo es el marco alrededor del cual se puede construir el resto de la casa. La teoría del muestreo juega un papel fundamental a la hora de especificar los supuestos en los que se basan las inferencias estadísticas. Y para hablar de “hacer inferencias” de la forma en que los estadísticos piensan en ello, debemos ser un poco más explícitas acerca de lo que estamos haciendo inferencias a partir de (la muestra) y sobre lo que estamos haciendo inferencias (la población).

En casi todas las situaciones de interés, lo que tenemos a nuestra disposición como investigadoras es una muestra de datos. Podríamos haber realizado un experimento con un número determinado de participantes, una empresa de sondeos podría haber llamado por teléfono a un número determinado de personas para preguntarles sobre las intenciones de voto, etc. De esta forma, el conjunto de datos de que disponemos es finito e incompleto. Es imposible que todas las personas del mundo participen en nuestro experimento; por ejemplo, una empresa de sondeos no tiene el tiempo ni el dinero para llamar a todos los votantes del país. En nuestro debate anterior sobre estadística descriptiva en Chapter 4, esta muestra era lo único que nos interesaba. Nuestro único objetivo era encontrar formas de describir, resumir y representar gráficamente esa muestra. Esto está a punto de cambiar.

8.1.1 Definir una población

Una muestra es algo concreto. Puede abrir un archivo de datos y allí están los datos de tu muestra. Una población, en cambio, es una idea más abstracta. Se refiere al conjunto de todas las personas posibles, o todas las observaciones posibles, sobre las que se quieren sacar conclusiones y, por lo general, es mucho más grande que la muestra. En un mundo ideal, el investigador comenzaría el estudio con una idea clara de cuál es la población de interés, ya que el proceso de diseñar un estudio y probar hipótesis con los datos depende de la población sobre la que se quiere hacer afirmaciones.

A veces es fácil establecer la población de interés. Por ejemplo, en el ejemplo de la “empresa de sondeos” que abrió el capítulo, la población estaba compuesta por todos los votantes inscritos en el momento del estudio, millones de personas. La muestra era un conjunto de 1000 personas que pertenecientes todas ellas a dicha población. En la mayoría de los estudios, la situación es mucho menos sencilla. En un experimento psicológico típico, determinar la población de interés es un poco más complicado. Supongamos que realizo un experimento con 100 estudiantes universitarios como participantes. Mi objetivo, como científica cognitiva, es intentar aprender algo sobre el funcionamiento de la mente. Entonces, ¿cuál de los siguientes contaría como “la población”?

• ¿Todos los estudiantes de psicología de la Universidad de Adelaida?
• ¿Los estudiantes de psicología en general, de cualquier parte del mundo?
• ¿Australianos que viven actualmente?
• ¿Australianos de edades similares a las de mi muestra?
• ¿Cualquier persona viva en la actualidad?
• ¿Cualquier ser humano, pasado, presente o futuro?
• ¿Cualquier organismo biológico con un grado de inteligencia suficiente que opere en un medio terrestre?
• ¿Cualquier ser inteligente?

Cada una de ellas define un grupo real de entidades poseedoras de mente, todas las cuales podrían interesarme como científica cognitiva, y no está nada claro cuál debería ser la verdadera población de interés. Como otro ejemplo, consideremos el juego Wellesley-Croker que discutimos en el Preludio de la parte IV. La muestra aquí es una secuencia específica de 12 victorias y 0 derrotas para Wellesley. ¿Cual es la población? De nuevo, no es obvio cuál es la población.

• ¿Todos los resultados hasta que Wellesley y Croker llegaron a su destino?
• ¿Todos los resultados si Wellesley y Croker hubieran jugado al juego durante el resto de sus vidas?
• ¿Todos los resultados si Wellseley y Croker vivieran para siempre y jugaran al juego hasta que el mundo se quedara sin colinas?
• ¿Todos los resultados si creáramos un conjunto infinito de universos paralelos y la pareja Wellesely/Croker adivinara las mismas 12 colinas en cada universo?

8.1.2 Muestras aleatorias simples

Independientemente de cómo definas la población, el punto crítico es que la muestra es un subconjunto de la población y nuestro objetivo es utilizar nuestro conocimiento de la muestra para hacer inferencias sobre las propiedades de la población. La relación entre ambos depende del procedimiento por el que se seleccionó la muestra. Este procedimiento se denomina método de muestreo y es importante entender por qué es importante.

Para simplificar, imaginemos que tenemos una bolsa con 10 fichas. Cada ficha lleva impresa una letra única para que podamos distinguir las 10 fichas. Las fichas son de dos colores, blanco y negro. Este conjunto de fichas es la población de interés y se representa gráficamente a la izquierda de Figure 8.1. Como puedes ver en la imagen, hay 4 fichas negras y 6 blancas, pero en la vida real no lo sabríamos a menos que miráramos en la bolsa. Ahora imagina que haces el siguiente “experimento”: agitas la bolsa, cierras los ojos y sacas 4 fichas sin volver a meter ninguna en la bolsa. Primero sale la ficha a (negra), luego la c (blanca), después la j (blanca) y finalmente la b (negra). Si quisieras, podrías volver a meter todas las fichas en la bolsa y repetir el experimento, como se muestra en el lado derecho de Figure 8.1. Cada vez se obtienen resultados diferentes, pero el procedimiento es idéntico en todos los casos. El hecho de que el mismo procedimiento pueda llevar a resultados diferentes cada vez lo denominamos proceso aleatorio.¹ Sin embargo, como agitamos la bolsa antes de sacar ninguna ficha, parece razonable pensar que todas las fichas tienen la misma probabilidad de ser seleccionadas. Un procedimiento en el que cada miembro de la población tiene la misma probabilidad de ser seleccionado se denomina muestra aleatoria simple. El hecho de que no hayamos vuelto a meter las fichas en la bolsa después de sacarlas significa que no se puede observar lo mismo dos veces y, en tales casos, se dice que las observaciones se han muestreado sin reemplazo.

Figure 8.1: muestreo aleatorio simple sin reemplazo de una población finita

Para asegurarte de que comprendes la importancia del procedimiento de muestreo, considera una forma alternativa en la que podría haberse realizado el experimento. Supongamos que mi hijo de 5 años hubiera abierto la bolsa y decidido sacar cuatro fichas negras sin volver a meter ninguna en la bolsa. Este esquema de muestreo sesgado se representa en Figure 8.2. Consideremos ahora el valor probatorio de ver 4 fichas negras y 0 blancas. Está claro que depende del esquema de muestreo, ¿no? Si sabemos que el sistema de muestreo está sesgado para seleccionar solo fichas negras, entonces una muestra compuesta solo por fichas negras no nos dice mucho sobre la población. Por esta razón, a los estadísticos les gusta mucho cuando un conjunto de datos puede considerarse una muestra aleatoria simple, porque facilita mucho el análisis de datos.

Figure 8.2: Muestreo sesgado sin reemplazo de una población finita

Merece la pena mencionar un tercer procedimiento. Esta vez cerramos los ojos, agitamos la bolsa y sacamos una ficha. Esta vez, sin embargo, anotamos la observación y luego volvemos a meter la ficha en la bolsa. Volvemos a cerrar los ojos, agitamos la bolsa y sacamos una ficha. Repetimos este procedimiento hasta tener 4 fichas. Los conjuntos de datos generados de esta forma siguen siendo muestras aleatorias simples, pero como volvemos a meter las fichas en la bolsa inmediatamente después de extraerlas, se denomina muestra con reemplazo. La diferencia entre esta situación y la primera es que es posible observar al mismo miembro de la población varias veces, como se ilustra en Figure 8.3.

Figure 8.3: Muestreo aleatorio simple con reemplazo de una población finita

Según mi experiencia, la mayoría de los experimentos de psicología suelen ser muestreos sin reemplazo, porque no se permite que la misma persona participe en el experimento dos veces. Sin embargo, la mayor parte de la teoría estadística se basa en el supuesto de que los datos proceden de una muestra aleatoria simple con reemplazo. En la vida real, esto rara vez importa. Si la población de interés es grande (por ejemplo, tiene más de 10 entidades), la diferencia entre el muestreo con y sin reemplazo es demasiado pequeña como para preocuparse por ella. En cambio, la diferencia entre muestras aleatorias simples y muestras sesgadas no es tan fácil de descartar.

8.1.3 La mayoría de las muestras no son muestras aleatorias simples

Como se puede ver en la lista de posibles poblaciones que he mostrado antes, es casi imposible obtener una muestra aleatoria simple de la mayoría de las poblaciones de interés. Cuando realizo experimentos, consideraría un pequeño milagro que mis participantes fueran una muestra aleatoria de los estudiantes de psicología de la Universidad de Adelaida, aunque esta es, con diferencia, la población más reducida a la que podría querer generalizar. Un análisis exhaustivo de otros tipos de sistemas de muestreo queda fuera del alcance de este libro, pero para que te hagas una idea de lo que hay, enumeraré algunos de los más importantes.

• Muestreo estratificado. Supongamos que tu población está (o puede estar) dividida en varias subpoblaciones o estratos diferentes. Por ejemplo, puede que estés realizando un estudio en varios sitios diferentes. En lugar de intentar obtener muestras aleatorias de la población en su conjunto, se intenta recoger una muestra aleatoria separada de cada uno de los estratos. El muestreo estratificado a veces es más fácil de realizar que el muestreo aleatorio simple, sobre todo cuando la población ya está dividida en estratos distintos. También puede ser más eficaz que el muestreo aleatorio simple, especialmente cuando algunas de las subpoblaciones son poco frecuentes. Por ejemplo, cuando se estudia la esquizofrenia, sería mucho mejor dividir la población en dos ² estratos (esquizofrénicos y no esquizofrénicos) y luego muestrear un número igual de personas de cada grupo. Si seleccionaras personas al azar, tendrías tan pocas personas esquizofrénicas en la muestra que tu estudio sería inútil. Este tipo específico de muestreo estratificado se conoce como sobremuestreo porque intenta deliberadamente sobrerrepresentar a grupos poco frecuentes.
• El muestreo de bola de nieve es una técnica especialmente útil cuando se toman muestras de una población “oculta” o de difícil acceso y es especialmente habitual en ciencias sociales. Por ejemplo, supongamos que los investigadores quieren realizar una encuesta de opinión entre personas transgénero. Es posible que el equipo de investigación solo disponga de los datos de contacto de unas pocas personas trans, por lo que la encuesta comienza pidiéndoles que participen (etapa 1). Al final de la encuesta, se pide a los participantes que faciliten los datos de contacto de otras personas que puedan querer participar. En la etapa 2 se encuesta a esos nuevos contactos. El proceso continúa hasta que los investigadores disponen de datos suficientes. La gran ventaja del muestreo de bola de nieve es que obtiene datos en situaciones que de otro modo serían imposibles de obtener. Desde el punto de vista estadístico, la principal desventaja es que la muestra es muy poco aleatoria, y poco aleatoria en aspectos difíciles de abordar. En la vida real, la desventaja es que el procedimiento puede ser poco ético si no se maneja bien, porque las poblaciones ocultas suelen estar oculatas por una razón. He elegido a las personas transgénero como ejemplo para destacar este problema. Si no se tiene cuidado, se puede acabar delatando a personas que no quieren ser delatadas (muy, muy mala forma), e incluso si no se comete ese error, puede resultar intrusivo usar las redes sociales de las personas para estudiarlas. Sin duda, es muy difícil obtener el consentimiento informado de las personas antes de ponerse en contacto con ellas, pero en muchos casos el simple hecho de ponerse en contacto con ellas y decirles “oye, queremos estudiarte” puede resultar hiriente. Las redes sociales son cosas complejas, y sólo porque puedas usarlas para obtener datos no siempre significa que debas hacerlo.
• Muestreo de conveniencia es más o menos lo que parece. Las muestras se eligen de forma que convenga a la investigadora y no se seleccionan al azar de la población de interés. El muestreo de bola de nieve es un tipo de muestreo de conveniencia, pero hay muchos otros. Un ejemplo común en psicología son los estudios que se basan en estudiantes universitarios de psicología. Estas muestras son generalmente no aleatorias en dos aspectos. En primer lugar, recurrir a estudiantes universitarios de psicología significa automáticamente que los datos se limitan a una única subpoblación. En segundo lugar, los estudiantes suelen elegir en qué estudios participarán, por lo que la muestra es un subconjunto de estudiantes de psicología autoseleccionados y no un subconjunto seleccionado al azar. En la vida real, la mayoría de los estudios son muestras de conveniencia de una forma u otra. Esto es a veces una limitación grave, pero no siempre.

8.1.4 ¿CQué importancia tiene no tener una muestra aleatoria simple?

De acuerdo, la recogida de datos en el mundo real no suele consistir en agradables muestras aleatorias simples. ¿Eso importa? Un poco de reflexión te dejará claro que puede importar si tus datos no son una muestra aleatoria simple. Piensa en la diferencia entre Figure 8.1 y Figure 8.2. Sin embargo, no es tan malo como parece. Algunos tipos de muestras sesgadas no plantean ningún problema. Por ejemplo, cuando utiliza una técnica de muestreo estratificado, realmente sabes cuál es el sesgo porque lo has creado deliberadamente, a menudo para aumentar la eficacia de tu estudio, y existen técnicas estadísticas que puedes utilizar para ajustar los sesgos que has introducido (no tratadas en este libro). Así que en esas situaciones no es un problema.

Sin embargo, en términos más generales, es importante recordar que el muestreo aleatorio es un medio para alcanzar un fin, y no el fin en sí mismo. Supongamos que has recurrido a una muestra de conveniencia y, como tal, puedes suponer que está sesgada. Un sesgo en tu método de muestreo es solo un problema si te lleva a sacar conclusiones equivocadas. Visto desde esa perspectiva, yo diría que no necesitamos que la muestra se genere aleatoriamente en todos los aspectos, solo necesitamos que sea aleatoria con respecto al fenómeno psicológicamente relevante de interés. Supongamos que estoy haciendo un estudio sobre la capacidad de memoria de trabajo. En el estudio 1, puedo tomar muestras aleatorias de todos los seres humanos vivos, con una excepción: solo puedo tomar muestras de personas nacidas un lunes. En el estudio 2, puedo tomar muestras al azar de la población australiana. Quiero generalizar mis resultados a la población de todos los seres humanos vivos. ¿Qué estudio es mejor? La respuesta, obviamente, es el estudio 1. ¿Por qué? Porque no tenemos ninguna razón para pensar que “nacer un lunes” tenga alguna relación interesante con la capacidad de la memoria de trabajo. En cambio, se me ocurren varias razones por las que “ser australiano” podría ser importante. Australia es un país rico e industrializado con un sistema educativo muy bien desarrollado. Las personas que crecen en ese sistema habrán tenido experiencias vitales mucho más parecidas a las de las personas que diseñaron las pruebas de capacidad de memoria de trabajo. Esta experiencia compartida podría traducirse fácilmente en creencias similares sobre cómo “hacer un examen”, una suposición compartida sobre cómo funciona la experimentación psicológica, etc. Estas cosas podrían ser realmente importantes. Por ejemplo, el estilo de “hacer exámenes” podría haber enseñado a los participantes australianos a dirigir su atención exclusivamente a materiales de examen bastante abstractos mucho más que a las personas que no han crecido en un entorno similar. Por tanto, esto podría dar lugar a una imagen engañosa de lo que es la capacidad de memoria de trabajo.

Hay dos puntos ocultos en esta discusión. En primer lugar, al diseñar tus propios estudios, es importante pensar en qué población te interesa y esforzarte por muestrear de forma adecuada esa población. En la práctica, una suele verse obligada a conformarse con una “muestra de conveniencia” (por ejemplo, los profesores de psicología recogen muestras de las estudiantes de psicología porque es la forma menos costosa de recopilar datos, y nuestras arcas no están precisamente rebosantes de oro), pero si es así una debería al menos dedicar algún tiempo a pensar cuáles pueden ser los peligros de esta práctica. En segundo lugar, si vas a criticar el estudio de otra persona porque ha utilizado una muestra de conveniencia en lugar de realizar un laborioso muestreo aleatorio de toda la población humana, al menos ten la cortesía de ofrecer una teoría específica sobre cómo esto podría haber distorsionado los resultados.

8.1.5 Parámetros poblacionales y estadísticas muestrales

Bueno. Dejando a un lado las espinosas cuestiones metodológicas asociadas a la obtención de una muestra aleatoria, consideremos una cuestión ligeramente diferente. Hasta ahora hemos hablado de poblaciones como lo haría un científico. Para una psicóloga, una población podría ser un grupo de personas. Para un ecologista, una población podría ser un grupo de osos. En la mayoría de los casos, las poblaciones que preocupan a los científicos son cosas concretas que existen en el mundo real. Los estadísticos, sin embargo, son un grupo curioso. Por un lado, les interesan los datos del mundo real y la ciencia real igual que a los científicos. Por otro lado, también operan en el ámbito de la abstracción pura, al igual que los matemáticos. En consecuencia, la teoría estadística tiende a ser un poco abstracta en cuanto a la definición de población. Del mismo modo que los investigadores psicológicos operacionalizan nuestras ideas teóricas abstractas en términos de mediciones concretas (Section 2.1), los estadísticos operacionalizan el concepto de “población” en términos de objetos matemáticos con los que saben trabajar. Estos objetos ya los hemos visto en Chapter 7. Se llaman distribuciones de probabilidad.

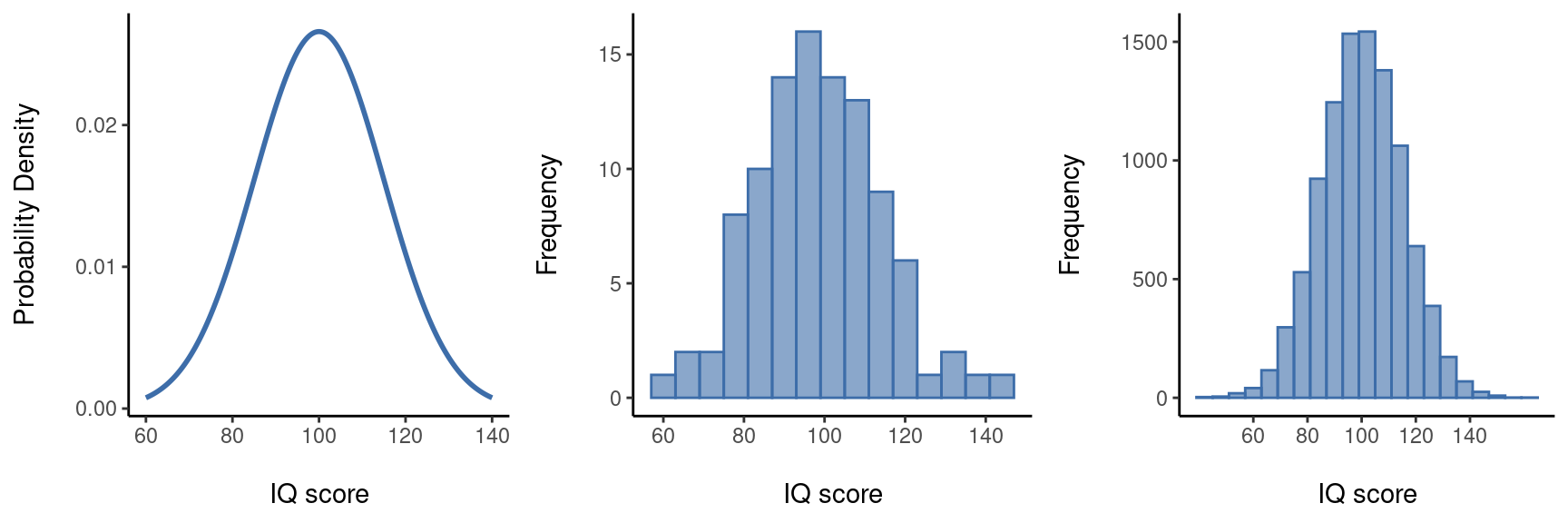
La idea es bastante sencilla. Digamos que estamos hablando de puntuaciones de CI. Para un psicólogo, la población de interés es un grupo de seres humanos reales que tienen puntuaciones de CI. Un estadístico “simplifica” esto definiendo operativamente la población como la distribución de probabilidad representada en Figure 8.4 (a). Las pruebas de CI están diseñadas para que el CI promedio sea 100, la desviación estándar de las puntuaciones de CI sea 15 y la distribución de las puntuaciones de CI sea normal. Estos valores se denominan parámetros poblacionales porque son características de toda la población. Es decir, decimos que la media poblacional µ es 100 y la desviación estándar poblacional σ es 15.

Figure 8.4: La distribución poblacional de puntuaciones de CI (panel (a)) y dos muestras extraídas al azar de ella. En el panel (b) tenemos una muestra de 100 observaciones, y en el panel (c) tenemos una muestra de 10,000 observaciones

Supongamos que hago un experimento. Selecciono 100 personas al azar y les administro una prueba de CI, lo que me da una muestra aleatoria simple de la población. Mi muestra consistiría en una colección de números como esta:

106 101 98 80 74 … 107 72 100

Cada una de estas puntuaciones de CI es una muestra de una distribución normal con media 100 y desviación estándar 15. Así que si trazo un histograma de la muestra, obtengo algo como lo que se muestra en Figure 8.4 (b). Como puedes ver, el histograma tiene aproximadamente la forma correcta, pero es una aproximación muy burda a la distribución real de la población que se muestra en Figure 8.4 (a). Cuando calculo la media de mi muestra, obtengo un número bastante cercano a la media poblacional 100, pero no idéntico. En este caso, resulta que las personas de mi muestra tienen una media de CI de 98,5 y la desviación estándar de sus puntuaciones de CI es 15,9. Estos estadísticos muestrales son propiedades de mi conjunto de datos y, aunque son bastante similares a los valores reales de la población, no son iguales. En general, los estadísticos muestrales son las cosas que puedes calcular a partir de tu conjunto de datos y los parámetros poblacionales son las cosas sobre las que quieres aprender. Más adelante en este capítulo hablaré de [Estimar los parámetros poblacionales] utilizando tus estadísticos muestrales y también de [Estimar un intervalo de confianza], pero antes de llegar a eso hay algunas ideas más sobre la teoría del muestreo que debes conocer.

8.2 La ley de los grandes números

En la sección anterior, te mostré los resultados de un experimento ficticio sobre el CI con un tamaño de muestra de N = 100. Los resultados fueron algo alentadores, ya que la media poblacional real es 100 y la media muestral de 98,5 es una aproximación bastante razonable. En muchos estudios científicos ese nivel de precisión es perfectamente aceptable, pero en otras situaciones necesitas ser mucho más precisa. Si queremos que los estadísticos muestrales se acerquen mucho más a los parámetros poblacionales, ¿qué podemos hacer? La respuesta obvia es recopilar más datos. Supongamos que realizamos un experimento mucho mayor, esta vez midiendo el CI de 10.000 personas. Podemos simular los resultados de este experimento usando jamovi. El archivo IQsim.omv es un archivo de datos de jamovi. En este archivo he generado 10,000 números aleatorios muestreados a partir de una distribución normal para una población con media = 100 y sd = 15. Esto se ha hecho calculando una nueva variable usando la función = NORM(100,15). Un histograma y un gráfico de densidad muestran que esta muestra más grande es una aproximación mucho mejor a la verdadera distribución de la población que la más pequeña. Esto se refleja en los estadísticos muestrales. La media del CI de la muestra más grande es de 99,68 y la desviación estándar es 14,90. Estos valores ahora están muy próximos a la población real. Ver Figure 8.5.

Figure 8.5: Una muestra aleatoria extraída de una distribución normal usando jamovi

Me da un poco de vergüenza decirlo, pero lo que quiero que entiendas es que las muestras grandes suelen dar mejor información. Me da un poco de vergüenza decirlo porque es tan obvio que no hace falta decirlo. De hecho, es un punto tan obvio que cuando Jacob Bernoulli, uno de los fundadores de la teoría de la probabilidad, formalizó esta idea allá por 1713, fue un poco idiota al respecto. Así es como describió el hecho de que todos compartimos esta intuición:

Porque hasta el más estúpido de los hombres, por algún instinto de la naturaleza, por sí mismo y sin ninguna instrucción (lo cual es algo notable), está convencido de que cuantas más observaciones se han hecho, menor es el peligro de desviarse de propia la meta. (Stigler, 1986, p. 65).

De acuerdo, el pasaje resulta un poco condescendiente (por no decir sexista), pero su argumento principal es correcto. Es obvio que con más datos se obtienen mejores respuestas. La pregunta es: ¿por qué? No es sorprendente que esta intuición que todos compartimos resulte ser correcta, y los estadísticos se refieren a ella como la ley de los grandes números. La ley de los grandes números es una ley matemática que se aplica a muchos estadísticos muestrales diferentes, pero la forma más sencilla de entenderla es como una ley sobre promedios. La media muestral es el ejemplo más obvio de un estadístico que se basa en el promedio (porque eso es lo que es la media… un promedio), así que veámosla. Cuando se aplica a la media muestral, la ley de los grandes números establece que a medida que aumenta la muestra, la media muestral tiende a acercarse a la verdadera media de la población. O, para decirlo con un poco más de precisión, a medida que el tamaño de la muestra “se acerca” al infinito (escrito como \(N \longrightarrow \infty\)), la media muestral se acerca a la media poblacional \(\bar{X} \longrightarrow \mu\)) ³

No pretendo someterte a una prueba de que la ley de los grandes números es cierta, pero es una de las herramientas más importantes de la teoría estadística. La ley de los grandes números es lo que podemos usar para justificar nuestra creencia de que recoger cada vez más datos nos llevará finalmente a la verdad. Para cualquier conjunto de datos concreto, los estadísticos muestrales que calculemos a partir de él serán erróneos, pero la ley de los grandes números nos dice que si seguimos recopilando más datos, esos estadísticos muestrales tenderán a acercarse cada vez más a los verdaderos parámetros poblacionales.

8.3 Distribuciones muestrales y el teorema central del límite

La ley de los grandes números es una herramienta muy poderosa, pero no va a ser suficiente para responder a todas nuestras preguntas. Entre otras cosas, lo único que nos da es una “garantía a largo plazo”. A largo plazo, si de alguna manera pudiéramos recopilar una cantidad infinita de datos, la ley de los grandes números nos garantizaría que nuestros estadísticos muestrales serían correctos. Pero, como dijo John Maynard Keynes en economía, una garantía a largo plazo sirve de poco en la vida real.

[El] largo plazo es una guía engañosa de la actualidad. A largo plazo, todos estaremos muertos. Los economistas se imponen una tarea demasiado fácil, demasiado inútil, si en las estaciones tempestuosas solo pueden decirnos que cuando la tormenta ha pasado hace tiempo, el océano vuelve a estar plano. (Keynes, 1923, p. 80).

Como en economía, también en psicología y estadística. No basta con saber que al final llegaremos a la respuesta correcta cuando calculemos la media muestral. Saber que un conjunto de datos infinitamente grande me dirá el valor exacto de la media poblacional es un consuelo frío cuando mi conjunto de datos real tiene un tamaño de muestra de \(N = 100\). En la vida real, por tanto, debemos saber algo sobre el comportamiento de la media muestral cuando se calcula a partir de un conjunto de datos más modesto.

8.3.1 Distribución muestral de la media

Teniendo esto en cuenta, abandonemos la idea de que nuestros estudios tendrán tamaños de muestra de 10.000 y consideremos en su lugar un experimento muy modesto. Esta vez tomaremos una muestra de \(N = 5\) personas y mediremos sus puntuaciones de CI. Como antes, puedo simular este experimento en la función jamovi = NORM(100,15), pero esta vez solo necesito 5 ID de participantes, no 10,000. Estos son los cinco números que generó jamovi:

90 82 94 99 110

El CI medio en esta muestra resulta ser exactamente 95. No es sorprendente que sea mucho menos preciso que el experimento anterior. Ahora imaginemos que decido replicar el experimento. Es decir, repito el experimento lo más fielmente posible y tomo al azar una muestra de 5 personas nuevas y mido su CI. De nuevo, jamovi me permite simular los resultados de este procedimiento y genera estos cinco números:

78 88 111 111 117

Esta vez, el CI medio en mi muestra es 101. Si repito el experimento 10 veces, obtengo los resultados que se muestran en Table 8.1 y, como se puede ver, la media de la muestra varía de una repetición a otra.

Table 8.1:

Diez repeticiones del experimento CI, cada una con un tamaño de muestra de (N=5)

	Person 1	Person 2	Person 3	Person 4	Person 5	Sample Mean
Rep. 1	90	82	94	99	110	95.0
Rep. 2	78	88	111	111	117	101.0
Rep. 3	111	122	91	98	86	101.6
Rep. 4	98	96	119	99	107	103.8
Rep. 5	105	113	103	103	98	104.4
Rep. 6	81	89	93	85	114	92.4
Rep. 7	100	93	108	98	133	106.4
Rep. 8	107	100	105	117	85	102.8
Rep. 9	86	119	108	73	116	100.4
Rep. 10	95	126	112	120	76	105.8

Supongamos ahora que decido seguir así, replicando este experimento de “cinco puntuaciones de CI” una y otra vez. Cada vez que reproduzco el experimento anoto la media muestral. Con el tiempo, estaría acumulando un nuevo conjunto de datos, en el que cada experimento genera un único punto de datos. Las primeras 10 observaciones de mi conjunto de datos son las medias muestrales enumeradas en Table 8.1, por lo que mi conjunto de datos comienza así:

95,0 101,0 101,6 103,8 104,4 …

¿Y si continuara así durante 10,000 repeticiones y luego dibujara un histograma? Bueno, eso es exactamente lo que hice, y puedes ver los resultados en Figure 8.6. Como ilustra esta imagen, el promedio de 5 puntuaciones de CI suele estar entre 90 y 110. Pero lo que es más importante, lo que pone de relieve es que si replicamos un experimento una y otra vez, ¡lo que obtenemos al final es una distribución de medias muestrales! (Table 8.1)) Esta distribución tiene un nombre especial en estadística, se llama distribución muestral de la media.

Figure 8.6: La distribución muestral de la media del ‘experimento de las cinco puntuaciones de CI’. Si se toma una muestra de 5 personas al azar y se calcula su CI promedio, es casi seguro que se obtendrá un número entre 80 y 120, aunque hay bastantes personas que tienen CI superiores a 120 o inferiores a 80. A modo de comparación, la línea negra muestra la distribución poblacional de las puntuaciones de CI

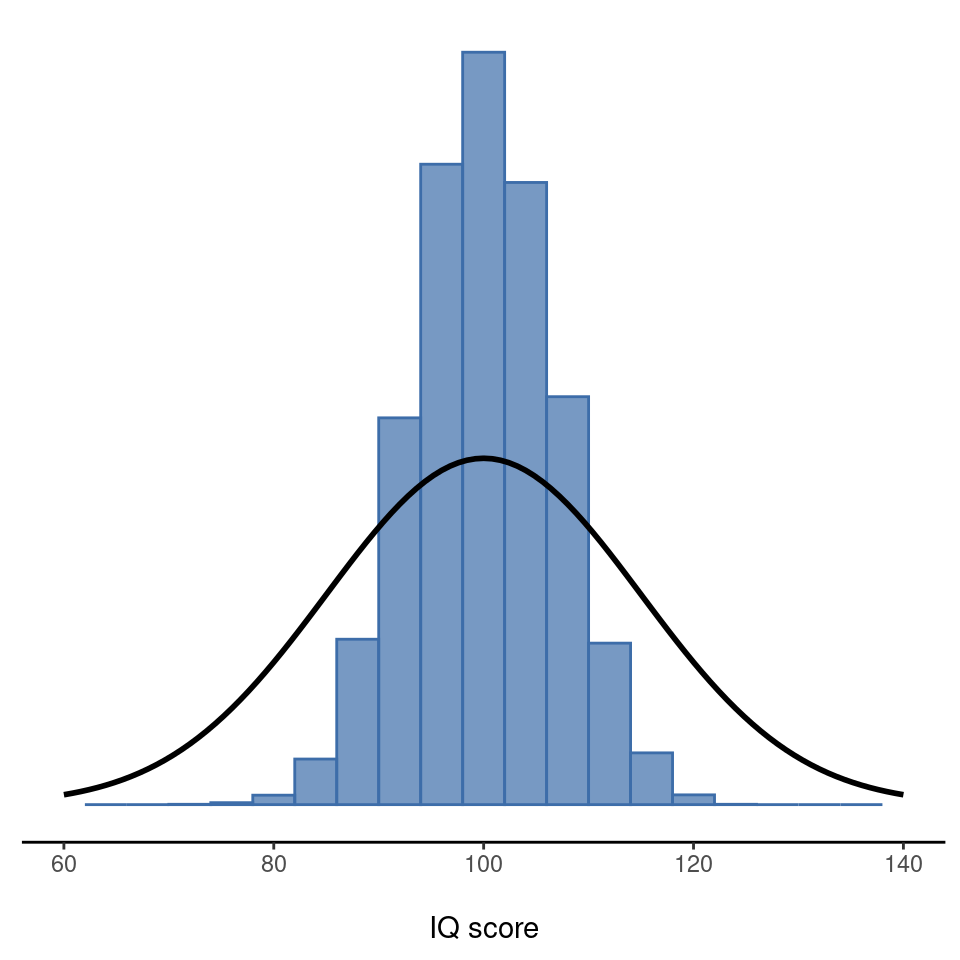
Las distribuciones muestrales son otra idea teórica importante en estadística, y son cruciales para comprender el comportamiento de las muestras pequeñas. Por ejemplo, cuando realicé el primer experimento de “cinco puntuaciones de CI”, la media de la muestra resultó ser 95. Sin embargo, lo que nos dice la distribución muestral en Figure 8.6 es que el experimento de “cinco puntuaciones de CI” no es muy preciso. Si repito el experimento, la distribución muestral me dice que puedo esperar ver una media muestral entre 80 y 120.

8.3.2 ¡Existen distribuciones muestrales para cualquier estadístico muestral!

Una cosa que hay que tener en cuenta cuando se piensa en distribuciones muestrales es que cualquier estadística muestral que quiera calcular tiene una distribución muestral. Por ejemplo, supongamos que cada vez que repito el experimento de las “cinco puntuaciones de CI” escribo la puntuación de CI más alta del experimento. Esto me daría un conjunto de datos que empezaría así:

110 117 122 119 113 …

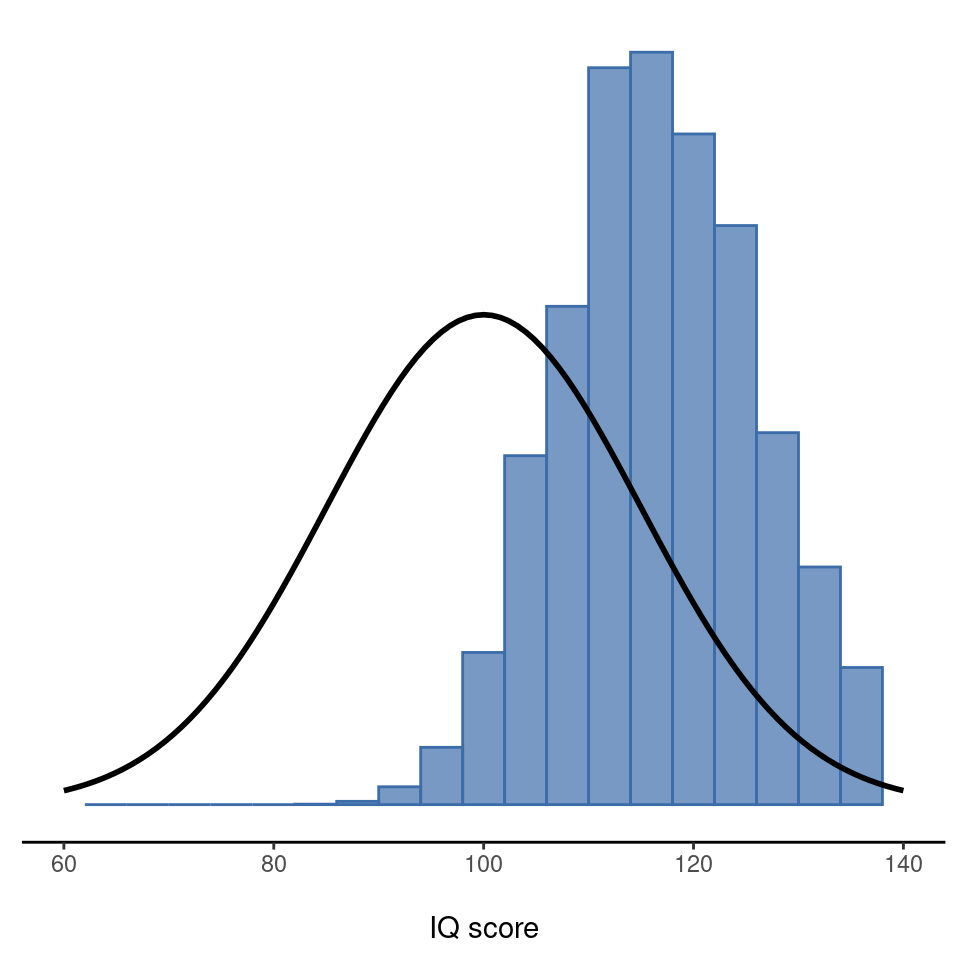
Hacer esto una y otra vez me daría una distribución muestral muy diferente, a saber, la distribución muestral del máximo. La distribución muestral del máximo de 5 puntuaciones de CI se muestra en Figure 8.7. No es de extrañar que si eliges a 5 personas al azar y luego encuentras a la persona con la puntuación de cociente intelectual más alta, vaya a tener un CI superior al promedio. La mayoría de las veces acabarás con alguien cuyo CI se mida en el rango de 100 a 140.

Figure 8.7: La distribución muestral del máximo para el ‘experimento de las cinco puntuaciones de CI’. Si tomas una muestra de 5 personas al azar y seleccionas a la que tenga la puntuación de CI más alta, probablemente verás a alguien con un CI entre 100 y 140.

Figure 8.8: Ilustración de cómo la distribución muestral de la media depende del tamaño de la muestra. En cada panel, he generado 10 000 muestras de datos de coeficiente intelectual y he calculado la media de CI observada en cada uno de estos conjuntos de datos. Los histogramas de estos gráficos muestran la distribución de estas medias (es decir, la distribución muestral de la media). Cada puntuación individual de CI se extrajo de una distribución normal con una media de 100 y una desviación estándar de 15, que se muestra como la línea negra continua. En el panel (a), cada conjunto de datos contiene una única observación, por lo que la media de cada muestra es la puntuación de CI de una sola persona. En consecuencia, la distribución muestral de la media es, por supuesto, idéntica a la distribución poblacional de las puntuaciones de CI. Sin embargo, cuando aumentamos el tamaño de la muestra a 2, la media de cualquier muestra tiende a estar más cerca de la media de la población que la puntuación de CI de cualquier persona, por lo que el histograma (es decir, la distribución muestral) es un poco más estrecho que la distribución de la población. En el momento en que aumentamos el tamaño de la muestra a 10 (panel (c)), podemos ver que la distribución de las medias muestrales tiende a agruparse bastante estrechamente en torno a la media real de la población.

8.3.3 El teorema central del límite

A estas alturas espero que tengas una idea bastante clara de lo que son las distribuciones muestrales y, en particular, de lo que es la distribución muestral de la media. En esta sección quiero hablar de cómo cambia la distribución muestral de la media en función del tamaño de la muestra. Intuitivamente, ya sabes parte de la respuesta. Si solo tienes unas pocas observaciones, es probable que la media muestral sea bastante inexacta. Si replicas un experimento pequeño y vuelves a calcular la media, obtendrás una respuesta muy diferente. En otras palabras, la distribución muestral es bastante amplia. Si replicas un experimento grande y vuelves a calcular la media muestral, probablemente obtendrás la misma respuesta que obtuviste la última vez, por lo que la distribución muestral será muy estrecha. Puedes ver esto visualmente en Figure 8.8, que muestra que cuanto mayor es el tamaño de la muestra, más estrecha es la distribución de muestreo. Podemos cuantificar este efecto calculando la desviación estándar de la distribución de muestreo, que se denomina error estándar. El error estándar de un estadístico se suele denotar SE, y como normalmente nos interesa el error estándar de la media muestral, a menudo usamos el acrónimo SEM. Como se puede ver con solo mirar la imagen, a medida que aumenta el tamaño de la muestra \(N\), el SEM disminuye.

Bien, esa es una parte de la historia. Sin embargo, hay algo que he pasado por alto hasta ahora. Todos mis ejemplos hasta ahora se han basado en los experimentos de “puntuaciones de CI”, y como las puntuaciones de CI se distribuyen de forma aproximadamente normal, he supuesto que la distribución de la población es normal. ¿Y si no es normal? ¿Qué ocurre con la distribución muestral de la media? Lo sorprendente es que, sea cual sea la forma de la distribución de la población, a medida que N aumenta, la distribución muestral de la media empieza a parecerse más a una distribución normal. Para que te hagas una idea, he realizado algunas simulaciones. Para ello, empecé con la distribución “en rampa” que se muestra en el histograma en Figure 8.9. Como se puede ver al comparar el histograma de forma triangular con la curva de campana trazada por la línea negra, la distribución de la población no se parece mucho a una distribución normal. A continuación, simulé los resultados de un gran número de experimentos. En cada experimento, tomé \(N = 2\) muestras de esta distribución y calculé la media muestral. Figure 8.9 (b) representa el histograma de estas medias muestrales (es decir, la distribución muestral de la media para \(N = 2\)). Esta vez, el histograma produce una distribución en forma de \(\chi^2\). Sigue sin ser normal, pero está mucho más cerca de la línea negra que la distribución de la población en Figure 8.9 (a). Cuando aumento el tamaño de la muestra a \(N = 4\), la distribución muestral de la media es muy cercana a la normal (Figure 8.9 (c)), y cuando llegamos a un tamaño de muestra de N = 8 es casi perfectamente normal. En otras palabras, mientras el tamaño de la muestra no sea pequeño, la distribución muestral de la media será aproximadamente normal, ¡independientemente de cómo sea la distribución de la población!

Figure 8.9: Demostración del teorema central del límite. En el panel (a), tenemos una distribución de población no normal, y los paneles (b)-(d) muestran la distribución muestral de la media para muestras de tamaño 2, 4 y 8 para datos extraídos de la distribución en el panel (a). Como se puede ver, aunque la distribución original de la población no es normal, la distribución muestral de la media se aproxima bastante a la normalidad cuando se tiene una muestra de 4 observaciones.

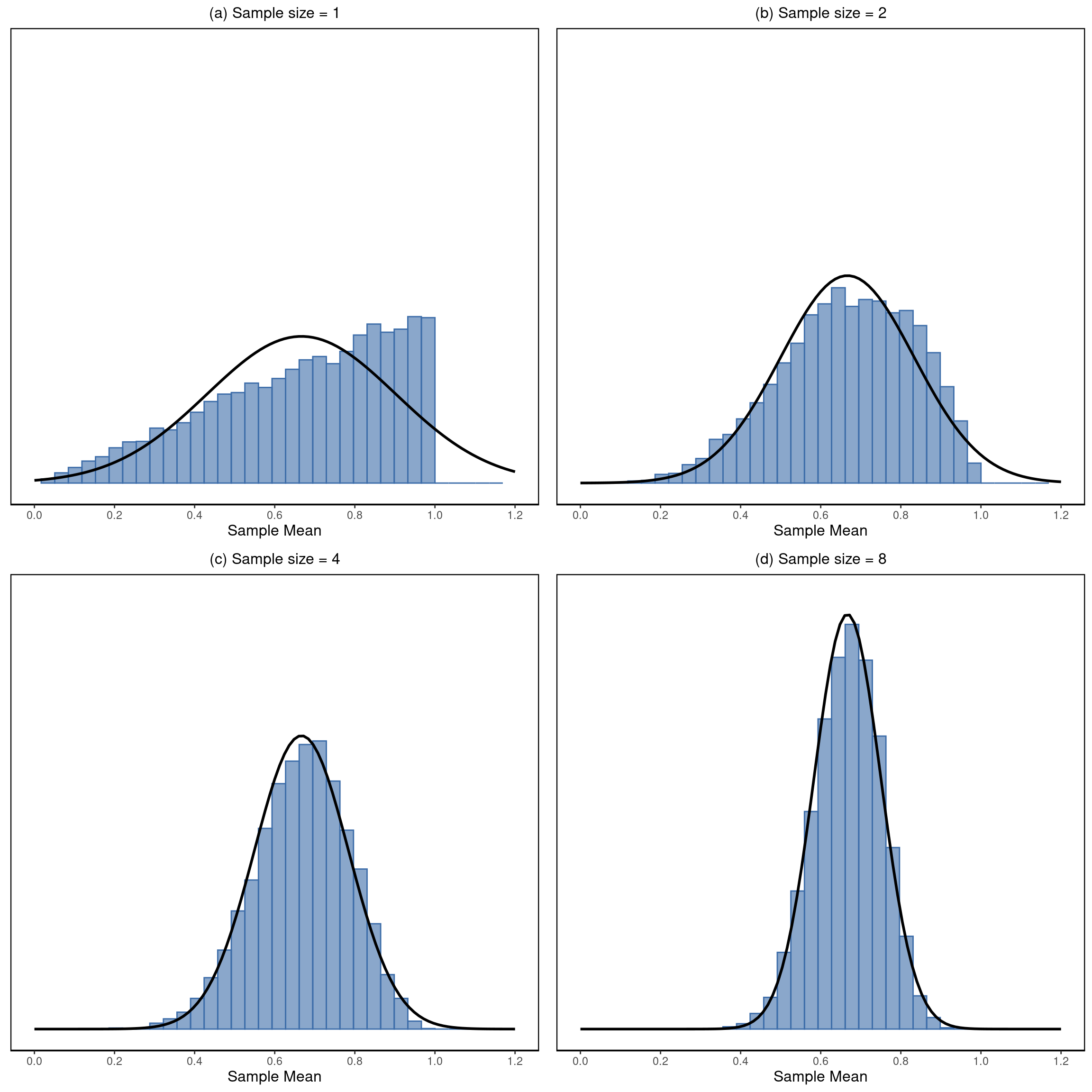
A partir de estas cifras, parece que tenemos pruebas de todas las afirmaciones siguientes sobre la distribución muestral de la media.

• La media de la distribución muestral es la misma que la media de la población
• La desviación estándar de la distribución muestral (es decir, el error estándar) disminuye a medida que aumenta el tamaño de la muestra
• La forma de la distribución muestral se vuelve normal a medida que aumenta el tamaño de la muestra.

Resulta que no solo todas estas afirmaciones son ciertas, sino que hay un teorema muy famoso en estadística que demuestra las tres cosas, conocido como el teorema central del límite. Entre otras cosas, el teorema central del límite nos dice que si la distribución de la población tiene media \(\mu\) y desviación estándar \(\sigma\), entonces la distribución muestral de la media también tiene media \(\mu\) y el error estándar de la media es

\[SEM=\frac{\sigma}{\sqrt{N}}\]

Como dividimos la desviación estándar de la población \(\sigma\) por la raíz cuadrada del tamaño de la muestra N, el SEM se hace más pequeño a medida que aumenta el tamaño de la muestra. También nos dice que la forma de la distribución muestral se vuelve normal.⁴

Este resultado es útil para todo tipo de cosas. Nos dice por qué los experimentos grandes son más fiables que los pequeños, y como nos da una fórmula explícita para el error estándar, nos dice cuánto más fiable es un experimento grande. Nos dice por qué la distribución normal es, bueno, normal. En los experimentos reales, muchas de las cosas que queremos medir son en realidad promedios de muchas cantidades diferentes (por ejemplo, podría decirse que la inteligencia “general” medida por el CI es un promedio de una gran cantidad de habilidades y capacidades “específicas”), y cuando esto ocurre, la cantidad promediada debería seguir una distribución normal. Debido a esta ley matemática, la distribución normal aparece una y otra vez en los datos reales.

8.4 Estimación de los parámetros poblacionales

En todos los ejemplos de CI de las secciones anteriores conocíamos de antemano los parámetros de la población. Como se enseña a todos los estudiantes universitarios en su primera lección sobre la medición de la inteligencia, las puntuaciones del CI se definen con una media de 100 y una desviación estándar de 15. Sin embargo, esto es un poco mentira. ¿Cómo sabemos que las puntuaciones de CI tienen una media poblacional real de 100? Bueno, lo sabemos porque las personas que diseñaron los tests los han administrado a muestras muy grandes y luego han “amañado” las reglas de puntuación para que su muestra tenga una media de 100. Eso no es malo, por supuesto, es una parte importante del diseño de una medida psicológica. Sin embargo, es importante tener en cuenta que esta media teórica de 100 solo se aplica a la población que los diseñadores de los tests usaron para diseñarlos. De hecho, los buenos diseñadores de tests harán todo lo posible para proporcionar “normas de tests” que puedan aplicarse a muchas poblaciones diferentes (por ejemplo, diferentes grupos de edad, nacionalidades, etc.).

Esto es muy práctico, pero, por supuesto, casi todos los proyectos de investigación de interés implican analizar una población de personas diferente a la utilizada en las normas de la prueba. Por ejemplo, supongamos que queremos medir el efecto de la intoxicación por plomo de bajo nivel en el funcionamiento cognitivo en Port Pirie, una ciudad industrial del sur de Australia con una fundición de plomo. Tal vez decidas comparar las puntuaciones de CI entre las personas de Port Pirie con una muestra comparable de Whyalla, una ciudad industrial del sur de Australia con una refinería de acero.⁵ Independientemente de la ciudad en la que estés pensando, no tiene mucho sentido suponer simplemente que la media real de CI de la población sea 100. Que yo sepa, nadie ha elaborado datos normativos razonables que puedan aplicarse automáticamente a las ciudades industriales del sur de Australia. Tendremos que estimar los parámetros de la población a partir de una muestra de datos. ¿Y cómo lo hacemos?

8.4.1 Estimación de la media poblacional

Supongamos que vamos a Port Pirie y 100 de los lugareños tienen la amabilidad de someterse a un test de CI. La puntuación media de CI entre estas personas resulta ser \(\bar{X}=98.5\). Entonces, ¿cuál es el verdadero CI medio de toda la población de Port Pirie? Obviamente, no sabemos la respuesta a esa pregunta. Podría ser 97,2, pero también podría ser 103,5. Nuestro muestreo no es exhaustivo, así que no podemos dar una respuesta definitiva. No obstante, si me obligaran a punta de pistola a dar una “mejor estimación”, tendría que decir que es 98.5. Esa es la esencia de la estimación estadística: dar la mejor estimación posible.

En este ejemplo, la estimación del parámetro de población desconocido es sencilla. Calculo la media muestral y la utilizo como mi estimación de la media poblacional. Es bastante sencillo, y en la siguiente sección explicaré la justificación estadística de esta respuesta intuitiva. Sin embargo, por el momento lo que quiero hacer es asegurarme de que reconoces que el estadístico muestral y la estimación del parámetro poblacional son cosas conceptualmente diferentes. Un estadístico muestral es una descripción de tus datos, mientras que la estimación es una conjetura sobre la población. Teniendo esto en cuenta, los estadísticos suelen utilizar diferentes notaciones para referirse a ellos. Por ejemplo, si la media poblacional verdadera se denota \(\mu\), entonces usaríamos \(\hat{\mu}\) para referirnos a nuestra estimación de la media poblacional. En cambio, la media muestral se denota \(\bar{X}\) o, a veces, m. Sin embargo, en muestras aleatorias simples la estimación de la media poblacional es idéntica a la media muestral. Si observo una media muestral de \(\bar{X}=98,5\), entonces mi estimación de la media poblacional también es \(\hat{\mu}=98,5\). Para ayudar a mantener clara la notación, aquí hay una tabla práctica (Table 8.2):

Table 8.2:

Notación para la media

Symbol	What is it?	Do we know what it is?
\( \hat{X} \)	Sample mean	Yes, calculated from the raw data
\( \mu \)	True population mean	Almost never known for sure
\( \hat{\mu} \)	Estimate of the population mean	Yes, identical to the sample mean in simple random samples

8.4.2 Estimación de la desviación estándar de la población

Hasta ahora, la estimación parece bastante sencilla, y puede que te preguntes por qué te he obligado a leer todo eso sobre la teoría del muestreo. En el caso de la media, nuestra estimación del parámetro poblacional (es decir, \(\hat{\mu}\)) resultó ser idéntica al estadístico muestral correspondiente (es decir, \(\bar{X}\)). Sin embargo, esto no siempre es cierto. Para verlo, pensemos en cómo construir una estimación de la desviación estándar poblacional, que denotaremos \(\hat{\sigma}\). ¿Qué utilizaremos como estimación en este caso? Tu primer pensamiento podría ser que podríamos hacer lo mismo que hicimos al estimar la media, y sólo tienes que utilizar el estadístico muestral como nuestra estimación. Eso es casi lo correcto, pero no del todo.

He aquí por qué. Supongamos que tengo una muestra que contiene una única observación. Para este ejemplo, es útil considerar una muestra en la que no tengas ninguna intuición sobre cuáles podrían ser los valores reales de la población, así que usemos algo completamente ficticio. Supongamos que la observación en cuestión mide la cromulencia de mis zapatos. Resulta que mis zapatos tienen una cromulencia de \(20\). Así que aquí está mi muestra:

Se trata de una muestra perfectamente legítima, aunque tenga un tamaño muestral de \(N = 1\). Tiene una media muestral de \(20\) y dado que cada observación de esta muestra es igual a la media muestral (¡obviamente!) tiene una desviación estándar muestral de 0. Como descripción de la muestra parece bastante correcta, la muestra contiene una única observación y, por tanto, no se observa ninguna variación dentro de la muestra. Una desviación estándar muestral de \(s = 0\) es la respuesta correcta en este caso. Pero como estimación de la desviación estándar de la población parece una completa locura, ¿verdad? Es cierto que tú y yo no sabemos nada en absoluto sobre lo que es la “cromulencia”, pero sabemos algo sobre datos. La única razón por la que no vemos ninguna variabilidad en la muestra es que la muestra es demasiado pequeña para mostrar ninguna variación. Por lo tanto, si tenemos un tamaño de muestra de \(N = 1\), parece que la respuesta correcta es simplemente decir “ni idea”.

Observa que no tienes la misma intuición cuando se trata de la media muestral y la media poblacional. Si nos vemos obligadas a hacer una suposición sobre la media de la población, no nos parecerá una locura adivinar que la media de la población es \(20\). Claro, probablemente no te sentirías muy segura de esa suposición porque solo tienes una observación con la que trabajar, pero sigue siendo la mejor suposición que puedes hacer.

Ampliemos un poco este ejemplo. Supongamos que ahora hago una segunda observación. Mi conjunto de datos ahora tiene \(N = 2\) observaciones de la cromulencia de los zapatos, y la muestra completa tiene ahora este aspecto:

\[20, 22\]

Esta vez, nuestra muestra es lo suficientemente grande como para que podamos observar cierta variabilidad: ¡dos observaciones es el número mínimo necesario para observar cualquier variabilidad! Para nuestro nuevo conjunto de datos, la media muestral es \(\bar{X} = 21\) y la desviación estándar muestral es \(s = 1\). ¿Qué intuiciones tenemos sobre la población? Una vez más, en lo que respecta a la media poblacional, la mejor suposición que podemos hacer es la media muestral. Si tuviéramos que adivinar, probablemente diríamos que la cromulencia media de la población es de \(21\). ¿Qué pasa con la desviación estándar? Esto es un poco más complicado. La desviación estándar de la muestra solo se basa en dos observaciones, y si eres como yo, probablemente tengas la intuición de que, con solo dos observaciones, no le hemos dado a la población “suficientes oportunidades” para que nos revele su verdadera variabilidad. a nosotros. No es solo que sospechemos que la estimación es incorrecta, después de todo, con solo dos observaciones esperamos que lo sea en cierta medida. Lo que nos preocupa es que el error sea sistemático. En concreto, sospechamos que es probable que la desviación estándar de la muestra sea menor que la desviación estándar de la población.

Esta intuición parece correcta, pero estaría bien poder demostrarlo de alguna manera. De hecho, existen pruebas matemáticas que confirman esta intuición, pero a menos que se tengan los conocimientos matemáticos adecuados, no sirven de mucho. En cambio, lo que haré será simular los resultados de algunos experimentos. Con eso en mente, volvamos a nuestros estudios sobre el CI. Supongamos que la media real de CI de la población es de \(100\) y la desviación estándar es de \(15\). Primero realizaré un experimento en el que mediré \(N = 2\) puntuaciones de CI y calcularé la desviación estándar de la muestra. Si hago esto una y otra vez y trazo un histograma de estas desviaciones estándar muestrales, lo que tengo es la distribución muestral de la desviación estándar. He representado esta distribución en Figure 8.10. Aunque la verdadera desviación estándar de la población es 15, la media de las desviaciones estándar muestrales es solo 8.5. Observa que este es un resultado muy diferente al que encontramos en Figure 8.8 (b) cuando trazamos la distribución muestral de la media, donde la media poblacional es \(100\) y la media de las medias muestrales también es \(100\) .

[1] 8.498853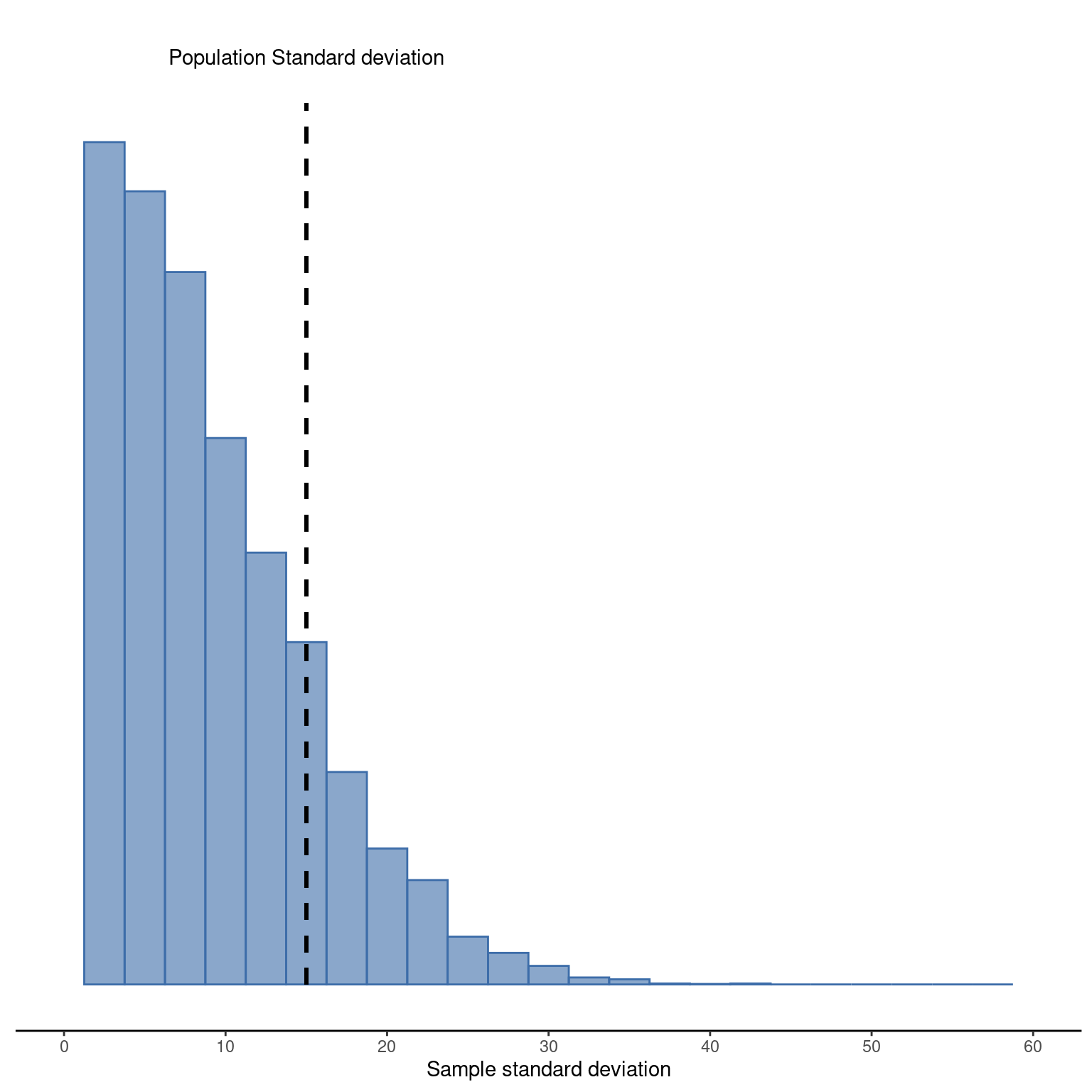

Figure 8.10: Distribución muestral de la desviación estándar muestral para un experimento de ‘dos puntuaciones de CI’. La verdadera desviación estándar de la población es 15 (línea discontinua), pero como se puede ver en el histograma, la gran mayoría de los experimentos producirán una desviación estándar muestral mucho menor que esta. En promedio, este experimento produciría una desviación estándar estimada de solo 8,4, ¡muy por debajo del valor real! En otras palabras, la desviación estándar de la muestra es una estimación sesgada de la desviación estándar de la población.

Ahora ampliemos la simulación. En lugar de limitarnos a la situación en la que \(N=2\), repitamos el ejercicio para tamaños de muestra de 1 a 10. Si representamos gráficamente la media muestral promedio y la desviación estándar muestral promedio en función del tamaño de la muestra, obtendremos los resultados que se muestran en Figure 8.11. En el lado izquierdo (panel (a)) he representado la media muestral promedio y en el lado derecho (panel (b)) he representado la desviación estándar promedio. Los dos gráficos son bastante diferentes: en promedio, la media muestral promedio es igual a la media poblacional. Es un estimador insesgado, que es esencialmente la razón por la que la mejor estimación de la media poblacional es la media muestral.⁶ El gráfico de la derecha es bastante diferente: en promedio, la desviación estándar muestral \(s\) es menor que la desviación estándar poblacional \(\sigma\). Se trata de un estimador sesgado. En otras palabras, si queremos hacer una “mejor estimación” \(\hat{\sigma}\) sobre el valor de la desviación estándar poblacional \(\hat{\sigma}\) debemos asegurarnos de que nuestra estimación es un poco mayor que la desviación estándar muestral \(s\).

Figure 8.11: Ilustración del hecho de que la media muestral es un estimador insesgado de la media poblacional (panel a), pero la desviación estándar muestral es un estimador sesgado de la desviación estándar poblacional (panel b). Para la figura, generé conjuntos de datos simulados de $ 10,000 $ con 1 observación cada uno, $ 10,000 $ más con 2 observaciones, y así sucesivamente hasta un tamaño de muestra de 10. Cada conjunto de datos estaba formado por datos de CI falsos, es decir, los datos se distribuían normalmente con una media poblacional real de 100 y una desviación estándar de 15. En promedio, las medias muestrales resultan ser 100, independientemente del tamaño de la muestra (panel a). Sin embargo, las desviaciones estándar de la muestra resultan ser sistemáticamente demasiado pequeñas (panel b), sobre todo para tamaños de muestra pequeños.

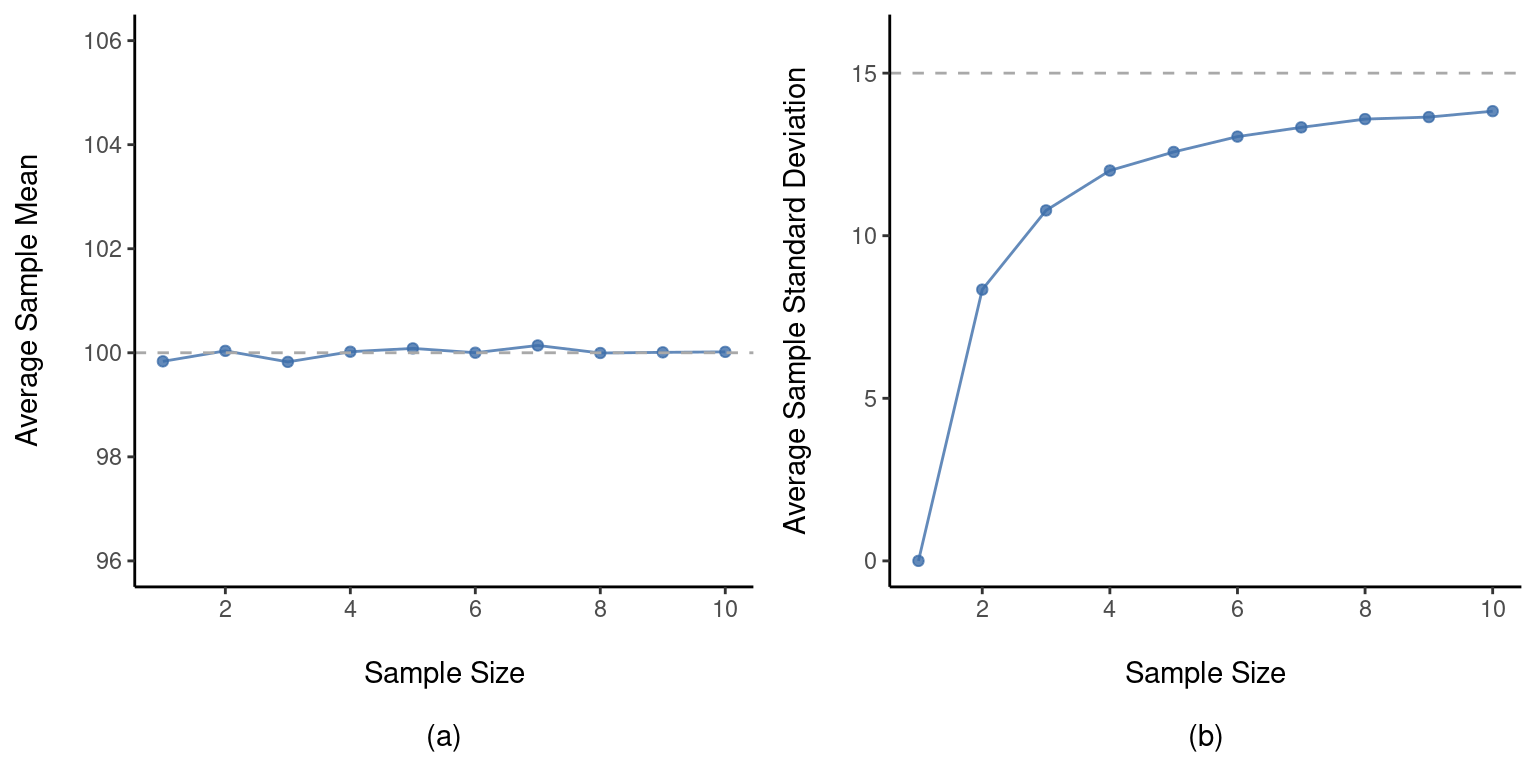
La solución a este sesgo sistemático es muy sencilla. Así es como funciona. Antes de abordar la desviación estándar, veamos la varianza. Si recuerdas la sección sobre [Estimación de los parámetros de la población], la varianza de la muestra se define como la media de las desviaciones al cuadrado de la media de la muestra. Es decir: \[s^2=\frac{1}{N} \sum_{i=1}^{N}(X_i-\bar{X})^2\] La varianza muestral \(s^2\) es un estimador sesgado de la varianza poblacional \(\sigma^2\). Pero resulta que solo tenemos que hacer un pequeño ajuste para transformar esto en un estimador insesgado. Todo lo que tenemos que hacer es dividir por \(N-1\) en lugar de por \(N\).

Se trata de un estimador insesgado de la varianza poblacional \(\sigma\). Además, esto responde finalmente a la pregunta que planteamos en [Estimación de los parámetros de la población]. ¿Por qué jamovi nos da respuestas ligeramente diferentes para la varianza? Es porque jamovi calcula \(\hat{\sigma}^2 \text{ no } s^2\), por eso. Una historia similar se aplica a la desviación estándar. Si dividimos entre \(N - 1\) en lugar de \(N\), nuestra estimación de la desviación estándar de la población es insesgada, y cuando usamos la función de desviación estándar de jamovi, lo que está haciendo es calcular \(\hat{\sigma}\) no $ s$.⁷

Un último punto. En la práctica, mucha gente tiende a referirse a \(\hat{\sigma}\) (es decir, la fórmula en la que dividimos por \(N - 1\)) como la desviación estándar de la muestra. Técnicamente, esto es incorrecto. La desviación estándar de la muestra debería ser igual a s (es decir, la fórmula en la que dividimos por N). No son lo mismo, ni conceptual ni numéricamente. Una es una propiedad de la muestra, la otra es una característica estimada de la población. Sin embargo, en casi todas las aplicaciones de la vida real, lo que realmente nos importa es la estimación del parámetro de la población, por lo que la gente siempre informa \(\hat{\sigma}\) en lugar de s. Este es el número correcto para informar, por supuesto. Es solo que la gente tiende a ser un poco imprecisa con la terminología cuando lo escriben, porque “desviación estándar de la muestra” es más corta que “desviación estándar estimada de la población”. No es gran cosa, y en la práctica hago lo mismo que todo el mundo. Sin embargo, creo que es importante mantener los dos conceptos separados. Nunca es buena idea confundir “propiedades conocidas de la muestra” con “suposiciones sobre la población de la que procede”. En el momento en que empiezas a pensar que \(s\) y \(\hat{\sigma}\) son lo mismo, empiezas a hacer exactamente eso.

Para terminar esta sección, aquí hay otro par de tablas para ayudar a mantener las cosas claras (Table 8.3 y Table 8.4).

Table 8.3:

Notación para la desviación estándar

Symbol	What is it?	Do we know what it is?
\( s \)	Sample standard deviation	Yes, calculated from the raw data
\( \sigma \)	Population standard deviation	Almost never known for sure
\( \hat{\sigma } \)	Estimate of the population standard deviation	Yes, but not the same as the sample standard deviation

Table 8.4:

Notación para la varianza

Symbol	What is it?	Do we know what it is?
\( s^2 \)	Sample variance	Yes, calculated from the raw data
\( \sigma^2 \)	Population variance	Almost never known for sure
\( \hat{\sigma }^2 \)	Estimate of the population variance	Yes, but not the same as the sample variance

8.5 Estimación de un intervalo de confianza

Estadística significa nunca tener que decir que estás seguro
– Origen desconocido ⁸

Hasta este punto del capítulo, he descrito los fundamentos de la teoría del muestreo en la que se basan los estadísticos para hacer conjeturas sobre los parámetros de la población a partir de una muestra de datos. Como ilustra esta discusión, una de las razones por las que necesitamos toda esta teoría del muestreo es que cada conjunto de datos nos deja algo de incertidumbre, por lo que nuestras estimaciones nunca van a ser perfectamente precisas. Lo que ha faltado en este debate es un intento de cuantificar la cantidad de incertidumbre que acompaña a nuestra estimación. No basta con adivinar que, por ejemplo, el CI medio de los estudiantes universitarios de psicología es de 115 dólares (sí, me acabo de inventar esa cifra). También queremos poder decir algo que exprese el grado de certeza que tenemos en nuestra conjetura. Por ejemplo, estaría bien poder decir que hay un \(95\%\) de probabilidades de que la verdadera media se encuentre entre \(109\) y \(121\). El nombre para esto es un intervalo de confianza para la media.

Si se conocen las distribuciones muestrales, construir un intervalo de confianza para la media es bastante fácil. Así es como funciona. Supongamos que la media real de la población es \(\mu\) y la desviación estándar es \(\sigma\). Acabo de terminar mi estudio que tiene N participantes, y la media del CI entre esos participantes es \(\bar{X}\). Sabemos por nuestra discusión de El teorema central del límite que la distribución muestral de la media es aproximadamente normal. También sabemos por nuestra discusión sobre la distribución normal en Section 7.5 que existe una probabilidad de \(95\%\) de que una cantidad distribuida normalmente caiga dentro de aproximadamente dos desviaciones estándar de la media real.

Para ser más precisos, la respuesta más correcta es que existe una probabilidad del \(95\%\) de que una cantidad distribuida normalmente caiga dentro de \(1,96\) desviaciones estándar de la media real. A continuación, recordemos que la desviación estándar de la distribución muestral se denomina error estándar y el error estándar de la media se escribe como SEM. Cuando juntamos todas estas piezas, aprendemos que existe una probabilidad del 95% de que la media muestral \(\bar{X}\) que hemos observado realmente se encuentre dentro de \(1,96\) errores estándar de la media poblacional.

Por supuesto, el número \(1.96\) no tiene nada de especial. Resulta que es el multiplicador que hay que utilizar si se desea un intervalo de confianza de \(95\%\). Si hubieras querido un intervalo de confianza de \(70\%\), habrías usado \(1,04\) como número mágico en lugar de \(1,96\).

[Detalle técnico adicional ⁹]

Por supuesto, no hay nada especial en el número 1,96. Resulta que es el multiplicador que necesita usar si desea un intervalo de confianza del 95%. Si hubiera querido un intervalo de confianza del 70 %, habría utilizado 1,04 como número mágico en lugar de 1,96.

8.5.1 Interpretar un intervalo de confianza

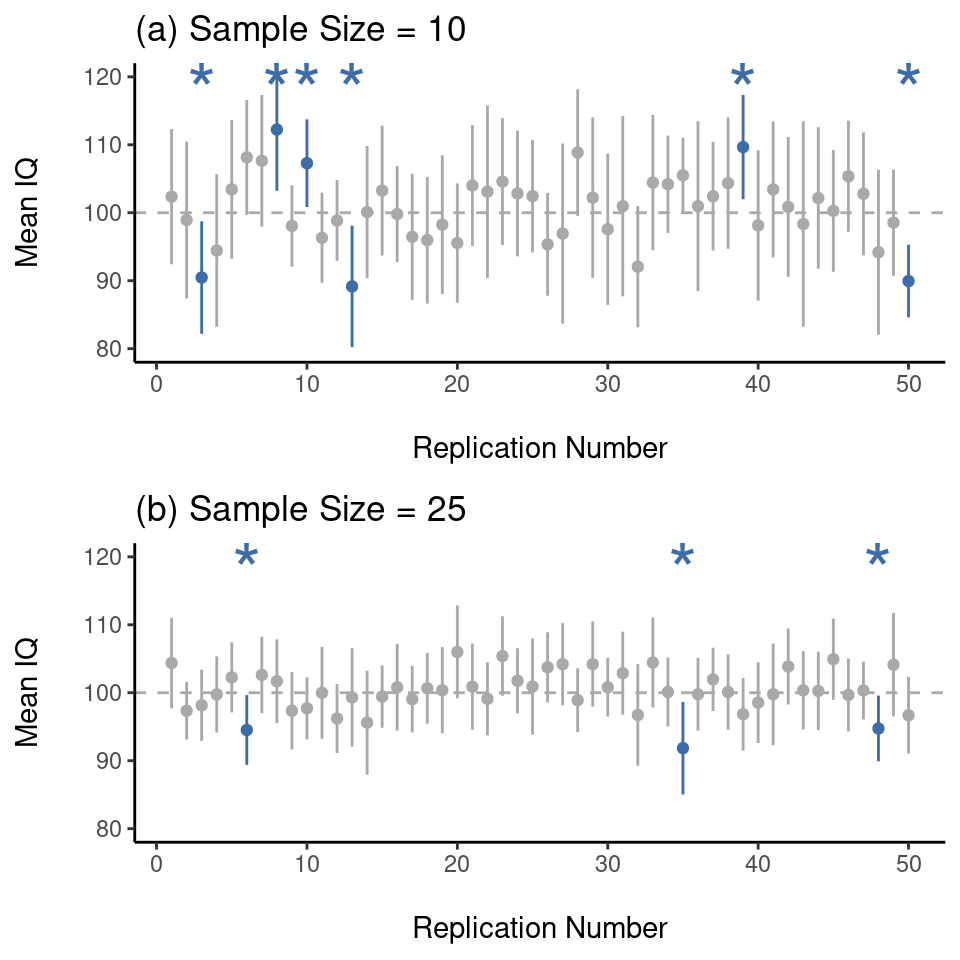
Lo más difícil de los intervalos de confianza es entender lo que significan. Cuando la gente se encuentra por primera vez con intervalos de confianza, el primer instinto casi siempre es decir que “hay un 95% de probabilidad de que la media real se encuentre dentro del intervalo de confianza”. Es sencillo y parece captar la idea de sentido común de lo que significa decir que tengo un “95% de confianza”. Por desgracia, no es del todo correcto. La definición intuitiva depende en gran medida de las creencias personales sobre el valor de la media de la población. Digo que tengo un 95% de confianza porque esas son mis creencias. En la vida cotidiana eso está perfectamente bien, pero si recuerdas la sección [¿Qué significa probabilidad?], te darás cuenta de que hablar de creencias personales y confianza es una idea bayesiana. Sin embargo, los intervalos de confianza no son herramientas bayesianas. Como todo lo demás en este capítulo, los intervalos de confianza son herramientas frecuentistas, y si vas a utilizar métodos frecuentistas, entonces no es apropiado darles una interpretación bayesiana. Si utilizas métodos frecuentistas, debes adoptar interpretaciones frecuentistas. Bien, si esa no es la respuesta correcta, ¿cuál es? Recuerda lo que dijimos sobre la probabilidad frecuentista. La única forma que tenemos de hacer “afirmaciones de probabilidad” es hablar de una secuencia de sucesos y contar las frecuencias de los diferentes sucesos. Desde esa perspectiva, la interpretación de un intervalo de confianza del 95% debe tener algo que ver con la replicación. En concreto, si replicamos el experimento una y otra vez y calculamos un intervalo de confianza del 95% para cada repetición, entonces el 95% de esos intervalos contendrían la media verdadera. De manera más general, el 95% de todos los intervalos de confianza construidos mediante este procedimiento deberían contener la media poblacional verdadera. Esta idea se ilustra en Figure 8.12, que muestra 50 intervalos de confianza construidos para un experimento de “medida de 10 puntuaciones de CI” (panel superior) y otros 50 intervalos de confianza para un experimento de “medida de 25 puntuaciones de CI” (panel inferior). Esperaríamos que alrededor de 95 de nuestros intervalos de confianza contuvieran la verdadera media poblacional, y eso es lo que encontramos en Figure 8.12. La diferencia fundamental aquí es que la afirmación bayesiana hace una declaración de probabilidad sobre la media de la población (es decir, se refiere a nuestra incertidumbre sobre la media de la población), lo que no está permitido según la interpretación frecuentista de la probabilidad porque no se puede “replicar” una población. En la afirmación frecuentista, la media poblacional es fija y no se pueden hacer afirmaciones probabilísticas sobre ella. Sin embargo, los intervalos de confianza son repetibles, por lo que podemos replicar experimentos. Por lo tanto, un frecuentista puede hablar de la probabilidad de que el intervalo de confianza (una variable aleatoria) contenga la media real, pero no puede hablar de la probabilidad de que la media poblacional real (no es un suceso repetible) se encuentre dentro del intervalo de confianza. Sé que esto parece un poco pedante, pero es importante. Importa porque la diferencia en la interpretación conduce a una diferencia en las matemáticas. Existe una alternativa bayesiana a los intervalos de confianza, conocida como intervalos creíbles. En la mayoría de las situaciones, los intervalos creíbles son bastante similares a los intervalos de confianza, pero en otros casos son drásticamente diferentes. Sin embargo, como prometí, hablaré más sobre la perspectiva bayesiana en Chapter 16.

Figure 8.12: Intervalos de confianza del 95%. El panel superior (a) muestra 50 réplicas simuladas de un experimento en el que medimos el CI de 10 personas. El punto marca la posición de la media muestral y la línea muestra el intervalo de confianza del 95%. La mayoría de los 50 intervalos de confianza contienen media real (es decir, 100), pero algunos, en azul y marcados con asteriscos, no la contienen. El gráfico inferior (panel b) muestra una simulación similar, pero esta vez simulamos réplicas de un experimento que mide el CI de 25 personas.

8.5.2 Cálculo de intervalos de confianza en jamovi

jamovi incluye una forma sencilla de calcular los intervalos de confianza para la media como parte de la funcionalidad ‘Descriptivos’. En ‘Descriptivos’-‘Estadísticas’ hay una casilla de verificación tanto para ‘Error estándar de la media’ como para el ‘Intervalo de confianza para la media’, por lo que puedes usar esto para averiguar el intervalo de confianza del 95% (que es el valor predeterminado). Así, por ejemplo, si cargo el archivo IQsim.omv, marco la casilla ‘Intervalo de confianza para la media’, puedo ver el intervalo de confianza asociado con el CI medio simulado: IC del 95 % inferior = 99,39 y IC del 95 % superior = 99,97. Así, en nuestros datos de muestra grande con N = 10 000, la puntuación media del CI es 99,68 con un IC del 95 % de 99,39 a 99,97.

Cuando se trata de trazar intervalos de confianza en jamovi, puede especificar que la media se incluya como opción en un diagrama de caja. Además, cuando aprendamos sobre pruebas estadísticas específicas, por ejemplo, en Chapter 13, veremos que también podemos trazar intervalos de confianza como parte del análisis de datos. Eso está muy bien, así que te mostraremos cómo hacerlo más adelante.

8.6 Resumen

En este capítulo hemos tratado dos temas principales. La primera mitad del capítulo trata sobre la teoría del muestreo, y la segunda mitad trata sobre cómo podemos usar la teoría del muestreo para construir estimaciones de los parámetros de la población. El desglose de las secciones es el siguiente:

• Ideas básicas sobre Muestras, poblaciones y muestreo
• Teoría estadística del muestreo: La ley de los grandes números y Distribuciones muestrales y el teorema central del límite
• [Estimación de parámetros poblacionales]. Medias y desviaciones estándar
• Estimación de un intervalo de confianza

Como siempre, hay muchos temas relacionados con el muestreo y la estimación que no se tratan en este capítulo, pero creo que para una clase de introducción a la psicología es bastante completo. Para la mayoría de los investigadores aplicados, no necesitará mucha más teoría que esta. Una cuestión importante que no he tocado en este capítulo es qué hacer cuando no se dispone de una muestra aleatoria simple. Hay mucha teoría estadística a la que se puede recurrir para manejar esta situación, pero va mucho más allá del alcance de este libro.

Keynes, J. M. (1923). A tract on monetary reform. Macmillan; Company.

Stigler, S. M. (1986). The history of statistics. Harvard University Press.

---

1. La definición matemática correcta de aleatoriedad es extraordinariamente técnica y va mucho más allá del alcance de este libro. No seremos técnicas aquí y diremos que un proceso tiene un elemento de aleatoriedad siempre que sea posible repetir el proceso y obtener respuestas diferentes cada vez.

2. Nada en la vida es tan sencillo. No existe una división obvia de las personas en categorías binarias como “esquizofrénico” y “no esquizofrénico”. Pero este no es un texto de psicología clínica, así que os ruego que me perdonéis algunas simplificaciones aquí y allá.

3. Técnicamente, la ley de los grandes números se aplica a cualquier estadístico muestral que pueda describirse como un promedio de cantidades independientes. Esto es cierto para la media muestral. Sin embargo, también es posible escribir muchos otros estadísticos muestrales como promedios de una forma u otra. La varianza de una muestra, por ejemplo, se puede reescribir como un tipo de promedio y, por tanto, está sujeta a la ley de los grandes números. Sin embargo, el valor mínimo de una muestra no se puede escribir como un promedio de nada y, por lo tanto, no se rige por la ley de los grandes números.

4. Como de costumbre, estoy siendo un poco descuidada aquí. El teorema central del límite es un poco más general de lo que parece en esta sección. Como en la mayoría de los textos de introducción a la estadística, he tratado una situación en la que se cumple el teorema central del límite: cuando se toma la media de muchos sucesos independientes extraídos de la misma distribución. Sin embargo, el teorema central del límite es mucho más amplio que esto. Por ejemplo, hay toda una clase de cosas llamadas “estadísticos U”, todas las cuales cumplen el teorema central del límite y, por lo tanto, se distribuyen normalmente para muestras de gran tamaño. La media es uno de esos estadísticos, pero no es el único.

5. Ten en cuenta que si realmente estuvieras interesada en esta cuestión, tendrías que ser mucho más cuidadosa que yo. No se puede comparar sin más las puntuaciones de CI de Whyalla con las de Port Pirie y suponer que cualquier diferencia se debe a la intoxicación por plomo. Aunque fuera cierto que las únicas diferencias entre las dos ciudades correspondieran a las diferentes refinerías (y no lo es, ni mucho menos), hay que tener en cuenta que la gente ya cree que la contaminación por plomo provoca déficits cognitivos. Si volvemos a Chapter 2, esto significa que hay diferentes efectos de demanda para la muestra de Port Pirie que para la muestra de Whyalla. En otras palabras, es posible que los datos muestren una diferencia de grupo ilusoria en tus datos, causada por el hecho de que la gente cree que existe una diferencia real. Me parece bastante inverosímil pensar que los lugareños no se darían cuenta de lo que se estaba intentando hacer si un grupo de investigadores apareciera en Port Pirie con batas de laboratorio y tests de CI, y aún menos verosímil pensar que mucha gente estaría bastante resentida contigo por hacerlo. Esas personas no cooperarán tanto en las pruebas. Otras personas de Port Pirie podrían estar más motivadas para hacerlo bien porque no quieren que su ciudad natal quede mal. Es probable que los efectos motivacionales que se aplicarían en Whyalla sean más débiles, porque la gente no tiene el mismo concepto de “intoxicación por mineral de hierro” que de “intoxicación por plomo”. La psicología es difícil.

6. Debo señalar que estoy ocultando algo aquí. La insesgadez es una característica deseable para un estimador, pero hay otras cosas que importan además del sesgo. Sin embargo, está fuera del alcance de este libro discutir esto en detalle. Solo quiero llamar tu atención sobre el hecho de que hay una cierta complejidad oculta aquí.

7. Dividiendo por \(N-1\) obtenemos una estimación insesgada de la varianza poblacional: \[\hat{\sigma}^2=\frac{1}{N-1}\sum_{i=1}^{N}( X_i - \bar{X})^2\], y lo mismo para la desviación estándar: \[\hat{\sigma}=\sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(X_i-\bar{X})^2}\]. Bien, estoy ocultando algo más aquí. En un giro extraño y contraintuitivo, dado que \(\hat{\sigma}^2\) es un estimador insesgado de \(\sigma^2\), se supondría que sacar la raíz cuadrada estaría bien y \(\hat{\ sigma}\) sería un estimador insesgado de σ. ¿Cierto? Extrañamente, no lo es. En realidad, hay un sesgo sutil, pequeño en \(\hat{\sigma}\). Esto es simplemente extraño: \(\hat{\sigma}^2\) es una estimación insesgada de la varianza poblacional \(\sigma^2\) , pero cuando sacas la raíz cuadrada, resulta que \(\hat{\sigma}\) es un estimador sesgado de la desviación estándar de la población σ. Raro, raro, raro, ¿verdad? Entonces, ¿por qué es \(\hat{\sigma}\) sesgada? La respuesta técnica es “porque las transformaciones no lineales (por ejemplo, la raíz cuadrada) no conmutan con la expectativa”, pero eso suena como un galimatías para todos los que no han hecho un curso de estadística matemática. Afortunadamente, a efectos prácticos no importa. El sesgo es pequeño, y en la vida real todo el mundo utiliza \(\hat{\sigma}\) y funciona bien. A veces las matemáticas son simplemente molestas.

8. Esta cita aparece en muchas camisetas y sitios web, e incluso se menciona en algunos artículos académicos (p. ej., http://www.amstat.org/publications/jse/v10n3/friedman.html , pero nunca encontré la fuente original.

9. Matemáticamente, escribimos esto como: \[\mu-(1.96 \times SEM ) \leq \bar{X} \leq \mu + ( 1.96 \times SEM)\] donde el SEM es igual a \(\frac{\sigma}{\sqrt{N}}\) N y podemos estar seguras al 95% de que esto es cierto. Sin embargo, eso no responde a la pregunta que realmente nos interesa. La ecuación anterior nos dice lo que debemos esperar sobre la media muestral dado que sabemos cuáles son los parámetros de la población. Lo que queremos es que funcione al revés. Queremos saber qué debemos creer sobre los parámetros poblacionales, dado que hemos observado una muestra concreta. Sin embargo, no es demasiado difícil hacer esto. Usando un poco de álgebra de secundaria, una forma astuta de reescribir nuestra ecuación es la siguiente: \[\bar{X}-(1.96 \times SEM ) \leq \mu \leq \bar{X}+(1.96 \times SEM ) \] Lo que esto nos dice es que el rango de valores tiene una probabilidad del 95% de contener la media poblacional µ. Nos referimos a este rango como un intervalo de confianza del 95 %, denominado \(CI_{95}\). En resumen, siempre que N sea lo suficientemente grande (lo suficientemente grande par que creamos que la distribución muestral de la media es normal), entonces podemos escribir esto como nuestra fórmula para el intervalo de confianza del 95%: \[CI_{95}= \bar{X} \pm (1,96 \times \frac{\sigma}{\sqrt{N}})\]