9 Prueba de hipótesis

El proceso de inducción consiste en asumir la ley más simple que se pueda armonizar con nuestra experiencia. Este proceso, sin embargo, no tiene fundamento lógico sino sólo psicológico. Está claro que no hay motivos para creer que el curso más simple de los acontecimientos vaya a suceder realmente. Es una hipótesis que el sol saldrá mañana, lo que significa que no sabemos si saldrá. – Ludwig Wittgenstein ¹

En el último capítulo discutí las ideas en las que se basa la estimación, que es una de las dos “grandes ideas” de la estadística inferencial. Ahora es el momento de centrar nuestra atención en la otra gran idea, que es la prueba de hipótesis. En su forma más abstracta, la prueba de hipótesis es realmente una idea muy simple. El investigador tiene una teoría sobre el mundo y quiere determinar si los datos apoyan o no esa teoría. Sin embargo, los detalles son complicados y la mayoría de la gente considera que la teoría de la prueba de hipótesis es la parte más frustrante de la estadística. La estructura del capítulo es la siguiente. En primer lugar, describiré cómo funcionan las prueba de hipótesis con bastante detalle, utilizando un ejemplo sencillo para mostrar cómo se “construye” una prueba de hipótesis. Intentaré no ser demasiado dogmática centrarme en la lógica subyacente del procedimiento de prueba.² Luego, dedicaré un poco de tiempo a hablar sobre los diversos dogmas, reglas y herejías que rodean la teoría de la prueba de hipótesis.

9.1 Una colección de hipótesis

Al final todos sucumbimos a la locura. Para mí, ese día llegará cuando por fin me asciendan a catedrática. Instalada en mi torre de marfil, felizmente protegida por la cátedra, podré por fin despedirme de mis sentidos (por así decirlo) y dedicarme a esa línea de investigación psicológica más improductiva, la búsqueda de la percepción extrasensorial (PES).³

Supongamos que este glorioso día ha llegado. Mi primer estudio es sencillo y consiste en probar si existe la clarividencia. Cada participante se sienta en una mesa y un experimentador le muestra una tarjeta. La tarjeta es negra por un lado y blanca por el otro. El experimentador retira la tarjeta y la coloca sobre una mesa en una habitación contigua. La tarjeta se coloca con el lado negro hacia arriba o el lado blanco hacia arriba de forma totalmente aleatoria, y la aleatorización se produce después de que el experimentador haya salido de la habitación con el participante. Entra un segundo experimentador y le pregunta al participante qué lado de la tarjeta está ahora hacia arriba. Es un experimento de una sola vez. Cada persona ve solo una tarjeta y da solo una respuesta, y en ningún momento el participante está en contacto con alguien que sepa la respuesta correcta. Mi conjunto de datos, por lo tanto, es muy sencillo. He hecho la pregunta a N personas y un número $X$ de ellas ha dado la respuesta correcta. Para concretar, supongamos que he hecho la prueba a $N = 100$ personas y $X = 62$ de ellas han dado la respuesta correcta. Un número sorprendentemente grande, sin duda, pero ¿es lo suficientemente grande como para que pueda afirmar que he encontrado pruebas de la PES? Esta es la situación en la que las pruebas de hipótesis resultan útiles. Sin embargo, antes de hablar de cómo probar hipótesis, debemos tener claro qué entendemos por hipótesis.

9.1.1 Hipótesis de investigación versus hipótesis estadísticas

La primera distinción que debes tener clara es entre hipótesis de investigación e hipótesis estadísticas. En mi estudio sobre la PES, mi objetivo científico general es demostrar que existe la clarividencia. En esta situación, tengo un objetivo de investigación claro: espero descubrir pruebas de la PES. En otras situaciones, podría ser mucho más neutral que eso, por lo que podría decir que mi objetivo de investigación es determinar si existe o no la clarividencia. Independientemente de cómo me presente, lo que quiero decir es que una hipótesis de investigación implica hacer una afirmación científica sustantiva y comprobable. Si eres psicóloga, tus hipótesis de investigación se refieren fundamentalmente a constructos psicológicos. Cualquiera de las siguientes contaría como hipótesis de investigación:

Escuchar música reduce la capacidad de prestar atención a otras cosas. Se trata de una afirmación sobre la relación causal entre dos conceptos psicológicamente significativos (escuchar música y prestar atención a las cosas), por lo que es una hipótesis de investigación perfectamente razonable.
La inteligencia está relacionada con la personalidad. Al igual que la anterior, se trata de una afirmación relacional sobre dos constructos psicológicos (inteligencia y personalidad), pero la afirmación es más débil: correlacional, no causal.
La inteligencia es la velocidad de procesamiento de la información. Esta hipótesis tiene un carácter bastante diferente. En realidad, no es una afirmación relacional en absoluto. Es una afirmación ontológica sobre el carácter fundamental de la inteligencia (y estoy bastante segura de que en realidad es ésta). Normalmente es más fácil pensar en cómo construir experimentos para probar hipótesis de investigación del tipo “¿afecta $X$ a $Y$?” que abordar afirmaciones como “¿qué es $X$?” Y en la práctica, lo que suele ocurrir es que se encuentran formas de probar las afirmaciones relacionales que se derivan de las ontológicas. Por ejemplo, si creo que la inteligencia es la velocidad de procesamiento de la información en el cerebro, mis experimentos consistirán a menudo en buscar relaciones entre medidas de inteligencia y medidas de velocidad. En consecuencia, la mayoría de las preguntas de investigación cotidianas tienden a ser de naturaleza relacional, pero casi siempre están motivadas por preguntas ontológicas más profundas sobre el estado de naturaleza.

Ten en cuenta que en la práctica, mis hipótesis de investigación podrían solaparse mucho. Mi objetivo final en el experimento de PES podría ser probar una afirmación ontológica como “la PES existe”, pero podría restringirme operativamente a una hipótesis más limitada como “algunas personas pueden ‘ver’ objetos de manera clarividente”. Dicho esto, hay algunas cosas que realmente no cuentan como hipótesis de investigación adecuadas en ningún sentido significativo:

El amor es un campo de batalla. Esto es demasiado vago para ser comprobable. Aunque está bien que una hipótesis de investigación tenga cierto grado de vaguedad, tiene que ser posible operacionalizar tus ideas teóricas. Tal vez no soy lo bastante creativa para verlo, pero no veo cómo se puede convertir esto en un diseño de investigación concreto. Si eso es cierto, entonces esta no es una hipótesis de investigación científica, es una canción pop. Eso no significa que no sea interesante. Muchas preguntas profundas que se hacen los humanos entran en esta categoría. Quizá algún día la ciencia sea capaz de construir teorías comprobables sobre el amor, o comprobar si Dios existe, etcétera. Pero ahora mismo no podemos, y yo no apostaría por ver nunca una aproximación científica satisfactoria a ninguna de las dos cosas.
La primera regla del club de la tautología es la primera regla del club de la tautología. No es una afirmación sustantiva de ningún tipo. Es cierta por definición. Ningún estado de la naturaleza concebible podría ser incompatible con esta afirmación. Decimos que se trata de una hipótesis infalsable, y como tal está fuera del dominio de la ciencia. Independientemente de lo que se haga en ciencia, tus afirmaciones deben tener la posibilidad de ser erróneas.
En mi experimento más gente dirá “sí” que “no”. Esto falla como hipótesis de investigación porque es una afirmación sobre el conjunto de datos, no sobre la psicología (a menos, por supuesto, que tu pregunta de investigación real sea si las personas tienen algún tipo de sesgo hacia el “sí”). En realidad, esta hipótesis empieza a parecer más una hipótesis estadística que una hipótesis de investigación.

Como puedes ver, las hipótesis de investigación pueden ser algo complicadas a veces y, en última instancia, son afirmaciones científicas. Las hipótesis estadísticas no son ninguna de estas dos cosas. Las hipótesis estadísticas deben ser precisas y deben corresponder a afirmaciones concretas sobre las características del mecanismo de generación de datos (es decir, la “población”). Aun así, la intención es que las hipótesis estadísticas guarden una relación clara con las hipótesis de investigación sustantivas que te interesan. Por ejemplo, en mi estudio sobre PES, mi hipótesis de investigación es que algunas personas son capaces de ver a través de las paredes o lo que sea. Lo que quiero hacer es “mapear” esto en una afirmación sobre cómo se generaron los datos. Así que vamos a pensar en lo que sería esa afirmación. La cantidad que me interesa dentro del experimento es $P(correcta)$, la probabilidad verdadera pero desconocida con la que los participantes en mi experimento responden la pregunta correctamente. Usemos la letra griega $\theta$ (theta) para referirnos a esta probabilidad. Aquí hay cuatro hipótesis estadísticas diferentes:

Si la PES no existe y si mi experimento está bien diseñado, entonces mis participantes solo están adivinando. Así que debería esperar que acierten la mitad de las veces, y entonces mi hipótesis estadística es que la verdadera probabilidad de elegir correctamente es $\theta=0.5$.
Alternativamente, supongamos que la PES existe y que los participantes pueden ver la tarjeta. Si eso es cierto, la gente obtendrá mejores resultados que el azar y la hipótesis estadística es que $\theta > 0,5$.
Una tercera posibilidad es que la PES exista, pero los colores estén todos invertidos y la gente no se dé cuenta (vale, es una locura, pero nunca se sabe). Si es así, es de esperar que los resultados sean inferiores al azar. Esto correspondería a una hipótesis estadística de que $\theta < 0.5$.
Por último, supongamos que la PES existe pero no tengo idea si la gente ve el color correcto o el incorrecto. En ese caso, la única afirmación que podría hacer sobre los datos sería que la probabilidad de acertar la respuesta correcta no es igual a 0,5. Esto corresponde a la hipótesis estadística de que $\theta \neq 0.5$.

Todos estos son ejemplos legítimos de una hipótesis estadística porque son afirmaciones sobre un parámetro de la población y están relacionados de forma significativa con mi experimento.

Lo que esta discusión deja claro, espero, es que cuando se intenta construir una prueba de hipótesis estadística, el investigador tiene que tener en cuenta dos hipótesis muy distintas. En primer lugar, tiene una hipótesis de investigación (una afirmación sobre la psicología), que corresponde a una hipótesis estadística (una afirmación sobre la población que genera los datos). En mi ejemplo de PES, podrían ser las que se muestran en Table 9.1.

Table 9.1:
Investigación e hipótesis estadísticas
Dani's research hypothesis:	"ESP exists"
Dani's statistical hypothesis:	$ \theta \neq 0.5 $

Y una cosa clave que hay que reconocer es lo siguiente. Una prueba de hipótesis estadística es una prueba de la hipótesis estadística, no de la hipótesis de investigación. Si el estudio está mal diseñado, se rompe el vínculo entre la hipótesis de investigación y la hipótesis estadística. Para poner un ejemplo tonto, supongamos que mi estudio de PES se realizara en una situación en la que el participante pudiera ver realmente la tarjeta reflejada en una ventana. Si eso sucede, podrías encontrar pruebas muy sólidas de que $\theta \neq 0.5$, pero esto no nos diría nada sobre si “la PES existe”.

9.1.2 Hipótesis nulas e hipótesis alternativas

Hasta aquí, todo bien. Tengo una hipótesis de investigación que corresponde a lo que quiero creer sobre el mundo, y puedo mapearla en una hipótesis estadística que corresponde a lo que quiero creer sobre cómo se generaron los datos. Es en este punto donde las cosas se vuelven contraintuitivas para mucha gente. Porque lo que estoy a punto de hacer es inventar una nueva hipótesis estadística (la hipótesis “nula”, $H_0$ ) que corresponde exactamente a lo contrario de lo que quiero creer, y luego centrarme exclusivamente en ella casi en detrimento de lo que realmente me interesa (que ahora se llama la hipótesis “alternativa”, H1). En nuestro ejemplo de PES, la hipótesis nula es que $\theta = 0.5$, ya que eso es lo que esperaríamos si la PES no existiera. Mi esperanza, por supuesto, es que la PES es totalmente real, y por lo tanto la alternativa a esta hipótesis nula es $\theta \neq 0.5$. En esencia, lo que estamos haciendo aquí es dividir los posibles valores de $\theta$ en dos grupos: aquellos valores que realmente espero que no sean ciertos (la nula) y aquellos valores con los que estaría contenta si resultaran ser correctos (la alternativa). Una vez hecho esto, lo importante es reconocer que el objetivo de una prueba de hipótesis no es demostrar que la hipótesis alternativa es (probablemente) cierta. El objetivo es demostrar que la hipótesis nula es (probablemente) falsa. A la mayoría de la gente esto le parece bastante extraño.

según mi experiencia, la mejor manera de pensar en ello es imaginar que una prueba de hipótesis es un juicio penal⁴, el juicio de la hipótesis nula. La hipótesis nula es el acusado, el investigador es el fiscal y la prueba estadística es el juez. Al igual que en un juicio penal, existe la presunción de inocencia. La hipótesis nula se considera cierta a menos que tú, la investigadora, puedas probar más allá de toda duda razonable que es falsa. Eres libre de diseñar tu experimento como quieras (dentro de lo razonable, obviamente) y tu objetivo al hacerlo es maximizar la probabilidad de que los datos generen una condena por el delito de ser falsos. El truco está en que la prueba estadística establece las reglas del juicio y esas reglas están diseñadas para proteger la hipótesis nula, concretamente para garantizar que, si la hipótesis nula es realmente cierta, las posibilidades de una condena falsa están garantizadas para ser bajas. Esto es muy importante. Después de todo, la hipótesis nula no tiene abogado, y dado que el investigador está intentando desesperadamente demostrar que es falsa, alguien tiene que protegerla.

9.2 Dos tipos de errores

Antes de entrar en detalles sobre cómo se construye una prueba estadística, es útil entender la filosofía que hay detrás. Lo he insinuado al señalar la similitud entre una prueba de hipótesis nula y un juicio penal, pero ahora debo ser explícita. Idealmente, nos gustaría construir nuestra prueba de forma que nunca cometiéramos errores. Por desgracia, dado que el mundo está desordenado, esto nunca es posible. A veces simplemente tienes mala suerte. Por ejemplo, supongamos que lanzamos una moneda 10 veces seguidas y sale cara las 10 veces. Eso parece una prueba muy sólida para llegar a la conclusión de que la moneda está sesgada, pero, por supuesto, hay una probabilidad de 1 entre 1024 de que esto ocurriera incluso si la moneda fuera totalmente justa. En otras palabras, en la vida real siempre tenemos que aceptar que existe la posibilidad de que nos hayamos equivocado. En consecuencia, el objetivo de las pruebas de hipótesis estadística no es eliminar los errores, sino minimizarlos.

Llegados a este punto, debemos ser un poco más precisas sobre lo que entendemos por “errores”. En primer lugar, digamos lo obvio. O bien la hipótesis nula es verdadera, o bien es falsa, y nuestra prueba mantendrá la hipótesis nula o la rechazará.⁵ Así que, como ilustra Table 9.2, después de ejecutar la prueba y hacer nuestra elección, podría haber ocurrido una de cuatro cosas:

Table 9.2:
prueba estadística de hipótesis nula (NHST)
	retain $ H_0 $	reject $ H_0 $
$ H_0 $ is true	correct decision	error (type I)
$ H_0 $ is false	error (type II)	correct decision

Por consiguiente, en realidad hay dos tipos de error. Si rechazamos una hipótesis nula que en realidad es cierta, cometemos un error de tipo I. Por otro lado, si mantenemos la hipótesis nula cuando en realidad es falsa, cometemos un error de tipo II.

¿Recuerdas que dije que las pruebas estadísticas eran como un juicio penal? Pues lo decía en serio. Un juicio penal requiere que se demuestre “más allá de toda duda razonable” que el acusado lo hizo. Todas las normas probatorias están (al menos en teoría) diseñadas para garantizar que no haya (casi) ninguna probabilidad de condenar injustamente a un acusado inocente. El juicio está diseñado para proteger los derechos de un acusado, como dijo el famoso jurista inglés William Blackstone, es “mejor que escapen diez culpables a que sufra un inocente”. En otras palabras, un juicio penal no trata de la misma manera los dos tipos de error. Castigar al inocente se considera mucho peor que dejar libre al culpable. Una prueba estadística es más o menos lo mismo. El principio de diseño más importante de la prueba es controlar la probabilidad de un error de tipo I, para mantenerla por debajo de una probabilidad fija. Esta probabilidad, que se denota $\alpha$, se llama nivel de significación de la prueba. Y lo diré de nuevo, porque es fundamental para todo el montaje: se dice que una prueba de hipótesis tiene un nivel de significación $\alpha$ si la tasa de error tipo I no es mayor que $\alpha$.

¿Y qué pasa con la tasa de error tipo II? Bueno, también nos gustaría tenerla bajo control, y denotamos esta probabilidad por $\beta$. Sin embargo, es mucho más común referirse a la potencia de la prueba, que es la probabilidad con la que rechazamos una hipótesis nula cuando realmente es falsa, que es $1 - \beta$. Para que no nos equivoquemos, aquí tenemos de nuevo la misma tabla pero con los números correspondientes añadidos (Table 9.3):

Table 9.3:
prueba estadística de hipótesis nula (NHST) - detalle adicional
	retain $ H_0 $	reject $ H_0 $
$ H_0 $ is true	1-$ \alpha $ (probability of correct retention)	$\alpha$ (type I error rate)
$ H_0 $ is false	$\beta$ (type II error rate)	$1 - \beta$ (power of the test)

Una prueba de hipótesis “potente” es aquella que tiene un valor pequeño de $\beta$, mientras mantiene $\alpha$ fijo en algún nivel (pequeño) deseado. Por convención, los científicos utilizan tres niveles $\alpha$ diferentes: $.05$, $.01$ y $.001$. Fíjate en la asimetría aquí; las pruebas están diseñadas para garantizar que el nivel de $\alpha$ se mantiene bajo, pero no hay ninguna garantía correspondiente con respecto a $\beta$. Sin duda, nos gustaría que la tasa de error de tipo II fuera pequeña y tratamos de diseñar pruebas que la mantengan pequeña, pero esto suele ser secundario frente a la abrumadora necesidad de controlar la tasa de error de tipo I. Como habría dicho Blackstone si fuera estadístico, es “mejor retener 10 hipótesis nulas falsas que rechazar una única verdadera”. Para ser sincera, no sé si estoy de acuerdo con esta filosofía. Hay situaciones en las que creo que tiene sentido y situaciones en las que creo que no, pero eso no viene al caso. Es como se construyen las pruebas.

9.3 Pruebas estadísticas y distribuciones muestrales

Llegados a este punto, tenemos que empezar a hablar en concreto de cómo se construye una prueba de hipótesis. Para ello, volvamos al ejemplo de la PES. Ignoremos los datos reales que obtuvimos, por el momento, y pensemos en la estructura del experimento. Independientemente de cuáles sean los números reales, la forma de los datos es que $X$ de $N$ personas identificaron correctamente el color de la carta oculta. Además, supongamos por el momento que la hipótesis nula es realmente cierta, que la PES no existe y que la probabilidad real de que alguien elija el color correcto es exactamente $\theta = 0,5$. ¿Cómo esperaríamos que fueran los datos? Bueno, obviamente esperaríamos que la proporción de personas que dan la respuesta correcta fuera bastante cercana al $50\%$. O, para expresarlo en términos más matemáticos, diríamos que $\frac{X}{N}$ es aproximadamente $0,5$. Por supuesto, no esperaríamos que esta fracción fuera exactamente $0.5$. Si, por ejemplo, probamos $N = 100$ personas y $X = 53$ de ellas acertaron la pregunta, probablemente nos veríamos obligadas a admitir que los datos son bastante coherentes con la hipótesis nula. Por otro lado, si $X = 99$ de nuestros participantes acertaron la pregunta, estaríamos bastante seguras de que la hipótesis nula es errónea. Del mismo modo, si solo $X = 3$ personas acertaron la respuesta, estaríamos igualmente seguras de que la hipótesis nula era incorrecta. Seamos un poco más técnicas. Tenemos una cantidad $X$ que podemos calcular observando nuestros datos. Tras observar el valor de $X$, decidimos si creemos que la hipótesis nula es correcta o si rechazamos la hipótesis nula a favor de la alternativa. El nombre de esta cosa que calculamos para guiar nuestras decisiones es la prueba estadística.

Una vez elegida la prueba estadística, el siguiente paso es establecer con precisión qué valores de la prueba estadística harían que se rechazara la hipótesis nula y qué valores harían que la mantuviéramos. Para ello, debemos determinar cuál sería la distribución muestral de la prueba estadística si la hipótesis nula fuera realmente cierta (ya hemos hablado de las distribuciones muestrales en Section 8.3.1 ¿Por qué necesitamos esto? Porque esta distribución nos dice exactamente qué valores de X nos llevaría a esperar nuestra hipótesis nula. Y, por tanto, podemos usar esta distribución como una herramienta para evaluar hasta qué punto la hipótesis nula concuerda con nuestros datos.

¿Cómo determinamos realmente la distribución muestral de la prueba estadística? Para muchas pruebas de hipótesis, este paso es bastante complicado, y más adelante en el libro verás que soy un poco evasiva al respecto para algunas de las pruebas (algunas ni yo misma las entiendo). Sin embargo, a veces es muy fácil. Y, afortunadamente para nosotras, nuestro ejemplo PES nos proporciona uno de los casos más fáciles. Nuestro parámetro poblacional $\theta$ es simplemente la probabilidad global de que la gente responda correctamente a la pregunta, y nuestra prueba estadística $X$ es el recuento del número de personas que lo hicieron de una muestra de tamaño N. Ya hemos visto una distribución como esta antes, en Section 7.4, ¡y eso es exactamente lo que describe la distribución binomial! Así que, para usar la notación y la terminología que introduje en esa sección, diríamos que la hipótesis nula predice que $X$ se distribuye binomialmente, lo cual se escribe

\[X \sum Binomial(\theta,N)\]

Dado que la hipótesis nula establece que $\theta = 0.5$ y nuestro experimento tiene $N = 100$ personas, tenemos la distribución muestral que necesitamos. Esta distribución muestral se representa en Figure 9.1. En realidad, no hay sorpresas, la hipótesis nula dice que $X = 50$ es el resultado más probable, y dice que es casi seguro que veamos entre $40$ y $60$ respuestas correctas.

Figure 9.1: La distribución muestral para nuestra prueba estadística $X$ cuando la hipótesis nula es verdadera. Para nuestro escenario PES se trata de una distribución binomial. No es de extrañar, dado que la hipótesis nula dice que la probabilidad de una respuesta correcta es $\theta = .5$, la distribución muestral dice que el valor más probable es 50 (de 100) respuestas correctas. La mayor parte de la masa de probabilidad se encuentra entre 40 y 60

9.4 Tomando decisiones

Bien, estamos muy cerca de terminar. Hemos construido una prueba estadística $(X)$ y la elegimos de tal manera que estamos bastante seguras de que si $X$ está cerca de $\frac{N}{2}$ entonces deberíamos mantener la nula, y si no, debemos rechazarla. La pregunta que queda es la siguiente. ¿Exactamente qué valores de la prueba estadística deberíamos asociar con la hipótesis nula y exactamente qué valores van con la hipótesis alternativa? En mi estudio PES, por ejemplo, he observado un valor de $X = 62$. ¿Qué decisión debo tomar? ¿Debo optar por creer en la hipótesis nula o en la hipótesis alternativa?

9.4.1 Regiones críticas y valores críticos

Para responder a esta pregunta necesitamos introducir el concepto de región crítica para la prueba estadística X. La región crítica de la prueba corresponde a aquellos valores de X que nos llevarían a rechazar la hipótesis nula (razón por la cual la región crítica también se denomina a veces región de rechazo). ¿Cómo encontramos esta región crítica? Consideremos lo que sabemos:

$X$ debe ser muy grande o muy pequeña para rechazar la hipótesis nula
Si la hipótesis nula es verdadera, la distribución muestral de $X$ es $Binomial(0.5, N)$
Si $\alpha = .05$, la región crítica debe cubrir el 5% de esta distribución muestral.

Es importante que comprendas este último punto. La región crítica corresponde a aquellos valores de $X$ para los que rechazaríamos la hipótesis nula, y la distribución muestral en cuestión describe la probabilidad de que obtuviéramos un valor particular de $X$ si la hipótesis nula fuera realmente cierta. Ahora, supongamos que elegimos una región crítica que cubre $20\%$ de la distribución muestral, y supongamos que la hipótesis nula es realmente cierta. ¿Cuál sería la probabilidad de rechazar incorrectamente la nula? La respuesta es, por supuesto, $20\%$. Y, por tanto, habríamos construido una prueba que tuviera un nivel α de $0.2$. Si queremos $\alpha = .05$, la región crítica solo puede cubrir el 5% de la distribución muestral de nuestra prueba estadística.

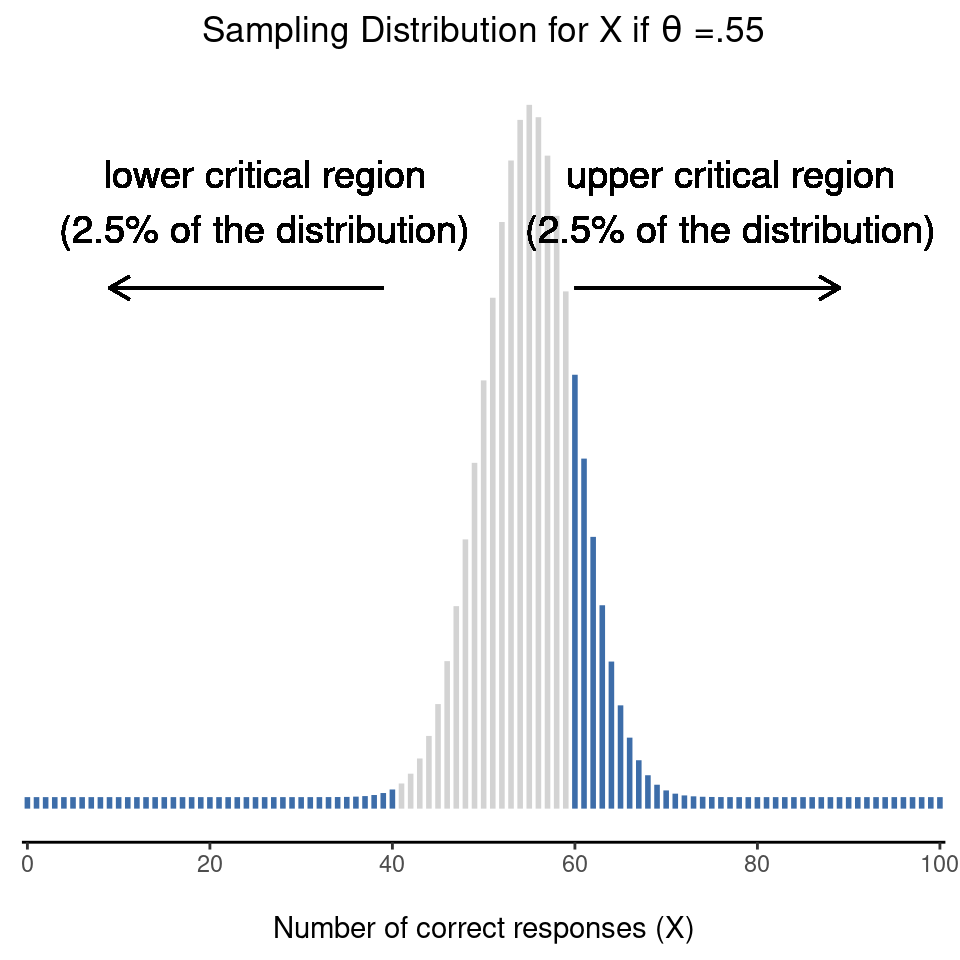
Resulta que esas tres cosas resuelven el problema de forma única. Nuestra región crítica consiste en los valores más extremos, conocidos como las colas de la distribución. Esto se ilustra en Figure 9.2. Si queremos $\alpha = .05$ entonces nuestras regiones críticas corresponden a $X \leq 40$ y $X \geq 60$.⁶ Es decir, si el número de personas que dicen ” verdadero” está entre 41 y 59, entonces deberíamos mantener la hipótesis nula. Si el número está entre $0$ y $40$, o entre $60$ y $100$, debemos rechazar la hipótesis nula. Los números $40$ y $60$ suelen denominarse valores críticos, ya que definen los bordes de la región crítica.

Figure 9.2: La región crítica asociada con la prueba de hipótesis para el estudio PES, para una prueba de hipótesis con un nivel de significación de $\alpha = .05$. El gráfico muestra la distribución muestral de $X$ bajo la hipótesis nula (es decir, igual que Figure 9.1). Las barras grises corresponden a aquellos valores de $X$ para los que mantendríamos la hipótesis nula. Las barras azules (sombreadas más oscuras) muestran la región crítica, aquellos valores de $X$ para los que rechazaríamos la hipótesis nula. Debido a que la hipótesis alternativa es bilateral (es decir, permite tanto $\theta < .5$ como $\theta > .5$, la región crítica cubre ambas colas de la distribución. Para asegurar un nivel de $\alpha$ de $.05 $, debemos asegurarnos de que cada una de las dos regiones abarca $2.5\%$ de la distribución muestral

En este punto, nuestra prueba de hipótesis está prácticamente completa:

Elegimos un nivel α (por ejemplo, $\alpha = .05$);
Obtenemos alguna prueba estadística (por ejemplo, $X$) que haga un buen trabajo (en algún sentido significativo) al comparar $H_0$ con $H_1$;
Calculamos la distribución muestral de la prueba estadística suponiendo que la hipótesis nula es verdadera (en este caso, binomial); y entonces
Calculamos la región crítica que produce un nivel α apropiado (0-40 y 60-100).

Todo lo que tenemos que hacer ahora es calcular el valor de la prueba estadística para los datos reales (por ejemplo, X = 62) y luego compararlo con los valores críticos para tomar nuestra decisión. Dado que 62 es mayor que el valor crítico de 60, rechazaríamos la hipótesis nula. O, dicho de otro modo, decimos que la prueba produjo un resultado estadísticamente significativo.

9.4.2 Una nota sobre la “significación” estadística

Al igual que otras técnicas ocultas de adivinación, el método estadístico tiene una jerga privada deliberadamente concebida para ocultar sus métodos a los no practicantes.
– Atribuido a GO Ashley ⁷

Llegados a este punto, conviene hacer una breve digresión sobre la palabra “significativo”. El concepto de significación estadística es en realidad muy sencillo, pero tiene un nombre muy desafortunado. Si los datos nos permiten rechazar la hipótesis nula, decimos que “el resultado es estadísticamente significativo”, que a menudo se abrevia como “el resultado es significativo”. Esta terminología es bastante antigua y se remonta a una época en la que “significativo” solo significaba algo así como “indicado”, en lugar de su significado moderno, que es mucho más cercano a “importante”. Como resultado, muchos lectores modernos se confunden mucho cuando comienzan a aprender estadística porque piensan que un “resultado significativo” debe ser importante. No significa eso en absoluto. Lo único que significa “estadísticamente significativo” es que los datos nos han permitido rechazar una hipótesis nula. Si el resultado es realmente importante o no en el mundo real es una cuestión muy diferente, y depende de muchas otras cosas.

9.4.3 La diferencia entre pruebas unilaterales y bilaterales

Hay una cosa más que quiero señalar sobre la prueba de hipótesis que acabo de construir. Si nos tomamos un momento para pensar en las hipótesis estadísticas que he estado usando, \[H_0: \theta=0.5\] \[H_1:\theta \neq 0.5\] nos damos cuenta de que la hipótesis alternativa cubre tanto la posibilidad de que $ < .5$ como la posibilidad de que $\theta \> .5.$ Esto tiene sentido si realmente creo que PES podría producir un rendimiento mejor que el azar o un rendimiento peor que el azar (y hay algunas personas que piensas así). En lenguaje estadístico, este es un ejemplo de una prueba bilateral. Se llama así porque la hipótesis alternativa cubre el área a ambos “lados” de la hipótesis nula y, en consecuencia, la región crítica de la prueba cubre ambas colas de la distribución muestral (2.5 % a cada lado si α = .05), como se ilustró anteriormente en Figure 9.2. Sin embargo, esa no es la única posibilidad. Es posible que solo estés dispuesta a creer en PES si produce un rendimiento mejor que el azar. Si es así, entonces mi hipótesis alternativa solo cubriría la posibilidad de que $\theta > .5$, y como consecuencia la hipótesis nula ahora se convierte en \[H_0: \theta \leq 0.5\] \[H_1: \theta > 0.5\] Cuando esto ocurre, tenemos lo que se llama una prueba unilateral y la región crítica solo cubre una cola de la distribución muestral. Esto se ilustra en Figure 9.3.

Figure 9.3: La región crítica para una prueba unilateral. En este caso, la hipótesis alternativa es que $\theta \geq .5$ por lo que solo rechazaríamos la hipótesis nula para valores grandes de $X$. Como consecuencia, la región crítica solo cubre la cola superior de la distribución muestral, concretamente el $5\%$ superior de la distribución. Contrasta esto con la versión bilateral en Figure 9.2

9.5 El valor p de una prueba

En cierto sentido, nuestra prueba de hipótesis está completa. Hemos construido una prueba estadística, calculado su distribución muestral si la hipótesis nula es verdadera y a continuación construido la región crítica para la prueba. Sin embargo, en realidad he omitido el número más importante de todos, el valor p. A este tema nos referimos ahora. Hay dos formas algo diferentes de interpretar el valor p, una propuesta por Sir Ronald Fisher y la otra por Jerzy Neyman. Ambas versiones son legítimas, aunque reflejan formas muy diferentes de pensar sobre las pruebas de hipótesis. La mayoría de los libros de texto introductorios tienden a dar solo la versión de Fisher, pero creo que es una lástima. En mi opinión, la versión de Neyman es más limpia y en realidad refleja mejor la lógica de la prueba de hipótesis nula. Sin embargo, puede que no estés de acuerdo, así que he incluido ambas. Empezaré con la versión de Neyman.

9.5.1 Una visión más suave de la toma de decisiones

Un problema con el procedimiento de prueba de hipótesis que he descrito es que no distingue entre un resultado que es “apenas significativo” y los que son “altamente significativos”. Por ejemplo, en mi estudio de PES, los datos que obtuve apenas cayeron dentro de la región crítica, por lo que obtuve un efecto significativo, pero por muy poco. Por el contrario, supongamos que hubiera realizado un estudio en el que $X = 97$ de mis $N = 100$ participantes hubieran acertado la respuesta. Obviamente, esto también sería significativo, pero con un margen mucho mayor, por lo que no habría ambigüedad al respecto. El procedimiento que ya he descrito no distingue entre ambos. Si adopto la convención estándar de permitir $\alpha = .05$ como tasa de error Tipo I aceptable, entonces ambos resultados son significativos.

Aquí es donde el valor p resulta útil. Para entender cómo funciona, supongamos que realizamos muchas pruebas de hipótesis en el mismo conjunto de datos, pero con un valor diferente de α en cada caso. Cuando hacemos eso para mis datos de PES originales, lo que obtendríamos es algo como Table 9.4.

Table 9.4:
Rechazo de la hipótesis nula a diferentes niveles de alfa
Value of $ \alpha $	0.05	0.04	0.03	0.02	0.01
Reject the null?	Yes	Yes	Yes	No	No

Cuando probamos los datos PES ($X = 62$ éxitos de $N = 100$ observaciones), usando $\alpha$ niveles de $.03$ y superiores, siempre nos encontramos rechazando la hipótesis nula. Para niveles de $\alpha$ de $.02$ e inferiores, siempre terminamos manteniendo la hipótesis nula. Por lo tanto, en algún lugar entre $.02$ y $.03$ debe haber un valor más pequeño que $\alpha$ que nos permita rechazar la hipótesis nula para estos datos. Este es el valor de $p$. Resulta que los datos PES tienen $p = .021$. En resumen, $p$ se define como la tasa de error Tipo I más pequeña ($\alpha$) que debemos estar dispuestas a tolerar si queremos rechazar la hipótesis nula.

Si resulta que p describe una tasa de error que te parece intolerable, entonces debes mantener la hipótesis nula. Si te sientes cómoda con una tasa de error igual a $p$, entonces está bien rechazar la hipótesis nula a favor de tu alternativa preferida.

En efecto, $p$ es un resumen de todas las posibles pruebas de hipótesis que podrías haber realizado, tomadas a través de todos los valores posibles de α. Y como consecuencia tiene el efecto de “suavizar” nuestro proceso de decisión. Para aquellas pruebas en las que p ď α habría rechazado la hipótesis nula, mientras que para aquellas pruebas en las que p ą α habría mantenido la nula. En mi estudio PES obtuve $X = 62$ y como consecuencia terminé con $p = .021$. Así que la tasa de error que debo tolerar es de $2.1\%$. Por el contrario, supongamos que mi experimento arrojó $X = 97$. ¿Qué sucede con mi valor p ahora? Esta vez se ha reducido a $p = 1.36$ x $10^{-25}$, que es una tasa de error de Tipo I minúscula, minúscula⁸. En este segundo caso, podrías rechazar la hipótesis nula con mucha más confianza, porque solo tengo que estar “dispuesta” a tolerar una tasa de error tipo I de aproximadamente $ 1 $ en $ 10 $ billones de billones para justificar mi decisión de rechazar.

9.5.2 La probabilidad de datos extremos

La segunda definición del valor p proviene de Sir Ronald Fisher, y en realidad es esta la que suele aparecer en la mayoría de los libros de texto de introducción a la estadística. ¿Te das cuenta de que, cuando construí la región crítica, correspondía a las colas (es decir, valores extremos) de la distribución muestral? Eso no es una coincidencia, casi todas las pruebas “buenas” tienen esta característica (buenas en el sentido de minimizar nuestra tasa de error tipo II, $\beta$). La razón es que una buena región crítica casi siempre corresponde a aquellos valores de la prueba estadística que es menos probable que se observen si la hipótesis nula es cierta. Si esta regla es cierta, podemos definir el valor p como la probabilidad de que hubiéramos observado una prueba estadística que sea al menos tan extrema como la que realmente obtuvimos. En otras palabras, si los datos son extremadamente inverosímiles según la hipótesis nula, entonces es probable que la hipótesis nula sea errónea.

9.5.3 Un error común

De acuerdo, puedes ver que hay dos formas bastante diferentes pero legítimas de interpretar el valor $p$, una basada en el enfoque de Neyman para la prueba de hipótesis y la otra basada en el de Fisher. Desgraciadamente, hay una tercera explicación que la gente da a veces, especialmente cuando están aprendiendo estadística por primera vez, y es absoluta y completamente incorrecta. Este enfoque erróneo consiste en referirse al valor de $p$ como “la probabilidad de que la hipótesis nula sea verdadera”. Es una forma de pensar intuitivamente atractiva, pero errónea en dos aspectos clave. En primer lugar, la prueba de hipótesis nula es una herramienta frecuentista y el enfoque frecuentista de la probabilidad no permite asignar probabilidades a la hipótesis nula. Según esta visión de la probabilidad, la hipótesis nula o es cierta o no lo es, no puede tener un “$5\%$ de probabilidad” de ser cierta. En segundo lugar, incluso dentro del enfoque bayesiano, que sí permite asignar probabilidades a las hipótesis, el valor de p no correspondería a la probabilidad de que la nula sea cierta. Esta interpretación es totalmente incoherente con las matemáticas de cómo se calcula el valor p. Dicho sin rodeos, a pesar del atractivo intuitivo de pensar así, no hay justificación para interpretar un valor $p$ de esta manera. No lo hagas nunca.

9.6 Informar los resultados de una prueba de hipótesis

Cuando se escriben los resultados de una prueba de hipótesis, suele haber varios elementos que hay que informar, pero varían bastante de una prueba a otra. A lo largo del resto del libro, dedicaré algo de tiempo a hablar sobre cómo informar de los resultados de diferentes pruebas (consulta Section 10.1.9 para ver un ejemplo especialmente detallado, para que puedas hacerte una idea de cómo se hace normalmente). Sin embargo, independientemente de la prueba que estés haciendo, lo único que siempre tienes que hacer es decir algo sobre el valor de $p$ y si el resultado fue significativo o no.

El hecho de tener que hacer esto no es sorprendente, es el objetivo de la prueba. Lo que puede sorprender es que haya cierta controversia sobre cómo hacerlo exactamente. Dejando a un lado a las personas que están completamente en desacuerdo con todo el marco en el que se basa la prueba de hipótesis nula, existe cierta tensión sobre si se debe informar o no el valor exacto de $p$ que se ha obtenido, o si sólo se debe indicar que $p < \alpha$ para un nivel de significación que se ha elegido de antemano (por ejemplo, $p < .05$).

9.6.1 La cuestión

Para ver por qué esto es un problema, la clave es reconocer que los valores p son terriblemente convenientes. En la práctica, el hecho de que podamos calcular el valor p significa que en realidad no tenemos que especificar ningún nivel $\alpha$ para realizar la prueba. En su lugar, lo que puedes hacer es calcular su valor p e interpretarlo directamente. Si obtienes $p = 0,062$, significa que tendrías que estar dispuesta a tolerar una tasa de error de tipo I de $6,2\%$ para justificar el rechazo de la hipótesis nula. Si tú personalmente encuentras $6.2\%$ intolerable entonces retienes la hipótesis nula. Por lo tanto, se argumenta, ¿por qué no nos limitamos a comunicar el valor real de $p$ y dejamos que el lector decida por sí mismo cuál es la tasa de error de Tipo I aceptable? Este enfoque tiene la gran ventaja de “suavizar” el proceso de toma de decisiones. De hecho, si aceptas la definición de Neyman del valor p, ese es el punto central del valor p. Ya no tenemos un nivel de significación fijo de $\alpha = .05$ como una línea brillante que separa las decisiones de “aceptar” de las de “rechazar”, y esto elimina el problema bastante patológico de verse obligado a tratar $p = .051$ de una manera fundamentalmente diferente a $p = .049$.

Esta flexibilidad es a la vez una ventaja y un inconveniente del valor $p$. La razón por la que a mucha gente no le gusta la idea de comunicar un valor $p$ exacto es que le da demasiada libertad al investigador. En particular, le permite cambiar de opinión sobre la tolerancia de error que está dispuesto a tolerar después de ver los datos. Por ejemplo, consideremos mi experimento PES. Supongamos que realicé mi prueba y terminé con un valor de $p$ de $.09$. ¿Debo aceptar o rechazar? Para ser sincera, todavía no me he molestado en pensar qué nivel de error Tipo I estoy “realmente” dispuesta a aceptar. No tengo una opinión sobre ese tema. Pero sí tengo una opinión sobre si la PES existe o no, y definitivamente tengo una opinión sobre si mi investigación debería publicarse en una revista científica de prestigio. Y sorprendentemente, ahora que he mirado los datos, estoy empezando a pensar que una tasa de error de $9\%$ no es tan mala, especialmente cuando se compara con lo molesto que sería tener que admitirle al mundo que mi experimento ha fracasado. Así que, para evitar que parezca que lo inventé a posteriori, ahora digo que mi $\alpha$ es .1, con el argumento de que una tasa de error tipo I de $10\%$ no es tan mala y en ese nivel mi prueba es significativa! Yo gano.

En otras palabras, lo que me preocupa es que aunque tenga las mejores intenciones y sea la persona más honesta, la tentación de “matizar” las cosas aquí y allá es muy, muy fuerte. Como puede atestiguar cualquiera que haya realizado un experimento alguna vez, es un proceso largo y difícil y, a menudo, te apegas mucho a tus hipótesis. Es difícil dejarlo ir y admitir que el experimento no encontró lo que querías que encontrara. Y ese es el peligro. Si usamos el valor p “en bruto”, la gente empezará a interpretar los datos en términos de lo que quieren creer, no de lo que los datos dicen en realidad y, si permitimos eso, ¿por qué nos molestamos en hacer ciencia? ? ¿Por qué no dejar que todo el mundo crea lo que quiera sobre cualquier cosa, independientemente de los hechos? Vale, eso es un poco extremo, pero de ahí viene la preocupación. Según este punto de vista, realmente hay que especificar el valor $\alpha$ de antemano y luego solo informar de si la prueba fue significativa o no. Es la única manera de mantenernos honestos.

Table 9.5:
Traducciones típicas de los niveles del valor p
Usual notation	Signif. stars	English translation	The null is...
p > .05		The test wasn't significant	Retained
p < .05	*	The test was significant at $ \alpha $ = .05 but not at $ \alpha $ = .01 or $ \alpha $ = .001.	Rejected
p < .01	**	The test was significant at $ \alpha $ = .05 and $ \alpha $ = .01 but not at $ \alpha $ = .001.	Rejected
p < .001	***	The test was significant at all levels	Rejected

9.6.2 Dos soluciones propuestas

En la práctica, es bastante raro que un investigador especifique un único nivel α de antemano. En su lugar, la convención es que los científicos se basen en tres niveles de significación estándar: $.05$, $.01$ y $.001$. Al comunicar los resultados, se indica cuál de estos niveles de significación (si es que hay alguno) permite rechazar la hipótesis nula. Esto se resume en Table 9.5. Esto nos permite suavizar un poco la regla de decisión, ya que $p < .01$ implica que los datos cumplen con un estándar probatorio más estricto que $p < .05$. Sin embargo, dado que estos niveles se fijan de antemano por convención, se evita que la gente elija su nivel α después de ver los datos.

Sin embargo, mucha gente todavía prefiere comunicar valores de p exactos. Para muchas personas, la ventaja de permitir que el lector tome sus propias decisiones sobre cómo interpretar p = 0,06 supera cualquier desventaja. Sin embargo, en la práctica, incluso entre aquellos investigadores que prefieren valores de p exactos, es bastante común escribir $p < .001$ en lugar de informar un valor exacto para p pequeño. Esto se debe en parte a que una gran cantidad de software en realidad no imprime el valor p cuando es tan pequeño (p. ej., SPSS solo escribe $p = .000$ siempre que $p < .001$), y en parte porque un valor muy pequeño de p puede ser engañoso. La mente humana ve un número como .0000000001 y es difícil suprimir la sensación visceral de que las pruebas a favor de la hipótesis alternativa son casi seguras. En la práctica, sin embargo, esto suele ser erróneo. La vida es algo grande, desordenado y complicado, y todas las pruebas estadísticas que se han inventado se basan en simplificaciones, aproximaciones y suposiciones. Como consecuencia, probablemente no sea razonable salir de ningún análisis estadístico con una sensación de confianza mayor de la que implica $p < .001$. En otras palabras, $p < .001$ es en realidad un código para “en lo que respecta a esta prueba, las pruebas son abrumadoras”.

A la luz de todo esto, es posible que te preguntes qué debes hacer exactamente. Hay bastantes consejos contradictorios sobre el tema, con algunas personas que sostienen que debes informar el valor p exacto y otras que debes usar el enfoque escalonado ilustrado en Table 9.1. Como resultado, el mejor consejo que puedo dar es sugerir que mires los artículos/informes escritos en tu campo y veas cuál parece ser la convención. Si no parece haber ningún patrón coherente, utiliza el método que prefieras.

9.7 Ejecutando la prueba de hipótesis en la práctica

Llegados a este punto, algunas os estaréis preguntando si se trata de una prueba de hipótesis “real” o solo de un ejemplo de juguete que me he inventado. Es real. En la discusión anterior construí la prueba a partir de los primeros principios, pensando que era el problema más simple que podrías encontrarte en la vida real. Sin embargo, esta prueba ya existe. Se llama prueba binomial, y jamovi la implementa como uno de los análisis estadísticos disponibles cuando pulsas el botón ‘Frecuencias’. Para probar la hipótesis nula de que la probabilidad de respuesta es la mitad de $p = .5$,⁹ y usando datos en los que $x =62$ de $n = 100$ personas dieron la respuesta correcta respuesta, disponible en el archivo de datos binomialtest.omv, obtenemos los resultados que se muestran en Figure 9.4.

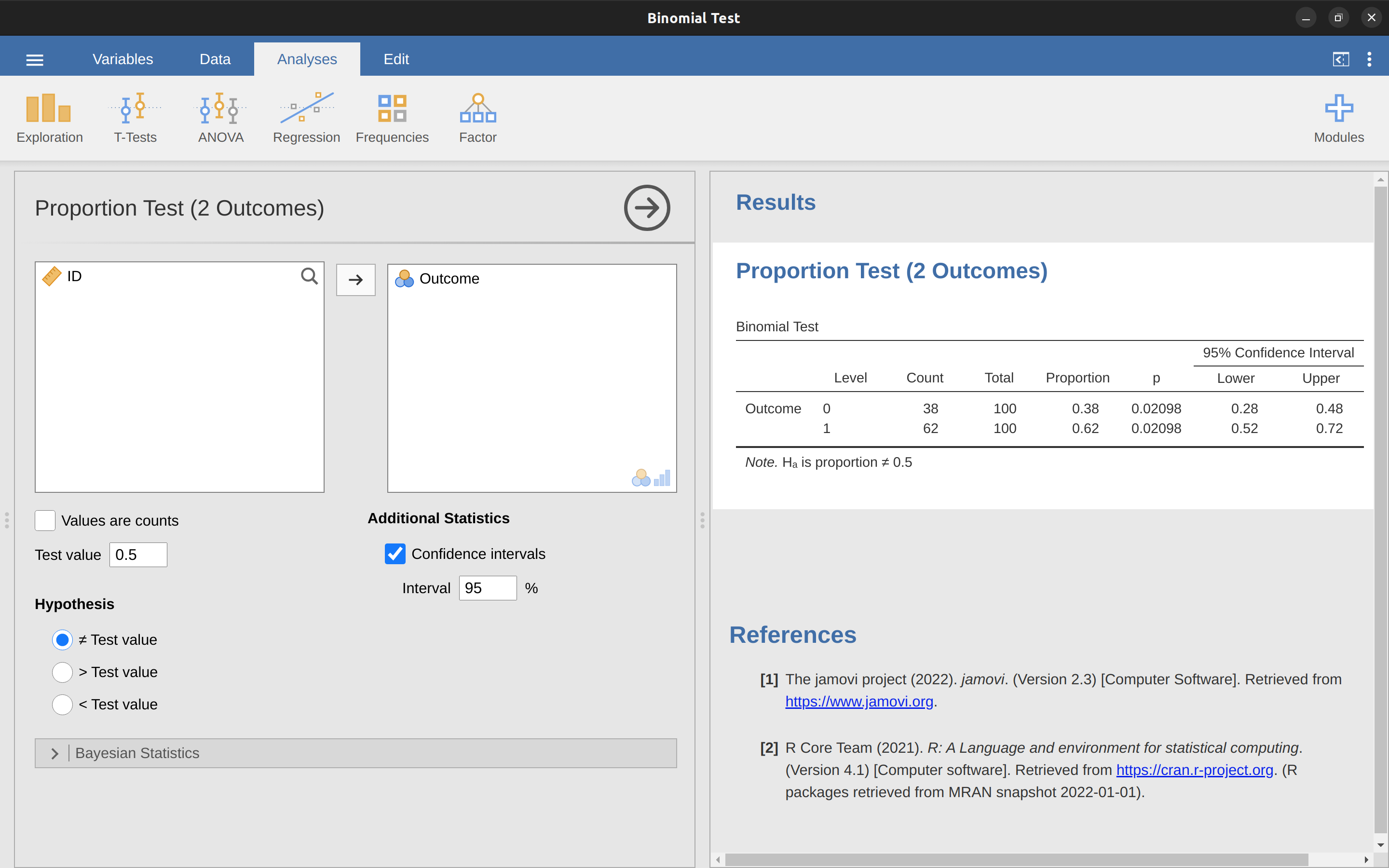
Figure 9.4: análisis de prueba binomial y resultados en jamovi

En este momento, esta salida te parece bastante desconocida, pero puedes ver que te está diciendo más o menos las cosas correctas. En concreto, el valor p de $0,02$ es menor que la elección habitual de $\alpha = 0,05$, por lo que puedes rechazar la hipótesis nula. Hablaremos mucho más sobre cómo leer este tipo de salida a medida que avancemos, y después de un tiempo, con suerte, lo encontrarás bastante fácil de leer y comprender.

9.8 Tamaño del efecto, tamaño de la muestra y potencia

En secciones anteriores, he hecho hincapié en el hecho de que el principal principio de diseño que subyace a las pruebas de hipótesis estadísticas es que intentamos controlar nuestra tasa de error Tipo I. Cuando fijamos $\alpha = .05$ estamos intentando asegurarnos que solo $5\%$ de las hipótesis nulas verdaderas se rechacen incorrectamente. Sin embargo, esto no significa que no nos importen los errores de tipo II. De hecho, desde la perspectiva del investigador, el error de no rechazar la nula cuando en realidad es falsa es extremadamente molesto. Teniendo eso en cuenta, un objetivo secundario de las pruebas de hipótesis es tratar de minimizar $\beta$, la tasa de error de Tipo II, aunque normalmente no hablamos en términos de minimizar los errores de Tipo II. En su lugar, hablamos de maximizar la potencia de la prueba. Dado que la potencia se define como $1 - \beta$, es lo mismo.

9.8.1 La función de potencia

Figure 9.5: Distribución muestral bajo la hipótesis alternativa para un valor de parámetro poblacional de $\theta = 0.55$. Una proporción razonable de la distribución se encuentra en la región de rechazo.

Pensemos un momento en qué es realmente un error de tipo II. Un error de tipo II se produce cuando la hipótesis alternativa es verdadera, pero sin embargo no somos capaces de rechazar la hipótesis nula. Lo ideal sería poder calcular un único número $\beta$ que nos indicara la tasa de error de Tipo II, de la misma manera que podemos establecer $\alpha = .05$ para la tasa de error de Tipo I. Desafortunadamente, esto es mucho más complicado. Para ver esto, observa que en mi estudio PES la hipótesis alternativa en realidad corresponde a un montón de posibles valores de $\theta$. De hecho, la hipótesis alternativa corresponde a cada valor de $\theta$ excepto 0,5. Supongamos que la probabilidad real de que alguien elija la respuesta correcta es del 55% (es decir, $\theta = .55$). Si es así, entonces la verdadera distribución muestral para $X$ no es la misma que predice la hipótesis nula, ya que el valor más probable para $X$ ahora es $55$ de 100. No solo eso, toda la distribución muestral se ha desplazado, como se muestra en Figure 9.5. Las regiones críticas, por supuesto, no cambian. Por definición, las regiones críticas se basan en lo que predice la hipótesis nula. Lo que vemos en esta figura es el hecho de que cuando la hipótesis nula es errónea, una proporción mucho mayor de la distribución muestral cae en la región crítica. Y, por supuesto, eso es lo que debería suceder. ¡La probabilidad de rechazar la hipótesis nula es mayor cuando la hipótesis nula es realmente falsa! Sin embargo $\theta = .55$ no es la única posibilidad consistente con la hipótesis alternativa. Supongamos que el verdadero valor de $\theta$ es en realidad $0,7$. ¿Qué sucede con la distribución muestral cuando esto ocurre? La respuesta, que se muestra en Figure 9.6, es que casi la totalidad de la distribución muestral ahora se ha movido a la región crítica. Por tanto, si $\theta = 0,7$, la probabilidad de que rechacemos correctamente la hipótesis nula (es decir, la potencia de la prueba) es mucho mayor que si $\theta = 0,55$. En resumen, aunque $\theta = .55$ y $\theta = .70$ forman parte de la hipótesis alternativa, la tasa de error de Tipo II es diferente.

Figure 9.6: Distribución muestral bajo la hipótesis *alternativa* para un valor del parámetro poblacional de $\theta = 0.70$. Casi toda la distribución se encuentra en la región de rechazo.

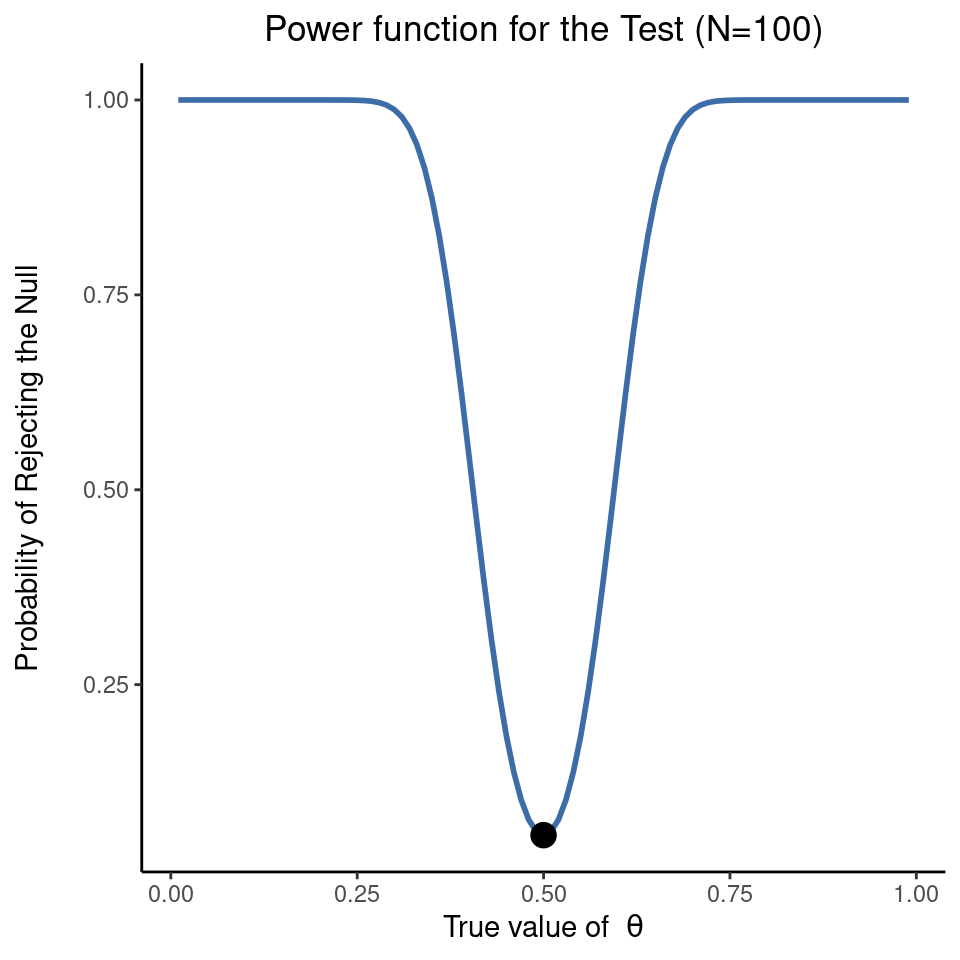
Lo que todo esto significa es que la potencia de una prueba (es decir, $1 - \beta$) depende del verdadero valor de $\theta$. Para ilustrar esto, he calculado la probabilidad esperada de rechazar la hipótesis nula para todos los valores de $\theta$ y la he representado en Figure 9.7. Este gráfico describe lo que normalmente se denomina función de potencia de la prueba. Es un buen resumen de lo buena que es la prueba, porque en realidad nos dice la potencia $(1 - \beta$) para todos los valores posibles de $\theta$. Como se puede ver, cuando el valor verdadero de $\theta$ está muy cerca de $0,5$, la potencia de la prueba cae bruscamente, pero cuando está más lejos, la potencia es grande.

Figure 9.7: La probabilidad de que rechacemos la hipótesis nula, representada como una función del valor verdadero de $\theta$. Obviamente, la prueba es más poderosa (mayor probabilidad de rechazo correcto) si el valor verdadero de $\theta$ es muy diferente del valor que especifica la hipótesis nula (es decir, $\theta = .5$). Observa que cuando $\theta$ en realidad es igual a $.5$ (representado como un punto negro), la hipótesis nula es de hecho verdadera y rechazar la hipótesis nula en este caso sería un error de Tipo I

9.8.2 La función de potencia

Dado que todos los modelos son erróneos, el científico debe estar alerta a lo que es erróneo de manera importante. No es apropiado preocuparse por los ratones cuando hay tigres en el exterior
- Caja de George (Box 1976, p. 792)

El gráfico que se muestra en Figure 9.7 refleja un aspecto básico de las pruebas de hipótesis. Si el estado real del mundo es muy diferente de lo que predice la hipótesis nula, la potencia será muy alta, pero si el estado real del mundo es similar a la hipótesis nula (pero no idéntico), la potencia de la prueba será muy baja. Por lo tanto, es útil poder tener alguna forma de cuantificar lo “similar” que es el verdadero estado del mundo a la hipótesis nula. Un estadístico que hace esto se llama medida del tamaño del efecto (p. ej., Cohen (1988); Ellis (2010)). El tamaño del efecto se define de forma ligeramente diferente en diferentes contextos (por lo que esta sección solo habla en términos generales), pero la idea cualitativa que intenta captar es siempre la misma (ver, por ejemplo, Table 9.6). ¿Cuán grande es la diferencia entre los parámetros poblacionales verdaderos y los valores de los parámetros asumidos por la hipótesis nula? En nuestro ejemplo PES, si dejamos que $\theta_0 = 0.5$ denote el valor asumido por la hipótesis nula y dejamos que $\theta$ denote el valor verdadero, entonces una medida simple del tamaño del efecto podría ser algo así como la diferencia entre el valor verdadero y el nulo (es decir, $\theta - \theta_0$), o posiblemente solo la magnitud de esta diferencia, $abs(\theta - \theta_0)$.

Table 9.6:
Una guía básica para entender la relación entre la significación estadística y los tamaños del efecto. Básicamente, si no se obtiene un resultado significativo, el tamaño del efecto carece de sentido porque no hay pruebas de que sea real. Por otro lado, si se obtiene un efecto significativo pero el tamaño del efecto es pequeño, es muy probable que el resultado (aunque sea real) no sea tan interesante. Sin embargo, esta guía es muy rudimentaria. Depende mucho de lo que se esté estudiando exactamente. Los pequeños efectos pueden tener una enorme importancia práctica en algunas situaciones. Así que no te tomes esta tabla demasiado en serio. Como mucho, es una guía aproximada.
	big effect size	small effect size
significant result	difference is real, and of practical importance	difference is real, but might not be interesting
non-significant result	no effect observed	no effect observed

¿Por qué calcular el tamaño del efecto? Supongamos que has realizado el experimento, has recogido los datos y has obtenido un efecto significativo al realizar la prueba de hipótesis. ¿No basta con decir que se ha obtenido un efecto significativo? ¿Seguro que ese es el objetivo de las pruebas de hipótesis? Bueno, más o menos. Sí, el objetivo de hacer una prueba de hipótesis es intentar demostrar que la hipótesis nula es errónea, pero eso no es lo único que nos interesa. Si la hipótesis nula afirmaba que $\theta = .5$ y demostramos que es errónea, en realidad sólo hemos contado la mitad de la historia. Rechazar la hipótesis nula implica que creemos que $\theta \neq .5$, pero hay una gran diferencia entre $\theta = .51$ y $\theta = .8$. Si encontramos que $\theta = .8$, entonces no solo descubrimos que la hipótesis nula es errónea, sino que parece ser muy errónea. Por otro lado, supongamos que hemos rechazado con éxito la hipótesis nula, pero parece que el verdadero valor de $\theta$ es solo 0,51 (esto solo sería posible con un estudio muy grande). Claro que la hipótesis nula es errónea, pero no está nada claro que nos importe porque el tamaño del efecto es muy pequeño. En el contexto de mi estudio sobre la percepción extrasensorial, es posible que sí nos importe, ya que cualquier demostración de poderes psíquicos reales sería muy interesante¹⁰, pero en otros contextos, una diferencia de $1\%$ generalmente no es muy interesante, aunque sea una diferencia real. Por ejemplo, supongamos que estamos estudiando las diferencias en los resultados de los exámenes de la escuela secundaria entre hombres y mujeres y resulta que los resultados de las mujeres son $1\%$ más altas en promedio que los de los hombres. Si tengo datos de miles de estudiantes, es casi seguro que esta diferencia será estadísticamente significativa, pero independientemente de lo pequeño que sea el valor p, simplemente no es muy interesante. Difícilmente querrías ir por ahí proclamando una crisis en la educación de los chicos basándote en una diferencia tan pequeña, ¿verdad? Por este motivo cada vez es más habitual (lenta, pero inexorablemente) comunicar algún tipo de medida estándar del tamaño del efecto junto con los resultados de la prueba de hipótesis. La prueba de hipótesis en sí te dice si debes creer que el efecto que has observado es real (es decir, que no se debe al azar), mientras que el tamaño del efecto te dice si debes preocuparte o no.

9.8.3 Aumentando la potencia de tu estudio

No es de extrañar que los científicos estén obsesionados con maximizar la potencia de sus experimentos. Queremos que nuestros experimentos funcionen y, por tanto, maximizar la probabilidad de rechazar la hipótesis nula si es falsa (y por supuesto, por lo general, queremos creer que es falsa). Como hemos visto, un factor que influye en la potencia es el tamaño del efecto. Así que lo primero que puedes hacer para aumentar tu potencia es aumentar el tamaño del efecto. En la práctica, esto significa que hay que diseñar el estudio de forma que aumente el tamaño del efecto. Por ejemplo, en mi estudio sobre la percepción extrasensorial podría creer que los poderes psíquicos funcionan mejor en una habitación tranquila y oscura con menos distracciones que nublen la mente. Por lo tanto, trataría de realizar mis experimentos en un entorno así. Si puedo reforzar de algún modo las capacidades de PES de las personas, entonces el valor real de $\theta$ aumentará ¹¹ y, por tanto, el tamaño de mi efecto será mayor. En resumen, un diseño experimental inteligente es una forma de aumentar la potencia, ya que puede alterar el tamaño del efecto.

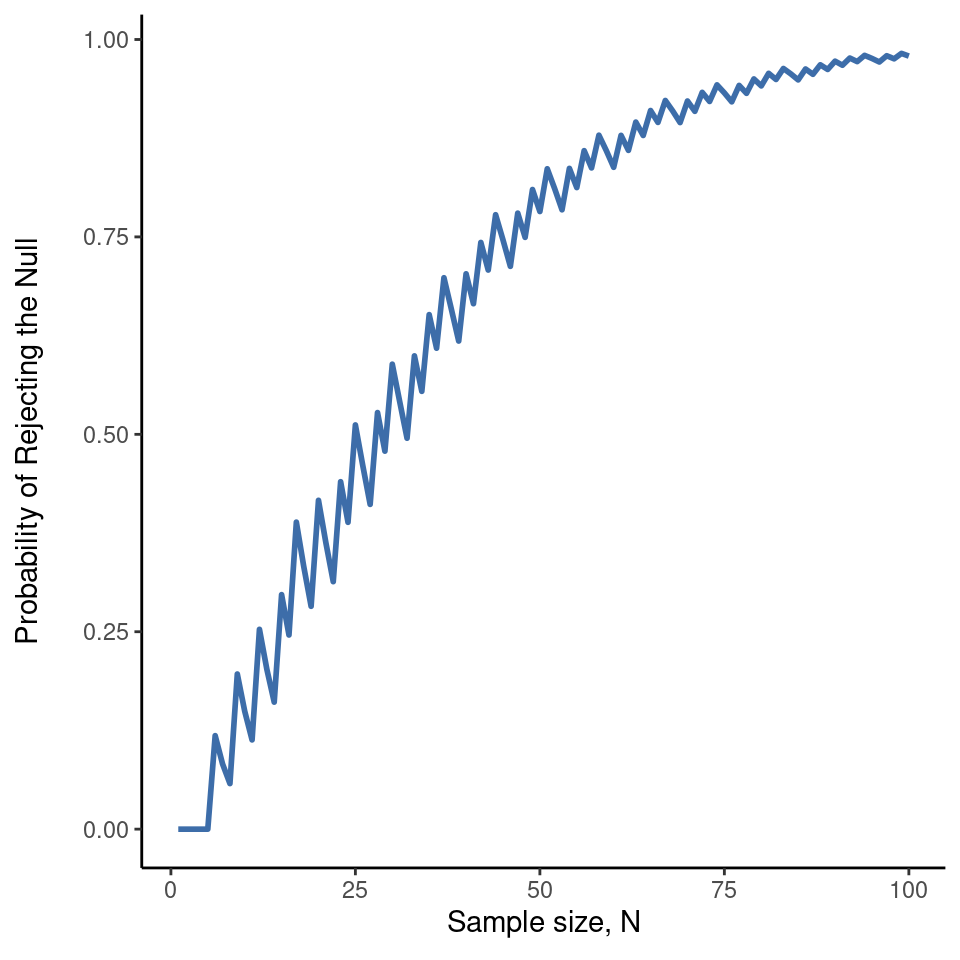
Por desgracia, a menudo ocurre que incluso con el mejor de los diseños experimentales sólo se obtiene un efecto pequeño. Tal vez, por ejemplo, la PES exista realmente , pero incluso en las mejores condiciones es muy, muy débil. En esas circunstancias, lo mejor para aumentar la potencia es aumentar el tamaño de la muestra. En general, cuantas más observaciones tengas disponibles, más probable es que puedas discriminar entre dos hipótesis. Si realizara mi experimento de PES con 10 participantes y 7 de ellos adivinaron correctamente el color de la carta oculta, no estarías muy impresionada. Pero si lo realizara con 10.000 participantes, y 7.000 de ellos acertaran la respuesta, sería mucho más probable que pensaras que había descubierto algo. En otras palabras, la potencia aumenta con el tamaño de la muestra. Esto se ilustra en Figure 9.8, que muestra la potencia de la prueba para un parámetro verdadero de $\theta = 0.7$ para todos los tamaños de muestra $N$ desde $1$ hasta $100$, donde asumo que la hipótesis nula predice que $\theta_0 = 0.5$.

Figure 9.8: La potencia de nuestra prueba en función del tamaño de la muestra $N$. En este caso, el valor verdadero de $\theta$ es 0,7 pero la hipótesis nula es que $\theta = 0,5$. En general, $N$ más grande significa mayor potencia. (Los pequeños zig-zags en esta función se producen debido a algunas interacciones extrañas entre $\theta$, $\alpha$ y el hecho de que la distribución binomial es discreta, no importa para ningún propósito serio)

Dado que la potencia es importante, siempre que te plantees realizar un experimento, sería bastante útil saber cuánta potencia es probable que tengas. Nunca se puede saber con seguridad, ya que es imposible conocer el tamaño del efecto real. Sin embargo, a menudo (bueno, a veces) es posible adivinar cuál debería ser. Si es así, puedes adivinar qué tamaño de muestra necesitas. Esta idea se llama análisis de potencia, y si es posible hacerlo, resulta muy útil. Puede decirte algo sobre si tienes suficiente tiempo o dinero para poder llevar a cabo el experimento con éxito. Cada vez es más frecuente ver a gente que defiende que el análisis de potencia debería ser una parte obligatoria del diseño experimental, por lo que merece la pena conocerlo. Sin embargo, no hablo del análisis de potencia en este libro. Esto es en parte por una razón aburrida y en parte por una razón sustantiva. La razón aburrida es que todavía no he tenido tiempo de escribir sobre el análisis de potencia. La sustantiva es que todavía desconfío un poco del análisis de potencia. Hablando como investigadora, muy rara vez me he encontrado en situación de poder hacer uno. O bien (a) mi experimento es un poco atípico y no sé cómo definir el tamaño del efecto correctamente, o (b) literalmente tengo tan poca idea sobre cuál será el tamaño del efecto que no sabría cómo interpretar las respuestas. No solo eso, después de extensas conversaciones con alguien que se gana la vida haciendo consultoría estadística (mi esposa, por cierto), no puedo evitar darme cuenta de que en la práctica, la única vez que alguien le pide un análisis de potencia es cuando está ayudando a alguien a escribir una solicitud de subvención. En otras palabras, la única vez que un científico parece querer un análisis de potencia en la vida real es cuando se ve obligados a hacerlo por un proceso burocrático. No forma parte del trabajo diario de nadie. En resumen, siempre he sido de la opinión de que, aunque la potencia es un concepto importante, el análisis de potencia no es tan útil como la gente lo hace parecer, excepto en los raros casos en los que (a) alguien ha descubierto cómo calcular la potencia para tu diseño experimental real y (b) tienes una idea bastante buena de cuál es probable que sea el tamaño del efecto.¹² Tal vez otras personas hayan tenido mejores experiencias que yo, pero personalmente nunca he estado en una situación en la que tanto (a) como (b) fueran ciertas. Puede que en el futuro me convenzan de lo contrario, y probablemente una versión futura de este libro incluya una discusión más detallada del análisis de potencia, pero por ahora esto es todo lo que puedo decir sobre el tema.

9.9 Algunas cuestiones a tener en cuenta

Lo que te he descrito en este capítulo es el marco ortodoxo de las pruebas de significación de hipótesis nula (PSHN). Comprender cómo funciona PSHN es una necesidad absoluta porque ha sido el enfoque dominante de la estadística inferencial desde que cobró importancia a principios del siglo XX. Es en lo que la gran mayoría de los científicos en activo confían para sus análisis de datos, por lo que incluso si lo odias, debes conocerlo. Sin embargo, el enfoque no está exento de problemas. Hay una serie de peculiaridades en el marco, rarezas históricas sobre cómo llegó a ser, disputas teóricas sobre si el marco es correcto o no, y muchas trampas prácticas para los incautos. No voy a entrar en muchos detalles sobre este tema, pero creo que vale la pena discutir brevemente algunas de estas cuestiones.

9.9.1 Neyman contra Fisher

Lo primero que debe tener en cuenta es que la PSHN ortodoxa es en realidad una combinación de dos enfoques bastante diferentes para las pruebas de hipótesis, uno propuesto por Sir Ronald Fisher y el otro por Jerzy Neyman (ver Lehmann (2011) para un resumen histórico). La historia es confusa porque Fisher y Neyman eran personas reales cuyas opiniones cambiaron con el tiempo, y en ningún momento ninguno de ellos ofreció “la declaración definitiva” de cómo debemos interpretar su trabajo muchas décadas después. Dicho esto, he aquí un rápido resumen de lo que considero que son estos dos enfoques.

Primero, hablemos del enfoque de Fisher. Hasta donde yo sé, Fisher suponía que solo se tenía una hipótesis (la nula) y que lo que se quería hacer era averiguar si la hipótesis nula era inconsistente con los datos. Desde su perspectiva, lo que deberías hacer es comprobar si los datos son “suficientemente improbables” según la nula. De hecho, si recuerdas nuestra discusión anterior, así es como Fisher define el valor p. Según Fisher, si la hipótesis nula proporcionara una explicación muy pobre de los datos, entonces podrías rechazarla con seguridad. Pero, como no tenemos ninguna otra hipótesis con la que compararla, no hay forma de “aceptar la alternativa” porque no tenemos necesariamente una alternativa explícita. Eso es más o menos todo.

Por el contrario, Neyman pensaba que el objetivo de las pruebas de hipótesis era servir de guía para la acción y su enfoque era algo más formal que el de Fisher. Su punto de vista era que hay varias cosas que se pueden hacer (aceptar la nula o aceptar la alternativa) y el objetivo de la prueba era decir cuál es compatible con los datos. Desde esta perspectiva, es fundamental especificar correctamente la hipótesis alternativa. Si no se sabe cuál es la hipótesis alternativa, entonces no sabe lo potente que es la prueba, ni siquiera qué acción tiene sentido. Su marco requiere realmente una competición entre diferentes hipótesis. Para Neyman, el valor $p$ no medía directamente la probabilidad de los datos (o datos más extremos) bajo la nula, era más una descripción abstracta sobre qué “posibles pruebas” te decían que aceptaras la nula, y qué “posibles pruebas” te decían que aceptaras la alternativa.

Como puedes ver, lo que tenemos hoy es una mezcla extraña de los dos. Hablamos de tener tanto una hipótesis nula como una alternativa (Neyman), pero generalmente ¹³ definimos el valor de $p$ en términos de datos extremos (Fisher), pero seguimos teniendo $\alpha$ valores (Neyman). Algunas de las pruebas estadísticas han especificado explícitamente alternativas (Neyman), pero otras son bastante vagas al respecto (Fisher). Y, según algunas personas al menos, no se nos permite hablar de aceptar la alternativa (Fisher). Es un lío, pero espero que esto al menos explique por qué es un lío.

9.9.2 Bayesianos versus frecuentistas

Anteriormente en este capítulo, fui bastante enfática sobre el hecho de que no puedes interpretar el valor p como la probabilidad de que la hipótesis nula sea verdadera. PSHN es fundamentalmente una herramienta frecuentista (consulta Chapter 7) y, como tal, no permite asignar probabilidades a las hipótesis. La hipótesis nula es cierta o no lo es. El enfoque bayesiano de la estadística interpreta la probabilidad como un grado de creencia, por lo que es totalmente correcto decir que existe una probabilidad del $10\%$ de que la hipótesis nula sea cierta. Eso es solo un reflejo del grado de confianza que tienes en esta hipótesis. Esto no está permitido dentro del enfoque frecuentista. Recuerda, si eres frecuentista, una probabilidad solo se puede definir en términos de lo que sucede después de un gran número de repeticiones independientes (es decir, una frecuencia de largo plazo). Si esta es tu interpretación de la probabilidad, hablar de la “probabilidad” de que la hipótesis nula sea cierta es un completo galimatías: una hipótesis nula o es verdadera o es falsa. Es imposible hablar de una frecuencia de largo plazo para esta afirmación. Hablar de “la probabilidad de la hipótesis nula” es tan absurdo como “el color de la libertad”. No tiene uno.

Lo más importante es que no se trata de una cuestión puramente ideológica. Si decides que eres bayesiana y que te parece bien hacer afirmaciones probabilísticas sobre hipótesis, tienes que seguir las reglas bayesianas para calcular esas probabilidades. Hablaré más sobre esto en Chapter 16, pero por ahora lo que quiero señalarte es que el valor p es una terrible aproximación a la probabilidad de que $H_0$ sea cierta. Si lo que quieres saber es la probabilidad de la nula, ¡entonces el valor p no es lo que estás buscando!

9.9.3 Trampas

Como puedes ver, la teoría que subyace a las pruebas de hipótesis es un lío, e incluso ahora hay discusiones en estadística sobre cómo “debería” funcionar. Sin embargo, los desacuerdos entre los estadísticos no son nuestra verdadera preocupación aquí. Nuestra verdadera preocupación es el análisis práctico de datos. Y aunque el enfoque “ortodoxo” de la prueba de significancia de la hipótesis nula tiene muchos inconvenientes, incluso una bayesiana impenitente como yo estaría de acuerdo en que pueden ser útiles si se usan de manera responsable. La mayoría de las veces dan respuestas sensatas y se pueden utilizar para aprender cosas interesantes. Dejando a un lado las diversas ideologías y confusiones históricas que hemos discutido, el hecho es que el mayor peligro en toda la estadística es la irreflexión. No me refiero a la estupidez, sino literalmente a la irreflexión. La prisa por interpretar un resultado sin dedicar tiempo a pensar qué dice realmente cada prueba sobre los datos y comprobar si es coherente con la interpretación que se ha hecho. Ahí es donde está la mayor trampa.

Para dar un ejemplo de esto, considera el siguiente ejemplo (ver Gelman & Stern (2006)). Supongamos que estoy realizando mi estudio sobre PES y he decidido analizar los datos por separado para los participantes masculinos y femeninos. De los participantes masculinos, $33$ de $50$ adivinaron correctamente el color de la carta. Se trata de un efecto significativo ($p = .03$). Las mujeres acertaron $29$ de cada $50$. No es un efecto significativo ($p = .32$). Al observar esto, es muy tentador que la gente empiece a preguntarse por qué existe una diferencia entre hombres y mujeres en cuanto a sus habilidades psíquicas. Sin embargo, esto es erróneo. Si lo piensas bien, en realidad no hemos realizado una prueba que compare explícitamente a los hombres con las mujeres. Todo lo que hemos hecho es comparar a los hombres con el azar (la prueba binomial fue significativa) y comparar a las mujeres con el azar (la prueba binomial no fue significativa). Si queremos argumentar que hay una diferencia real entre los hombres y las mujeres, probablemente deberíamos realizar una prueba de la hipótesis nula de que no hay diferencia. Podemos hacerlo usando una prueba de hipótesis diferente,¹⁴ pero cuando lo hacemos resulta que no tenemos pruebas de que los hombres y las mujeres sean significativamente diferentes ($p = .54$). ¿Crees que hay alguna diferencia fundamental entre los dos grupos? Por supuesto que no. Lo que sucedió aquí es que los datos de ambos grupos (hombres y mujeres) están bastante en el límite. Por pura casualidad, uno de ellos acabó en el lado mágico de la línea $p = .05$, y el otro no. Eso no implica que los hombres y las mujeres sean diferentes. Este error es tan común que siempre hay que tener cuidado con él. La diferencia entre significativo y no significativo no es prueba de una diferencia real. Si quieres decir que hay una diferencia entre dos grupos, tienes que probar esa diferencia.

El ejemplo anterior es solo eso, un ejemplo. Lo he seleccionado porque es muy común, pero lo más importante es que el análisis de datos puede ser difícil de hacer bien. Piensa qué es lo que quieres probar, por qué quieres probarlo y si las respuestas que da tu prueba podrían tener algún sentido en el mundo real.

9.10 Resumen

Las pruebas de hipótesis nulas son uno de los elementos más ubicuos de la teoría estadística. La inmensa mayoría de artículos científicos presentan los resultados de una u otra prueba de hipótesis. Como consecuencia, es casi imposible desenvolverse en el mundo de la ciencia sin tener al menos una comprensión superficial de lo que significa un valor p, lo que hace que este sea uno de los capítulos más importantes del libro. Como de costumbre, terminaré el capítulo con un resumen rápido de las ideas clave de las que hemos hablado:

Una colección de hipótesis. Hipótesis de investigación e hipótesis estadísticas. Hipótesis nula y alternativa.
Dos tipos de errores. Tipo I y Tipo II.
[Estadísticas de prueba y distribuciones muestrales].
Contraste de hipótesis para [Tomar decisiones]
El valor p de una prueba. valores p como decisiones “suaves”
[Comunicar los resultados de una prueba de hipótesis]
[Ejecución de la prueba de hipótesis en la práctica]
Tamaño del efecto, tamaño de la muestra y potencia
[Algunos temas a considerar] con respecto a la prueba de hipótesis

Más adelante en el libro, en Chapter 16, revisaré la teoría de las pruebas de hipótesis nulas desde una perspectiva bayesiana y presentaré una serie de herramientas nuevas que puedes usar si no te gusta mucho el enfoque ortodoxo. Pero, por ahora, hemos terminado con la teoría estadística abstracta y podemos empezar a hablar de herramientas específicas de análisis de datos.

La cita proviene del texto de Wittgenstein (1922), Tractatus Logico-Philosphicus.↩︎
Nota técnica. La descripción que sigue difiere sutilmente de la descripción estándar que se da en muchos textos introductorios. La teoría ortodoxa de la prueba de hipótesis nula surgió del trabajo de Sir Ronald Fisher y Jerzy Neyman a principios del siglo XX; pero Fisher y Neymar en realidad tenían puntos de vista muy diferentes sobre cómo debería funcionar. El tratamiento estándar de las pruebas de hipótesis que utilizan la mayoría de los textos es un híbrido de los dos enfoques. El tratamiento aquí es un poco más al estilo de Neyman que la visión ortodoxa, especialmente en lo que respecta al significado del valor p.↩︎
Mis disculpas a cualquiera que realmente crea en estas cosas, pero según mi lectura de la literatura sobre PES no es razonable pensar que esto sea real. Sin embargo, para ser justos, algunos de los estudios están rigurosamente diseñados, por lo que en realidad es un área interesante para pensar sobre el diseño de la investigación psicológica. Y, por supuesto, es un país libre, así que puedes dedicar tu tiempo y esfuerzo a demostrar que me equivoco si quieres, pero no creo que sea un uso muy práctico de tu intelecto.↩︎
esta analogía solo funciona si procedes de un sistema jurídico acusatorio como Reino Unido/Estados Unidos/Australia. Según tengo entendido, el sistema inquisitorial francés es bastante diferente.↩︎
un inciso sobre el lenguaje que utilizas para hablar sobre la prueba de hipótesis. En primer lugar, hay que evitar la palabra “demostrar”. Una prueba estadística realmente no demuestra que una hipótesis sea verdadera o falsa. La prueba implica certeza y, como dice el refrán, la estadística significa nunca tener que decir que estás seguro. En eso casi todo el mundo está de acuerdo. Sin embargo, más allá de eso, hay bastante confusión. Algunas personas sostienen que solo se pueden hacer afirmaciones como “rechazó la nula”, “no rechazó la nula” o posiblemente “retuvo la nula”. Según esta línea de pensamiento, no se pueden decir cosas como “acepta la alternativa” o “acepta la nula”. Personalmente creo que esto es demasiado fuerte. En mi opinión, confunde la prueba de hipótesis nulas con la visión falsacionista del proceso científico de Karl Popper. Aunque hay similitudes entre el falsacionismo y la prueba de hipótesis nula, no son equivalentes. Sin embargo, aunque personalmente creo que está bien hablar de aceptar una hipótesis (con la condición de que “aceptar” no significa que sea necesariamente cierta, especialmente en el caso de la hipótesis nula), mucha gente no estará de acuerdo. Y lo que es más, deberías ser consciente de que esta rareza particular existe para que no te pille desprevenida cuando escribas tus propios resultados.↩︎
Estrictamente hablando, la prueba que acabo de construir tiene $\alpha = .057$, que es un poco demasiado generosa. Sin embargo, si hubiera elegido 39 y 61 como límites de la región crítica, ésta solo cubriría $3.5\%$ de la distribución. Pensé que tiene más sentido usar $40$ y $60$ como mis valores críticos, y estar dispuesta a tolerar una tasa de error tipo I de $5.7\%$, ya que eso es lo más cerca que puedo llegar a un valor de $\alpha = .05$.↩︎
Internet parece bastante convencido de que Ashley dijo esto, aunque no puedo encontrar a nadie dispuesto a dar una fuente para la afirmación.↩︎
¡Eso es $p = .0000000000000000000000000136$ para las personas a las que no les gusta la notación científica!↩︎
Ten en cuenta que la p aquí no tiene nada que ver con un valor de $p$. El argumento $p$ en la prueba binomial de jamovi corresponde a la probabilidad de dar una respuesta correcta, según la hipótesis nula. En otras palabras, es el valor $\theta$.↩︎
Ten en cuenta que la p aquí no tiene nada que ver con un valor de $p$. El argumento $p$ en la prueba binomial de jamovi corresponde a la probabilidad de dar una respuesta correcta, según la hipótesis nula. En otras palabras, es el valor $\theta$.↩︎
Observa que el verdadero parámetro poblacional $\theta$ no corresponde necesariamente a un hecho inmutable de la naturaleza. En este contexto, $\theta$ no es más que la probabilidad real de que la gente adivine correctamente el color de la carta de la otra habitación. Como tal, el parámetro poblacional puede verse influido por todo tipo de cosas. Por supuesto, todo esto suponiendo que la PES exista.↩︎
Una posible excepción es cuando se estudia la efectividad de un nuevo tratamiento médico y se especifica de antemano cuál sería un tamaño de efecto importante de detectar, por ejemplo, por encima de cualquier tratamiento existente. De esta forma se puede obtener cierta información sobre el valor potencial de un nuevo tratamiento.↩︎
Aunque este libro describe la definición del valor de $p$ tanto de Neyman como de Fisher, la mayoría no lo hace. La mayoría de los libros de texto introductorios solo le darán la versión de Fisher.↩︎
En este caso, la prueba de independencia ji-cuadrado de Pearson (ver Chapter 10)↩︎

	retain \( H_0 \)	reject \( H_0 \)
\( H_0 \) is true	1-\( \alpha \) (probability of correct retention)	\(\alpha\) (type I error rate)
\( H_0 \) is false	\(\beta\) (type II error rate)	\(1 - \beta\) (power of the test)