14 ANOVA factorial
En el transcurso de los últimos capítulos hemos hecho bastante. Hemos analizado las pruebas estadísticas que puedes usar cuando tienes una variable de predicción nominal con dos grupos (por ejemplo, la prueba t en Chapter 11) o con tres o más grupos (Chapter 13). Chapter 12 introdujo una idea nueva y potente, que consiste en crear modelos estadísticos con múltiples variables predictoras continuas que se usan para explicar una única variable de resultado. Por ejemplo, se podría usar un modelo de regresión para predecir la cantidad de errores que comete un estudiante en una prueba de comprensión lectora en función de la cantidad de horas que estudió para la prueba y su puntuación en una prueba estandarizada de \(CI\).
El objetivo de este capítulo es ampliar la idea de utilizar múltiples predictores en el marco ANOVA. Por ejemplo, supongamos que estamos interesadas en usar la prueba de comprensión lectora para medir los logros del alumnado en tres escuelas diferentes, y sospechamos que las niñas y los niños se están desarrollando a ritmos diferentes (y, por lo tanto, se espera que tengan un desempeño diferente en promedio). Cada estudiante se clasifica de dos maneras diferentes: en función de su género y en función de su escuela. Lo que nos gustaría hacer es analizar las puntuaciones de comprensión lectora en términos de estas dos variables de agrupación. La herramienta para hacerlo se denomina genéricamente ANOVA factorial. Sin embargo, dado que tenemos dos variables de agrupación, a veces nos referimos al análisis como un ANOVA de dos vías, en contraste con los ANOVA de una vía que ejecutamos en Chapter 13.
14.1 ANOVA factorial 1: diseños balanceados, centrados en los efectos principales
Cuando discutimos el análisis de varianza en Chapter 13, asumimos un diseño experimental bastante simple. Cada persona está en uno de varios grupos y queremos saber si estos grupos tienen puntuaciones medias diferentes en alguna variable de resultado. En esta sección, analizaré una clase más amplia de diseños experimentales conocidos como diseños factoriales, en los que tenemos más de una variable de agrupación. Di un ejemplo de cómo podría surgir este tipo de diseño arriba. Otro ejemplo aparece en Chapter 13 en el que estábamos viendo el efecto de diferentes fármacos en el estado de ánimo.ganancia experimentado por cada persona. En ese capítulo encontramos un efecto significativo del fármaco, pero al final del capítulo también hicimos un análisis para ver si había un efecto de la terapia. No encontramos ninguno, pero hay algo un poco preocupante al tratar de ejecutar dos análisis separados para intentar predecir el mismo resultado. ¿Tal vez en realidad hay un efecto de la terapia sobre el aumento del estado de ánimo, pero no pudimos encontrarlo porque estaba “oculto” por el efecto del fármaco? En otras palabras, vamos a querer ejecutar un único análisis que incluya tanto el fármaco como la terapia como predictores. Para este análisis, cada persona se clasifica en forma cruzada según el fármaco que recibió (un factor con 3 niveles) y la terapia que recibió (un factor con 2 niveles). Nos referimos a esto como un diseño factorial de \(3 \times 2\).
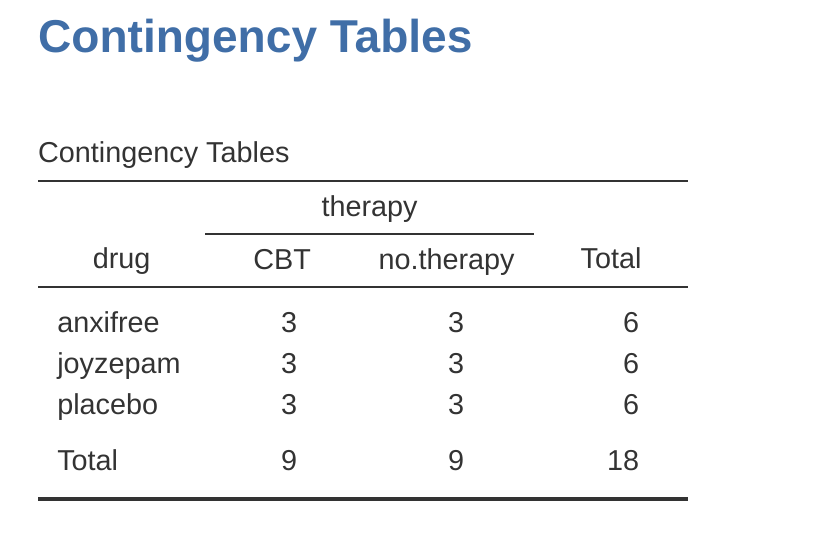
Si tabulamos de forma cruzada el fármaco por terapia, usando el análisis de ‘Frecuencias’ - ‘Tablas de contingencia’ en jamovi (ver Section 6.1), obtenemos la tabla que se muestra en Figure 14.1 .
Como puedes ver, no solo tenemos participantes correspondientes a todas las combinaciones posibles de los dos factores, lo que indica que nuestro diseño es completamente cruzado, resulta que hay un número igual de personas en cada grupo. En otras palabras, tenemos un diseño equilibrado. En esta sección explicaré cómo analizar datos de diseños equilibrados, ya que este es el caso más simple. La historia de los diseños desequilibrados es bastante tediosa, así que la dejaremos de lado por el momento.
14.1.1 ¿Qué hipótesis estamos probando?
Al igual que ANOVA unifactorial, ANOVA factorial es una herramienta para probar ciertos tipos de hipótesis sobre las medias de la población. Entonces, una buena forma de comenzar sería explicitar cuáles son realmente nuestras hipótesis. Sin embargo, antes de que podamos llegar a ese punto, es realmente útil tener una notación limpia y simple para describir las medias de la población. Dado que las observaciones se clasifican de forma cruzada en términos de dos factores diferentes, hay muchas medias diferentes en las que podríamos estar interesadas. Para ver esto, comencemos pensando en todas las diferentes medias muestrales que podemos calcular para este tipo de diseño. En primer lugar, está la idea obvia de que podríamos estar interesadas en esta lista de medias grupales (Table 14.1).
| drug | therapy | mood.gain |
|---|---|---|
| placebo | no.therapy | 0.30 |
| anxifree | no.therapy | 0.40 |
| joyzepam | no.therapy | 1.47 |
| placebo | CBT | 0.60 |
| anxifree | CBT | 1.03 |
| joyzepam | CBT | 1.50 |
Ahora, la siguiente tabla (Table 14.2) muestra una lista de las medias de los grupos para todas las combinaciones posibles de los dos factores (p. ej., personas que recibieron el placebo y ninguna terapia, personas que recibieron el placebo mientras recibían TCC, etc. .). Es útil organizar todos estos números, más las medias marginales y generales, en una sola tabla como esta:
| no therapy | CBT | total | |
|---|---|---|---|
| placebo | 0.30 | 0.60 | 0.45 |
| anxifree | 0.40 | 1.03 | 0.72 |
| joyzepam | 1.47 | 1.50 | 1.48 |
| total | 0.72 | 1.04 | 0.88 |
Ahora bien, cada una de estas diferentes medias es, por supuesto, un estadístico muestral. Es una cantidad que pertenece a las observaciones específicas que hemos hecho durante nuestro estudio. Sobre lo que queremos hacer inferencias son los parámetros de población correspondientes. Es decir, las verdaderas medias tal como existen dentro de una población más amplia. Esas medias poblacionales también se pueden organizar en una tabla similar, pero necesitaremos un poco de notación matemática para hacerlo (Table 14.3). Como de costumbre, usaré el símbolo \(\mu\) para indicar la media de una población. Sin embargo, debido a que hay muchas medias diferentes, tendré que usar subíndices para distinguirlas.
Así es como funciona la notación. Nuestra tabla se define en términos de dos factores. Cada fila corresponde a un nivel diferente del Factor A (en este caso, fármaco), y cada columna corresponde a un nivel diferente del Factor B (en este caso, terapia). Si dejamos que R indique el número de filas en la tabla y \(C\) indique el número de columnas, podemos referirnos a esto como un ANOVA factorial \(R \times C\). En este caso \(R = 3\) y \(C = 2\). Usaremos letras minúsculas para referirnos a filas y columnas específicas, por lo que \(\mu_{rc}\) se refiere a la media poblacional asociada con el nivel \(r\)-ésimo del Factor \(A\) (es decir, el número de fila \(r\)) y el \(c\)-ésimo nivel del Factor B (columna número c).1 Entonces, las medias poblacionales ahora se escriben como en Table 14.1:
| no therapy | CBT | total | |
|---|---|---|---|
| placebo | \( \mu_{11} \) | \( \mu_{12} \) | |
| anxifree | \( \mu_{21} \) | \( \mu_{22} \) | |
| joyzepam | \( \mu_{31} \) | \( \mu_{32} \) | |
| total |
Bien, ¿qué pasa con las entradas restantes? Por ejemplo, ¿cómo deberíamos describir el aumento promedio del estado de ánimo en toda la población (hipotética) de personas que podrían recibir Joyzepam en un experimento como este, independientemente de si estaban en TCC? Usamos la notación “punto” para expresar esto. En el caso de Joyzepam, fíjate que estamos hablando de la media asociada con la tercera fila de la tabla. Es decir, estamos promediando las medias de dos celdas (es decir, \(\mu_{31}\) y \(\mu_{32}\)). El resultado de este promedio se denomina media marginal y se denotaría \(\mu_3.\) en este caso. La media marginal para la TCC corresponde a la media poblacional asociada a la segunda columna de la tabla, por lo que usamos la notación porque es la media obtenida al promediar (marginalizar2) sobre ambas. Entonces, nuestra tabla completa de medias poblacionales se puede escribir como en Table 14.4.
| no therapy | CBT | total | |
|---|---|---|---|
| placebo | \( \mu_{11} \) | \( \mu_{12} \) | \( \mu_{1.} \) |
| anxifree | \( \mu_{21} \) | \( \mu_{22} \) | \( \mu_{2.} \) |
| joyzepam | \( \mu_{31} \) | \( \mu_{32} \) | \( \mu_{3.} \) |
| total | \( \mu_{.1} \) | \( \mu_{.2} \) | \( \mu_{..} \) |
Ahora que tenemos esta notación, es sencillo formular y expresar algunas hipótesis. Supongamos que el objetivo es averiguar dos cosas. Primero, ¿la elección del fármaco tiene algún efecto sobre el estado de ánimo? Y segundo, ¿la TCC tiene algún efecto sobre el estado de ánimo? Por supuesto, estas no son las únicas hipótesis que podríamos formular, y veremos un ejemplo realmente importante de un tipo diferente de hipótesis en la sección [ANOVA factorial 2: diseños balanceados, interacciones permitidas], pero estas son las dos hipótesis más simples para poner a prueba, así que empezaremos por ahí. Considera la primera prueba. Si el fármaco no tiene efecto entonces esperaríamos que todas las medias de la fila fueran idénticas, ¿verdad? Así que esa es nuestra hipótesis nula. Por otro lado, si el fármaco sí importa, deberíamos esperar que estas medias de fila sean diferentes. Formalmente, escribimos nuestras hipótesis nula y alternativa en términos de igualdad de medias marginales:
\[\text{Hipótesis nula, } H_0 \text{: las medias de las filas son las mismas, es decir, } \mu_{1. } = \mu_{2. } = \mu_{3. }\]
\[\text{Hipótesis alternativa, } H_1 \text{: la media de al menos una fila es diferente}\]
Vale la pena señalar que estas son exactamente las mismas hipótesis estadísticas que formamos cuando ejecutamos un ANOVA unifactorial en estos datos en Chapter 13. En aquel entonces, usé la notación \(\mu \times {P}\) para referirme a la ganancia media en el estado de ánimo del grupo placebo, con \(\mu{A}\) y \(\mu \times {J}\) correspondientes a las medias del grupo. para los dos fármacos, y la hipótesis nula fue \(\mu{P} = \mu{A} = \mu{J}\) . Entonces, en realidad estamos hablando de la misma hipótesis, solo que el ANOVA más complicado requiere una notación más cuidadosa debido a la presencia de múltiples variables de agrupación, por lo que ahora nos referimos a esta hipótesis como \(\mu_{ 1.} = \mu_{ 2.} = \mu_{ 3.}\) . Sin embargo, como veremos en breve, aunque la hipótesis es idéntica, la prueba de esa hipótesis es sutilmente diferente debido al hecho de que ahora estamos reconociendo la existencia de la segunda variable de agrupación.
Hablando de la otra variable de agrupación, no te sorprenderás al descubrir que nuestra segunda prueba de hipótesis está formulada de la misma manera. Sin embargo, dado que estamos hablando de terapia psicológica en lugar de fármacos, nuestra hipótesis nula ahora corresponde a la igualdad de las medias de la columna:
\[\text{Hipótesis nula, } H_0 \text{: las medias de las columnas son las mismas, es decir, } \mu_{ .1} = \mu_{ .2} \] \[\text{Hipótesis alternativa, } H_1 \text{: las medias de las columnas son diferentes, es decir, } \mu_{ .1} \neq \mu_{ .2}\]
14.1.2 Ejecutando el análisis en jamovi
Las hipótesis nula y alternativa que describí en la última sección deberían parecer terriblemente familiares. Son básicamente las mismas que las hipótesis que estábamos probando en nuestros ANOVA unifactoriales más simples en Chapter 13. Por lo tanto, probablemente estés esperando que las pruebas de hipótesis que se utilizan en ANOVA factorial sean esencialmente las mismas que la prueba F de Chapter 13. Esperas ver referencias a sumas de cuadrados (SC), medias cuadráticas (MC), grados de libertad (gl) y, finalmente, un estadístico F que podemos convertir en un valor p, ¿verdad? Bueno, tienes toda la razón. Tanto es así que voy a apartarme de mi enfoque habitual. A lo largo de este libro, generalmente he tomado el enfoque de describir la lógica (y hasta cierto punto las matemáticas) que sustentan un análisis particular primero y solo luego introducir el análisis en jamovi. Esta vez lo haré al revés y te mostraré cómo hacerlo primero en jamovi. La razón para hacer esto es que quiero resaltar las similitudes entre la herramienta ANOVA unifactorial simple que discutimos en Chapter 13, y el enfoque más complicado que vamos a usar en este capítulo.
Si los datos que estás tratando de analizar corresponden a un diseño factorial balanceado, entonces ejecutar tu análisis de varianza es fácil. Para ver lo fácil que es, comencemos reproduciendo el análisis original de Chapter 13. En caso de que lo hayas olvidado, para ese análisis usamos un solo factor (es decir, fármaco) para predecir nuestra variable de resultado (es decir, estado de ánimo.ganancia), y obtuvimos los resultados que se muestran en Figure 14.2.
Ahora, supongamos que también tengo curiosidad por saber si la terapia tiene una relación con el aumento del estado de ánimo. A la luz de lo que hemos visto de nuestra discusión sobre la regresión múltiple en Chapter 12, probablemente no te sorprenda que todo lo que tenemos que hacer es agregar la terapia como un segundo ‘Factor fijo’ en el análisis, ver Figure 14.3.

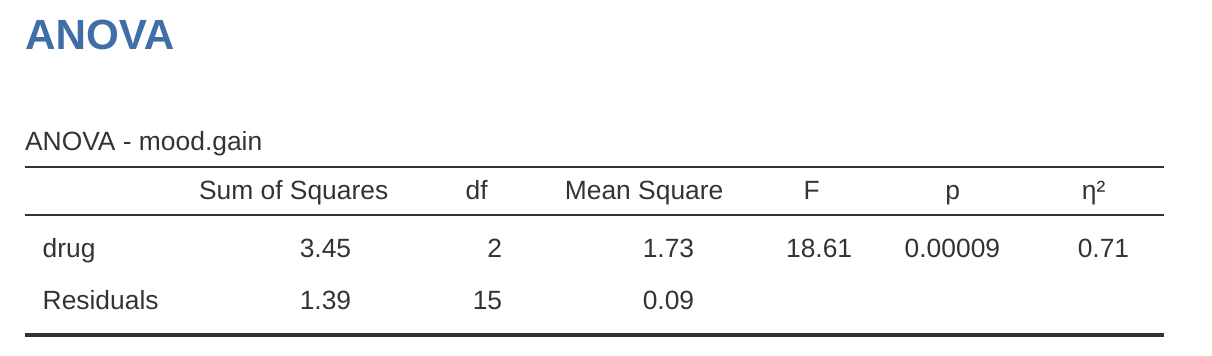
Esta salida es bastante simple de leer también. La primera fila de la tabla informa un valor de suma de cuadrados (SC) entre grupos asociado con el factor de fármaco, junto con un valor de gl entre grupos correspondiente. También calcula un valor de la media cuadrática (MC), un estadístico F y un valor p. También hay una fila que corresponde al factor de terapia y una fila que corresponde a los residuales (es decir, la variación dentro de los grupos).
No solo todas las cantidades individuales son bastante familiares, sino que las relaciones entre estas diferentes cantidades se han mantenido sin cambios, tal como vimos con el ANOVA unifactorial original. Ten en cuenta que el valor de la media cuadrática se calcula dividiendo \(SS\) por el \(df\) correspondiente. Es decir, sigue siendo cierto que
\[MS=\frac{SS}{df}\]
independientemente de si estamos hablando de fármacos, terapia o los residuales. Para ver esto, no nos preocupemos por cómo se calculan los valores de las sumas de cuadrados. En su lugar, confiemos en que jamovi ha calculado correctamente los valores de \(SS\) e intentemos verificar que el resto de los números tengan sentido. Primero, ten en cuenta que para el factor de fármacos, dividimos \(3.45\) por \(2\) y terminamos con un valor de la media cuadrática de \(1.73\). Para el factor de terapia, solo hay 1 grado de libertad, por lo que nuestros cálculos son aún más simples: dividir \(0.47\) (el valor de \(SS\)) entre 1 nos da una respuesta de \(0.47\) (el valor de \(MS\)).
Volviendo a los estadísticos F y los valores p, fíjate que tenemos dos de cada uno; uno correspondiente al factor fármaco y otro correspondiente al factor terapia. Independientemente de cuál estemos hablando, el estadístico F se calcula dividiendo el valor de la media cuadrática asociado con el factor por el valor de la media cuadrática asociado con los residulaes. Si usamos “A” como notación abreviada para referirnos al primer factor (factor A; en este caso fármaco) y “R” como notación abreviada para referirnos a los residuales, entonces el estadístico F asociado con el factor A se denota como FA, y se calcula de la siguiente manera:
\[F_A=\frac{MS_A}{MS_R}\]
y existe una fórmula equivalente para el factor B (es decir, terapia). Ten en cuenta que este uso de “R” para referirse a los residuales es un poco incómodo, ya que también usamos la letra R para referirnos al número de filas en la tabla, pero solo voy a usar “R” para referirme a los residuales en el contexto de SCR y MCR, así que espero que esto no sea confuso. De todos modos, para aplicar esta fórmula al factor fármacos cogemos la media cuadrática de 1,73 y lo dividimos por el valor de la media cuadrática residual de \(0,07\), lo que nos da un estadístico F de 26,15. El cálculo correspondiente para la variable de terapia sería dividir \(0.47\) por \(0.07\) lo que da \(7.08\) como estadístico F. Por supuesto, no sorprende que estos sean los mismos valores que jamovi ha informado en la tabla ANOVA anterior.
También en la tabla ANOVA está el cálculo de los valores de p. Una vez más, no hay nada nuevo aquí. Para cada uno de nuestros dos factores, lo que intentamos hacer es probar la hipótesis nula de que no existe una relación entre el factor y la variable de resultado (seré un poco más precisa sobre esto más adelante). Con ese fin, (aparentemente) hemos seguido una estrategia similar a la que hicimos en el ANOVA unifactorial y hemos calculado un estadístico F para cada una de estas hipótesis. Para convertirlos en valores p, todo lo que debemos hacer es observar que la distribución muestral para el estadístico F bajo la hipótesis nula (el factor en cuestión es irrelevante) es una distribución F. También ten en cuenta que los valores de los dos grados de libertad son los correspondientes al factor y los correspondientes a los residuales. Para el factor de fármacos, estamos hablando de una distribución F con 2 y 14 grados de libertad (hablaré de los grados de libertad con más detalle más adelante). En cambio, para el factor de terapia la distribución muestral es F con 1 y 14 grados de libertad.
En este punto, espero que puedas ver que la tabla ANOVA para este análisis factorial más complicado debe leerse de la misma manera que la tabla ANOVA para el análisis unifactorial más simple. En resumen, nos dice que el ANOVA factorial para nuestro diseño de \(3 x 2\) encontró un efecto significativo del fármaco (\(F_{2,14} = 26,15, p < 0,001\)), así como un efecto significativo de la terapia ( \(F_{1,14} = 7.08, p = .02\)). O, para usar la terminología más técnicamente correcta, diríamos que hay dos efectos principales del fármaco y la terapia. Por el momento, probablemente parezca un poco redundante referirse a estos como efectos “principales”, pero en realidad tiene sentido. Más adelante, vamos a querer hablar sobre la posibilidad de “interacciones” entre los dos factores, por lo que generalmente hacemos una distinción entre efectos principales y efectos de interacción.
14.1.3 ¿Cómo se calcula la suma de cuadrados?
En el apartado anterior tenía dos objetivos. En primer lugar, mostrarte que el método jamovi necesario para hacer ANOVA factorial es prácticamente el mismo que usamos para un ANOVA unifactorial. La única diferencia es la adición de un segundo factor. En segundo lugar, quería mostrarte cómo es la tabla ANOVA en este caso, para que puedas ver desde el principio que la lógica y la estructura básicas que subyacen al ANOVA factorial son las mismas que sustentan el ANOVA unifactorial. Trata de recordarlo. Es cierto, dado que el ANOVA factorial se construye más o menos de la misma manera que el ANOVA unifactorial más simple. Pero esta sensación de familiaridad comienza a evaporarse una vez que comienzas a profundizar en los detalles. Tradicionalmente, esta sensación de consuelo es reemplazada por un impulso de insultar a los autores de libros de texto de estadística.
Bien, comencemos revisando algunos de esos detalles. La explicación que di en la última sección ilustra el hecho de que las pruebas de hipótesis para los efectos principales (del fármaco y la terapia en este caso) son pruebas F, pero lo que no hace es mostrar cómo se calculan los valores de la suma de cuadrados (SC). Tampoco te dice explícitamente cómo calcular los grados de libertad (valores gl), aunque eso es algo simple en comparación. Supongamos por ahora que solo tenemos dos variables predictoras, Factor A y Factor B. Si usamos Y para referirnos a la variable de resultado, entonces usaríamos Yrci para referirnos al resultado asociado con el i-ésimo miembro del grupo rc (es decir, nivel/fila r para el Factor A y nivel/columna c para el Factor B). Por lo tanto, si usamos \(\bar{Y}\) para referirnos a la media de una muestra, podemos usar la misma notación que antes para referirnos a las medias de grupo, medias marginales y medias generales. Es decir, \(\bar{Y}_{rc}\) es la media muestral asociada al r-ésimo nivel del Factor A y al c-ésimo nivel del Factor: \(\bar{Y}_{r.}\) sería la media marginal para el r-ésimo nivel del Factor A, \(\bar{Y}_{.c}\) sería la media marginal para el c-ésimo nivel del Factor B, y \(\bar{Y}_{..}\) es la media general. En otras palabras, nuestras medias muestrales se pueden organizar en la misma tabla que las medias poblacionales. Para los datos de nuestro ensayo clínico, esa tabla se muestra en Table 14.5.
| no therapy | CBT | total | |
|---|---|---|---|
| placebo | \( \bar{Y}_{11} \) | \( \bar{Y}_{12} \) | \( \bar{Y}_{1.} \) |
| anxifree | \( \bar{Y}_{21} \) | \( \bar{Y}_{22} \) | \( \bar{Y}_{2.} \) |
| joyzepam | \( \bar{Y}_{31} \) | \( \bar{Y}_{32} \) | \( \bar{Y}_{3.} \) |
| total | \( \bar{Y}_{.1} \) | \( \bar{Y}_{.2} \) | \( \bar{Y}_{..} \) |
Y si observamos las medios muestrales que presenté anteriormente, tenemos \(\bar{Y}_{11} = 0,30\), \(\bar{Y}_{12} = 0,60\), etc. En nuestro ejemplo del ensayo clínico, el factor de fármacos tiene 3 niveles y el factor de terapia tiene 2 niveles, entonces lo que estamos tratando de ejecutar es un ANOVA factorial de \(3 \times 2\). Sin embargo, seremos un poco más generales y diremos que el Factor A (el factor de fila) tiene niveles R y el Factor B (el factor de columna) tiene C niveles, por tanto lo que estamos ejecutando aquí es $R C $ ANOVA factorial.
[Detalle técnico adicional 3]
14.1.4 ¿Cuáles son nuestros grados de libertad?
Los grados de libertad se calculan de la misma manera que en el ANOVA unifactorial. Para cualquier factor dado, los grados de libertad son iguales al número de niveles menos 1 (es decir, \(R - 1\) para la variable de fila Factor A y \(C - 1\) para la variable de columna Factor B). Entonces, para el factor fármaco obtenemos \(df = 2\), y para el factor de terapia obtenemos \(df = 1\). Más adelante, cuando discutamos la interpretación de ANOVA como un modelo de regresión (ver Section 14.6), aclararé cómo llegamos a este número. Pero por el momento podemos usar la definición simple de grados de libertad, a saber, que los grados de libertad son iguales al número de cantidades que se observan, menos el número de restricciones. Entonces, para el factor fármaco, observamos 3 medias grupales separadas, pero están restringidas por 1 media general y, por lo tanto, los grados de libertad son 2. Para los residuales, la lógica es similar, pero no exactamente igual. El número total de observaciones en nuestro experimento es 18. Las restricciones corresponden a 1 media general, los 2 grupos adicionales significan que introduce el factor fármaco y 1 grupo adicional significa que introduce el factor terapia, por lo que nuestros grados de libertad son 14. Como fórmula, esto es \(N - 1 - (R - 1) - (C - 1)\), que se simplifica a \(N - R - C + 1\).
14.1.5 ANOVA factorial versus ANOVAs unifactoriales
Ahora que hemos visto cómo funciona un ANOVA factorial, vale la pena dedicar un momento para compararlo con los resultados de los análisis unifactoriales, porque esto nos mostrará por qué es una buena idea ejecutar el ANOVA factorial. En Chapter 13, ejecuté un ANOVA unifactorial para ver si había alguna diferencia entre los medicamentos y un segundo ANOVA unifactorial para ver si había alguna diferencia entre las terapias. Como vimos en la sección Section 14.1.1, las hipótesis nula y alternativa probadas por los ANOVA de una vía son de hecho idénticas a las hipótesis probadas por el ANOVA factorial. Mirando aún más detenidamente las tablas ANOVA, podemos ver que la suma de cuadrados asociada con los factores es idéntica en los dos análisis diferentes (3,45 para el fármaco y 0,92 para la terapia), al igual que los grados de libertad (2 para el fármaco, 1 para la terapia). ¡Pero no dan las mismas respuestas! En particular, cuando ejecutamos el ANOVA unifactorial para la terapia en Section 13.9 no encontramos un efecto significativo (el valor p fue .21). Sin embargo, cuando observamos el efecto principal de la terapia dentro del contexto del ANOVA de dos vías, obtenemos un efecto significativo (p = 0,019). Los dos análisis claramente no son lo mismo.
¿Por qué sucede eso? La respuesta está en comprender cómo se calculan los residuales. Recuerda que la idea que subyace a una prueba F es comparar la variabilidad que se puede atribuir a un factor en particular con la variabilidad que no se puede explicar (los residuales). Si ejecutas un ANOVA unifactorial para la terapia y, por lo tanto, ignoras el efecto del fármaco, ¡el ANOVA terminará volcando toda la variabilidad inducida por el fármaco en los residuales! Esto tiene el efecto de hacer que los datos parezcan más ruidosos de lo que realmente son, y el efecto de la terapia que se encontró correctamente significativo en el ANOVA de dos vías ahora se vuelve no significativo. Si ignoramos algo realmente importante (p. ej., un fármaco) cuando tratamos de evaluar la contribución de otra cosa (p. ej., una terapia), nuestro análisis se verá distorsionado. Por supuesto, está perfectamente bien ignorar las variables que son genuinamente irrelevantes para el fenómeno de interés. Si hubiéramos registrado el color de las paredes, y resultó ser un factor no significativo en un ANOVA de tres vías, estaría perfectamente bien ignorarlo e informar el ANOVA de dos vías más simple que no incluye este factor irrelevante. ¡Lo que no debes hacer es descartar variables que realmente marcan la diferencia!
14.1.6 ¿Qué tipo de resultados capta este análisis?
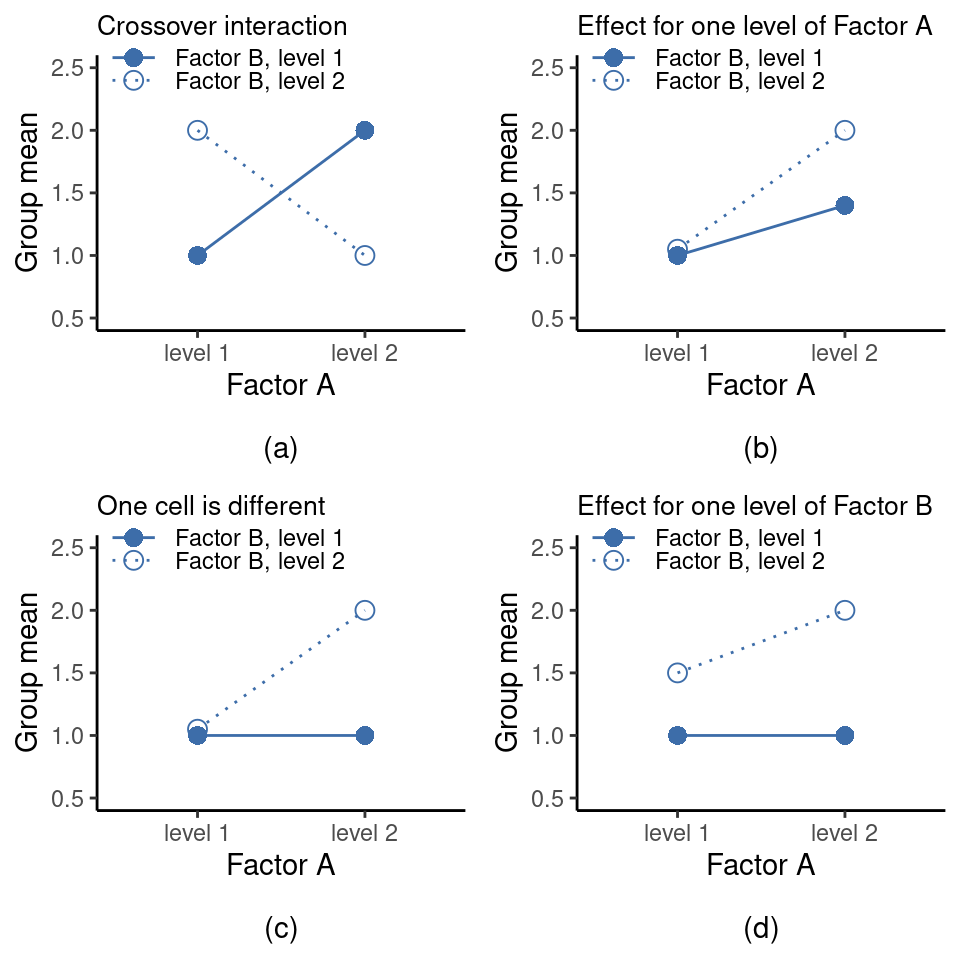
El modelo ANOVA del que hemos estado hablando hasta ahora cubre una variedad de patrones diferentes que podemos observar en nuestros datos. Por ejemplo, en un diseño ANOVA de dos vías hay cuatro posibilidades: (a) solo importa el factor A, (b) solo importa el factor B, (c) importan tanto A como B, y (d) ni A ni B importan. Un ejemplo de cada una de estas cuatro posibilidades se representa en Figure 14.4.
14.2 ANOVA factorial 2: diseños balanceados, interpretación de las interacciones
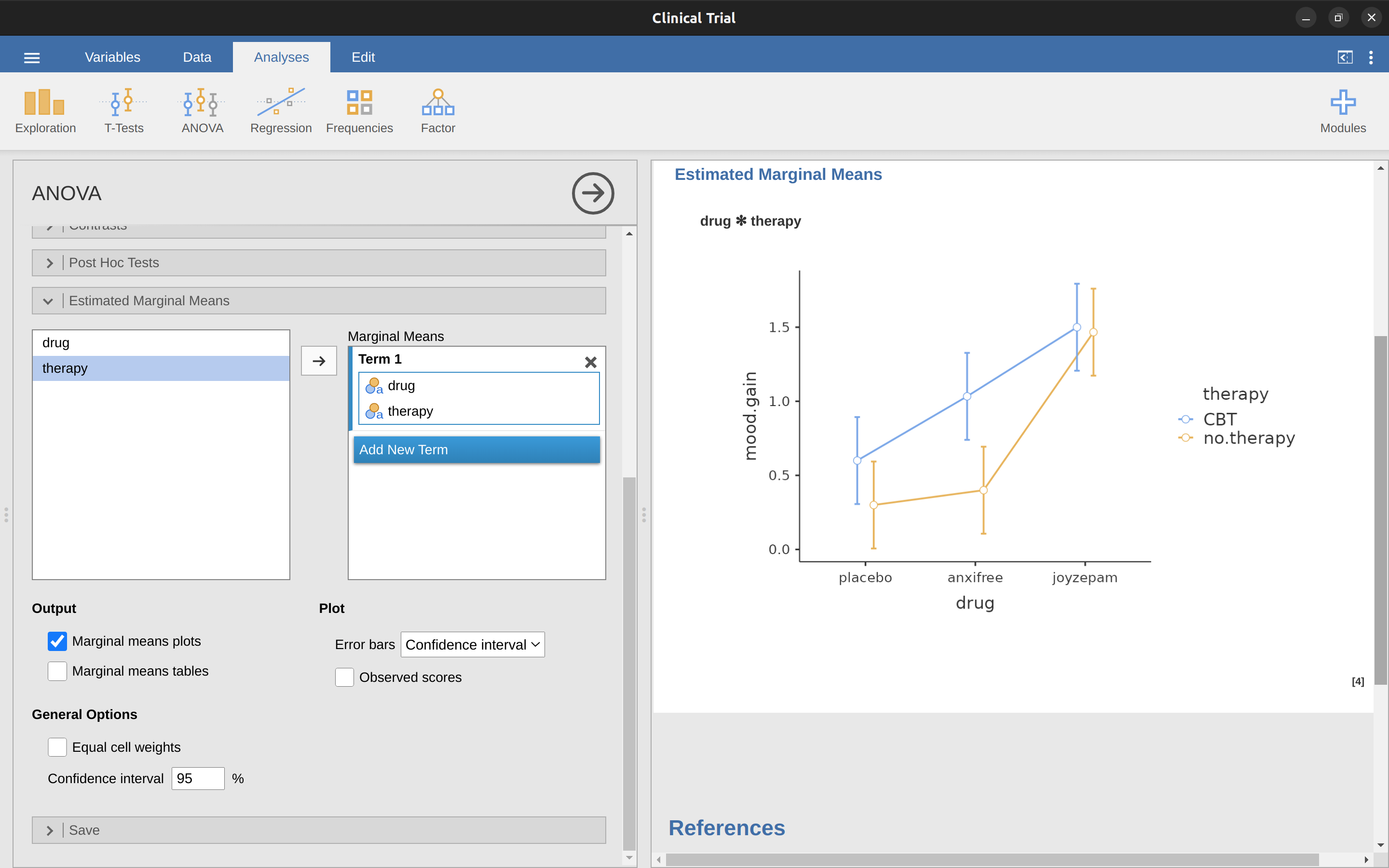
Los cuatro patrones de datos que se muestran en Figure 14.4 son bastante realistas. Hay una gran cantidad de conjuntos de datos que producen exactamente esos patrones. Sin embargo, no son todos los posibles y el modelo ANOVA del que hemos estado comentando hasta este momento no es suficiente para explicar completamente una tabla de medias de grupo. ¿Por que no? Bueno, hasta ahora tenemos la capacidad de hablar sobre la idea de que los fármacos pueden influir en el estado de ánimo y la terapia puede influir en el estado de ánimo, pero no hay forma de saber si hay una interacción entre los dos. Se dice que ocurre una interacción entre \(A\) y \(B\) si el efecto del Factor \(A\) es diferente, según el nivel del Factor \(B\) del que estemos hablando. En Figure 14.5 se muestran varios ejemplos de un efecto de interacción en el contexto de un ANOVA de \(2 \times 2\). Para dar un ejemplo más concreto, supongamos que el funcionamiento de Anxifree y Joyzepam se rige por mecanismos fisiológicos bastante diferentes. Una consecuencia de esto es que mientras que Joyzepam tiene más o menos el mismo efecto sobre el estado de ánimo independientemente de si uno está en terapia, Anxifree es en realidad mucho más eficaz cuando se administra junto con la TCC. El ANOVA que desarrollamos en la sección anterior no recoge esta idea. Para tener una idea de si realmente está ocurriendo una interacción aquí, es útil trazar las distintas medias de los grupos. En jamovi, esto se hace a través de la opción ANOVA ‘Medias marginales estimadas’: simplemente mueve el fármaco y la terapia al cuadro ‘Medias marginales’ debajo del ‘Término 1’. Esto debería parecerse a Figure 14.6. Nuestra principal preocupación se relaciona con el hecho de que las dos líneas no son paralelas. El efecto de la TCC (diferencia entre la línea continua y la línea punteada) cuando el fármaco es Joyzepam (lado derecho) parece ser cercano a cero, incluso menor que el efecto de la TCC cuando se usa un placebo (lado izquierdo). Sin embargo, cuando se administra Anxifree, el efecto de la TCC es mayor que el del placebo (centro). ¿Este efecto es real o es solo una variación aleatoria debida al azar? ¡Nuestro ANOVA original no puede responder a esta pregunta, porque no tenemos en cuenta la idea de que las interacciones existen! En esta sección, solucionaremos este problema.

14.2.1 ¿Qué es exactamente un efecto de interacción?
La idea clave que vamos a presentar en esta sección es la de un efecto de interacción. En el modelo ANOVA que hemos visto hasta ahora, solo hay dos factores involucrados en nuestro modelo (es decir, el fármaco y la terapia). Pero cuando añadimos una interacción, añadimos un nuevo componente al modelo: la combinación de fármaco y terapia. Intuitivamente, la idea que subyace a un efecto de interacción es bastante sencilla. Simplemente significa que el efecto del Factor A es diferente, según el nivel del Factor B del que estemos hablando. Pero, ¿qué significa eso realmente en términos de nuestros datos? La trama en Figure 14.5 muestra varios patrones diferentes que, aunque son bastante diferentes entre sí, contarían como un efecto de interacción. Por lo tanto, no es del todo sencillo traducir esta idea cualitativa en algo matemático con lo que un estadístico pueda trabajar.
[Detalle técnico adicional 4]
14.2.2 Grados de libertad para la interacción
Calcular los grados de libertad de la interacción es, una vez más, un poco más complicado que el cálculo correspondiente de los efectos principales. Para empezar, pensemos en el modelo ANOVA como un todo. Una vez que incluimos los efectos de interacción en el modelo, permitimos que cada grupo tenga una media única, \(mu_{rc}\). Para un ANOVA factorial de \(R \times C\), esto significa que hay cantidades \(R \times C\) de interés en el modelo y solo una restricción: todas las medias de grupo deben promediar la media general. Entonces, el modelo como un todo necesita tener (\(R \times C\)) - 1 grado de libertad. Pero el efecto principal del Factor A tiene \(R - 1\) grados de libertad, y el efecto principal del Factor B tiene \(C - 1\) grados de libertad. Esto significa que los grados de libertad asociados con la interacción son
\[ \begin{aligned} df_{A:B} & = (R \times C - 1) - (R - 1) - (C - 1) \\ & = RC - R - C + 1 \\ & = (R-1)(C-1) \end{aligned} \]
que es simplemente el producto de los grados de libertad asociados con el factor de fila y el factor de columna.
¿Qué pasa con los grados de libertad residuales? Debido a que hemos agregado términos de interacción que absorben algunos grados de libertad, quedan menos grados de libertad residuales. Específicamente, ten en cuenta que si el modelo con interacción tiene un total de \((R \times C) - 1\), y hay \(N\) observaciones en su conjunto de datos que están restringidas para satisfacer 1 media general, tus grados de libertad residuales ahora se convierten en \(N - (R \times C) - 1 + 1\), o simplemente \(N - (R \times C)\).
14.2.3 Ejecución del ANOVA en jamovi
Agregar términos de interacción al modelo ANOVA en jamovi es sencillo. De hecho, es más que sencillo porque es la opción predeterminada para ANOVA. Esto significa que cuando especificas un ANOVA con dos factores, por ejemplo, fármaco y terapia, el componente de interacción (fármaco \(\times\) terapia) se agrega automáticamente al modelo 5. Cuando ejecutamos el ANOVA con el término de interacción incluido, obtenemos los resultados que se muestran en Figure 14.7.

Resulta que, aunque tenemos un efecto principal significativo del fármaco (\(F_{2,12} = 31,7, p < 0,001\)) y el tipo de terapia ($F_{1,12} = 8,6, p = 0,013 \(), no hay una interacción significativa entre los dos (\)F_{2,12} = 2,5, p = 0,125$).
14.2.4 Interpretación de los resultados
Hay un par de cosas muy importantes a considerar al interpretar los resultados del ANOVA factorial. En primer lugar, está el mismo problema que tuvimos con ANOVA unifactorial, que es que si obtienes un efecto principal significativo de (digamos) fármaco, no dice nada sobre qué fármacos son diferentes entre sí. Para averiguarlo, debes realizar análisis adicionales. Hablaremos de algunos análisis que puedes ejecutar en secciones posteriores: Diferentes formas de especificar contrastes y Pruebas post hoc. Lo mismo sucede con los efectos de interacción. Saber que hay una interacción significativa no dice nada sobre qué tipo de interacción existe. Una vez más, deberás ejecutar análisis adicionales.
En segundo lugar, existe un problema de interpretación muy peculiar que surge cuando se obtiene un efecto de interacción significativo pero no un efecto principal correspondiente. Esto sucede a veces. Por ejemplo, en la interacción cruzada que se muestra en Figure 14.5 a, esto es exactamente lo que encontrarías. En este caso, ninguno de los efectos principales sería significativo, pero el efecto de interacción sí lo sería. Esta es una situación difícil de interpretar, y la gente a menudo se confunde un poco al respecto. El consejo general que les gusta dar a los estadísticos en esta situación es que no debes prestar mucha atención a los efectos principales cuando hay una interacción. La razón por la que dicen esto es que, aunque las pruebas de los efectos principales son perfectamente válidas desde un punto de vista matemático, cuando hay un efecto de interacción significativo, los efectos principales rara vez prueban hipótesis interesantes. Recuerda de Section 14.1.1 que la hipótesis nula para un efecto principal es que las medias marginales son iguales entre sí, y que una media marginal se forma promediando varios grupos diferentes. Pero si tienes un efecto de interacción significativo, entonces sabes que los grupos que componen la media marginal no son homogéneos, por lo que no está claro por qué te interesarían esas medias marginales.
Esto es lo que quiero decir. Una vez más, sigamos con un ejemplo clínico. Supongamos que tuviéramos un diseño de \(2 \times 2\) que comparara dos tratamientos diferentes para las fobias (p. ej., desensibilización sistemática frente a inundación) y dos fármacos diferentes para reducir la ansiedad (p. ej., Anxifree frente a Joyzepam). Ahora, supongamos que descubrimos que Anxifree no tuvo efecto cuando el tratamiento fue la desensibilización, y Joyzepam no tuvo efecto cuando el tratamiento fue la inundación. Pero ambos fueron bastante efectivos para el otro tratamiento. Esta es una interacción cruzada clásica, y lo que encontraríamos al ejecutar el ANOVA es que no hay un efecto principal del fármaco, sino una interacción significativa. Ahora bien, ¿qué significa realmente decir que no hay un efecto principal? Bueno, significa que si promediamos los dos tratamientos psicológicos diferentes, entonces el efecto promedio de Anxifree y Joyzepam es el mismo. Pero, ¿por qué a alguien le interesaría eso? Cuando se trata a alguien por fobias, nunca se da el caso de que una persona pueda ser tratada usando un “promedio” de inundación y desensibilización. Eso no tiene mucho sentido. O te quedas con uno o con el otro. Para un tratamiento, un fármaco es eficaz y para el otro tratamiento, el otro fármaco es eficaz. La interacción es lo importante y el efecto principal es algo irrelevante.
Este tipo de cosas suceden a menudo. El efecto principal son las pruebas de las medias marginales, y cuando hay una interacción, a menudo nos damos cuenta de que no estamos muy interesados en las medias marginales porque implican promediar cosas que la interacción nos dice que no deben promediarse. Por supuesto, no siempre es el caso de que un efecto principal no tenga sentido cuando hay una interacción presente. A menudo, puedes obtener un gran efecto principal y una interacción muy pequeña, en cuyo caso aún puedes decir cosas como “el fármaco A es generalmente más efectivo que el fármaco B” (porque hubo un gran efecto del fármaco), pero necesitarías modificarlo un poco agregando que “la diferencia de efectividad fue diferente para diferentes tratamientos psicológicos”. En cualquier caso, el punto principal aquí es que cada vez que obtengas una interacción significativa, debes detenerte y pensar qué significa realmente el efecto principal en este contexto. No asumas automáticamente que el efecto principal es interesante.
14.3 Tamaño del efecto
El cálculo del tamaño del efecto para un ANOVA factorial es bastante similar a lo que se utiliza en el ANOVA unidireccional (consulta la sección Tamaño del efecto). Específicamente, podemos usar \(\eta^2\) (eta-cuadrado) como una forma simple de medir qué tan grande es el efecto general para cualquier término en particular. Como antes, \(\eta^2\) se define dividiendo la suma de cuadrados asociada con ese término por la suma de cuadrados total. Por ejemplo, para determinar el tamaño del efecto principal del Factor A, usaríamos la siguiente fórmula:
\[\eta_A^2=\frac{SS_A}{SS_T}\]
Como antes, esto se puede interpretar de la misma manera que \(R^2\) en regresión.6 Indica la proporción de varianza en la variable de resultado que se puede explicar por el efecto principal de Factor A. Por lo tanto, es un número que va de 0 (ningún efecto) a 1 (considera toda la variabilidad en el resultado). Además, la suma de todos los valores de \(\eta^2\), cogidos de todos los términos del modelo, sumará el total de \(R^2\) para el modelo ANOVA. Si, por ejemplo, el modelo ANOVA se ajusta perfectamente (es decir, ¡no hay ninguna variabilidad dentro de los grupos!), los valores de \(\eta^2\) sumarán 1. Por supuesto, eso rara vez sucede en la vida real.
Sin embargo, al hacer un ANOVA factorial, hay una segunda medida del tamaño del efecto que a la gente le gusta informar, conocida como \(\eta^2\) parcial. La idea que subyace a \(\eta^2\) parcial (que a veces se denomina \(p^{\eta^2}\) o \(\eta_p^2\)) es que, al medir el tamaño del efecto para un término en particular (digamos, el efecto principal del Factor A), deseas ignorar deliberadamente los otros efectos en el modelo (por ejemplo, el efecto principal del Factor B). Es decir, supondrías que el efecto de todos estos otros términos es cero y luego calcularías cuál habría sido el valor de \(\eta^2\). En realidad, esto es bastante fácil de calcular. Todo lo que tienes que hacer es quitar la suma de cuadrados asociada con los otros términos del denominador. En otras palabras, si deseas el \(\eta^2\) parcial para el efecto principal del Factor A, el denominador es solo la suma de los valores de SC para el Factor A y los residuales
\[\text{parcial}\eta_A^2= \frac{SS_A}{SS_A+SS_R}\]
Esto siempre te dará un número mayor que \(\eta^2\), que la cínica en mí sospecha que explica la popularidad de \(\eta^2\) parcial. Y una vez más obtienes un número entre 0 y 1, donde 0 representa ningún efecto. Sin embargo, es un poco más complicado interpretar lo que significa un gran valor de \(\eta^2\) parcial. En particular, ¡no puedes comparar los valores de \(\eta^2\) parcial entre términos! Supongamos, por ejemplo, que no hay ninguna variabilidad dentro de los grupos: si es así, \(SC_R = 0\). Lo que eso significa es que cada término tiene un valor de \(\eta^2\) parcial de 1. Pero eso no significa que todos los términos en tu modelo sean igualmente importantes, o que sean igualmente grandes. Todo lo que significa es que todos los términos en tu modelo tienen tamaños de efecto que son grandes en relación con la variación residual. No es comparable entre términos.
Para ver lo que quiero decir con esto, es útil ver un ejemplo concreto. Primero, echemos un vistazo a los tamaños del efecto para el ANOVA original (Table 14.6) sin el término de interacción, de Figure 14.3.
| eta.sq | partial.eta.sq | |
|---|---|---|
| drug | 0.71 | 0.79 |
| therapy | 0.10 | 0.34 |
Mirando primero los valores de \(\eta^2\), vemos que el fármaco representa el 71 % de la varianza (es decir, \(\eta^2 = 0,71\)) en el aumento del estado de ánimo, mientras que la terapia solo representa el 10 %. Esto deja un total de 19% de la variación sin contabilizar (es decir, los residuales constituyen el 19% de la variación en el resultado). En general, esto implica que tenemos un efecto muy grande 7 del fármaco y un efecto modesto de la terapia.
Ahora veamos los valores de \(\eta^2\) parcial, que se muestran en Figure 14.3. Debido a que el efecto de la terapia no es tan grande, controlarlo no genera mucha diferencia, por lo que el \(\eta^2\) parcial para el fármaco no aumenta mucho y obtenemos un valor de \(p ^{\eta^2} = 0,79\). Por el contrario, debido a que el efecto del fármaco fue muy grande, controlarlo provoca una gran diferencia, por lo que cuando calculamos el \(\eta^2\) parcial para la terapia, puedes ver que aumenta a $p{2 } = 0,34 $. La pregunta que tenemos que hacernos es, ¿qué significan realmente estos valores de \(\eta^2\) parcial? La forma en que generalmente interpreto el \(\eta^2\) parcial para el efecto principal del Factor A es interpretarlo como una declaración sobre un experimento hipotético en el que solo se varió el Factor A. Así, aunque en este experimento variamos tanto A como B, podemos imaginar fácilmente un experimento en el que solo se varió el Factor A, y el estadístico \(\eta^2\) parcial te dice cuánto de la varianza en la variable de resultado esperarías ver contabilizado en ese experimento. Sin embargo, debes tenerse en cuenta que esta interpretación, como muchas cosas asociadas con los efectos principales, no tiene mucho sentido cuando hay un efecto de interacción grande y significativo.
Hablando de efectos de interacción, Table 14.7 muestra lo que obtenemos cuando calculamos los tamaños del efecto para el modelo que incluye el término de interacción, como en Figure 14.7. Como puedes ver, los valores de \(\eta^2\) para los efectos principales no cambian, pero los valores de \(\eta^2\) parcial sí:
| eta.sq | partial.eta.sq | |
|---|---|---|
| drug | 0.71 | 0.84 |
| therapy | 0.10 | 0.42 |
| drug*therapy | 0.06 | 0.29 |
14.3.1 Medias estimadas de los grupos
En muchas situaciones, querrás estimar todas las medias de los grupos en función de los resultados de tu ANOVA, así como los intervalos de confianza asociados con ellos. Puedes usar la opción ‘Medias marginales estimadas’ en el análisis ANOVA de jamovi para hacer esto, como en Figure 14.8. Si el ANOVA que ejecutaste es un modelo saturado (es decir, contiene todos los efectos principales posibles y todos los efectos de interacción posibles), las estimaciones de las medias de los grupos son en realidad idénticas a las medias muestrales, aunque los intervalos de confianza utilizarán una estimación combinada de los errores estándar en lugar de utilizar uno para cada grupo.

En el resultado, vemos que la mejora media estimada del estado de ánimo para el grupo de placebo sin terapia fue de \(0,300\), con un intervalo de confianza de \(95\%\) de \(0,006\) a \(0,594\). Ten en cuenta que estos no son los mismos intervalos de confianza que obtendrías si los calcularas por separado para cada grupo, debido al hecho de que el modelo ANOVA asume la homogeneidad de la varianza y, por lo tanto, utiliza una estimación combinada de la desviación estándar.
Cuando el modelo no contiene el término de interacción, las medias estimadas del grupo serán diferentes de las medias muestrales. En lugar de informar la media muestral, jamovi calculará el valor de las medias del grupo que se esperaría sobre la base de las medias marginales (es decir, suponiendo que no hay interacción). Usando la notación que desarrollamos anteriormente, la estimación informada para \(\mu_{rc}\), la media para el nivel r en el Factor A (fila) y el nivel c en el Factor B (columna) sería $_{..} + _r + _c ps Si realmente no hay interacciones entre los dos factores, esta es en realidad una mejor estimación de la media poblacional que la media muestral sin procesar. Eliminar el término de interacción del modelo, a través de las opciones ‘Modelo’ en el análisis ANOVA de jamovi, proporciona las medias marginales para el análisis que se muestra en Figure 14.9.
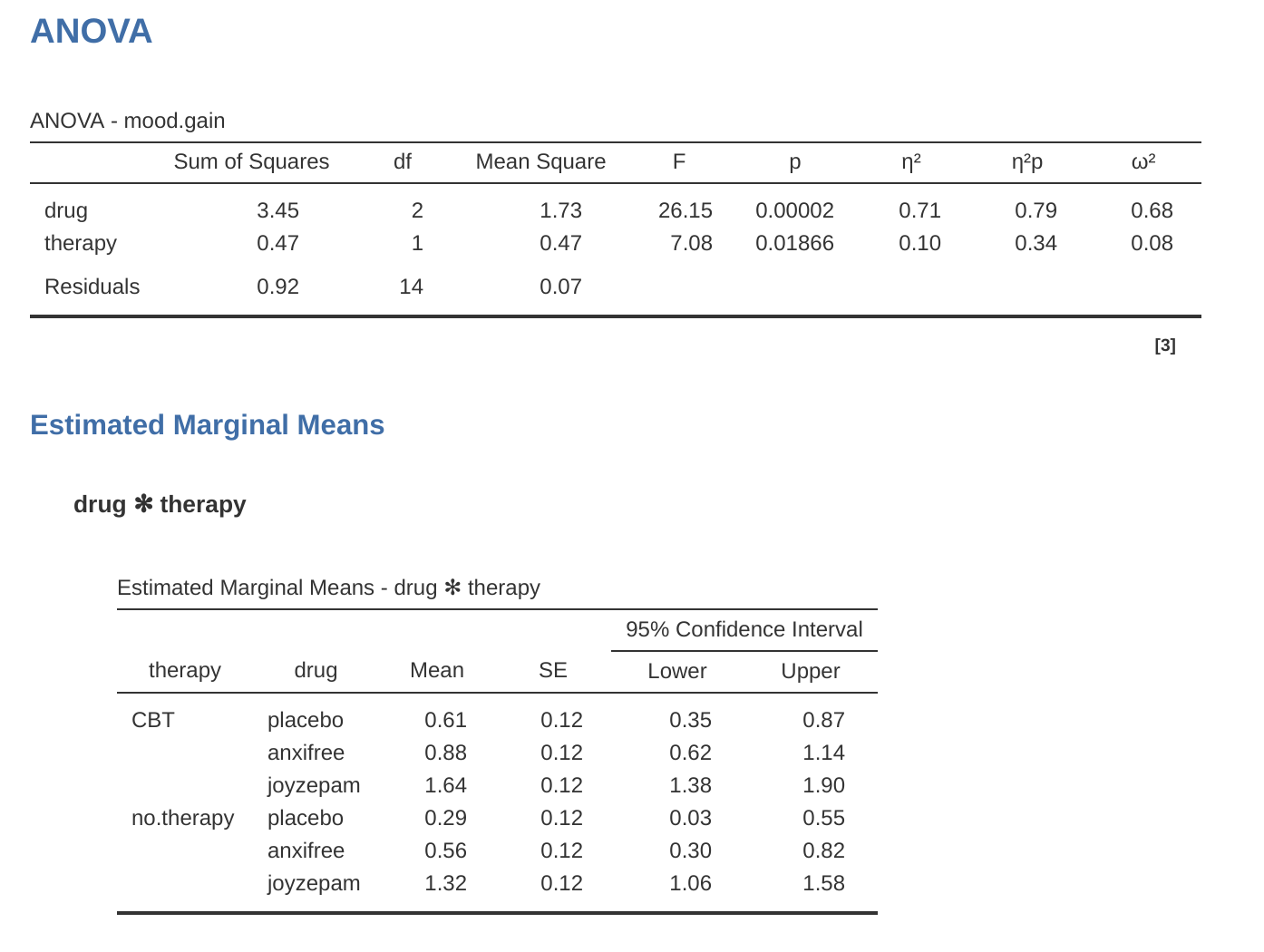
14.4 Comprobación de supuestos
Al igual que con el ANOVA unifactorial, los supuestos clave del ANOVA factorial son la homogeneidad de la varianza (todos los grupos tienen la misma desviación estándar), la normalidad de los residuales y la independencia de las observaciones. Los dos primeros son cosas que podemos verificar. El tercero es algo que debes evaluar tú misma preguntándote si existe alguna relación especial entre las diferentes observaciones, por ejemplo, medidas repetidas en las que la variable independiente es el tiempo, por lo que existe una relación entre las observaciones en el momento uno y en el momento dos: las observaciones en momentos diferentes son de las mismas personas. Además, si no estás utilizando un modelo saturado (por ejemplo, si has omitido los términos de interacción), también estás suponiendo que los términos omitidos no son importantes. Por supuesto, puedes verificar esto último ejecutando un ANOVA con los términos omitidos incluidos y ver si son significativos, por lo que es bastante fácil. ¿Qué pasa con la homogeneidad de la varianza y la normalidad de los residuales? Son bastante fáciles de verificar. No es diferente a las comprobaciones que hicimos en un ANOVA unifactorial.
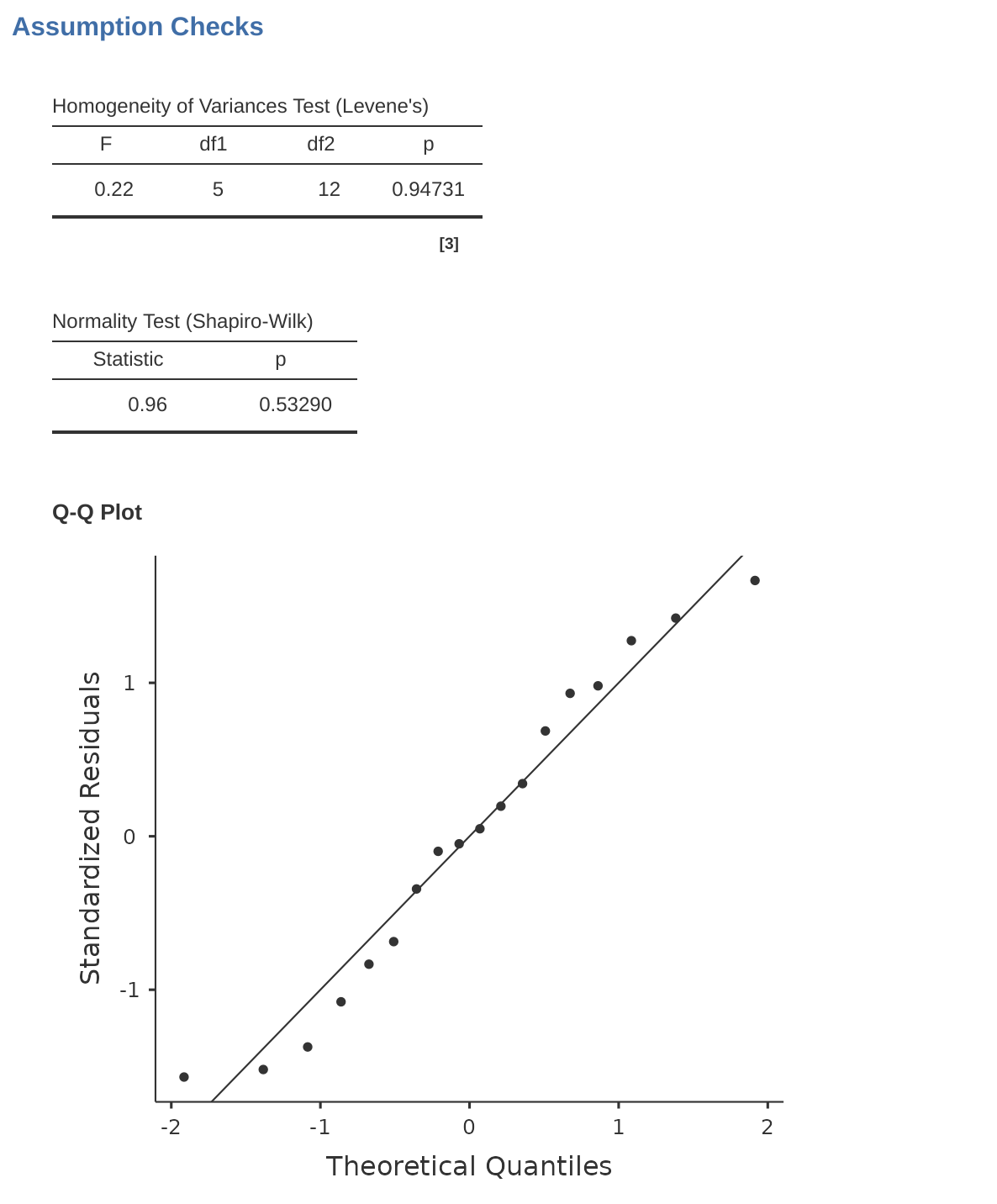
14.4.1 Homogeneidad de varianzas
Como se mencionó en Section 13.6.1 en el último capítulo, es una buena idea inspeccionar visualmente una gráfica de las desviaciones estándar comparadas entre diferentes grupos/categorías, y también ver si la prueba de Levene es consistente con la inspección visual. La teoría que subyace a la prueba de Levene se discutió en Section 13.6.1, por lo que no la discutiré nuevamente. Esta prueba espera que tengas un modelo saturado (es decir, que incluya todos los términos relevantes), porque la prueba se ocupa principalmente de la varianza dentro del grupo, y realmente no tiene mucho sentido calcular esto de otra manera que con respecto al modelo completo. La prueba de Levene se puede especificar en la opción ANOVA ‘Comprobaciones de supuestos’ - ‘Pruebas de homogeneidad’ en jamovi, con el resultado que se muestra en Figure 14.10. El hecho de que la prueba de Levene no sea significativa significa que, siempre que sea consistente con una inspección visual de la gráfica de desviaciones estándar, podemos asumir con seguridad que no se viola el supuesto de homogeneidad de varianzas.
14.4.2 Normalidad de los residuales
Al igual que con el ANOVA unifactorial, podemos probar la normalidad de los residuales de manera directa (consulta Section 13.6.4). No obstante, generalmente es una buena idea examinar los residuales gráficamente utilizando un gráfico QQ. Ver Figure 14.10.
14.5 Análisis de covarianza (ANCOVA)
Una variación en ANOVA es cuando tienes una variable continua adicional que crees que podría estar relacionada con la variable dependiente. Esta variable adicional se puede agregar al análisis como una covariable, en el acertadamente llamado análisis de covarianza (ANCOVA).
En ANCOVA, los valores de la variable dependiente se “ajustan” por la influencia de la covariable, y luego las medias de puntuación “ajustadas” se prueban entre grupos de la manera habitual. Esta técnica puede aumentar la precisión de un experimento y, por lo tanto, proporcionar una prueba más “poderosa” de la igualdad de las medias de grupo en la variable dependiente. ¿Cómo hace esto ANCOVA? Bueno, aunque la covariable en sí no suele tener ningún interés experimental, el ajuste de la covariable puede disminuir la estimación del error experimental y, por lo tanto, al reducir la varianza del error, se aumenta la precisión. Esto significa que es menos probable un fallo inapropiada para rechazar la hipótesis nula (falso negativo o error de tipo II).
A pesar de esta ventaja, ANCOVA corre el riesgo de deshacer las diferencias reales entre grupos, y esto debe evitarse. Mira Figure 14.11, por ejemplo, que muestra un gráfico de la ansiedad estadística en relación a la edad y muestra dos grupos distintos: estudiantes que tienen antecedentes o preferencias en Artes o Ciencias. ANCOVA con la edad como covariable podría llevar a la conclusión de que la ansiedad estadística no difiere en los dos grupos. ¿Sería razonable esta conclusión? Probablemente no porque las edades de los dos grupos no se superponen y el análisis de varianza esencialmente “se ha extrapolado a una región sin datos” (Everitt (1996), p. 68).
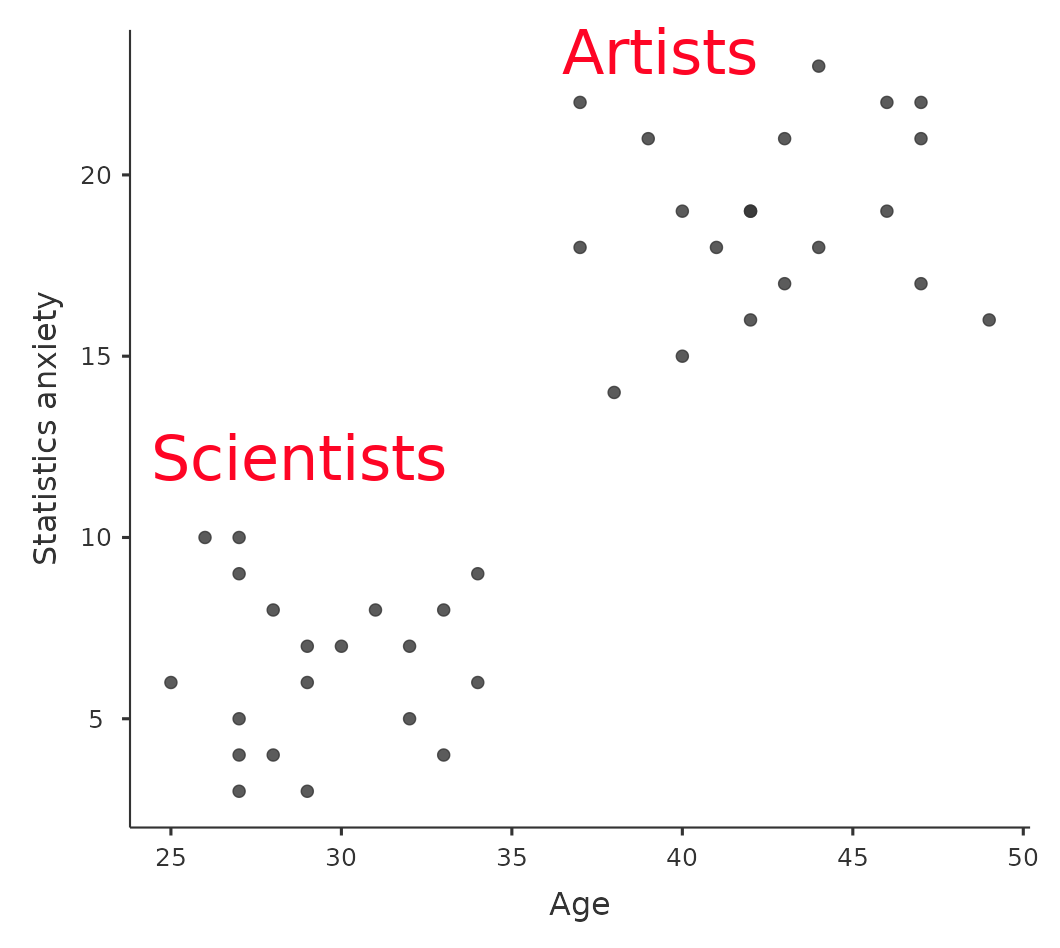
Claramente, se debe pensar detenidamente en un análisis de covarianza con grupos distintos. Esto se aplica tanto a los diseños unifactoriales como a los factoriales, ya que ANCOVA se puede utilizar con ambos.
14.5.1 Ejecución de ANCOVA en jamovi
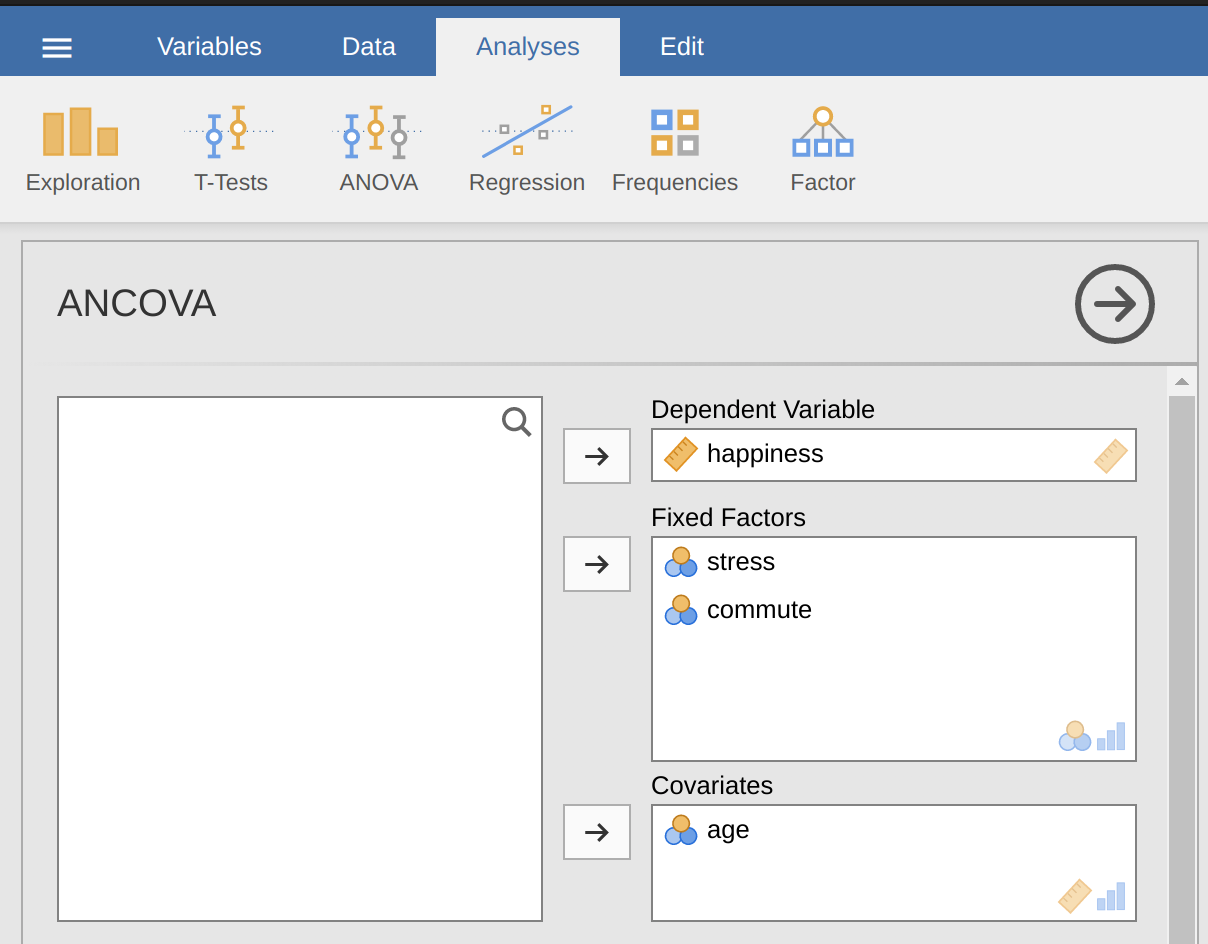
Un psicólogo de la salud estaba interesado en el efecto de la rutina de ciclismo y el estrés sobre los niveles de felicidad, con la edad como covariable. Puedes encontrar el conjunto de datos en el archivo ancova.csv. Abre este archivo en jamovi y luego, para realizar un ANCOVA, selecciona Análisis - ANOVA - ANCOVA para abrir la ventana de análisis ANCOVA (Figure 14.12). Resalta la variable dependiente ‘felicidad’ y transfiérela al cuadro de texto ‘Variable dependiente’. Resalta las variables independientes ‘estrés’ y ‘desplazamiento’ y muévelas al cuadro de texto ‘Factores fijos’. Resalta la covariable ‘edad’ y transfiérela al cuadro de texto ‘Covariables’. Luego haz clic en las medias marginales estimadas para que aparezcan las opciones de diagramas y tablas.
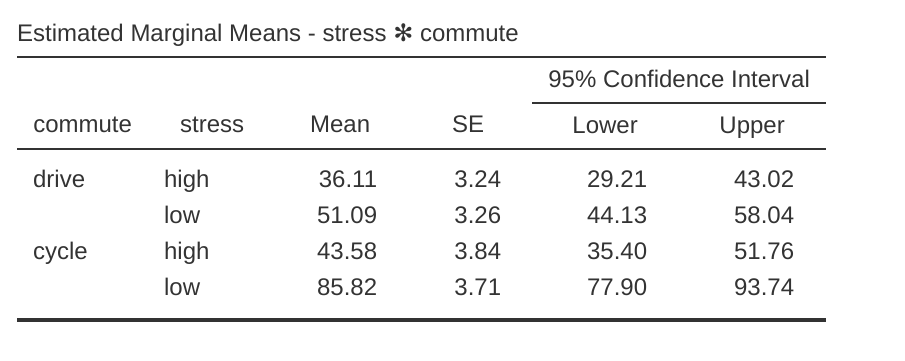
En la ventana de resultados jamovi (Figure 14.13) se genera una tabla ANCOVA que muestra las pruebas de los efectos entre sujetos. El valor de F para la covariable ‘edad’ es significativo en \(p = .023\), lo que sugiere que la edad es un predictor importante de la variable dependiente, la felicidad. Cuando observamos las puntuaciones medias marginales estimadas (Figure 14.14), se han realizado ajustes (en comparación con un análisis sin la covariable) debido a la inclusión de la covariable ‘edad’ en este ANCOVA. Un gráfico (Figure 14.15) es una buena manera de visualizar e interpretar los efectos significativos.
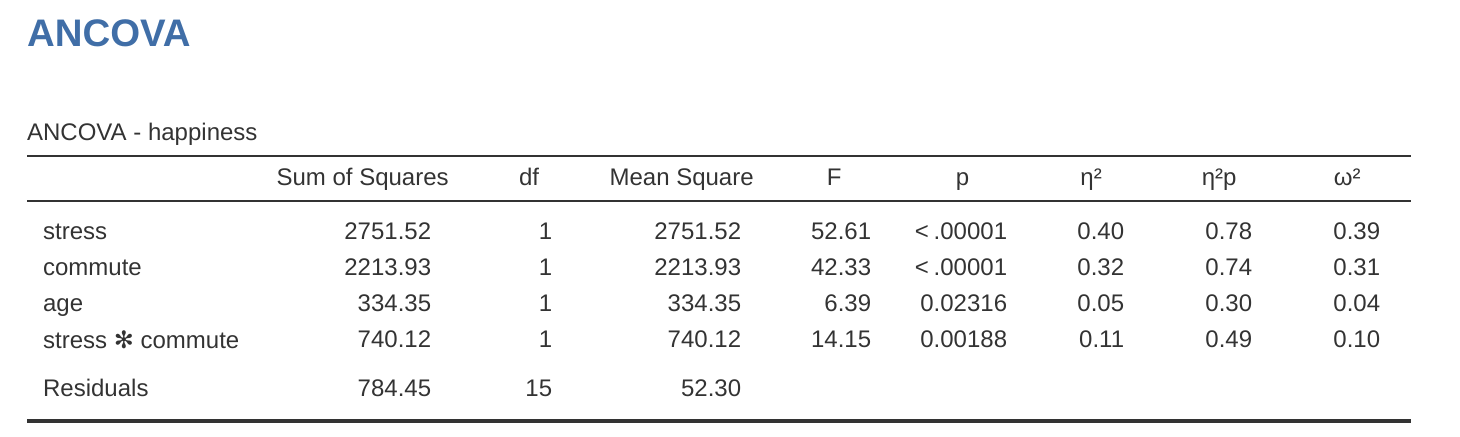
El valor \(F\) para el efecto principal ‘estrés’ (52.61) tiene una probabilidad asociada de \(p < .001\). El valor \(F\) para el efecto principal ‘desplazamiento’ (42.33) tiene una probabilidad asociada de \(p < .001\). Dado que ambos son menores que la probabilidad que normalmente se usa para decidir si un resultado estadístico es significativo (\(p < .05\)), podemos concluir que hubo un efecto principal significativo del estrés (\(F(1, 15) = 52.61, p < .001\)) y un efecto principal significativo del método de desplazamiento (\(F(1, 15) = 42.33, p < .001\)). También se encontró una interacción significativa entre el estrés y el método de desplazamiento (\(F(1, 15) = 14.15, p = .002\)).
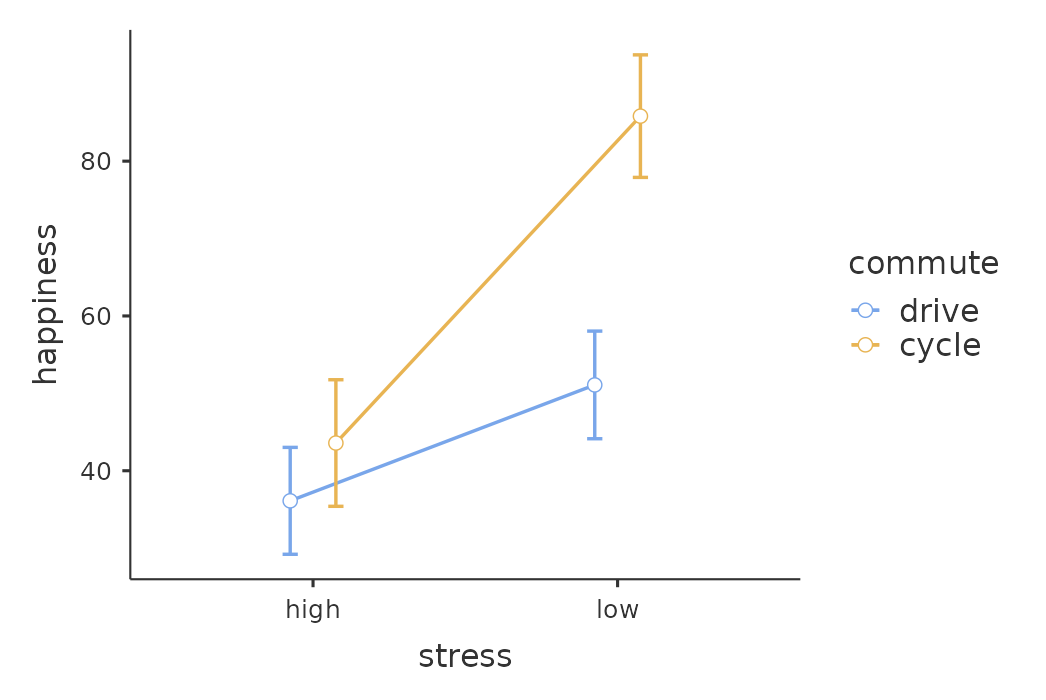
En Figure 14.15 podemos ver las puntuaciones de felicidad medias marginales ajustadas cuando la edad es una covariable en un ANCOVA. En este análisis hay un efecto de interacción significativo, por el cual las personas con poco estrés que van en bicicleta al trabajo son más felices que las personas con poco estrés que conducen y las personas con mucho estrés que van en bicicleta o en coche al trabajo. También hay un efecto principal significativo del estrés: las personas con poco estrés son más felices que las que tienen mucho estrés. Y también hay un efecto principal significativo de la conducta de de desplazamiento: las personas que van en bicicleta son más felices, en promedio, que las que conducen al trabajo.
Una cosa que debes tener en cuenta es que, si estás pensando en incluir una covariable en tu ANOVA, hay una suposición adicional: la relación entre la covariable y la variable dependiente debe ser similar para todos los niveles de la variable independiente. Esto se puede verificar agregando un término de interacción entre la covariable y cada variable independiente en la opción Modelo jamovi - Términos del modelo. Si el efecto de interacción no es significativo, se puede eliminar. Si es significativo, entonces podría ser apropiada una técnica estadística diferente y más avanzada (que está más allá del alcance de este libro, por lo que es posible que desees consultar a un estadístico amigo).
14.6 ANOVA como modelo lineal
Una de las cosas más importantes que hay que entender sobre ANOVA y regresión es que básicamente son lo mismo. A simple vista, tal vez no pensarías que esto es cierto. Después de todo, la forma en que los he descrito hasta ahora sugiere que ANOVA se ocupa principalmente de probar las diferencias de grupo, y la regresión se ocupa principalmente de comprender las correlaciones entre las variables. Y, hasta donde llega, eso es perfectamente cierto. Pero cuando miras debajo del capó, por así decirlo, la mecánica subyacente de ANOVA y la regresión son terriblemente similares. De hecho, si lo piensas bien, ya has visto evidencia de esto. Tanto ANOVA como la regresión se basan en gran medida en sumas de cuadrados (SC), ambos utilizan pruebas F, etc. Mirando hacia atrás, es difícil escapar de la sensación de que Chapter 12 y Chapter 13 eran un poco repetitivos.
La razón de esto es que ANOVA y la regresión son tipos de modelos lineales. En el caso de la regresión, esto es algo obvio. La ecuación de regresión que usamos para definir la relación entre predictores y resultados es la ecuación de una línea recta, por lo que obviamente es un modelo lineal, con la ecuación
\[Y_p=b_0+b_1 X_{1p} +b_2 X_{2p} + \epsilon_p\]
donde \(Y_p\) es el valor de resultado para la p-ésima observación (p. ej., p-ésima persona), \(X_{1p}\) es el valor del primer predictor para la p-ésima observación, \(X_{2p}\) es el valor del segundo predictor para la p-ésima observación, los términos \(b_0\), \(b_1\) y \(b_2\) son nuestros coeficientes de regresión, y \(\epsilon_p\) es el p-ésimo residuo. Si ignoramos los residuos \(\epsilon_p\) y solo nos centramos en la línea de regresión, obtenemos la siguiente fórmula:
\[\hat{Y}_p=b_0+b_1 X_{1p} +b_2 X_{2p} \]
donde \(\hat{Y}_p\) es el valor de Y que la línea de regresión predice para la persona p, a diferencia del valor realmente observado \(Y_p\). Lo que no es inmediatamente obvio es que también podemos escribir ANOVA como un modelo lineal. Sin embargo, en realidad es bastante sencillo hacerlo. Comencemos con un ejemplo realmente simple, reescribiendo un ANOVA factorial de \(2 \times 2\) como un modelo lineal.
14.6.1 Algunos datos
Para concretar las cosas, supongamos que nuestra variable de resultado es la calificación que recibe un estudiante en mi clase, una variable de escala de razón que corresponde a una nota de \(0%\) a \(100%\). Hay dos variables predictoras de interés: si el estudiante se presentó o no a las clases (la variable de asistencia) y si el estudiante realmente leyó o no el libro de texto (la variable de lectura). Diremos que atiende = 1 si el alumno asistió a clase, y atiende = 0 si no lo hizo. Del mismo modo, diremos que lectura = 1 si el estudiante leyó el libro de texto y lectura = 0 si no lo hizo.
Bien, hasta ahora eso es bastante simple. Lo siguiente que debemos hacer es ajustar algunas matemáticas alrededor de esto (¡lo siento!). Para los propósitos de este ejemplo, permite que \(Y_p\) denote la calificación del p-ésimo estudiante en la clase. Esta no es exactamente la misma notación que usamos anteriormente en este capítulo. Anteriormente, usamos la notación \(Y_{rci}\) para referirnos a la i-ésima persona en el r-ésimo grupo para el predictor 1 (el factor de fila) y el c-ésimo grupo para el predictor 2 (el factor de columna). Esta notación extendida fue realmente útil para describir cómo se calculan los valores de SC, pero es una molestia en el contexto actual, así que cambiaré la notación aquí. Ahora, la notación \(Y_p\) es visualmente más simple que \(Y_{rci}\), ¡pero tiene la desventaja de que en realidad no realiza un seguimiento de las membresías del grupo! Es decir, si te dijera que \(Y_{0,0,3} = 35\), inmediatamente sabrías que estamos hablando de un estudiante (de hecho, el tercer estudiante de este tipo) que no asistió a las clases (es decir, asistió = 0) y no leyó el libro de texto (es decir, lectura = 0), y que terminó suspendiendo la clase (nota = 35). Pero si te digo que \(Y_p = 35\), todo lo que sabes es que el p-ésimo estudiante no obtuvo una buena calificación. Aquí hemos perdido información clave. Por supuesto, no se necesita pensar mucho para descubrir cómo solucionar esto. Lo que haremos en su lugar es introducir dos nuevas variables \(X_{1p}\) y \(X_{2p}\) que realizan un seguimiento de esta información. En el caso de nuestro estudiante hipotético, sabemos que \(X_{1p} = 0\) (es decir, asistir = 0) y \(X_{2p} = 0\) (es decir, leer = 0). Entonces, los datos podrían verse como Table 14.8.
| person, \(p\) | grade, \(Y_p\) | attendance, \(X_{1p}\) | reading, \(X_{2p}\) |
|---|---|---|---|
| 1 | 90 | 1 | 1 |
| 2 | 87 | 1 | 1 |
| 3 | 75 | 0 | 1 |
| 4 | 60 | 1 | 0 |
| 5 | 35 | 0 | 0 |
| 6 | 50 | 0 | 0 |
| 7 | 65 | 1 | 0 |
| 8 | 70 | 0 | 1 |
Esto no es nada particularmente especial, por supuesto. ¡Es exactamente el formato en el que esperamos ver nuestros datos! Consulta el archivo de datos rtfm.csv. Podemos utilizar el análisis ‘Descriptivo’ de jamovi para confirmar que este conjunto de datos corresponde a un diseño equilibrado, con 2 observaciones para cada combinación de atención y lectura. De la misma forma también podemos calcular la nota media de cada combinación. Esto se muestra en Figure 14.16. Mirando las puntuaciones medias, una tiene la fuerte impresión de que leer el texto y asistir a la clase importan mucho.
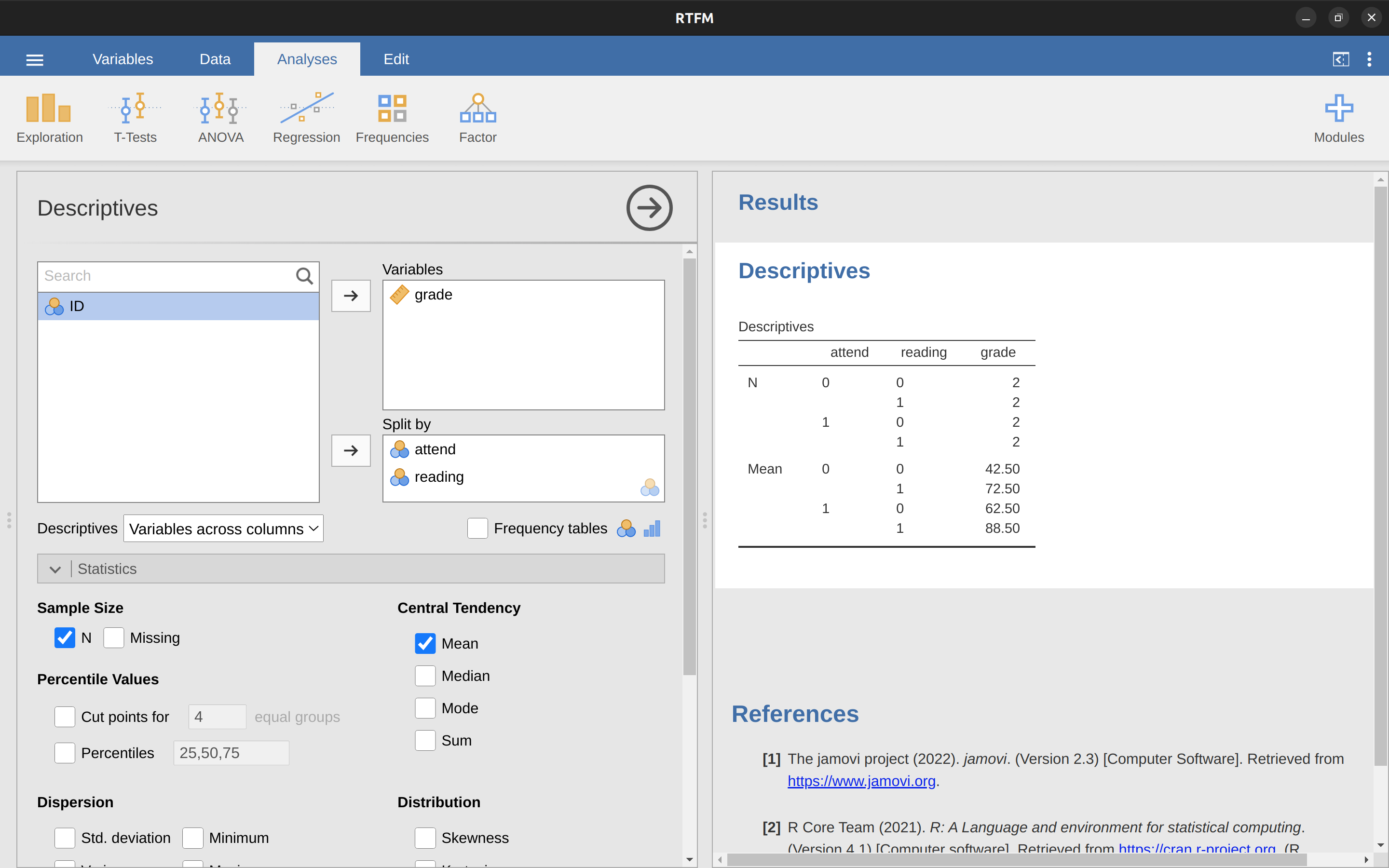
14.6.2 ANOVA con factores binarios como modelo de regresión
Bien, volvamos a hablar de las matemáticas. Ahora tenemos nuestros datos expresados en términos de tres variables numéricas: la variable continua \(Y\) y las dos variables binarias \(X_1\) y \(X_2\). Lo que quiero que reconozcas es que nuestro ANOVA factorial de \(2 \times 2\) es exactamente equivalente al modelo de regresión
\[Y_p=b_0+b_1 X_{1p} + b_2 X_{2p} + \epsilon_p\]
¡Esta es, por supuesto, exactamente la misma ecuación que usé anteriormente para describir un modelo de regresión de dos predictores! La única diferencia es que \(X_1\) y \(X_2\) ahora son variables binarias (es decir, los valores solo pueden ser 0 o 1), mientras que en un análisis de regresión esperamos que \(X_1\) y \(X_2\) sean continuos. Hay un par de formas en las que podría tratar de convencerte de esto. Una posibilidad sería hacer un largo ejercicio matemático demostrando que los dos son idénticos. Sin embargo, voy a arriesgarme y supongo que la mayoría de las lectoras de este libro lo encontrarán molesto en lugar de útil. En su lugar, explicaré las ideas básicas y luego confiaré en jamovi para mostrar que los análisis ANOVA y los análisis de regresión no solo son similares, sino que son idénticos a todos los efectos. Comencemos ejecutando esto como un ANOVA. Para hacer esto, usaremos el conjunto de datos rtfm y Figure 14.17 muestra lo que obtenemos cuando ejecutamos el análisis en jamovi.
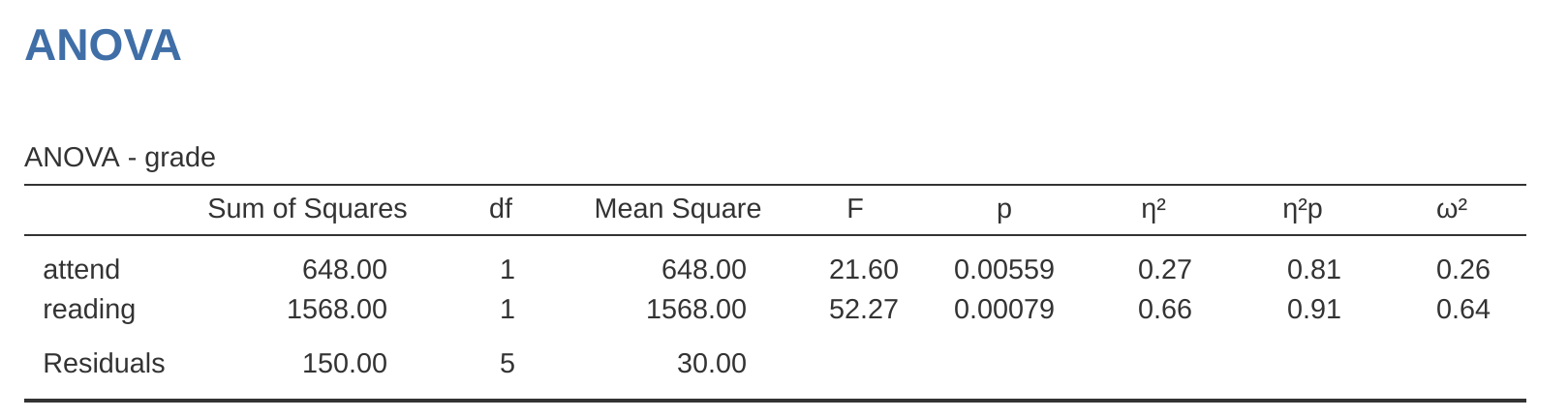
Entonces, al leer los números clave de la tabla ANOVA y las puntuaciones medias que presentamos anteriormente, podemos ver que los estudiantes obtuvieron una calificación más alta si asistieron a clase (\(F_{1,5} = 21.6, p = .0056\) ) y si leen el libro de texto (\(F_{1,5} = 52.3, p = .0008\)). Anotemos esos valores p y esos estadísticos \(F\).
Ahora pensemos en el mismo análisis desde una perspectiva de regresión lineal. En el conjunto de datos de rtfm, hemos codificado la asistencia y la lectura como si fueran predictores numéricos. En este caso, esto es perfectamente aceptable. Realmente hay un sentido en el que un estudiante que se presenta a clase (es decir, atiende = 1) de hecho ha tenido “más asistencia” que un estudiante que no lo hace (es decir, atiende = 0). Por lo tanto, no es nada irrazonable incluirlo como predictor en un modelo de regresión. Es un poco inusual, porque el predictor solo tiene dos valores posibles, pero no viola ninguno de los supuestos de la regresión lineal. Y es fácil de interpretar. Si el coeficiente de regresión para asistir es mayor que 0 significa que los estudiantes que asisten a clases obtienen calificaciones más altas. Si es menor que cero, los estudiantes que asisten a clases obtienen calificaciones más bajas. Lo mismo es cierto para nuestra variable de lectura.
Sin embargo, espera un segundo. ¿Por qué es esto cierto? Es algo que es intuitivamente obvio para todos los que han recibido algunas clases de estadísticas y se sienten cómodos con las matemáticas, pero no está claro para todos los demás a primera vista. Para ver por qué esto es cierto, ayuda mirar de cerca a algunos estudiantes específicos. Comencemos por considerar a los estudiantes de 6.º y 7.º en nuestro conjunto de datos (es decir, \(p = 6\) y \(p = 7\)). Ninguno ha leído el libro de texto, por lo que en ambos casos podemos poner lectura = 0. O, para decir lo mismo en nuestra notación matemática, observamos \(X_{2,6} = 0\) y \(X_{2,7} = 0\). Sin embargo, el estudiante número 7 sí se presentó a las clases (es decir, asistió = 1, \(X_{1,7} = 1\)) mientras que el estudiante número 6 no lo hizo (es decir, asistió = 0, \(X_{1,6} = 0\)). Ahora veamos qué sucede cuando insertamos estos números en la fórmula general de nuestra línea de regresión. Para el estudiante número 6, la regresión predice que
\[ \begin{split} \hat{Y}_6 & = b_0 + b_1 X_{1,6} + b_2 X_{2,6} \\ & = b_0 + (b_1 \times 0) + (b_2 \times 0) \\ & = b_0 \end{split} \]
Entonces, esperamos que este estudiante obtenga una calificación correspondiente al valor del término de intersección \(b_0\). ¿Qué pasa con el estudiante 7? Esta vez, cuando insertamos los números en la fórmula de la línea de regresión, obtenemos lo siguiente
\[ \begin{split} \hat{Y}_7 & = b_0 + b_1 X_{1,7} + b_2 X_{2,7} \\ & = b_0 + (b_1 \times 1) + (b_2 \times 0) \\ & = b_0 + b_1 \end{split} \]
Debido a que este estudiante asistió a clase, la calificación pronosticada es igual al término de intersección b0 más el coeficiente asociado con la variable de asistencia, \(b_1\). Entonces, si \(b_1\) es mayor que cero, esperamos que los estudiantes que asistan a las clases obtengan calificaciones más altas que los estudiantes que no lo hagan. Si este coeficiente es negativo, esperamos lo contrario: los estudiantes que asisten a clase terminan rindiendo mucho peor. De hecho, podemos llevar esto un poco más lejos. ¿Qué pasa con el estudiante número 1, que apareció en clase (\(X_{1,1} = 1\)) y leyó el libro de texto (\(X_{2,1} = 1\))? Si reemplazamos estos números en la regresión obtenemos
\[ \begin{split} \hat{Y}_1 & = b_0 + b_1 X_{1,1} + b_2 X_{2,1} \\ & = b_0 + (b_1 \times 1) + (b_2 \times 1) \\ & = b_0 + b_1 + b_2 \end{split} \]
Entonces, si asumimos que asistir a clase te ayuda a obtener una buena calificación (es decir, \(b1 \> 0\)) y si asumimos que leer el libro de texto también te ayuda a obtener una buena calificación (es decir, \(b2 \> 0\)), entonces nuestra expectativa es que el estudiante 1 obtenga una calificación más alta que el estudiante 6 y el estudiante 7.
Y en este punto no te sorprenderá saber que el modelo de regresión predice que el estudiante 3, que leyó el libro pero no asistió a las clases, obtendrá una calificación de \(b_{2} + b_{0}\). No os aburriré con otra fórmula de regresión. En su lugar, lo que haré es mostrarte Table 14.9 con las calificaciones esperadas.
| read textbook | |||
|---|---|---|---|
| no | yes | ||
| attended? | no | \( \beta_0 \) | \( \beta_0 + \beta_2 \) |
| yes | \( \beta_0 + \beta_1 \) | \( \beta_0 + \beta_1 + \beta_2 \) |
Como puedes ver, el término de intercepción \(b_0\) actúa como una especie de calificación “de referencia” que esperaría de aquellos estudiantes que no se toman el tiempo para asistir a clase o leer el libro de texto. De manera similar, \(b_1\) representa el impulso que se espera que obtengas si asistes a clase, y \(b_2\) representa el impulso que proviene de leer el libro de texto. De hecho, si se tratara de un ANOVA, es posible que quieras caracterizar b1 como el efecto principal de la asistencia y \(b_2\) como el efecto principal de la lectura. De hecho, para un ANOVA simple de \(2 \times 2\), así es exactamente como funciona.
Bien, ahora que realmente comenzamos a ver por qué ANOVA y la regresión son básicamente lo mismo, ejecutemos nuestra regresión usando los datos de rtfm y el análisis de regresión jamovi para convencernos de que esto es realmente cierto. Ejecutar la regresión de la manera habitual da los resultados que se muestran en Figure 14.18.

Hay algunas cosas interesantes a tener en cuenta aquí. Primero, fíjate que el término de intersección es 43,5, que está cerca de la media del “grupo” de 42,5 observada para esos dos estudiantes que no leyeron el texto ni asistieron a clase. En segundo lugar, observa que tenemos el coeficiente de regresión de \(b_1 = 18.0\) para la variable de asistencia, lo que sugiere que aquellos estudiantes que asistieron a clase obtuvieron una puntuación un 18% más alta que aquellos que no asistieron. Entonces, nuestra expectativa sería que aquellos estudiantes que asistieron a clase pero no leyeron el libro de texto obtuvieran una calificación de \(b_0 + b_1\), que es igual a \(43.5 + 18.0 = 61.5\). Puedes comprobar por ti misma que sucede lo mismo cuando miramos a los alumnos que leen el libro de texto.
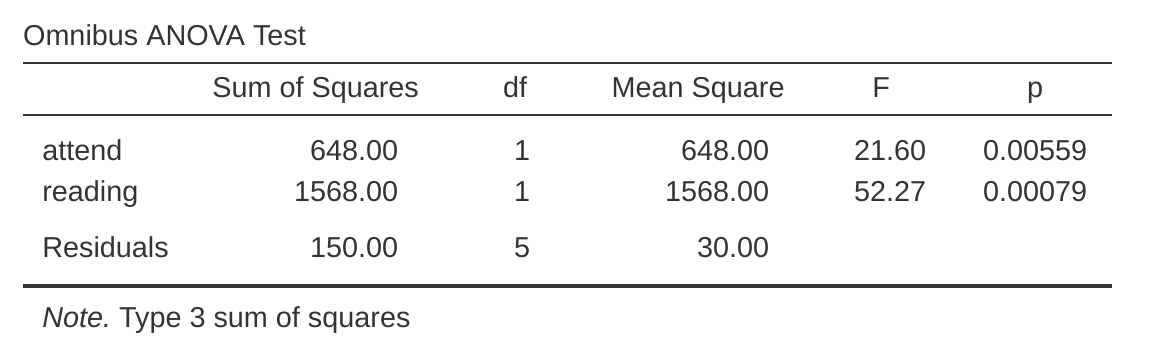
En realidad, podemos ir un poco más allá al establecer la equivalencia de nuestro ANOVA y nuestra regresión. Mira los valores p asociados con la variable de asistencia y la variable de lectura en el resultado de la regresión. Son idénticos a los que encontramos anteriormente cuando ejecutamos el ANOVA. Esto puede parecer un poco sorprendente, ya que la prueba utilizada al ejecutar nuestro modelo de regresión calcula un estadístico t y el ANOVA calcula un estadístico F. Sin embargo, si puedes recordar todo el camino de regreso a Chapter 7, mencioné que existe una relación entre la distribución t y la distribución F. Si tienes una cantidad que se distribuye de acuerdo con una distribución t con k grados de libertad y la elevas al cuadrado, entonces esta nueva cantidad al cuadrado sigue una distribución F cuyos grados de libertad son 1 y k. Podemos verificar esto con respecto a los estadísticos t en nuestro modelo de regresión. Para la variable de atención obtenemos un valor de 4,65. Si elevamos al cuadrado este número, obtenemos 21,6, que coincide con el estadístico F correspondiente en nuestro ANOVA.
Finalmente, una última cosa que debes saber. Debido a que jamovi comprende el hecho de que ANOVA y la regresión son ejemplos de modelos lineales, te permite extraer la tabla ANOVA clásica de su modelo de regresión utilizando la ‘Regresión lineal’ - ‘Coeficientes del modelo’ - ‘Prueba ómnibus’ - ‘Prueba ANOVA’, y esto te dará la tabla que se muestra en Figure 14.19.
14.6.3 Cómo codificar factores no binarios como contrastes
En este punto, te mostré cómo podemos ver un ANOVA de \(2 \times 2\) en un modelo lineal. Y es bastante fácil ver cómo esto se generaliza a un ANOVA de \(2 \times 2 \times 2\) o un ANOVA de \(2 \times 2 \times 2 \times 2\). Es lo mismo, de verdad. Simplemente agrega una nueva variable binaria para cada uno de sus factores. Donde comienza a ser más complicado es cuando consideramos factores que tienen más de dos niveles. Considera, por ejemplo, el ANOVA de \(3 \times 2\) que ejecutamos anteriormente en este capítulo utilizando los datos de Clinicaltrial.csv. ¿Cómo podemos convertir el factor de fármacos de tres niveles en una forma numérica que sea apropiada para una regresión?
La respuesta a esta pregunta es bastante simple, en realidad. Todo lo que tenemos que hacer es darnos cuenta de que un factor de tres niveles se puede reescribir como dos variables binarias. Supongamos, por ejemplo, que yo fuera a crear una nueva variable binaria llamada druganxifree. Siempre que la variable fármacos sea igual a “anxifree” ponemos druganxifree = 1. De lo contrario, ponemos druganxifree = 0. Esta variable establece un contraste, en este caso entre anxifree y los otros dos fármacos. Por sí solo, por supuesto, el contraste druganxifree no es suficiente para capturar completamente toda la información en nuestra variable de fármacos. Necesitamos un segundo contraste, uno que nos permita distinguir entre el joyzepam y el placebo. Para ello, podemos crear un segundo contraste binario, llamado drugjoyzepam, que vale 1 si el fármaco es joyzepam y 0 si no lo es. En conjunto, estos dos contrastes nos permiten discriminar perfectamente entre los tres posibles fármacos. Table 14.10 ilustra esto.
| drug | druganxifree | drugjoyzepam |
|---|---|---|
| "placebo" | 0 | 0 |
| "anxifree" | 1 | 0 |
| "joyzepam" | 0 | 1 |
Si el fármaco administrado a un paciente es un placebo, las dos variables de contraste serán iguales a 0. Si el fármaco es Anxifree, la variable druganxifree será igual a 1, y la variable drugjoyzepam será 0. Lo contrario es cierto para Joyzepam: drugjoyzepam es 1 y druganxifree es 0.
Crear variables de contraste no es demasiado difícil usando la instrucción calcular nueva variable en jamovi. Por ejemplo, para crear la variable Anxifree, escribe esta expresión lógica en el cuadro de fórmula de calcular nueva variable: IF (drug == ‘Anxifree’, 1, 0)‘. De manera similar, para crear la nueva variable drugjoyzepam usa esta expresión lógica: IF(drug == ’joyzepam’, 1, 0). Del mismo modo para la terapia CBT: IF(terapia == ‘TCC’, 1, 0). Puedes ver estas nuevas variables y las expresiones lógicas correspondientes en el archivo de datos jamoviclinicaltrial2.omv.
Ahora hemos recodificado nuestro factor de tres niveles en términos de dos variables binarias y ya hemos visto que ANOVA y la regresión se comportan de la misma manera para las variables binarias. Sin embargo, existen algunas complejidades adicionales que surgen en este caso, que analizaremos en la siguiente sección.
14.6.4 La equivalencia entre ANOVA y regresión para factores no binarios
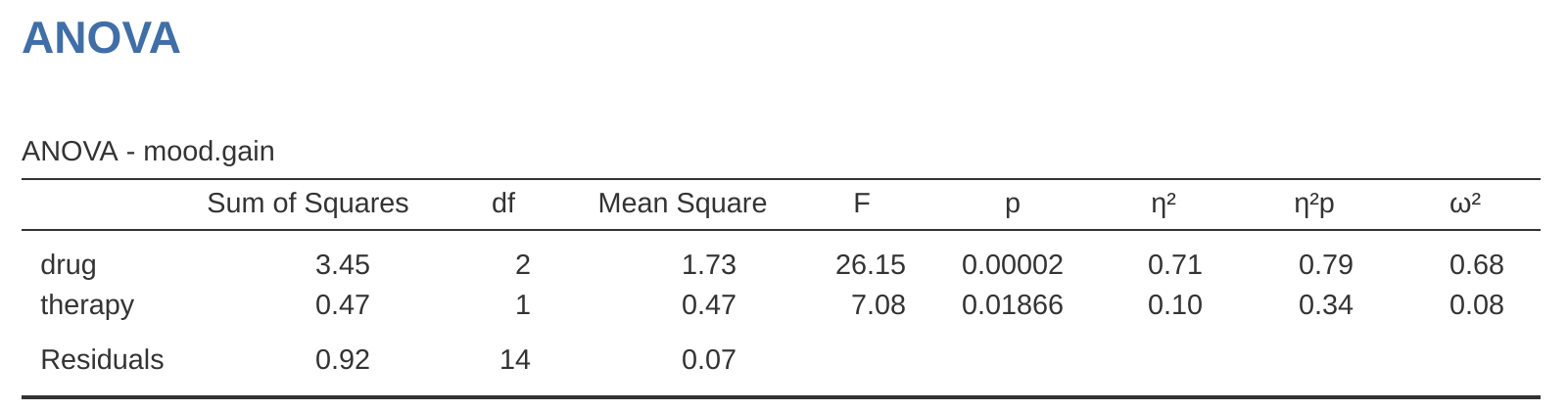
Ahora tenemos dos versiones diferentes del mismo conjunto de datos. Nuestros datos originales en los que la variable de fármaco del archivo Clinicaltrial.csv se expresa como un único factor de tres niveles, y los datos expandidos clinicaltrial2.omv en los que se expande en dos contrastes binarios. Una vez más, lo que queremos demostrar es que nuestro ANOVA factorial original de \(3 \times 2\) es equivalente a un modelo de regresión aplicado a las variables de contraste. Comencemos por volver a ejecutar el ANOVA, con los resultados que se muestran en Figure 14.20.
Obviamente, aquí no hay sorpresas. Ese es exactamente el mismo ANOVA que ejecutamos antes. A continuación, hagamos una regresión usando druganxifree, drugjoyzepam y terapia TCC como predictores. Los resultados se muestran en Figure 14.21.
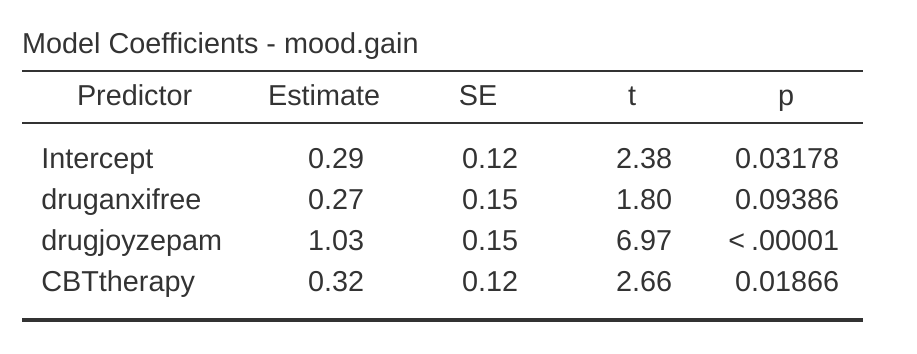
Mmm. Este no es el mismo resultado que obtuvimos la última vez. No es sorprendente que la salida de la regresión imprima los resultados de cada uno de los tres predictores por separado, tal como lo hizo cada vez que realizamos un análisis de regresión. Por un lado, podemos ver que el valor p para la variable TCC es exactamente el mismo que el del factor de terapia en nuestro ANOVA original, por lo que podemos estar seguras de que el modelo de regresión está haciendo lo mismo que hizo el ANOVA. Por otro lado, este modelo de regresión está probando el contraste druganxifree y el contraste drugjoyzepam por separado, como si fueran dos variables completamente independientes. Por supuesto, no es sorprendente, porque el pobre análisis de regresión no tiene forma de saber que drugjoyzepam y druganxifree son en realidad los dos contrastes diferentes que usamos para codificar nuestro factor de farmacos de tres niveles. Por lo que se sabe, Drugjoyzepam y Druganxifree no están más relacionados entre sí que Drugjoyzepam y TerapiaTCC. Sin embargo, tú y yo lo sabemos mejor. En este punto no estamos en absoluto interesadas en determinar si estos dos contrastes son individualmente significativos. Solo queremos saber si hay un efecto “general” del fármaco. Es decir, lo que queremos que haga jamovi es ejecutar algún tipo de prueba de “comparación de modelos”, una en la que los dos contrastes “relacionados con los fármacos” se agrupan para el propósito de la prueba. ¿Te suenoa? Todo lo que tenemos que hacer es especificar nuestro modelo nulo, que en este caso incluiría el predictor de la terapia TCC y omitiría las dos variables relacionadas con el fármaco, como en Figure 14.22.

Ah, eso está mejor. Nuestro estadístico F es 26,15, los grados de libertad son 2 y 14, y el valor p es 0,00002. Los números son idénticos a los que obtuvimos para el efecto principal del fármaco en nuestro ANOVA original. Una vez más vemos que ANOVA y regresión son esencialmente lo mismo. Ambos son modelos lineales y la maquinaria estadística subyacente en ANOVA es idéntica a la maquinaria utilizada en la regresión. La importancia de este hecho no debe ser subestimada. A lo largo del resto de este capítulo vamos a basarnos en gran medida en esta idea.
Aunque analizamos todas las complicaciones de calcular nuevas variables en jamovi para los contrastes druganxifree y drugjoyzepam, solo para mostrar que ANOVA y la regresión son esencialmente lo mismo, en el análisis de regresión lineal de jamovi hay un ingenioso atajo para obtener estos contrastes, ver Figure 14.23. Lo que jamovi está haciendo aquí es permitirte introducir las variables predictoras que son factores como, espera… ¡factores! Inteligente, eh. También puedes especificar qué grupo usar como nivel de referencia, a través de la opción ‘Niveles de referencia’. Hemos cambiado esto a ‘placebo’ y ‘no.terapia’, respectivamente, porque tiene más sentido.

Si también haces clic en la casilla de verificación de la prueba ‘ANOVA’ en la opción ‘Coeficientes del modelo’ - ‘Prueba ómnibus’, vemos que el estadístico F es 26,15, los grados de libertad son 2 y 14, y el valor p es 0,00002 (Figure 14.23). Los números son idénticos a los que obtuvimos para el efecto principal del fármaco en nuestro ANOVA original. Una vez más, vemos que ANOVA y regresión son esencialmente lo mismo. Ambos son modelos lineales y la maquinaria estadística subyacente en ANOVA es idéntica a la maquinaria utilizada en la regresión.
14.6.5 Grados de libertad como recuento de parámetros
Por fin, finalmente puedo dar una definición de grados de libertad con la que estoy contenta. Los grados de libertad se definen en términos del número de parámetros que deben estimarse en un modelo. Para un modelo de regresión o ANOVA, el número de parámetros corresponde al número de coeficientes de regresión (es decir, valores b), incluida la intersección. Teniendo en cuenta que cualquier prueba F siempre es una comparación entre dos modelos y el primer gl es la diferencia en la cantidad de parámetros. Por ejemplo, en la comparación de modelos anterior, el modelo nulo (mood.gain ~ terapiaCBT) tiene dos parámetros: hay un coeficiente de regresión para la variable terapiaCBT y otro para la intersección. El modelo alternativo (mood.gain ~ druganxifree + drugjoyzepam + therapyCBT) tiene cuatro parámetros: un coeficiente de regresión para cada uno de los tres contrastes y uno más para la intersección. Entonces, los grados de libertad asociados con la diferencia entre estos dos modelos son \(df_1 = 4 - 2 = 2\).
¿Qué pasa cuando no parece haber un modelo nulo? Por ejemplo, podrías estar pensando en la prueba F que aparece cuando seleccionas ‘Prueba F’ en las opciones ‘Regresión lineal’ - ‘Ajuste del modelo’. Originalmente lo describí como una prueba del modelo de regresión en su conjunto. Sin embargo, eso sigue siendo una comparación entre dos modelos. El modelo nulo es el modelo trivial que solo incluye 1 coeficiente de regresión, para el término de intersección. El modelo alternativo contiene \(K + 1\) coeficientes de regresión, uno para cada una de las K variables predictoras y uno más para la intersección. Entonces, el valor de gl que ves en esta prueba F es igual a \(df_1 = K + 1 - 1 = K\).
¿Qué pasa con el segundo valor de gl que aparece en la prueba F? Esto siempre se refiere a los grados de libertad asociados con los residuales. También es posible pensar en esto en términos de parámetros, pero de una manera un poco contraria a la intuición. Piensa en esto, de esta manera. Supón que el número total de observaciones en todo el estudio es N. Si quieres describir perfectamente cada uno de estos valores N, debes hacerlo usando, bueno… N números. Cuando creas un modelo de regresión, lo que realmente estás haciendo es especificar que algunos de los números deben describir perfectamente los datos. Si tu modelo tiene \(K\) predictores y una intersección, entonces has especificado \(K + 1\) números. Entonces, sin molestarte en averiguar exactamente cómo se haría esto, ¿cuántos números más crees que se necesitarán para transformar un modelo de regresión de parámetros K `1 en una redescripción perfecta de los datos sin procesar? Si te encuentras pensando que \((K + 1) + (N - K - 1) = N\), por lo que la respuesta tendría que ser \(N - K - 1\), ¡bien hecho! Eso es correcto. En principio, puedes imaginar un modelo de regresión absurdamente complicado que incluye un parámetro para cada punto de datos y, por supuesto, proporcionaría una descripción perfecta de los datos. Este modelo contendría \(N\) parámetros en total, pero estamos interesadas en la diferencia entre la cantidad de parámetros necesarios para describir este modelo completo (es decir, \(N\)) y la cantidad de parámetros utilizados por el modelo de regresión más simple en el que estás realmente interesada (es decir, \(K +1\)), por lo que el segundo grado de libertad en la prueba F es \(df_2 = N - K - 1\), donde K es el número de predictores (en un modelo de regresión) o el número de contrastes (en un ANOVA). En el ejemplo anterior, hay \((N = 18\) observaciones en el conjunto de datos y \(K + 1 = 4\) coeficientes de regresión asociados con el modelo ANOVA, por lo que los grados de libertad de los residuales son \(df_2 = 18 - 4 = 14\).
14.7 Diferentes formas de especificar contrastes
En la sección anterior, te mostré un método para convertir un factor en una colección de contrastes. En el método que te mostré, especificamos un conjunto de variables binarias en las que definimos una tabla como Table 14.11.
| drug | druganxifree | drugjoyzepam |
|---|---|---|
| "placebo" | 0 | 0 |
| "anxifree" | 1 | 0 |
| "joyzepam" | 0 | 1 |
Cada fila de la tabla corresponde a uno de los niveles de los factores, y cada columna corresponde a uno de los contrastes. Esta tabla, que siempre tiene una fila más que columnas, tiene un nombre especial. Se llama matriz de contraste. Sin embargo, hay muchas formas diferentes de especificar una matriz de contraste. En esta sección, discuto algunas de las matrices de contraste estándar que usan los estadísticos y cómo puedes usarlas en jamovi. Si planeas leer la sección sobre [ANOVA factorial 3: diseños no balanceados] más adelante, vale la pena leer esta sección detenidamente. Si no, puedes pasarla por alto, porque la elección de los contrastes no importa mucho para los diseños equilibrados.
14.7.1 Contrastes de tratamiento
En el tipo particular de contrastes que he descrito anteriormente, un nivel del factor es especial y actúa como una especie de categoría de “línea base” (es decir, placebo en nuestro ejemplo), frente a la cual se definen los otros dos. El nombre de este tipo de contrastes es contrastes de tratamiento, también conocidos como “codificación ficticia”. En este contraste, cada nivel del factor se compara con un nivel de referencia base, y el nivel de referencia base es el valor de la intersección.
El nombre refleja el hecho de que estos contrastes son bastante naturales y sensibles cuando una de las categorías de su factor es realmente especial porque en realidad representa una línea base. Eso tiene sentido en nuestro ejemplo de ensayo clínico. La condición de placebo corresponde a la situación en la que no le das a la gente ningún fármaco real, por lo que es especial. Las otras dos condiciones se definen en relación con el placebo. En un caso reemplazas el placebo con Anxifree, y en el otro caso lo reemplazas con Joyzepam.
La tabla que se muestra arriba es una matriz de contrastes de tratamiento para un factor que tiene 3 niveles. Pero supongamos que quiero una matriz de contrastes de tratamiento para un factor con 5 niveles. Establecería esto como Table 14.12.
| Level | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
| 5 | 0 | 0 | 0 | 1 |
En este ejemplo, el primer contraste es el nivel 2 comparado con el nivel 1, el segundo contraste es el nivel 3 comparado con el nivel 1, y así sucesivamente. Ten en cuenta que, de forma predeterminada, el primer nivel del factor siempre se trata como la categoría de referencia (es decir, es el que tiene todo ceros y no tiene un contraste explícito asociado). En jamovi, puedes cambiar qué categoría es el primer nivel del factor manipulando el orden de los niveles de la variable que se muestra en la ventana ‘Variable de datos’ (haz doble clic en el nombre de la variable en la columna de la hoja de cálculo para que aparezca la Vista de variables de datos.
14.7.2 Contrastes Helmert
Los contrastes de tratamiento son útiles para muchas situaciones. Sin embargo, tienen más sentido en la situación en la que realmente hay una categoría de referencia y quieres evaluar todos los demás grupos en relación con esa. En otras situaciones, sin embargo, no existe tal categoría de referencia y puede tener más sentido comparar cada grupo con la media de los otros grupos. Aquí es donde nos encontramos con los contrastes de Helmert, generados por la opción ‘helmert’ en el cuadro de selección jamovi ‘ANOVA’ - ‘Contrastes’. La idea que subyace a los contrastes de Helmert es comparar cada grupo con la media de los “anteriores”. Es decir, el primer contraste representa la diferencia entre el grupo 2 y el grupo 1, el segundo contraste representa la diferencia entre el grupo 3 y la media de los grupos 1 y 2, y así sucesivamente. Esto se traduce en una matriz de contraste que se parece a Table 14.13 para un factor con cinco niveles.
| 1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| 2 | 1 | -1 | -1 | -1 |
| 3 | 0 | 2 | -1 | -1 |
| 4 | 0 | 0 | 3 | -1 |
| 5 | 0 | 0 | 0 | 4 |
Algo útil acerca de los contrastes de Helmert es que cada contraste suma cero (es decir, todas las columnas suman cero). Esto tiene como consecuencia que, cuando interpretamos el ANOVA como una regresión, el término de la intersección corresponde a la media general \(\mu_{..}\) si estamos usando contrastes de Helmert. Compara esto con los contrastes de tratamiento, en los que el término de intersección corresponde a la media del grupo para la categoría de referencia. Esta propiedad puede ser muy útil en algunas situaciones. Lo que hemos estado asumiendo hasta ahora no es tan importante si tienes un diseño balanceado, pero será importante más adelante cuando consideremos [diseños no balanceados] (ANOVA factorial: diseños no balanceados). De hecho, la razón principal por la que me he molestado en incluir esta sección es que los contrastes se vuelven importantes si quieres entender el ANOVA no balanceado.
14.7.3 Contrastes de suma a cero
La tercera opción que debo mencionar brevemente son los contrastes de “suma a cero”, llamados contrastes “simples” en jamovi, que se utilizan para construir comparaciones por pares entre grupos. En concreto, cada contraste codifica la diferencia entre uno de los grupos y una categoría base, que en este caso corresponde al primer grupo (Table 14.14).
| 1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
| 5 | 0 | 0 | 0 | 1 |
Al igual que los contrastes de Helmert, vemos que cada columna suma cero, lo que significa que el término de intersección corresponde a la media general cuando ANOVA se trata como un modelo de regresión. Al interpretar estos contrastes, lo que hay que reconocer es que cada uno de estos contrastes es una comparación por pares entre el grupo 1 y uno de los otros cuatro grupos. Específicamente, el contraste 1 corresponde a una comparación de “grupo 2 menos grupo 1”, el contraste 2 corresponde a una comparación de “grupo 3 menos grupo 1”, y así sucesivamente.8
14.7.4 Contrastes opcionales en jamovi
jamovi también viene con una variedad de opciones que pueden generar diferentes tipos de contrastes en ANOVA. Estos se pueden encontrar en la opción ‘Contrastes’ en la ventana principal de análisis de ANOVA, donde se enumeran los tipos de contraste en Table 14.15:
| Contrast type | |
|---|---|
| Deviation | Compares the mean of each level (except a reference category) to the mean of all of the levels (grand mean) |
| Simple | Like the treatment contrasts, the simple contrast compares the mean of each level to the mean of a specified level. This type of contrast is useful when there is a control group. By default the first category is the reference. However, with a simple contrast the intercept is the grand mean of all the levels of the factors. |
| Difference | Compares the mean of each level (except the first) to the mean of previous levels. (Sometimes called reverse Helmert contrasts) |
| Helmert | Compares the mean of each level of the factor (except the last) to the mean of subsequent levels |
| Repeated | Compares the mean of each level (except the last) to the mean of the subsequent level |
| Polynomial | Compares the linear effect and quadratic effect. The first degree of freedom contains the linear effect across all categories; the second degree of freedom, the quadratic effect. These contrasts are often used to estimate polynomial trends |
14.8 Pruebas post hoc
Es hora de cambiar a un tema diferente. En lugar de comparaciones planificadas previamente que hayas probado utilizando contrastes, supongamos que has realizado tu ANOVA y resulta que obtuviste algunos efectos significativos. Debido al hecho de que las pruebas F son pruebas “ómnibus” que realmente solo prueban la hipótesis nula de que no hay diferencias entre los grupos, la obtención de un efecto significativo no indica qué grupos son diferentes de otros. Discutimos este problema en Chapter 13, y en ese capítulo nuestra solución fue ejecutar pruebas t para todos los pares de grupos posibles, haciendo correcciones para comparaciones múltiples (por ejemplo, Bonferroni, Holm) para controlar la tasa de error de tipo I en todas las comparaciones. Los métodos que usamos en Chapter 13 tienen la ventaja de ser relativamente simples y ser el tipo de herramientas que puedes usar en muchas situaciones diferentes en las que estás probando múltiples hipótesis, pero no son necesariamente las mejores opciones si estás interesada en realizar pruebas post hoc eficientes en un contexto ANOVA. En realidad, hay muchos métodos diferentes para realizar comparaciones múltiples en la literatura estadística (Hsu, 1996), y estaría fuera del alcance de un texto introductorio como este discutirlos todos en detalle.
Dicho esto, hay una herramienta sobre la que quiero llamar tu atención, a saber, la “Diferencia honestamente significativa” de Tukey, o HSD de Tukey para abreviar. Por una vez, te ahorraré las fórmulas y me limitaré a las ideas cualitativas. La idea básica en el HSD de Tukey es examinar todas las comparaciones por pares relevantes entre grupos, y solo es realmente apropiado usar el HSD de Tukey si lo que te interesa son las diferencias por pares.9 Por ejemplo, antes realizaste un ANOVA factorial usando el conjunto de datos clinictrial.csv, y donde especificamos un efecto principal para el fármaco y un efecto principal para la terapia, estaríamos interesados en las siguientes cuatro comparaciones:
- La diferencia en el estado de ánimo de las personas que recibieron Anxifree frente a las personas que recibieron el placebo.
- La diferencia en el estado de ánimo de las personas que recibieron Joyzepam versus las personas que recibieron el placebo.
- La diferencia en el estado de ánimo de las personas que recibieron Anxifree frente a las personas que recibieron Joyzepam.
- La diferencia en el aumento del estado de ánimo para las personas tratadas con TCC y las personas que no recibieron terapia.
Para cualquiera de estas comparaciones, estamos interesadas en la verdadera diferencia entre las medias de los grupos (población). El HSD de Tukey construye intervalos de confianza simultáneos para las cuatro comparaciones. Lo que queremos decir con un intervalo de confianza “simultáneo” del 95 % es que, si tuviéramos que repetir este estudio muchas veces, entonces en el 95 % de los resultados del estudio, los intervalos de confianza contendrían el valor verdadero relevante. Además, podemos usar estos intervalos de confianza para calcular un valor p ajustado para cualquier comparación específica.
La función TukeyHSD en jamovi es bastante fácil de usar. Simplemente especifica el término del modelo ANOVA para el que deseas ejecutar las pruebas post hoc. Por ejemplo, si buscáramos ejecutar pruebas post hoc para los efectos principales pero no para la interacción, abriríamos la opción ‘Pruebas Post Hoc’ en la pantalla de análisis de ANOVA, moverías las variables del fármaco y la terapia al recuadro de la derecha, y luego seleccionas la casilla de verificación ‘Tukey’ en la lista de posibles correcciones post hoc que podrían aplicarse. Esto, junto con la tabla de resultados correspondiente, se muestra en Figure 14.24.

El resultado que se muestra en la tabla de resultados de ‘Pruebas post hoc’ es (espero) bastante sencillo. La primera comparación, por ejemplo, es la diferencia de Anxifree versus placebo, y la primera parte del resultado indica que la diferencia observada en las medias de los grupos es .27. El siguiente número es el error estándar de la diferencia, a partir del cual podríamos calcular el intervalo de confianza del 95 % si quisiéramos, aunque jamovi actualmente no ofrece esta opción. Luego hay una columna con los grados de libertad, una columna con el valor t y finalmente una columna con el valor p. Para la primera comparación, el valor p ajustado es .21. En cambio, si nos fijamos en la siguiente línea, vemos que la diferencia observada entre el joyzepam y el placebo es de 1,03, y este resultado es significativo (p < 0,001).
Hasta aquí todo bien. ¿Qué pasa si tu modelo incluye términos de interacción? Por ejemplo, la opción predeterminada en jamovi es permitir la posibilidad de que exista una interacción entre el fármaco y la terapia. Si ese es el caso, la cantidad de comparaciones por pares que debemos considerar comienza a aumentar. Como antes, necesitamos considerar las tres comparaciones que son relevantes para el efecto principal del fármaco y la única comparación que es relevante para el efecto principal de la terapia. Pero, si queremos considerar la posibilidad de una interacción significativa (y tratar de encontrar las diferencias de grupo que sustentan esa interacción significativa), debemos incluir comparaciones como las siguientes:
- La diferencia en el aumento del estado de ánimo de las personas que recibieron Anxifree y recibieron tratamiento con TCC, en comparación con las personas que recibieron el placebo y recibieron tratamiento con TCC
- La diferencia en el estado de ánimo de las personas que recibieron Anxifree y no recibieron terapia, en comparación con las personas que recibieron el placebo y no recibieron terapia.
- etc
Hay muchas de estas comparaciones que debes considerar. Entonces, cuando ejecutamos el análisis post hoc de Tukey para este modelo ANOVA, vemos que ha realizado muchas comparaciones por pares (19 en total), como se muestra en Figure 14.25. Puedes ver que es bastante similar al anterior, pero con muchas más comparaciones.

14.9 El método de las comparaciones planificadas
Siguiendo con las secciones anteriores sobre contrastes y pruebas post hoc en ANOVA, creo que el método de comparaciones planificadas es lo suficientemente importante como para merecer una breve discusión. En nuestras discusiones sobre comparaciones múltiples, en la sección anterior y en Chapter 13, supuse que las pruebas que deseas ejecutar son genuinamente post hoc. Por ejemplo, en nuestro ejemplo de fármacos anterior, tal vez pensaste que todos los fármacos tendrían efectos diferentes en el estado de ánimo (es decir, planteaste la hipótesis de un efecto principal del fármaco), pero no tenías ninguna hipótesis específica sobre cómo serían las diferencias, ni tenías una idea real sobre qué comparaciones por pares valdría la pena mirar. Si ese es el caso, entonces realmente tiens que recurrir a algo como el HSD de Tukey para hacer tus comparaciones por pares.
Sin embargo, la situación es bastante diferente si realmente tuvieras hipótesis reales y específicas sobre qué comparaciones son de interés, y nunca tuvieras la intención de ver otras comparaciones además de las que especificaste con anticipación. Cuando esto es cierto, y si te apegas honesta y rigurosamente a tus nobles intenciones de no realizar ninguna otra comparación (incluso cuando los datos parezcan mostrarte efectos deliciosamente significativos para cosas para las que no tenías una prueba de hipótesis), entonces realmente no tiene mucho sentido ejecutar algo como el HSD de Tukey, porque hace correcciones para un montón de comparaciones que nunca te importaron y nunca tuviste la intención de mirar. En esas circunstancias, puedes ejecutar con seguridad una cantidad (limitada) de pruebas de hipótesis sin realizar un ajuste para pruebas múltiples. Esta situación se conoce como método de comparaciones planificadas, y en ocasiones se utiliza en ensayos clínicos. Sin embargo, la consideración adicional está fuera del alcance de este libro introductorio, ¡pero al menos que sepas que este método existe!
14.10 ANOVA factorial 3: diseños no equilibrados
Es útil conocer el ANOVA factorial. Ha sido una de las herramientas estándar utilizadas para analizar datos experimentales durante muchas décadas, y descubrirás que no puede leer más de dos o tres artículos de psicología sin encontrarte con un ANOVA en alguna parte. Sin embargo, hay una gran diferencia entre los ANOVA que verás en muchos artículos científicos reales y los ANOVA que he descrito hasta ahora. En la vida real, rara vez tenemos la suerte de tener diseños perfectamente equilibrados. Por una razón u otra, es típico terminar con más observaciones en algunas celdas que en otras. O, dicho de otro modo, tenemos un diseño desequilibrado.
Los diseños desequilibrados deben tratarse con mucho más cuidado que los diseños equilibrados, y la teoría estadística que los sustenta es mucho más confusa. Puede ser una consecuencia de este desorden, o puede ser la falta de tiempo, pero mi experiencia ha sido que las clases de métodos de investigación de grado en psicología tienen una desagradable tendencia a ignorar este problema por completo. Muchos libros de texto de estadísticas también tienden a pasarlo por alto. El resultado de esto, creo, es que muchos investigadores activos en el campo en realidad no saben que hay varios “tipos” diferentes de ANOVA desequilibrados, y producen respuestas bastante diferentes. De hecho, al leer la literatura psicológica, me sorprende un poco el hecho de que la mayoría de las personas que informan los resultados de un ANOVA factorial desequilibrado en realidad no ofrecen suficientes detalles para reproducir el análisis. Secretamente sospecho que la mayoría de las personas ni siquiera se dan cuenta de que su paquete de software estadístico está tomando muchas decisiones de análisis de datos sustantivos en su nombre. En realidad, es un poco aterrador cuando lo piensas. Entonces, si quieres evitar entregar el control de tu análisis de datos a un software estúpido, sigue leyendo.
14.10.1 Los datos del café
Como es habitual, nos servirá para trabajar con algunos datos. El archivo coffee.csv contiene un conjunto de datos hipotéticos que produce un ANOVA desequilibrado de \(3 \times 2\). Supongamos que estuviéramos interesadas en averiguar si la tendencia de las personas a balbucear cuando toman demasiado café es puramente un efecto del café en sí, o si hay algún efecto de la leche y el azúcar que las personas agregan al café. Supongamos que llevamos a 18 personas y les damos un poco de café para beber. La cantidad de café/cafeína se mantuvo constante y variamos si se agregó leche o no, por lo que la leche es un factor binario con dos niveles, “sí” y “no”. También variamos el tipo de azúcar involucrado. El café podría contener azúcar “real” o podría contener azúcar “falsa” (es decir, edulcorante artificial) o podría contener “ninguna”, por lo que la variable azúcar es un factor de tres niveles. Nuestra variable de resultado es una variable continua que presumiblemente se refiere a alguna medida psicológicamente sensible de la medida en que alguien está “balbuceando”. Los detalles realmente no importan para nuestro propósito. Echa un vistazo a los datos en la vista de hoja de cálculo jamovi, como en Figure 14.26.
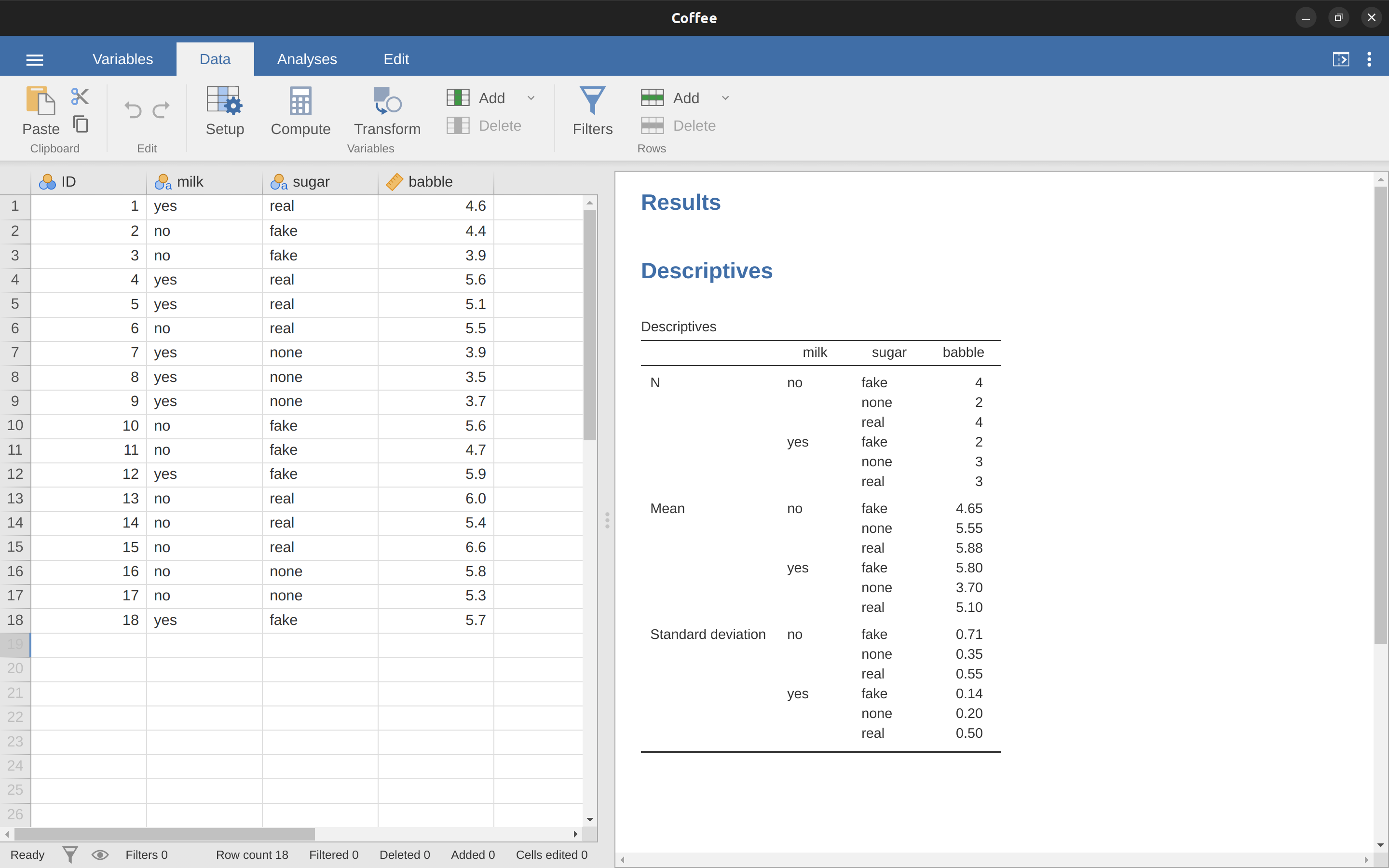
Mirando la tabla de medias en Figure 14.26 tenemos una fuerte impresión de que hay diferencias entre los grupos. Esto es especialmente cierto cuando comparamos estas medias con las desviaciones estándar de la variable balbuceo. Entre los grupos, esta desviación estándar varía de 0,14 a 0,71, que es bastante pequeña en relación con las diferencias en las medias de los grupos.10 Si bien al principio esto puede parecer un ANOVA factorial sencillo, un problema surge cuando miramos cuántas observaciones tenemos en cada grupo. Fíjate en las diferentes N para los diferentes grupos que se muestran en Figure 14.26. Esto viola una de nuestras suposiciones originales, a saber, que el número de personas en cada grupo es el mismo. Realmente no hemos discutido cómo manejar esta situación.
14.10.2 El “ANOVA estándar” no existe para diseños desequilibrados
Los diseños desequilibrados nos llevan al descubrimiento un tanto inquietante de que en realidad no hay nada a lo que podamos referirnos como un ANOVA estándar. De hecho, resulta que hay tres formas fundamentalmente diferentes11 en las que es posible que quieras ejecutar un ANOVA en un diseño desequilibrado. Si tienes un diseño equilibrado, las tres versiones producen resultados idénticos, con sumas de cuadrados, valores F, etc., todos conformes a las fórmulas que di al comienzo del capítulo. Sin embargo, cuando tu diseño está desequilibrado, no dan los mismos resultados. Además, no todos son igualmente apropiados para cada situación. Algunos métodos serán más apropiados para tu situación que otros. Dado todo esto, es importante comprender cuáles son los diferentes tipos de ANOVA y en qué se diferencian entre sí.
El primer tipo de ANOVA se conoce convencionalmente como suma de cuadrados tipo I. Estoy segura de que puedes adivinar cómo se llaman los otros dos. La parte de “suma de cuadrados” del nombre fue introducida por el paquete de software estadístico SAS y se ha convertido en una nomenclatura estándar, pero es un poco engañosa en algunos aspectos. Creo que la lógica para referirse a ellos como diferentes tipos de suma de cuadrados es que, cuando miras las tablas ANOVA que producen, la diferencia clave en los números son los valores SC. Los grados de libertad no cambian, los valores de MC aún se definen como SC dividido por df, etc. Sin embargo, la terminología es incorrecta porque oculta la razón por la cual los valores de SC son diferentes entre sí. Con ese fin, es mucho más útil pensar en los tres tipos diferentes de ANOVA como tres estrategias de prueba de hipótesis diferentes. Estas diferentes estrategias conducen a diferentes valores de SC, sin duda, pero lo importante aquí es la estrategia, no los valores de SC en sí mismos. Recuerda de la sección ANOVA como modelo lineal que cualquier prueba F en particular se considera mejor como una comparación entre dos modelos lineales. Entonces, cuando miras una tabla ANOVA, es útil recordar que cada una de esas pruebas F corresponde a un par de modelos que se están comparando. Por supuesto, esto lleva naturalmente a la pregunta de qué par de modelos se está comparando. Esta es la diferencia fundamental entre ANOVA Tipos I, II y III: cada uno corresponde a una forma diferente de elegir los pares de modelos para las pruebas.
14.10.3 Suma de Cuadrados Tipo I
El método Tipo I a veces se denomina suma de cuadrados “secuencial”, porque implica un proceso de agregar términos al modelo de uno en uno. Considera los datos del café, por ejemplo. Supongamos que queremos ejecutar el ANOVA factorial completo de \(3 \times 2\), incluidos los términos de interacción. El modelo completo contiene la variable de resultado balbuceo, las variables predictoras azúcar y leche, y el término de interacción azúcar \(\times\) leche. Esto se puede escribir como \(balbuceo \sum azúcar + leche + azúcar {\times} leche\). La estrategia Tipo I construye este modelo secuencialmente, comenzando desde el modelo más simple posible y agregando términos gradualmente.
El modelo más simple posible para los datos sería uno en el que se suponga que ni la leche ni el azúcar tienen ningún efecto sobre el balbuceo. El único término que se incluiría en dicho modelo es la intersección, escrito como balbuceo ~ 1. Esta es nuestra hipótesis nula inicial. El siguiente modelo más simple para los datos sería uno en el que solo se incluye uno de los dos efectos principales. En los datos del café, hay dos opciones diferentes posibles, porque podríamos elegir agregar leche primero o azúcar primero. El orden realmente importa, como veremos más adelante, pero por ahora hagamos una elección arbitraria y escojamos azúcar. Entonces, el segundo modelo en nuestra secuencia de modelos es balbuceo ~ azúcar, y forma la hipótesis alternativa para nuestra primera prueba. Ahora tenemos nuestra primera prueba de hipótesis (Table 14.16).
| Null model: | \(babble \sim 1\) |
|---|---|
| Alternative model: | \(babble \sim sugar\) |
Esta comparación forma nuestra prueba de hipótesis del efecto principal del azúcar. El siguiente paso en nuestro ejercicio de construcción de modelos es agregar el otro término de efecto principal, por lo que el siguiente modelo en nuestra secuencia es balbuceo ~ azúcar + leche. Luego, la segunda prueba de hipótesis se forma comparando el siguiente par de modelos (Table 14.17).
| Null model: | \(babble \sim sugar\) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk\) |
Esta comparación forma nuestra prueba de hipótesis del efecto principal de la leche. En cierto sentido, este enfoque es muy elegante: la hipótesis alternativa de la primera prueba forma la hipótesis nula de la segunda. Es en este sentido que el método Tipo I es estrictamente secuencial. Cada prueba se basa directamente en los resultados de la última. Sin embargo, en otro sentido es muy poco elegante, porque hay una fuerte asimetría entre las dos pruebas. La prueba del efecto principal del azúcar (la primera prueba) ignora por completo la leche, mientras que la prueba del efecto principal de la leche (la segunda prueba) sí tiene en cuenta el azúcar. En cualquier caso, el cuarto modelo de nuestra secuencia ahora es el modelo completo, balbuceo ~ azúcar + leche + azúcar \(\times\) leche, y la prueba de hipótesis correspondiente se muestra en Table 14.18.
| Null model: | \(babble \sim sugar + milk\) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk + sugar * milk \) |
El método de prueba de hipótesis predeterminado utilizado por jamovi ANOVA es la suma de cuadrados Tipo III, por lo que para ejecutar un análisis de suma de cuadrados Tipo I, debemos seleccionar ‘Tipo 1’ en el cuadro de selección ‘Suma de cuadrados’ en las opciones de jamovi ‘ANOVA’ - Opciones de ‘Modelo’. Esto nos da la tabla ANOVA que se muestra en Figure 14.27.
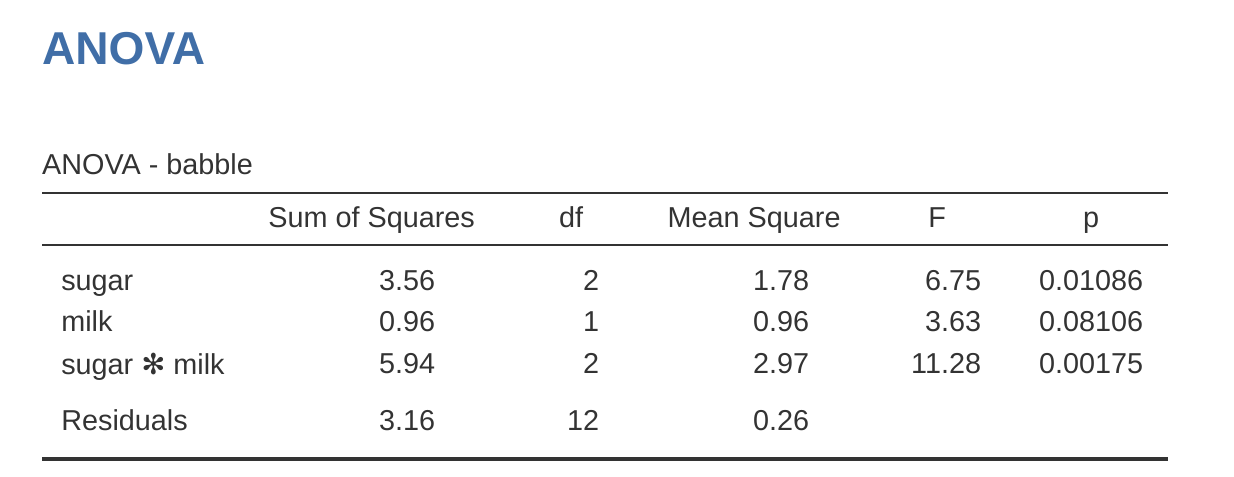
El gran problema con el uso de la suma de cuadrados Tipo I es el hecho de que realmente depende del orden en que ingresas las variables. Sin embargo, en muchas situaciones el investigador no tiene motivos para preferir un orden sobre otro. Este es presumiblemente el caso de nuestro problema de la leche y el azúcar. ¿Deberíamos agregar primero la leche o primero el azúcar? Es exactamente tan arbitrario como una pregunta de análisis de datos que como una pregunta de preparación de café. De hecho, puede haber algunas personas con opiniones firmes sobre el orden, pero es difícil imaginar una respuesta de principios a la pregunta. Sin embargo, mira lo que sucede cuando cambiamos el orden, como en Figure 14.28.
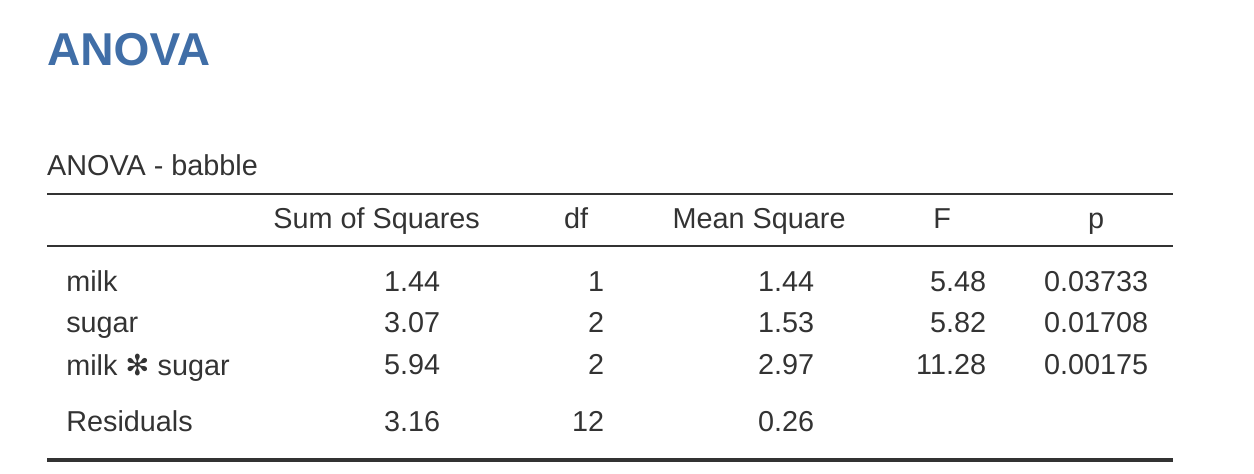
Los valores p para ambos términos del efecto principal han cambiado, y de forma bastante drástica. Entre otras cosas, el efecto de la leche se ha vuelto significativo (aunque se debe evitar sacar conclusiones firmes al respecto, como mencioné anteriormente). ¿Cuál de estos dos ANOVA debe informarse? No es obvio de inmediato.
Cuando observas las pruebas de hipótesis que se utilizan para definir el “primer” efecto principal y el “segundo”, está claro que son cualitativamente diferentes entre sí. En nuestro ejemplo inicial, vimos que la prueba del efecto principal del azúcar ignora por completo la leche, mientras que la prueba del efecto principal de la leche sí tiene en cuenta el azúcar. Como tal, la estrategia de prueba Tipo I realmente trata el primer efecto principal como si tuviera una especie de primacía teórica sobre el segundo. En mi experiencia, muy rara vez hay primacía teórica de este tipo que justifique tratar cualquiera de los dos efectos principales de forma asimétrica.
La consecuencia de todo esto es que las pruebas de Tipo I rara vez son de mucho interés, por lo que deberíamos pasar a hablar de las pruebas de Tipo II y las pruebas de Tipo III.
14.10.4 Suma de Cuadrados Tipo III
Habiendo terminado de hablar sobre las pruebas de Tipo I, podrías pensar que lo más natural a hacer a continuación sería hablar sobre las pruebas de Tipo II. Sin embargo, creo que en realidad es un poco más natural discutir las pruebas de Tipo III (que son simples y predeterminadas en jamovi ANOVA) antes de hablar de las pruebas de Tipo II (que son más complicadas). La idea básica que subyace a las pruebas de Tipo III es extremadamente simple. Independientemente del término que intentes evaluar, ejecuta la prueba F en la que la hipótesis alternativa corresponde al modelo ANOVA completo según lo especificado por el usuario, y el modelo nulo simplemente elimina ese término que estás probando. Por ejemplo, en el ejemplo del café, en el que nuestro modelo completo era balbuceo ~ azúcar + leche + azúcar \(\times\) leche, la prueba del efecto principal del azúcar correspondería a una comparación entre los siguientes dos modelos (Table 14.19).
| Null model: | \(babble \sim milk + sugar * milk\) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk +sugar * milk \) |
De manera similar, el efecto principal de la leche se evalúa probando el modelo completo contra un modelo nulo que elimina el término leche, como en Table 14.20.
| Null model: | \(babble \sim sugar + sugar * milk\) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk +sugar * milk \) |
Finalmente, el término de interacción azúcar \(\times\) leche se evalúa exactamente de la misma manera. Una vez más, probamos el modelo completo con un modelo nulo que elimina el término de interacción azúcar \(\times\) leche, como en Table 14.21.
| Null model: | \(babble \sim sugar + milk\) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk +sugar * milk \) |
La idea básica se generaliza a ANOVA de orden superior. Por ejemplo, supongamos que intentáramos ejecutar un ANOVA con tres factores, A, B y C, y deseáramos considerar todos los efectos principales posibles y todas las interacciones posibles, incluida la interacción de tres vías A \(\times\) B $$ C. (Table 14.22) te muestra cómo son las pruebas de Tipo III para esta situación).
| Term being tested is | Null model is outcome ~ ... | Alternative model is outcome ~ ... |
|---|---|---|
| A | \(B + C + A*B + A*C + B*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
| B | \(A + C + A*B + A*C + B*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C\) |
| C | \(A + B + A*B + A*C + B*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
| A*B | \(A + B + C + A*C + B*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
| A*C | \(A + B + C + A*B + B*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
| B*C | \(A + B + C + A*B + A*C + A*B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
| A*B*C | \(A + B + C + A*B + A*C + B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
Por fea que parezca esa tabla, es bastante simple. En todos los casos, la hipótesis alternativa corresponde al modelo completo que contiene tres términos de efectos principales (p. ej., A), tres interacciones de dos vías (p. ej., A*B) y una interacción de tres vías (p. ej., A*B* C)). El modelo nulo siempre contiene 6 de estos 7 términos, y el que falta es aquel cuyo significado estamos tratando de probar.
A primera vista, las pruebas de Tipo III parecen una buena idea. En primer lugar, eliminamos la asimetría que nos causaba problemas al ejecutar las pruebas de Tipo I. Y como ahora estamos tratando todos los términos de la misma manera, los resultados de las pruebas de hipótesis no dependen del orden en que los especifiquemos. Esto es definitivamente algo bueno. Sin embargo, existe un gran problema al interpretar los resultados de las pruebas, especialmente para los términos de efecto principal. Considera los datos del café. Supongamos que resulta que el efecto principal de la leche no es significativo según las pruebas de Tipo III. Lo que esto nos dice es que balbucear ~ azúcar + azúcar*leche es un modelo mejor para los datos que el modelo completo. Pero, ¿qué significa eso? Si el término de interacción azúcar*leche tampoco fuera significativo, estaríamos tentados a concluir que los datos nos dicen que lo único que importa es el azúcar. Pero supongamos que tenemos un término de interacción significativo, pero un efecto principal no significativo de la leche. En este caso, ¿debemos suponer que realmente hay un “efecto del azúcar”, una “interacción entre la leche y el azúcar”, pero no un “efecto de la leche”? Eso parece una locura. La respuesta correcta simplemente debe ser que no tiene sentido12 hablar sobre el efecto principal si la interacción es significativa. En general, esto parece ser lo que la mayoría de los estadísticos nos aconsejan hacer, y creo que ese es el consejo correcto. Pero si realmente no tiene sentido hablar de efectos principales no significativos en presencia de una interacción significativa, entonces no es del todo obvio por qué las pruebas de Tipo III deben permitir que la hipótesis nula se base en un modelo que incluye la interacción pero omite una de los principales efectos que lo componen. Cuando se caracterizan de esta manera, las hipótesis nulas realmente no tienen mucho sentido.
Más adelante, veremos que las pruebas de Tipo III se pueden canjear en algunos contextos, pero primero echemos un vistazo a la tabla de resultados de ANOVA usando la suma de cuadrados de Tipo III, consulta Figure 14.29.

Pero ten en cuenta que una de las características perversas de la estrategia de prueba de Tipo III es que, por lo general, los resultados dependen de los contrastes que utilizas para codificar tus factores (consulta la sección Diferentes formas de especificar contrastes si has olvidado cuáles son los diferentes tipos de contrastes).13
De acuerdo, si los valores de p que normalmente surgen de los análisis de Tipo III (pero no en jamovi) son tan sensibles a la elección de los contrastes, ¿significa eso que las pruebas de Tipo III son esencialmente arbitrarias y no fiables? Hasta cierto punto, eso es cierto, y cuando pasemos a una discusión sobre las pruebas de Tipo II, veremos que los análisis de Tipo II evitan esta arbitrariedad por completo, pero creo que es una conclusión demasiado firme. En primer lugar, es importante reconocer que algunas elecciones de contrastes siempre producirán las mismas respuestas (ah, esto es lo que sucede en jamovi). De particular importancia es el hecho de que si las columnas de nuestra matriz de contraste están todas restringidas para sumar cero, entonces el análisis Tipo III siempre dará las mismas respuestas.
En las pruebas de Tipo II veremos que los análisis de Tipo II evitan esta arbitrariedad por completo, pero creo que es una conclusión demasiado fuerte. En primer lugar, es importante reconocer que algunas elecciones de contrastes siempre producirán las mismas respuestas (ah, esto es lo que sucede en jamovi). De particular importancia es el hecho de que si las columnas de nuestra matriz de contraste están todas restringidas para sumar cero, entonces el análisis Tipo III siempre dará las mismas respuestas.
14.10.5 Suma de Cuadrados Tipo II
Bien, ahora hemos visto las pruebas Tipo I y III, y ambas son bastante sencillas. Las pruebas de tipo I se realizan agregando gradualmente los términos uno a la vez, mientras que las pruebas de tipo III se realizan tomando el modelo completo y observando qué sucede cuando eliminas cada término. Sin embargo, ambos pueden tener algunas limitaciones. Las pruebas de tipo I dependen del orden en que ingresas los términos, y las pruebas de tipo III dependen de cómo codifiques tus contrastes. Las pruebas de tipo II son un poco más difíciles de describir, pero evitan ambos problemas y, como resultado, son un poco más fáciles de interpretar.
Las pruebas de tipo II son muy similares a las pruebas de tipo III. Comienzas con un modelo “completo” y pruebas un término en particular eliminándolo de ese modelo. Sin embargo, las pruebas de Tipo II se basan en el principio de marginalidad que establece que no debes omitir un término de orden inferior de tu modelo si hay términos de orden superior que dependen de él. Entonces, por ejemplo, si tu modelo contiene la interacción bidireccional A \(\times\) B (un término de segundo orden), entonces realmente deberías contener los efectos principales A y B (términos de primer orden). De manera similar, si contiene un término de interacción triple A \(\times\) B \(\times\) C, entonces el modelo también debe incluir los efectos principales A, B y C, así como las interacciones más simples A \(\times\) B, A \(\times\) C y B \(\times\) C. Las pruebas de tipo III violan rutinariamente el principio de marginalidad. Por ejemplo, considera la prueba del efecto principal de A en el contexto de un ANOVA de tres vías que incluye todos los términos de interacción posibles. De acuerdo con las pruebas Tipo III, nuestros modelos nulo y alternativo están en Table 14.23.
| Null model: | \(outcome \sim B + C + A*B + A*C + B*C + A*B*C\) |
|---|---|
| Alternative model: | \(outcome \sim A + B + C + A*B + A*C + B*C + A*B*C\) |
Fíjate que la hipótesis nula omite A, pero incluye A \(\times\) B, A \(\times\) C y A \(\times\) B \(\times\) C como parte del modelo. Esto, de acuerdo con las pruebas de Tipo II, no es una buena elección de hipótesis nula. En cambio, lo que deberíamos hacer, si queremos probar la hipótesis nula de que A no es relevante para nuestro resultado, es especificar la hipótesis nula que es el modelo más complicado que no se basa en ninguna forma de A, incluso como una interacción. La hipótesis alternativa corresponde a este modelo nulo más un término de efecto principal de A. Esto está mucho más cerca de lo que la mayoría de la gente pensaría intuitivamente como un “efecto principal de A”, y produce lo siguiente como nuestra prueba Tipo II del efecto principal de A (Table 14.24). 14
| Null model: | \(outcome \sim B + C + B*C\) |
|---|---|
| Alternative model: | \(outcome \sim A + B + C + B*C\) |
De todos modos, solo para darte una idea de cómo se desarrollan las pruebas Tipo II, aquí está la tabla completa (Table 14.25) de las pruebas que se aplicarían en un ANOVA factorial de tres vías:
| Term being tested is | Null model is outcome ~ ... | Alternative model is outcome ~ ... |
|---|---|---|
| A | \(B + C + B*C \) | \(A + B + C + B*C \) |
| B | \(A + C + A*C \) | \(A + B + C + A*C\) |
| C | \(A + B + A*B \) | \(A + B + C + A*B\) |
| A*B | \(A + B + C + A*C + B*C \) | \(A + B + C + A*B + A*C + B*C \) |
| A*C | \(A + B + C + A*B + B*C \) | \(A + B + C + A*B + A*C + B*C \) |
| B*C | \(A + B + C + A*B + A*C \) | \(A + B + C + A*B + A*C + B*C \) |
| A*B*C | \(A + B + C + A*B + A*C + B*C \) | \(A + B + C + A*B + A*C + B*C + A*B*C \) |
En el contexto del ANOVA de dos vías que hemos estado usando en los datos del café, las pruebas de hipótesis son aún más simples. El efecto principal del azúcar corresponde a una prueba F que compara estos dos modelos (Table 14.26).
| Null model: | \(babble \sim milk \) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk\) |
La prueba del efecto principal de la leche está en Table 14.27.
| Null model: | \(babble \sim sugar \) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk\) |
Finalmente, la prueba para la interacción azúcar \(\times\) leche está en Table 14.28.
| Null model: | \(babble \sim sugar + milk \) |
|---|---|
| Alternative model: | \(babble \sim sugar + milk + sugar*milk \) |
Ejecutar las pruebas vuelve a ser sencillo. Simplemente selecciona ‘Tipo 2’ en el cuadro de selección ‘Suma de cuadrados’ en las opciones jamovi ‘ANOVA’ - ‘Modelo’. Esto nos da la tabla ANOVA que se muestra en Figure 14.30.
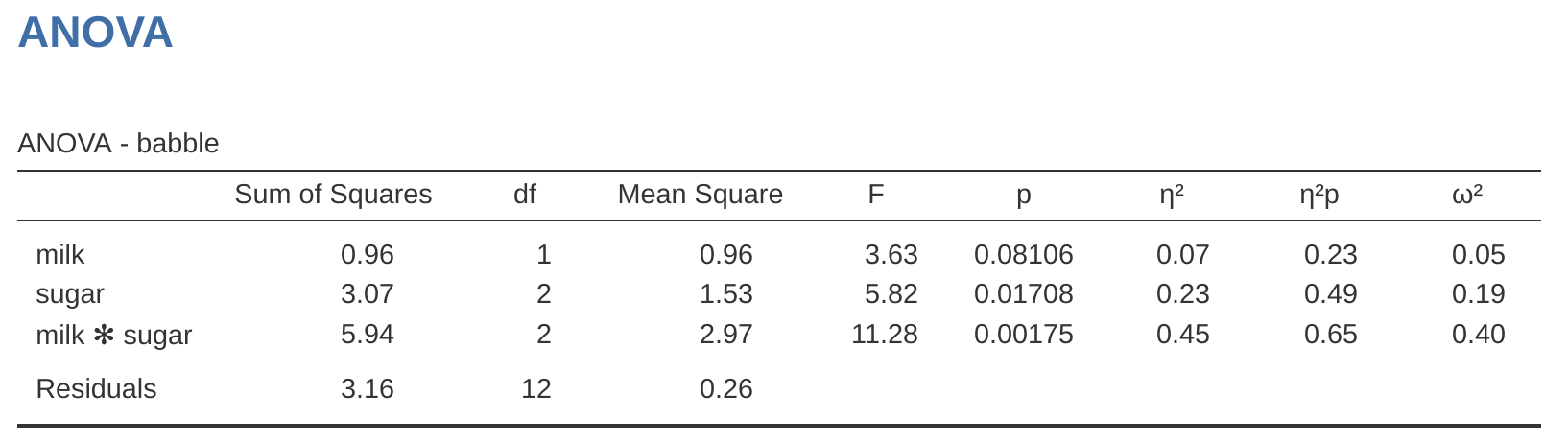
Las pruebas de tipo II tienen algunas ventajas claras sobre las pruebas de tipo I y tipo III. No dependen del orden en que especificas los factores (a diferencia del Tipo I), y no dependen de los contrastes que usas para especificar tus factores (a diferencia del Tipo III). Y aunque las opiniones pueden diferir sobre este último punto, y definitivamente dependerá de lo que intentes hacer con sus datos, creo que es más probable que las pruebas de hipótesis que especificas correspondan a algo que realmente te interese. Como consecuencia, encuentro que por lo general es más fácil interpretar los resultados de una prueba Tipo II que los resultados de una prueba Tipo I o Tipo III. Por esta razón, mi consejo tentativo es que, si no puedes pensar en ninguna comparación de modelos obvia que se corresponda directamente con tus preguntas de investigación, pero aun así deseas ejecutar un ANOVA en un diseño no balanceado, las pruebas de Tipo II son probablemente una mejor opción que las de Tipo I o Tipo III.15
14.10.6 Tamaños de los efectos (y sumas de cuadrados no aditivas)
jamovi también proporciona los tamaños de efecto \(\eta^2\) y \(\eta^2\) parcial cuando seleccionas estas opciones, como en Figure 14.30. Sin embargo, un diseño desequilibrado involucra un poco de complejidad adicional.
Si recuerdas nuestras primeras discusiones sobre ANOVA, una de las ideas clave que subyacen a los cálculos de sumas de cuadrados es que si sumamos todos los términos SC asociados con los efectos en el modelo, y lo sumamos a la SC residual, se supone que suman la suma de cuadrados total. Y, además de eso, la idea detrás de \(\eta^2\) es que, debido a que estás dividiendo uno de los términos de SC por el valor total de SC, un valor de \(\eta^2\) puede interpretarse como la proporción de la varianza explicada por un término particular. Pero esto no es tan sencillo en los diseños desequilibrados porque parte de la varianza “desaparece”.
Esto parece un poco extraño al principio, pero he aquí por qué. Cuando tienes diseños desequilibrados, tus factores se correlacionan entre sí, y se vuelve difícil distinguir la diferencia entre el efecto del Factor A y el efecto del Factor B. En el caso extremo, supon que ejecutaríamos un diseño $2 $ en el que el número de participantes en cada grupo había sido como en Table 14.29.
| sugar | no sugar | |
|---|---|---|
| milk | 100 | 0 |
| no milk | 0 | 100 |
Aquí tenemos un diseño espectacularmente desequilibrado: 100 personas tienen leche y azúcar, 100 personas no tienen leche ni azúcar, y eso es todo. Hay 0 personas con leche y sin azúcar y 0 personas con azúcar pero sin leche. Ahora imagina que, cuando recolectamos los datos, resultó que hay una gran diferencia (y estadísticamente significativa) entre el grupo “leche y azúcar” y el grupo “sin leche y sin azúcar”. ¿Es este un efecto principal del azúcar? ¿Un efecto principal de la leche? ¿O una interacción? Es imposible saberlo, porque la presencia de azúcar tiene una asociación perfecta con la presencia de leche. Ahora supongamos que el diseño hubiera sido un poco más equilibrado (Table 14.30).
| sugar | no sugar | |
|---|---|---|
| milk | 100 | 5 |
| no milk | 5 | 100 |
Esta vez, es técnicamente posible distinguir entre el efecto de la leche y el efecto del azúcar, porque algunas personas tienen uno pero no el otro. Sin embargo, seguirá siendo bastante difícil hacerlo, porque la asociación entre el azúcar y la leche sigue siendo extremadamente fuerte y hay muy pocas observaciones en dos de los grupos. Una vez más, es muy probable que estemos en una situación en la que sabemos que las variables predictoras (leche y azúcar) están relacionadas con el resultado (balbuceo), pero no sabemos si la naturaleza de esa relación es el efecto principal de un predictor u otro, o de la interacción.
14.11 Resumen
- [ANOVA factorial 1: diseños balanceados, sin interacciones] y con interacciones incluidas
- Tamaño del efecto, medias estimadas e intervalos de confianza en un ANOVA factorial
- [Comprobación de suposiciones] en ANOVA
- Análisis de Covarianza (ANCOVA)
- Entender [ANOVA como un modelo lineal], incluyendo Diferentes formas de especificar contrastes
- Pruebas post hoc utilizando el HSD de Tukey y un breve comentario sobre El método de las comparaciones planificadas
- [ANOVA factorial 3: diseños desequilibrados]
lo bueno de la notación de subíndices es que se generaliza muy bien. Si nuestro experimento hubiera involucrado un tercer factor, entonces podríamos simplemente agregar un tercer subíndice. En principio, la notación se extiende a tantos factores como desees incluir, pero en este libro rara vez consideraremos análisis que involucren más de dos factores y nunca más de tres.↩︎
técnicamente, la marginalización no es exactamente idéntica a una media normal. Es un promedio ponderado en el que se tiene en cuenta la frecuencia de los diferentes eventos sobre los que se está promediando. Sin embargo, en un diseño equilibrado, todas las frecuencias de nuestras celdas son iguales por definición, por lo que las dos son equivalentes. Discutiremos los diseños desequilibrados más adelante, y cuando lo hagamos, verás que todos nuestros cálculos se convierten en un verdadero dolor de cabeza. Pero ignoremos esto por ahora.↩︎
Ahora que tenemos nuestra notación correcta, podemos calcular los valores de la suma de cuadrados para cada uno de los dos factores de una manera relativamente familiar. Para el Factor A, nuestra suma de cuadrados entre grupos se calcula evaluando hasta qué punto las medias marginales (fila) \(\bar{Y}_{1.} , \bar{Y}_{2.}\), etc., son diferente de la media general \(\bar{Y}_{..}\) Hacemos esto de la misma manera que lo hicimos para ANOVA unifactorial: calcula la suma de la diferencia al cuadrado entre los valores \(\bar{Y}_{i .}\) y \(\bar{Y}_{..}\). Específicamente, si hay N personas en cada grupo, entonces calculamos \[SS_A=(N \times C)\sum_{r=1}^R (\bar{Y}_{r.}-\bar{Y }_{..})^2\] Al igual que con ANOVA unifactorial, la parte \(^a\) es la más interesante de esta fórmula, que corresponde a la desviación al cuadrado asociada con el nivel r. Lo que hace esta fórmula es calcular esta desviación al cuadrado para todos los niveles R del factor, sumarlos y luego multiplicar el resultado por \(N \times C\). La razón de esta última parte es que hay múltiples celdas en nuestro diseño que tienen nivel \(r\) en el Factor A. De hecho, hay C de ellas, una correspondiente a cada nivel posible del Factor B. Por ejemplo, en nuestro ejemplo hay dos celdas diferentes en el diseño correspondientes al fármaco sin ansiedad: una para personas sin terapia y otra para el grupo de TCC. Y mo solo eso, dentro de cada una de estas celdas hay N observaciones. Entonces, si queremos convertir nuestro valor SC en una cantidad que calcule la suma de cuadrados entre grupos “por observación”, tenemos que multiplicar por \(N \times C\). La fórmula para el factor \(B\) es, por supuesto, la mismo, solo que con algunos subíndices mezclados \[SS_B=(N \times R)\sum_{c=1}^C (\bar{Y}_{.c} -\bar{Y}_{..})^2\] Ahora que tenemos estas fórmulas, podemos compararlas con la salida jamovi de la sección anterior. Una vez más, unade hoja de cálculo es útil para este tipo de cálculos, así que pruébalo tú misma. También puedes echarle un vistazo a la versión que hice en Excel en el archivo clinictrial_factorialanova.xls. Primero, calculemos la suma de cuadrados asociada con el efecto principal del fármaco. Hay un total de \(N = 3\) personas en cada grupo y \(C = 2\) diferentes tipos de terapia. O, dicho de otro modo, hay \(3 \times 2 = 6\) personas que recibieron algún fármaco en particular. Cuando hacemos estos cálculos en una hoja de cálculo, obtenemos un valor de 3,45 para la suma de cuadrados asociada con el efecto principal del fármaco. No es sorprendente que este sea el mismo número que obtienes cuando buscas el valor SC para el factor de fármacos en la tabla ANOVA que presenté anteriormente, en Figure 14.3.
Podemos repetir el mismo tipo de cálculo para el efecto de la terapia. Nuevamente, hay \(N = 3\) personas en cada grupo, pero como hay \(R = 3\) medicamentos diferentes, esta vez notamos que hay \(3 \times 3 = 9\) personas que recibieron TCC y 9 personas adicionales que recibieron el placebo. Así que nuestro cálculo en este caso nos da un valor de \(0.47\) para la suma de cuadrados asociada con el efecto principal de la terapia. Una vez más, no nos sorprende ver que nuestros cálculos son idénticos a la salida de ANOVA en Figure 14.3.
Así es como se calculan los valores SC para los dos efectos principales. Estos valores SC son análogos a los valores de suma de cuadrados entre grupos que calculamos al hacer ANOVA unifactorial en Chapter 13. Sin embargo, ya no es una buena idea pensar en ellos como valores SC entre grupos, porque tenemos dos variables de agrupación diferentes y es fácil confundirse. Sin embargo, para construir una prueba \(F\), también necesitamos calcular la suma de cuadrados dentro de los grupos. De acuerdo con la terminología que usamos en Chapter 12 y la terminología que jamovi usa al imprimir la tabla ANOVA, comenzaré a referirme al valor SC dentro de los grupos como la suma de cuadrados residual \(SC_R\).
Creo que la manera más fácil de pensar en los valores de la SC residual en este contexto es pensar en ello como la variación sobrante en la variable de resultado después de tener en cuenta las diferencias en las medias marginales (es decir, después de eliminar \(SC_A\) y \(SC_B\)). Lo que quiero decir con eso es que podemos comenzar calculando la suma de cuadrados total, que etiquetaré como \(SC_T\). La fórmula para esto es más o menos la misma que para ANOVA unifactorial. Cogemos la diferencia entre cada observación Yrci y la media general \(\hat{Y}_{..}\), elevamos al cuadrado las diferencias y las sumamos todas \[SS_T=\sum_{r=1}^R \sum_{c =1}^C \sum_{i=1}^N (Y_{rci}-\bar{Y}_{..})^2\] La “suma triple” aquí parece más complicada de lo que es. En las dos primeras sumas, sumamos todos los niveles del Factor \(A\) (es decir, todas las filas r posibles de nuestra tabla) y todos los niveles del Factor \(B\) (es decir, todas las columnas posibles \(c\)). Cada combinación rc corresponde a un solo grupo y cada grupo contiene \(N\) personas, por lo que también tenemos que sumar todas esas personas (es decir, todos los valores de \(i\)). En otras palabras, todo lo que estamos haciendo aquí es sumar todas las observaciones en el conjunto de datos (es decir, todas las posibles combinaciones de rci). En este punto, conocemos la variabilidad total de la variable de resultado SCT y sabemos cuánto de esa variabilidad se puede atribuir al Factor A (\(SC_A\)) y cuánto se puede atribuir al Factor B (\(SC_B\)). La suma de cuadrados residual se define así como la variabilidad en \(Y\) que no se puede atribuir a ninguno de nuestros dos factores. En otras palabras, \[SS_R=SS_T-(SS_A+SS_B)\] Por supuesto, hay una fórmula que puedes usar para calcular la SC residual directamente, pero creo que tiene más sentido conceptual pensarlo así. El objetivo de llamarlo residual es que es la variación sobrante, y la fórmula anterior lo deja claro. También debo señalar que, de acuerdo con la terminología utilizada en el capítulo de regresión, es común referirse a \(SC_A + SC_B\) como la varianza atribuible al “modelo ANOVA”, denotado SCM, por lo que a menudo decimos que la suma de cuadrados total es igual a la suma de cuadrados modelo más la suma de cuadrados residual. Más adelante en este capítulo veremos que esto no es solo una similitud superficial: ANOVA y la regresión son en realidad lo mismo. En cualquier caso, probablemente valga la pena tomarse un momento para comprobar que podemos calcular \(SC_R\) usando esta fórmula y verificar que obtenemos la misma respuesta que produce jamovi en su tabla ANOVA. Los cálculos son bastante sencillos cuando se realizan en una hoja de cálculo (consulta el archivo clinictrial_factorialanova.xls). Podemos calcular la SC total usando las fórmulas anteriores (obteniendo una respuesta de \(SC total = 4.85\)) y luego la SC residual (= 0.92). Una vez más, obtenemos la misma respuesta.
—
\(^a\)Traducción al inglés: “menos tedioso”.↩︎Como consecuencia, la forma en que se formaliza la idea de un efecto de interacción en términos de hipótesis nula y alternativa es un poco difícil, y supongo que muchos de los lectores de este libro probablemente no están tan interesados. Aun así, intentaré ofrecer una idea básica. Para empezar, necesitamos ser un poco más explícitos acerca de nuestros efectos principales. Considera el efecto principal del Factor \(A\) (fármaco en nuestro ejemplo). Originalmente formulamos esto en términos de la hipótesis nula de que las dos medias marginales \(\mu_r\). son iguales entre si. Obviamente, si son iguales entre sí, entonces también deben ser iguales a la media general \(\mu_{..}\), ¿verdad? Entonces, lo que podemos hacer es definir el efecto del Factor \(A\) en el nivel \(r\) para que sea igual a la diferencia entre la media marginal \(\mu_{r.}\) y la media general \(\mu_{..}\). Denotemos este efecto por \(\alpha_r\), y observemos que \[\alpha_r=\mu_{r.}-\mu_{..}\] Ahora, por definición, todos los valores de \(\alpha_r\) deben sumar cero, por la misma razón que el promedio de las medias marginales \(\mu_c\) debe ser la media general \(\mu_{..}\). De manera similar, podemos definir el efecto del Factor B en el nivel i como la diferencia entre la media marginal de la columna \(\mu_{.c}\) y la media general \(\mu_{..}\) \[\beta_c=\mu_{. c}-\mu_{..}\] y una vez más, estos valores de \(\beta_c\) deben sumar cero. La razón por la que a veces a los estadísticos les gusta hablar de los efectos principales en términos de estos valores \(\alpha_r\) y \(\beta_c\) es que les permite ser precisos sobre lo que significa decir que no hay efecto de interacción. Si no hay interacción en absoluto, entonces estos valores \(\alpha_r\) y \(\beta_c\) describirán perfectamente las medias del grupo \(mu_{rc}\). Específicamente, significa que \[\mu_{rc}=\mu_{..}+\alpha_{r}+\beta_{c}\] Es decir, no hay nada especial en las medias grupales que no pudieras predecir conociendo las medias marginales. Y ahí está nuestra hipótesis nula. La hipótesis alternativa es que \[\mu_{rc} \neq \mu_{..}+\alpha_{r}+\beta_{c}\] para al menos un grupo \(rc\) en nuestra tabla. Sin embargo, a los estadísticos a menudo les gusta escribir esto de manera ligeramente diferente. Por lo general, definirán la interacción específica asociada con el grupo \(rc\) como un número, torpemente denominado \((\alpha \beta)_{rc}\), y luego dirán que la hipótesis alternativa es que \[\mu_{rc}=\mu_{..} +\alpha_{r} +\beta_{c} + (\alpha \beta )_{rc}\] donde \((\alpha \beta)_{rc}\) es distinto de cero para al menos un grupo. Esta notación es un poco fea a la vista, pero es útil, como veremos cuando analicemos cómo calcular la suma de cuadrados. ¿Cómo debemos calcular la suma de cuadrados para los términos de interacción, \(SS_{A:B}\)? Bueno, en primer lugar, es útil notar cómo acabamos de definir el efecto de interacción en términos de en qué medida las medias grupales difieren de lo que esperarías mirando sólo las medias marginales. Por supuesto, todas esas fórmulas se refieren a parámetros poblacionales en lugar de estadísticas muestrales, por lo que en realidad no sabemos cuáles son. Sin embargo, podemos estimarlos usando medias muestrales en lugar de medias poblacionales. Entonces, para el Factor \(A\), una buena manera de estimar el efecto principal en el nivel r es como la diferencia entre la media marginal muestral \(\bar{Y}_{rc}\) y la media general muestral \(\bar{Y}_{..}\) Es decir, usaríamos esto como nuestra estimación del efecto \[\hat{\alpha}_r = bar{Y}_{r.}-\bar{Y}_{..}\] De manera similar, nuestra estimación del efecto principal del Factor B en el nivel c se puede definir de la siguiente manera \[\hat{\beta}_{c}=\hat{Y}_{.c}-\bar{Y}_{..}\] Ahora, si vuelves a las fórmulas que usé para describir los valores de \(SC\) para los dos efectos principales, notarás que estos términos de efectos son exactamente las cantidades que estábamos elevando al cuadrado y sumando. Entonces, ¿cuál es el análogo de esto para los términos de interacción? La respuesta a esto la podemos encontrar primero reorganizando la fórmula para las medias grupales \(\mu_{rc}\) bajo la hipótesis alternativa, de modo que obtengamos \[\begin{aligned} (\alpha \beta)_{rc} & = \mu_{rc } - \mu_{..} - \alpha_r - \beta_c \\ & = \mu_{rc} - \mu_{..} - (\mu_{r.}-\mu_{..})-(\mu_ {.c}-\mu_{..}) \\ & = \mu_{rc} - \mu_{r.} - \mu_{.c} +\mu_{..} \end{aligned}\] Entonces , una vez más, si sustituimos nuestros estadísticos muestrales en lugar de las medias poblacionales, obtenemos lo siguiente como nuestra estimación del efecto de interacción para el grupo \(rc\), que es \[(\hat{\alpha \beta})_{rc }=\bar{Y}_{rc}-\hat{Y}_{r.}-\bar{Y}_{.c}+\bar{Y}_{..}\] Ahora lo que tenemos hacer es sumar todas estas estimaciones en todos los niveles de \(R\) del Factor \(A\) y todos los niveles de \(C\) del Factor \(B\), y obtenemos la siguiente fórmula para la suma de cuadrados asociados con la interacción como un todo \[SS_{A:B}=N \sum_{r=1}^R \sum_{c=1}^C (\bar{Y}_{rc}-\bar{Y}_{r.}-\ bar{Y}_{.c}+\bar{Y}_{..})^2\] donde multiplicamos por N porque hay N observaciones en cada uno de los grupos, y queremos que nuestros valores \(SC\) reflejen la variación entre observaciones explicada por la interacción, no la variación entre grupos. Ahora que tenemos una fórmula para calcular \(SS_{A:B}\), es importante reconocer que el término de interacción es parte del modelo (por supuesto), por lo que la suma de cuadrados total asociada con el modelo, SCM, ahora es igual a la suma de los tres valores SC relevantes, \(SC_A + SC_B + SC_{A:B}\). La suma de cuadrados residual SCR se define como la variación sobrante, a saber, \(SC_T - SC_M\), pero ahora que tenemos el término de interacción, se convierte en \[SS_R=SS_T-(SS_A+SS_B+SS_{A:B})\] Como consecuencia, la suma de cuadrados residual \(SS_R\) será menor que en nuestro ANOVA original que no incluía interacciones.↩︎
Es posible que ya hayas notado esto al mirar el análisis de efectos principales en jamovi que describimos anteriormente. Para el propósito de la explicación en este libro, eliminé el componente de interacción del modelo anterior para mantener las cosas limpias y sencillas.↩︎
este capítulo parece estar estableciendo un nuevo récord por la cantidad de cosas diferentes que puede representar la letra R. Hasta ahora tenemos R refiriéndose al paquete de software, el número de filas en nuestra tabla de medias, los residuales en el modelo y ahora el coeficiente de correlación en una regresión. Lo siento. Claramente no tenemos suficientes letras en el alfabeto. Sin embargo, me he esforzado mucho para dejar claro a qué se refiere R en cada caso.↩︎
Inverosímilmente grande, creo. ¡La artificialidad de este conjunto de datos realmente está comenzando a mostrarse!↩︎
¿Cuál es la diferencia entre el tratamiento y los contrastes simples, te escucho preguntar? Bueno, como ejemplo básico, considera un efecto principal de género, con \(m=0\) y \(f=1\). El coeficiente correspondiente al contraste de tratamientos medirá la diferencia de medias entre hombres y mujeres, y la intersección sería la media de los hombres. Sin embargo, con un contraste simple, es decir, \(m=-1\) y \(f=1\), la intersección es el promedio de las medias y el efecto principal es la diferencia de la media de cada grupo con respecto a la intersección.↩︎
si, por ejemplo, realmente estás interesada en saber si el Grupo A es significativamente diferente de la media del Grupo B y el Grupo C, entonces necesitas usar una herramienta diferente (por ejemplo, el método de Scheffe , que es más conservador y está fuera del alcance de este libro). Sin embargo, en la mayoría de los casos, probablemente estés interesada en las diferencias de grupos por parejas, por lo que es útil conocer el HSD de Tukey.↩︎
esta discrepancia en las desviaciones estándar podría (y debería) hacer que te preguntes si tenemos una violación del supuesto de homogeneidad de varianzas. Lo dejaré como un ejercicio para que el lector verifique esto usando la opción de prueba de Levene.↩︎
En realidad, esto es un poco mentira. Los ANOVA pueden variar de otras maneras además de las que he discutido en este libro. Por ejemplo, he ignorado por completo la diferencia entre los modelos de efectos fijos en los que los niveles de un factor son “fijos” por el experimentador o el mundo, y los modelos de efectos aleatorios en los que los niveles son muestras aleatorias de una población más grande de niveles posibles (este libro solo cubre modelos de efectos fijos). No cometas el error de pensar que este libro, o cualquier otro, te dirá “todo lo que necesitas saber” sobre estadística, más de lo que un solo libro podría decirte todo lo que necesitas saber sobre psicología, física o filosofía. La vida es demasiado complicada para que eso sea cierto. Sin embargo, esto no es motivo de desesperación. La mayoría de los investigadores se las arreglan con un conocimiento práctico básico de ANOVA que no va más allá que este libro. Solo quiero que tengas en cuenta que este libro es solo el comienzo de una historia muy larga, no la historia completa.↩︎
O, como mínimo, rara vez de interés.↩︎
Sin embargo, en jamovi los resultados para el ANOVA de suma de cuadrados Tipo III son los mismos independientemente del contraste seleccionado, ¡así que jamovi obviamente está haciendo algo diferente!↩︎
Ten en cuenta, por supuesto, que esto depende del modelo que especificó el usuario. Si el modelo ANOVA original no contiene un término de interacción para \(B \times C\), obviamente no aparecerá ni en el valor nulo ni en el alternativo. Pero eso es cierto para los Tipos I, II y III. Nunca incluyen ningún término que no hayas incluido, pero toman decisiones diferentes sobre cómo construir pruebas para los que sí incluiste.↩︎
me parece divertido notar que el valor predeterminado en R es Tipo I y el valor predeterminado en SPSS y jamovi es Tipo III. Ninguno de estos me atrae tanto. En relación con esto, encuentro deprimente que casi nadie en la literatura psicológica se moleste en informar qué tipo de pruebas realizaron, y mucho menos el orden de las variables (para el Tipo I) o los contrastes utilizados (para el Tipo III). A menudo tampoco informan qué software usaron. La única forma en que puedo entender lo que la gente suele informar es tratar de adivinar a partir de pistas auxiliares qué software estaban usando y asumir que nunca cambiaron la configuración predeterminada. ¡Por favor, no hagas esto! Ahora que conoces estos problemas, asegúrate de indicar qué software usaste y, si estás informando los resultados de ANOVA para datos desequilibrados, especifica qué Tipo de pruebas ejecutaste, especifica la información del orden de los factores si has realizado pruebas Tipo I y especifica contrastes si has hecho pruebas de tipo III. O, mejor aún, ¡haz pruebas de hipótesis que correspondan a las cosas que realmente te importan y luego infórmalas!↩︎