10 Análisis de datos categóricos

Ahora que hemos cubierto la teoría básica de las pruebas de hipótesis, es hora de comenzar a buscar pruebas específicas que se usan habitualmente en psicología. ¿Por dónde empezar? No todos los libros de texto se ponen de acuerdo sobre por dónde empezar, pero yo voy a empezar con “$\chi^2$ tests” (este capítulo, pronunciado “chi-square”¹ y ” pruebas t” en Chapter 11). Ambas herramientas se usan con mucha frecuencia en la práctica científica, y aunque no son tan potentes como la “regresión” y el “análisis de varianza” que trataremos en capítulos posteriores, son mucho más fáciles de entender.

El término “datos categóricos” no es más que otro nombre para “datos de escala nominal”. No es nada que no hayamos discutido ya, sólo que en el contexto del análisis de datos, la gente tiende a usar el término “datos categóricos” en lugar de “datos de escala nominal”. No sé por qué. En cualquier caso, análisis de datos categóricos se refiere a una colección de herramientas que puedes usar cuando tus datos son de escala nominal. Sin embargo, hay muchas herramientas diferentes que se pueden usar para el análisis de datos categóricos, y este capítulo cubre solo algunas de las más comunes.

10.1 La prueba de bondad de ajuste $\chi^2$ (ji-cuadrado)

La prueba de bondad de ajuste $\chi^2$ es una de las pruebas de hipótesis más antiguas que existen. Fue inventada por Karl Pearson alrededor del cambio de siglo (Pearson, 1900), con algunas correcciones hechas más tarde por Sir Ronald Fisher (Fisher, 1922). Comprueba si una distribución de frecuencias observadas de una variable nominal coincide con una distribución de frecuencias esperadas. Por ejemplo, supongamos que un grupo de pacientes se sometió a un tratamiento experimental y se les evaluó la salud para ver si su condición mejoró, permaneció igual o empeoró. Se podría usar una prueba de bondad de ajuste para determinar si los números en cada categoría (mejorado, sin cambios, empeorado) coinciden con los números que se esperarían dada la opción de tratamiento estándar. Pensemos en esto un poco más, con algo de psicología.

10.1.1 Los datos de las cartas

A lo largo de los años, se han realizado muchos estudios que muestran que a los humanos les resulta difícil simular la aleatoriedad. Por mucho que intentemos “actuar” al azar, pensamos en términos de patrones y estructura y, por lo tanto, cuando se nos pide que “hagamos algo al azar”, lo que la gente realmente hace es cualquier cosa menos aleatorio. Como consecuencia, el estudio de la aleatoriedad humana (o la no aleatoriedad, según sea el caso) abre muchas preguntas psicológicas profundas sobre cómo pensamos sobre el mundo. Con esto en mente, consideremos un estudio muy simple. Supongamos que le pido a la gente que imagine un mazo de cartas barajado y que elija mentalmente una carta de este mazo imaginario “al azar”. Después de que hayan elegido una carta, les pido que seleccionen mentalmente una segunda. Para ambas opciones, lo que vamos a ver es el palo (corazones, tréboles, picas o diamantes) que eligió la gente. Después de pedir, digamos, $N = 200$ personas que haga esto, me gustaría ver los datos y averiguar si las cartas que las personas pretendían seleccionar eran realmente aleatorias o no. Los datos están contenidos en el archivo randomness.csv en el que, cuando lo abres en jamovi y echas un vistazo a la vista de hoja de cálculo, verás tres variables. Estas son: una variable id que asigna un identificador único a cada participante, y las dos variables elección_1 y elección_2 que indican los palos de cartas que eligieron las personas.

Por el momento, concentrémonos en la primera elección que hizo la gente. Usaremos la opción Tablas de frecuencia en ‘Exploración’ - ‘Descriptivos’ para contar la cantidad de veces que observamos a las personas elegir cada palo. Esto es lo que obtenemos (Table 10.1):

Table 10.1:
Número de veces que se eligió cada palo
clubs	diamonds	hearts	spades
35	51	64	50

Esa pequeña tabla de frecuencias es bastante útil. Al mirarla, hay un indicio de que es más probable que la gente elija corazones que tréboles, pero no es del todo obvio si eso es cierto o si se debe al azar. Así que probablemente tendremos que hacer algún tipo de análisis estadístico para averiguarlo, que es de lo que voy a hablar en la siguiente sección.

Excelente. A partir de este momento, trataremos esta tabla como los datos que buscamos analizar. Sin embargo, dado que voy a tener que hablar sobre estos datos en términos matemáticos (¡lo siento!), podría ser una buena idea aclarar cuál es la notación. En notación matemática, acortamos la palabra legible por humanos “observado” a la letra $O$, y usamos subíndices para indicar la posición de la observación. Entonces, la segunda observación en nuestra tabla se escribe como $O_2$ en matemáticas. La relación entre las descripciones en español y los símbolos matemáticos se ilustra en Table 10.2.

Table 10.2:
Relación entre las descripciones en español y los símbolos matemáticos
label	index, i	math. symbol	the value
clubs, $ \clubsuit $	1	$ O_1 $	35
diamonds, $ \diamondsuit $	2	$ O_2 $	51
hearts, $ \heartsuit $	3	$ O_3 $	64
spades, $ \spadesuit $	4	$ O_4 $	50

Espero que haya quedado claro. También vale la pena señalar que los matemáticos prefieren hablar de cosas generales en lugar de específicas, por lo que también verás la notación $O_i$, que se refiere al número de observaciones que se encuentran dentro de la i-ésima categoría (donde i podría ser 1, 2, 3 o 4). Finalmente, si queremos referirnos al conjunto de todas las frecuencias observadas, los estadísticos agrupan todos los valores observados en un vector ², al que me referiré como $O$.

\[O = (O_1, O_2, O_3, O_4)\]

Una vez más, esto no es nada nuevo o interesante. Es solo notación. Si digo que $O = (35, 51, 64, 50)$ todo lo que estoy haciendo es describir la tabla de frecuencias observadas (es decir, observadas), pero me estoy refiriendo a ella usando notación matemática.

10.1.2 La hipótesis nula y la hipótesis alternativa

Como se indicó en la última sección, nuestra hipótesis de investigación es que “la gente no elige cartas al azar”. Lo que vamos a querer hacer ahora es traducir esto en algunas hipótesis estadísticas y luego construir una prueba estadística de esas hipótesis. La prueba que te voy a describir es la prueba de bondad de ajuste de Pearson $\chi^2$ (ji-cuadrado) y, como ocurre a menudo, tenemos que comenzar construyendo cuidadosamente nuestra hipótesis nula. En este caso, es bastante fácil. Primero, expresemos la hipótesis nula en palabras:

\[H_0: \text{ Los cuatro palos se eligen con la misma probabilidad}\]

Ahora, debido a que esto es estadística, tenemos que poder decir lo mismo de manera matemática. Para hacer esto, usemos la notación $P_j$ para referirnos a la verdadera probabilidad de que se elija el j-ésimo palo. Si la hipótesis nula es verdadera, entonces cada uno de los cuatro palos tiene un 25% de posibilidades de ser seleccionado. En otras palabras, nuestra hipótesis nula afirma que $P_1 = .25$, $P_2 = .25$, $P3 = .25$ y finalmente que $P_4 = .25$. Sin embargo, de la misma manera que podemos agrupar nuestras frecuencias observadas en un vector O que resume todo el conjunto de datos, podemos usar P para referirnos a las probabilidades que corresponden a nuestra hipótesis nula. Entonces, si permito que el vector $P = (P_1, P_2, P_3, P_4)$ se refiera a la colección de probabilidades que describen nuestra hipótesis nula, entonces tenemos:

\[H_0: P =(.25, .25, .25, .25)\]

En este caso particular, nuestra hipótesis nula corresponde a un vector de probabilidades P en el que todas las probabilidades son iguales entre sí. Pero esto no tiene por qué ser así. Por ejemplo, si la tarea experimental fuera que las personas imaginaran que estaban sacando de una baraja que tenía el doble de tréboles que cualquier otro palo, entonces la hipótesis nula correspondería a algo así como $P = (.4, .2, .2 , .2)$. Mientras las probabilidades sean todas positivas y sumen 1, entonces es una opción perfectamente legítima para la hipótesis nula. Sin embargo, el uso más común de la prueba de bondad de ajuste es probar la hipótesis nula de que todas las categorías tienen la misma probabilidad, por lo que nos ceñiremos a eso para nuestro ejemplo.

¿Qué pasa con nuestra hipótesis alternativa, $H_1$? Todo lo que realmente nos interesa es demostrar que las probabilidades involucradas no son todas idénticas (es decir, las elecciones de las personas no fueron completamente aleatorias). En consecuencia, las versiones “humanas” de nuestras hipótesis son las siguientes:

$H_0: \text{ Los cuatro palos se eligen con la misma probabilidad}$ $H_1: \text{ Al menos una de las probabilidades de elección de palo no es 0.25}$

… y la versión “apta para matemáticos” es:

$H_0: P= (.25, .25, .25, .25)$ $H_1: P \neq (.25, .25, .25, .25)$

10.1.3 La prueba estadística de “bondad de ajuste”

En este punto, tenemos nuestras frecuencias observadas O y una colección de probabilidades P correspondientes a la hipótesis nula que queremos probar. Lo que ahora queremos hacer es construir una prueba de la hipótesis nula. Como siempre, si queremos probar $H_0$ contra $H_1$, vamos a necesitar una prueba estadística. El truco básico que utiliza una prueba de bondad de ajuste es construir una prueba estadística que mida cuán “cercanos” están los datos a la hipótesis nula. Si los datos no se parecen a lo que “esperaría” ver si la hipótesis nula fuera cierta, entonces probablemente no sea cierta. Bien, si la hipótesis nula fuera cierta, ¿qué esperaríamos ver? O, para usar la terminología correcta, ¿cuáles son las frecuencias esperadas? Hay $N = 200$ observaciones y (si el valor nulo es verdadero) la probabilidad de que cualquiera de ellas elija un corazón es $P_3 = 0,25$, así que supongo que esperamos $200 x 0,25 = 50$ corazones, ¿verdad? O, más específicamente, si dejamos que Ei se refiera a “el número de respuestas de la categoría i que esperamos si el valor nulo es verdadero”, entonces

\[E_i=N \times P_i\]

Esto es bastante fácil de calcular. Si hay 200 observaciones que pueden clasificarse en cuatro categorías, y pensamos que las cuatro categorías son igualmente probables, entonces, en promedio, esperaríamos ver 50 observaciones en cada categoría, ¿verdad?

Ahora, ¿cómo traducimos esto en una prueba estadística? Claramente, lo que queremos hacer es comparar el número esperado de observaciones en cada categoría ($E_i$) con el número observado de observaciones en esa categoría ($O_i$). Y sobre la base de esta comparación deberíamos poder llegar a una buena prueba estadística. Para empezar, calculemos la diferencia entre lo que la hipótesis nula esperaba que encontráramos y lo que realmente encontramos. Es decir, calculamos la puntuación de diferencia “observada menos esperada”, $O_i - E_i$ . Esto se ilustra en Table 10.3.

Table 10.3:
frecuencias esperadas y observadas
	$ \clubsuit $	$ \diamondsuit $	$ \heartsuit $	$ \spadesuit $
expected frequency $ E_i$	50	50	50	50
observed frequency $ O_i$	35	51	64	50
difference score $ O_i-E_i$	-15	1	14	0

Así, según nuestros cálculos, está claro que la gente eligió más corazones y menos tréboles de lo que predijo la hipótesis nula. Sin embargo, un momento de reflexión sugiere que estas diferencias en bruto no son exactamente lo que estamos buscando. Intuitivamente, parece que es tan malo cuando la hipótesis nula predice muy pocas observaciones (que es lo que sucedió con los corazones) como cuando predice demasiadas (que es lo que sucedió con los tréboles). Entonces es un poco extraño que tengamos un número negativo para los tréboles y un número positivo para los corazones. Una manera fácil de arreglar esto es elevar todo al cuadrado, de modo que ahora calculemos las diferencias al cuadrado, $(E_i - O_i)^2$ . Como antes, podemos hacer esto a mano (Table 10.4).

Table 10.4:
elevar al cuadrado las diferencias en las puntuaciones
$ \clubsuit $	$ \diamondsuit $	$ \heartsuit $	$ \spadesuit $
225	1	196	0

Ahora estamos progresando. Lo que tenemos ahora es una colección de números que son grandes cuando la hipótesis nula hace una mala predicción (tréboles y corazones), pero son pequeños cuando hace una buena (diamantes y picas). A continuación, por algunas razones técnicas que explicaré en un momento, también dividamos todos estos números por la frecuencia esperada Ei, de modo que en realidad estemos calculando $\frac{(E_i-O_i)^2}{E_i}$ . Dado que $E_i = 50$ para todas las categorías en nuestro ejemplo, no es un cálculo muy interesante, pero hagámoslo de todos modos (Table 10.5).

Table 10.5:
dividir las diferencias de puntuaciones al cuadrado por la frecuencia esperada para proporcionar una puntuación de ‘error’
$ \clubsuit $	$ \diamondsuit $	$ \heartsuit $	$ \spadesuit $
4.50	0.02	3.92	0.00

En efecto, lo que tenemos aquí son cuatro puntuaciones de “error” diferentes, cada una de las cuales nos indica la magnitud del “error” que cometió la hipótesis nula cuando intentamos usarla para predecir nuestras frecuencias observadas. Entonces, para convertir esto en una prueba estadística útil, una cosa que podríamos hacer es simplemente sumar estos números. El resultado se denomina estadístico de bondad de ajuste, conocido convencionalmente como $\chi^2$ (ji-cuadrado) o GOF. Podemos calcularlo como en Table 10.6.

\[\sum( (observado - esperado)^2 / esperado)\]

Esto nos da un valor de 8,44.

[Detalle técnico adicional ³]

Como hemos visto en nuestros cálculos, en nuestro conjunto de datos de cartas tenemos un valor de $\chi^2$ = 8,44. Entonces, ahora la pregunta es si este es un valor lo suficientemente grande como para rechazar el la hipótesis nula.

10.1.4 La distribución muestral del estadístico GOF

Para determinar si un valor particular de $\chi^2$ es o no lo suficientemente grande como para justificar el rechazo de la hipótesis nula, necesitaremos averiguar cuál sería la distribución muestral para $\chi^2$ si la hipótesis nula fuera cierta. Así que eso es lo que voy a hacer en esta sección. Te mostraré con bastante detalle cómo se construye esta distribución muestral y luego, en la siguiente sección, la usaré para construir una prueba de hipótesis. Si quieres ir al grano y estás dispuesta a confiar en que la distribución muestral es una distribución $\chi^2$ (ji-cuadrado) con $k - 1$ grados de libertad, puedes omitir el resto de esta sección. Sin embargo, si deseas comprender por qué la prueba de bondad de ajuste funciona de la forma en que lo hace, sigue leyendo.

Bien, supongamos que la hipótesis nula es realmente cierta. Si es así, entonces la verdadera probabilidad de que una observación caiga en la i-ésima categoría es $P_i$. Después de todo, esa es más o menos la definición de nuestra hipótesis nula. Pensemos en lo que esto realmente significa. Esto es como decir que la “naturaleza” toma la decisión sobre si la observación termina o no en la categoría i al lanzar una moneda ponderada (es decir, una donde la probabilidad de obtener cara es $P_j$). Y, por lo tanto, podemos pensar en nuestra frecuencia observada $O_i$ imaginando que la naturaleza lanzó N de estas monedas (una para cada observación en el conjunto de datos), y exactamente $O_i$ de ellas salieron cara. Obviamente, esta es una forma bastante extraña de pensar en el experimento. Pero lo que hace (espero) es recordarte que en realidad hemos visto este escenario antes. Es exactamente la misma configuración que dio lugar a Section 7.4 en Chapter 7. En otras palabras, si la hipótesis nula es verdadera, se deduce que nuestras frecuencias observadas se generaron muestreando a partir de una distribución binomial:

\[O_i \sum Binomial(P_i,N)\]

Ahora bien, si recuerdas nuestra discusión sobre Section 8.3.3, la distribución binomial empieza a parecerse bastante a la distribución normal, especialmente cuando $N$ es grande y cuando $P_i$ no está demasiado cerca a 0 o 1. En otras palabras, siempre que $N^P_i$ sea lo suficientemente grande. O, dicho de otro modo, cuando la frecuencia esperada Ei es lo suficientemente grande, entonces la distribución teórica de $O_i$ es aproximadamente normal. Mejor aún, si $O_i$ se distribuye normalmente, entonces también lo es $(O_i-E_i)/\sqrt{(E_i)}$ . Dado que $E_i$ es un valor fijo, restando Ei y dividiendo por ? Ei cambia la media y la desviación estándar de la distribución normal, pero eso es todo lo que hace. Bien, ahora echemos un vistazo a cuál es realmente nuestro estadístico de bondad de ajuste. Lo que estamos haciendo es tomar un montón de cosas que están normalmente distribuidas, elevarlas al cuadrado y sumarlas. Espera. ¡También lo hemos visto antes! Como discutimos en la sección sobre Section 7.6, cuando tomas un montón de cosas que tienen una distribución normal estándar (es decir, media 0 y desviación estándar 1), las elevas al cuadrado y luego las sumas, la cantidad resultante tiene una distribución ji-cuadrado. Así que ahora sabemos que la hipótesis nula predice que la distribución muestral del estadístico de bondad de ajuste es una distribución de ji-cuadrado. Genial.

Hay un último detalle del que hablar, a saber, los grados de libertad. Si recuerdas Section 7.6, dije que si el número de cosas que está sumando es k, entonces los grados de libertad para la distribución de ji-cuadrado resultante es k. Sin embargo, lo que dije al comienzo de esta sección es que los grados de libertad reales para la prueba de bondad de ajuste de ji-cuadrado son $k - 1$. ¿Por qué? La respuesta aquí es que lo que se supone que estamos mirando es el número de cosas realmente independientes que se suman. Y, como continuaré hablando en la siguiente sección, aunque hay k cosas que estamos agregando solo $k - 1$ de ellas son realmente independientes, por lo que los grados de libertad en realidad son solo $k - 1$. Ese es el tema de la siguiente sección⁴.

10.1.5 Grados de libertad

Figure 10.1: distribuciones $\chi^2$ (ji-cuadrado) con diferentes valores para los ‘grados de libertad’

Cuando introduje la distribución de ji-cuadrado en Section 7.6, fui un poco imprecisa sobre lo que “grados de libertad” significa realmente. Obviamente, es importante. Si observamos Figure 10.1, podemos ver que si cambiamos los grados de libertad, la distribución de ji-cuadrado cambia de forma bastante sustancial. ¿Pero qué es exactamente? Una vez más, cuando presenté la distribución y expliqué su relación con la distribución normal, ofrecí una respuesta: es el número de “variables normalmente distribuidas” que estoy elevando al cuadrado y sumando. Pero, para la mayoría de las personas, eso es algo abstracto y no del todo útil. Lo que realmente necesitamos hacer es tratar de comprender los grados de libertad en términos de nuestros datos. Así que aquí va.

La idea básica detrás de los grados de libertad es bastante sencilla. Se calculan contando el número de “cantidades” distintas que se utilizan para describir los datos y restando todas las “restricciones” que esos datos deben satisfacer.⁵ Esto es un poco vago, así que usemos los datos de nuestras cartas como un ejemplo concreto. Describimos nuestros datos utilizando cuatro números, $O1, O2, O3$ y O4 correspondientes a las frecuencias observadas de las cuatro categorías diferentes (corazones, tréboles, diamantes, picas). Estos cuatro números son los resultados aleatorios de nuestro experimento. Pero mi experimento en realidad tiene una restricción fija incorporada: el tamaño de la muestra $N$. ⁶ Es decir, si sabemos

cuántas personas eligieron corazones, cuántas eligieron diamantes y cuántas eligieron tréboles, entonces podríamos averiguar exactamente cuántas eligieron espadas. En otras palabras, aunque nuestros datos se describen usando cuatro números, en realidad solo corresponden a $4 - 1 = 3$ grados de libertad. Una forma ligeramente diferente de pensar al respecto es notar que hay cuatro probabilidades que nos interesan (nuevamente, correspondientes a las cuatro categorías diferentes), pero estas probabilidades deben sumar uno, lo que impone una restricción. Por lo tanto los grados de libertad son $4 - 1 = 3$. Independientemente de si deseas pensar en términos de frecuencias observadas o en términos de probabilidades, la respuesta es la misma. En general, cuando se ejecuta la prueba de bondad de ajuste $\chi^2$(ji-cuadrado) para un experimento con $k$ grupos, los grados de libertad serán $k - 1$.

10.1.6 Probando la hipótesis nula

El paso final en el proceso de construcción de nuestra prueba de hipótesis es averiguar cuál es la región de rechazo. Es decir, qué valores de $\chi^2$ nos llevarían a rechazar la hipótesis nula. Como vimos anteriormente, los valores grandes de $\chi^2$ implican que la hipótesis nula no ha hecho un buen trabajo al predecir los datos de nuestro experimento, mientras que los valores pequeños de $\chi^2$ implican que en realidad se ha hecho bastante bien. Por lo tanto, una estrategia bastante sensata sería decir que hay algún valor crítico tal que si $\chi^2$ es mayor que el valor crítico, rechazamos el valor nulo, pero si $\chi^2$ es menor que este valor, mantenemos la hipótesis nula. En otras palabras, para usar el lenguaje que introdujimos en Chapter 9, la prueba de bondad de ajuste ji-cuadrado es siempre una prueba unilateral. Correcto, entonces todo lo que tenemos que hacer es averiguar cuál es este valor crítico. Y es bastante sencillo. Si queremos que nuestra prueba tenga un nivel de significación de $\alpha = .05$ (es decir, estamos dispuestas a tolerar una tasa de error Tipo I de $5%$), entonces tenemos que elegir nuestro valor crítico de modo que solo haya una probabilidad del 5% de que $\chi^2$ pueda llegar a ser tan grande si la hipótesis nula es cierta. Esto se ilustra en Figure 10.2.

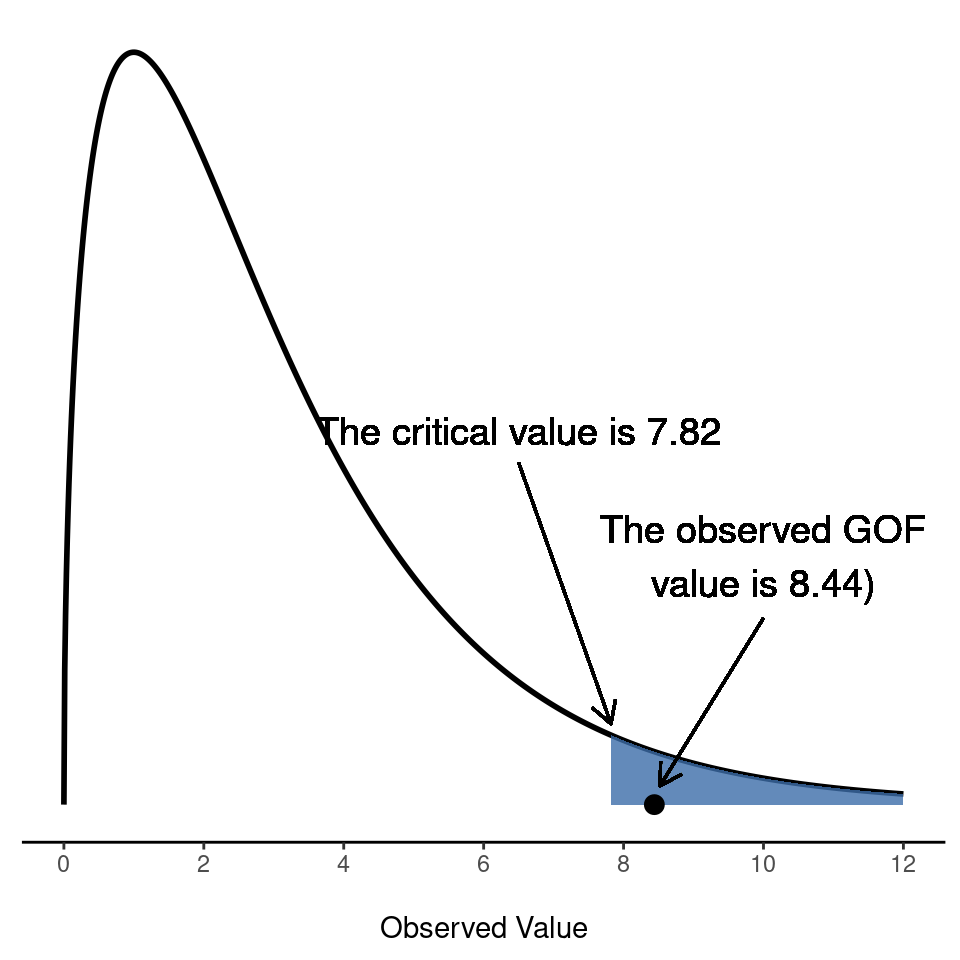
Figure 10.2: Ilustración de cómo funciona la prueba de hipótesis para la prueba de bondad de ajuste $\chi^2$ (ji-cuadrado)

Ah, pero te escucho preguntar, ¿cómo encuentro el valor crítico de una distribución ji-cuadrado con $k-1$ grados de libertad? Hace muchos años, cuando tomé por primera vez una clase de estadística de psicología, solíamos buscar estos valores críticos en un libro de tablas de valores críticos, como el de Figure 10.3. Mirando esta figura, podemos ver que el valor crítico para una distribución $\chi^2$ con 3 grados de libertad y p=0.05 es 7.815.

Figure 10.3: Tabla de valores críticos para la distribución ji-cuadrado

Así, si nuestro estadístico $\chi^2$ calculado es mayor que el valor crítico de $7.815$, entonces podemos rechazar la hipótesis nula (recuerda que la hipótesis nula, $H_0$, es que los cuatro palos se eligen con la misma probabilidad). Como en realidad ya lo calculamos antes (es decir, $\chi^2$ = 8,44), podemos rechazar la hipótesis nula. Y eso es todo, básicamente. Ahora conoces la “prueba de $\chi^2$ de Pearson para la bondad de ajuste”. Qué suerte tienes.

10.1.7 Haciendo la prueba en jamovi

No es sorprendente que jamovi proporcione un análisis que hará estos cálculos por ti. Usemos el archivo Randomness.omv. En la barra de herramientas principal de ‘Análisis’, selecciona ‘Frecuencias’ - ‘Pruebas de proporción de una muestra’ - ‘$N$ Resultados’. Luego, en la ventana de análisis que aparece, mueve la variable que deseas analizar (opción 1) al cuadro ‘Variable’. Además, haz clic en la casilla de verificación ‘Recuentos esperados’ para que se muestren en la tabla de resultados. Cuando hayas terminado todo esto, deberías ver los resultados del análisis en jamovi como en Figure 10.4. No sorprende entonces que jamovi proporcione los mismos recuentos y estadísticos esperados que calculamos a mano anteriormente, con un valor de $\chi^2$ de $ (8.44$ con $3$ gl y $p=0.038$. Ten en cuenta que ya no necesitamos buscar un valor umbral de valor p crítico, ya que jamovi nos da el valor p real del $\chi^ calculado 2$ por $3$

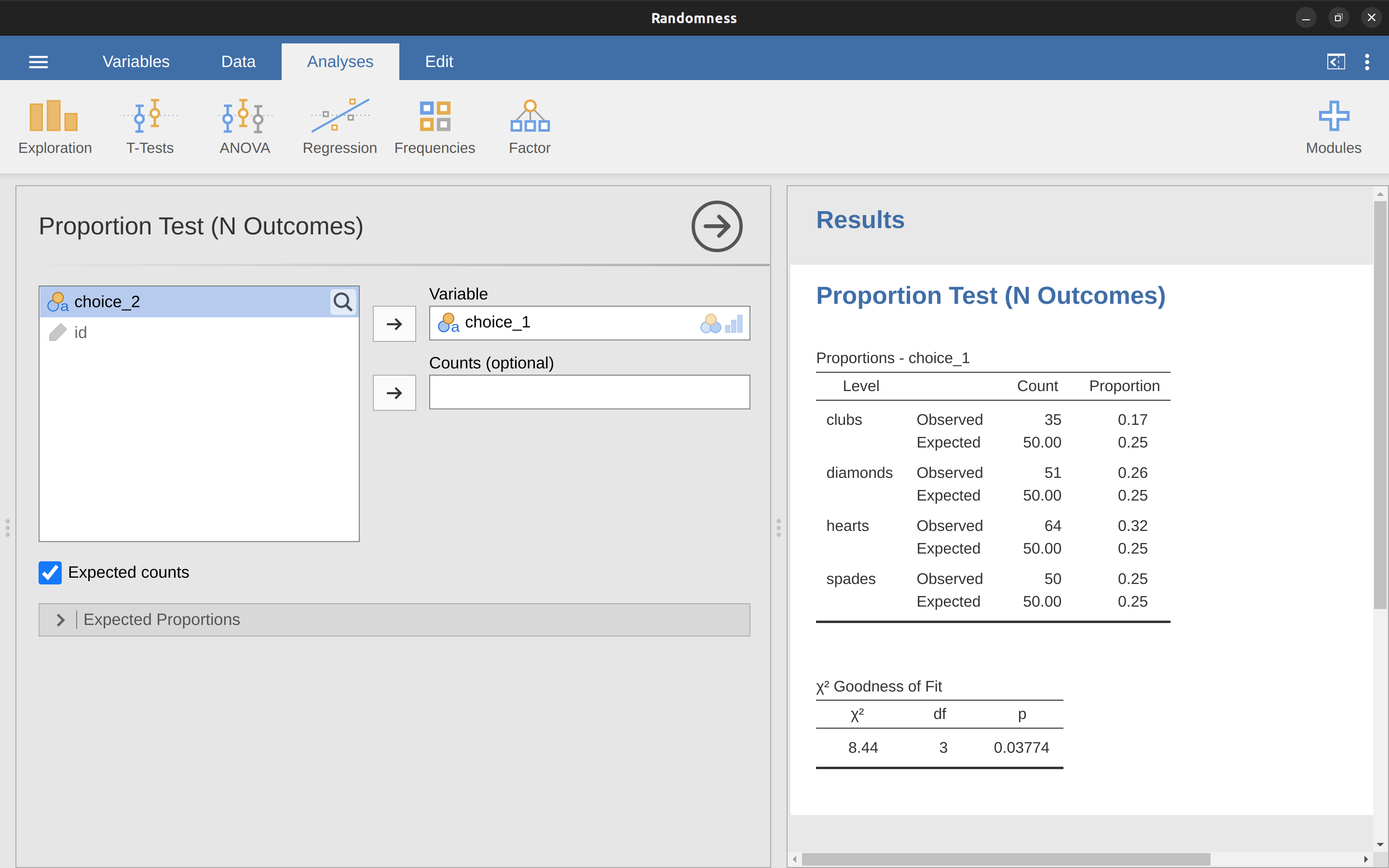
Figure 10.4: Una prueba de proporciones de una muestra de $\chi^2$ en jamovi, con una tabla que muestra las frecuencias y proporciones tanto observadas como esperadas

10.1.8 Especificando una hipótesis nula diferente

En este punto, es posible que te preguntes qué hacer si deseas realizar una prueba de bondad de ajuste, pero tu hipótesis nula no es que todas las categorías sean igualmente probables. Por ejemplo, supongamos que alguien hubiera hecho la predicción teórica de que las personas deberían elegir cartas rojas $60\%$ del tiempo y cartas negras $40\%$ del tiempo (no tengo ni idea de por qué predecirías eso), pero no tenía otras preferencias. Si ese fuera el caso, la hipótesis nula sería esperar que $30\%$ de las opciones fueran corazones, $30\%$ diamantes, $20\%$ picas y $20\%$ tréboles. En otras palabras, esperaríamos que los corazones y los diamantes aparecieran 1,5 veces más que las picas y los tréboles (la proporción $30\%$ : $20\%$ es lo mismo que 1,5 : 1). Esto me parece una teoría tonta, y es bastante fácil probar esta hipótesis nula explícitamente especificada con los datos de nuestro análisis jamovi. En la ventana de análisis (etiquetada como ‘Prueba de proporción (N resultados)’ en Figure 10.4, puedes expandir las opciones para ‘Proporciones esperadas’. Si haces esto, hay opciones para introducir diferentes valores de relación para la variable que has seleccionado, en nuestro caso esta es la opción 1. Cambia la relación para reflejar la nueva hipótesis nula, como en Figure 10.5, y fíjate cómo cambian los resultados.

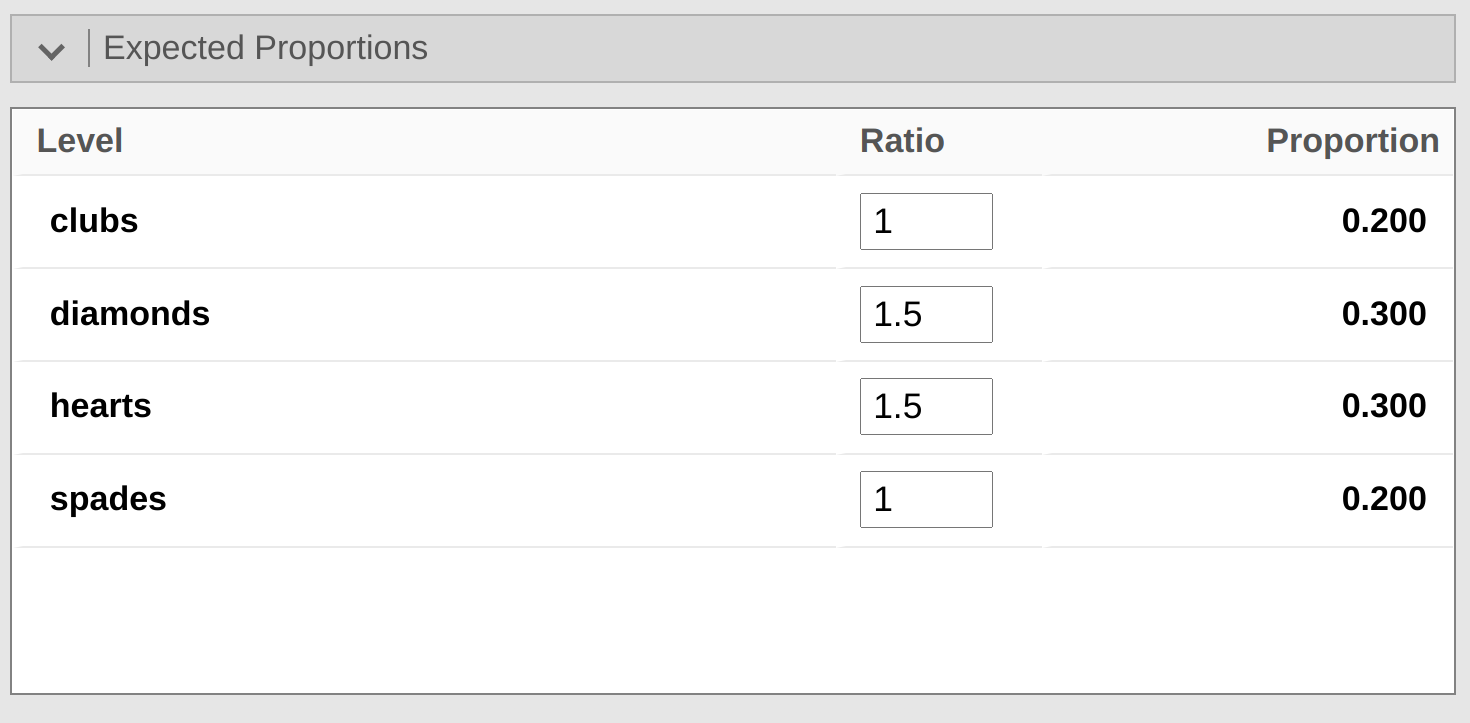
Figure 10.5: cambiar las proporciones esperadas en la prueba de proporciones de una muestra de $\\chi^2$ en jamovi

Los recuentos esperados ahora se muestran en Table 10.6.

Table 10.6:
recuentos esperados para una hipótesis nula diferente
	$ \clubsuit $	$ \diamondsuit $	$ \heartsuit $	$ \spadesuit $
expected frequency $ E_i$	40	60	60	40

y el estadístico $\chi^2$ es 4,74, 3 gl, $p = 0,182$. Ahora, los resultados de nuestras hipótesis actualizadas y las frecuencias esperadas son diferentes a las de la última vez. Como consecuencia, nuestra prueba estadística $\chi^2$ es diferente, y nuestro valor p también es diferente. Desgraciadamente, el valor p es $ 0,182 $, por lo que no podemos rechazar la hipótesis nula (consulta Section 9.5 para recordar por qué). Lamentablemente, a pesar de que la hipótesis nula corresponde a una teoría muy tonta, estos datos no aportan pruebas suficientes en su contra.

10.1.9 Cómo informar los resultados de la prueba

Así que ahora sabes cómo funciona la prueba y sabes cómo hacer la prueba usando una maravillosa caja de informática mágica con sabor a jamovi. Lo siguiente que necesitas saber es cómo escribir los resultados. Después de todo, no tiene sentido diseñar y ejecutar un experimento y luego analizar los datos si no se lo cuentas a nadie. Así que ahora hablemos de lo que debes hacer al informar tu análisis. Sigamos con nuestro ejemplo de palos de cartas. Si quisieras escribir este resultado para un artículo o algo así, entonces la forma convencional de informar esto sería escribir algo como esto:

De los 200 participantes en el experimento, 64 seleccionaron corazones para su primera opción, 51 seleccionaron diamantes, 50 seleccionaron picas y 35 seleccionaron tréboles. Se realizó una prueba de bondad de ajuste de ji-cuadrado para comprobar si las probabilidades de elección eran idénticas para los cuatro palos. Los resultados fueron significativos ($\chi^2(3) = 8.44, p< .05)$, lo que sugiere que las personas no eligieron cartas puramente al azar.

Esto es bastante sencillo y, es de esperar que parezca bastante anodino. Dicho esto, hay algunas cosas que debes tener en cuenta sobre esta descripción:

La prueba estadística va precedida por la estadística descriptiva. Es decir, le he dicho al lector algo sobre el aspecto de los datos antes de pasar a hacer la prueba. En general, esta es una buena práctica. Recuerda siempre que tu lector no conoce tus datos tan bien como tú. Así que, a menos que se los describas correctamente, las pruebas estadísticas no tendrán ningún sentido para ellos y se sentirán frustrados y llorarán.
La descripción te dice cuál es la hipótesis nula que se está probando. A decir verdad, los escritores no siempre lo hacen, pero suele ser una buena idea en situaciones de ambigüedad, o cuando no se puede confiar en que los lectores conozcan a fondo las herramientas estadísticas que se utilizan. Muy a menudo, es posible que el lector no sepa (o recuerde) todos los detalles de la prueba que estás utilizando, ¡así que es una especie de cortesía “recordárselos”! En lo que respecta a la prueba de bondad de ajuste, generalmente puedes confiar en que una audiencia científica sepa cómo funciona (ya que se trata en la mayoría de las clases de introducción a la estadística). Sin embargo, sigue siendo una buena idea ser explícito al establecer la hipótesis nula (¡brevemente!) porque la hipótesis nula puede ser diferente dependiendo de para qué estés usando la prueba. Por ejemplo, en el ejemplo de las cartas, mi hipótesis nula era que las probabilidades de los cuatro palos eran idénticas (es decir, $P1 = P2 = P3 = P4 = 0,25$), pero esa hipótesis no tiene nada de especial. Podría haber probado fácilmente la hipótesis nula de que $P_1 = 0.7$ y $P2 = P3 = P4 = 0.1$ usando una prueba de bondad de ajuste. Por lo tanto, es útil para el lector que le expliques cuál era tu hipótesis nula. Además, fíjate que describí la hipótesis nula en palabras, no en matemáticas. Eso es perfectamente aceptable. Puedes describirlo en matemáticas si lo deseas, pero dado que la mayoría de los lectores encuentran que las palabras son más fáciles de leer que los símbolos, la mayoría de los escritores tienden a describir la hipótesis nula usando palabras si pueden.
Se incluye un “bloque de estadísticos”. Cuando informé los resultados de la prueba en sí, no solo dije que el resultado era significativo, incluí un “bloque de estadísticos” (es decir, la parte densa de aspecto matemático entre paréntesis) que aporta toda la información estadística “clave”. Para la prueba de bondad de ajuste ji-cuadrado, la información que se informa es la prueba estadística (que el estadístico de bondad de ajuste fue 8.44), la información sobre la distribución utilizada en la prueba ($\chi^2$ con 3 grados de libertad que normalmente se abrevia a $\chi^2$(3)), y luego la información sobre si el resultado fue significativo (en este caso $p< .05$). La información particular que debe incluirse en el bloque de estadísticos es diferente para cada prueba, por lo que cada vez que presente una nueva prueba, te mostraré cómo debería ser el bloque de estadísticos.⁷ Sin embargo, el principio general es que siempre debes proporcionar suficiente información para que el lector pueda verificar los resultados de la prueba por sí mismo si realmente lo desea.
Los resultados son interpretados. Además de indicar que el resultado era significativo, proporcioné una interpretación del resultado (es decir, que la gente no eligió al azar). Esto también es una gentileza para el lector, porque le dice algo sobre lo que debe creer acerca de lo que está pasando en sus datos. Si no incluyes algo como esto, es muy difícil para tu lector entender lo que está pasando.⁸

Como con todo lo demás, tu principal preocupación debe ser explicar las cosas a tu lector. Recuerda siempre que el objetivo de informar tus resultados es comunicarlo a otro ser humano. No puedo decirte cuántas veces he visto la sección de resultados de un informe o una tesis o incluso un artículo científico que es simplemente un galimatías, porque el escritor se ha centrado únicamente en asegurarse de haber incluido todos los números y se olvidó de realmente comunicarse con el lector humano.

Satanás se deleita por igual en las estadísticas y en citar las escrituras⁹ – HG pozos

10.2 La prueba de independencia (o asociación) $\chi^2$

GUARDBOT 1: ¡Alto!
GUARDBOT 2: ¿Eres robot o humano?
LEELA: Robot… seremos.
FRY: ¡Ah, sí! ¡Solo dos robots robóticos! ¿eh?
GUARDBOT 1: Administrar la prueba.
GUARDBOT 2: ¿Cuál de las siguientes opciones preferirías? ¿A: Un cachorro, B: Una linda flor de tu amorcito, o C: Un gran archivo de datos con el formato adecuado?
GUARDBOT 1: ¡Elige!
Futurama, “Miedo a un planeta bot”

El otro día estaba viendo un documental animado que examinaba las pintorescas costumbres de los nativos del planeta Chapek 9. Al parecer, para acceder a su capital, el visitante debe demostrar que es un robot y no un ser humano. Para determinar si un visitante es humano o no, los nativos le preguntan si prefiere cachorros, flores o archivos de datos grandes y bien formateados. “Muy ingenioso”, pensé, “pero, ¿y si los humanos y los robots tienen las mismas preferencias? Entonces probablemente no sería una prueba muy buena, ¿verdad?” Resulta que tengo en mis manos los datos de las prueba que las autoridades civiles de Chapek 9 utilizaron para comprobarlo. Lo que hicieron fue muy sencillo. Encontraron un grupo de robots y un grupo de humanos y les preguntaron qué preferían. Guardé sus datos en un archivo llamado chapek9.omv, que ahora podemos cargar en jamovi. Además de la variable ID que identifica a cada persona, hay dos variables de texto nominales, especie y elección. En total, hay 180 entradas en el conjunto de datos, una para cada persona (contando tanto a los robots como a los humanos como “personas”) a quienes se les pidió que hicieran una elección. En concreto, hay 93 humanos y 87 robots, y la opción preferida por abrumadora mayoría es el archivo de datos. Puedes comprobarlo tú misma pidiéndole a jamovi las tablas de frecuencia, en el botón ‘Exploración’ - ‘Descriptivos’. Sin embargo, este resumen no aborda la pregunta que nos interesa. Para hacerlo, necesitamos una descripción más detallada de los datos. Lo que queremos es ver las opciones desglosadas por especies. Es decir, necesitamos tabular los datos de forma cruzada (ver Section 6.1). En jamovi, hacemos esto usando el análisis ‘Frecuencias’ - ‘Tablas de contingencia’ - ‘Muestras independientes’, y deberíamos obtener una tabla parecida a Table 10.7.

Table 10.7:
tabulación cruzada de los datos
	Robot	Human	Total
Puppy	13	15	28
Flower	30	13	43
Data	44	65	109
Total	87	93	180

De ello se desprende claramente que la gran mayoría de los humanos eligieron el archivo de datos, mientras que los robots tendieron a ser mucho más equilibrados en sus preferencias. Dejando a un lado por el momento la pregunta de por qué los humanos son más propensos a elegir el archivo de datos (lo cual parece bastante extraño, hay que reconocerlo), lo primero que tenemos que hacer es determinar si la discrepancia entre las elecciones de los humanos y las de los robots en el conjunto de datos es estadísticamente significativa.

10.2.1 Construyendo nuestra prueba de hipótesis

¿Cómo analizamos estos datos? En concreto, dado que mi hipótesis de investigación es que “los humanos y los robots responden a la pregunta de forma diferente”, ¿cómo puedo construir una prueba de la hipótesis nula de que “los humanos y los robots responden a la pregunta de la misma manera”? Como antes, comenzamos estableciendo una notación para describir los datos (Table 10.8).

Table 10.8:
Notación para describir los datos
	Robot	Human	Total
Puppy	$O_{11}$	$O_{12}$	$R_{1}$
Flower	$O_{21}$	$O_{22}$	$R_{2}$
Data	$O_{31}$	$O_{32}$	$R_{3}$
Total	$C_{1}$	$C_{2}$	N

En esta notación decimos que $O_{ij}$ es un recuento (frecuencia observada) del número de encuestados que son de la especie j (robots o humanos) que dieron la respuesta i (cachorro, flor o datos) cuando se les pidió que hicieran una elección. El número total de observaciones se escribe $N$, como de costumbre. Finalmente, he usado $R_i$ para indicar los totales de las filas (p. ej., $R_1$ es el número total de personas que eligieron la flor) y $C_j$ para indicar los totales de las columnas (p. ej., $C_1$ es el total número de robots).¹⁰

Pensemos ahora en lo que dice la hipótesis nula. Si los robots y los humanos responden de la misma manera a la pregunta, significa que la probabilidad de que “un robot diga cachorro” es la misma que la probabilidad de que “un humano diga cachorro”, y así sucesivamente para las otras dos posibilidades. Entonces, si usamos $P_{ij}$ para denotar “la probabilidad de que un miembro de la especie j dé una respuesta i”, entonces nuestra hipótesis nula es que:

\[ \begin{aligned} H_0 &: \text{Todo lo siguiente es verdadero:} \\ &P_{11} = P_{12}\text{ (misma probabilidad de decir “cachorro”),} \\ &P_{21} = P_{22}\text{ (misma probabilidad de decir “flor”), y} \\ &P_{31} = P_{32}\text{ (misma probabilidad de decir “datos”).} \end{aligned} \]

Y en realidad, dado que la hipótesis nula afirma que las probabilidades verdaderas de elección no dependen de la especie de la persona que hace la elección, podemos dejar que Pi se refiera a esta probabilidad, por ejemplo, P1 es la probabilidad verdadera de elegir al cachorro.

A continuación, de la misma manera que hicimos con la prueba de bondad de ajuste, lo que debemos hacer es calcular las frecuencias esperadas. Es decir, para cada uno de los recuentos observados $O_{ij}$ , necesitamos averiguar qué nos diría la hipótesis nula que debemos esperar. Vamos a denotar esta frecuencia esperada por $E_{ij}$. Esta vez, es un poco más complicado. Si hay un total de $C_j$ personas que pertenecen a la especie $j$, y la verdadera probabilidad de que cualquiera (independientemente de la especie) elija la opción $i$ es $P_i$ , entonces la frecuencia esperada es simplemente:

\[E_{ij}=C_j \times P_i\]

Ahora bien, todo esto está muy bien, pero tenemos un problema. A diferencia de la situación que tuvimos con la prueba de bondad de ajuste, la hipótesis nula en realidad no especifica un valor particular para Pi.

Es algo que tenemos que estimar (ver Chapter 8) a partir de los datos. Afortunadamente, es bastante fácil. Si 28 de 180 personas seleccionaron las flores, una estimación natural de la probabilidad de elegir flores es $\frac{28}{180}$, que es aproximadamente $.16$. Si expresamos esto en términos matemáticos, lo que estamos diciendo es que nuestra estimación de la probabilidad de elegir la opción i es solo el total de la fila dividido por el tamaño total de la muestra:

\[\hat{P}_{i}= \frac{R_i}{N}\]

Por lo tanto, nuestra frecuencia esperada se puede escribir como el producto (es decir, la multiplicación) del total de filas y el total de columnas, dividido por el número total de observaciones:¹¹

\[\hat{E}_{ij}= \frac{R_i \times C_j}{N}\]

[Detalle técnico adicional ¹²]

Como antes, los valores grandes de $X^2$ indican que la hipótesis nula proporciona una mala descripción de los datos, mientras que los valores pequeños de $X^2$ sugieren que hace un buen trabajo al explicar los datos. Por lo tanto, al igual que la última vez, queremos rechazar la hipótesis nula si $X^2$ es demasiado grande.

No es sorprendente que este estadístico tenga una distribución $\chi^2$. Todo lo que tenemos que hacer es averiguar cuántos grados de libertad hay, lo que en realidad no es demasiado difícil. Como mencioné antes, se puede pensar (normalmente) que los grados de libertad son iguales al número de puntos de datos que estás analizando, menos el número de restricciones. Una tabla de contingencia con r filas y c columnas contiene un total de $r^{c}$ frecuencias observadas, por lo que ese es el número total de observaciones. ¿Qué pasa con las restricciones? Aquí, es un poco más complicado. La respuesta es siempre la misma

\[df=(r-1)(c-1)\]

pero la explicación de por qué los grados de libertad toman este valor es diferente dependiendo del diseño experimental. Por ejemplo, supongamos que hubiéramos querido encuestar exactamente a 87 robots y 93 humanos (totales de las columnas fijados por el experimentador), pero hubiéramos dejado que los totales de fila variaran libremente (los totales de fila son variables aleatorias). Pensemos en las restricciones que se aplican en este caso. Bien, puesto que hemos fijado deliberadamente los totales de las columnas por Acto del Experimentador, tenemos restricciones de $c$ allí mismo. Pero, en realidad hay más que eso. ¿Recuerdas que nuestra hipótesis nula tenía algunos parámetros libres (es decir, tuvimos que estimar los valores de Pi)? Esos también importan. No voy a explicar por qué en este libro, pero cada parámetro libre en la hipótesis nula es como una restricción adicional. Entonces, ¿cuántas hay? Bueno, dado que estas probabilidades tienen que sumar 1, solo hay $r - 1$ de estas. Así que nuestros grados de libertad totales son:

\[ \begin{split} df & = \text{(número de observaciones) - (número de restricciones)} \\\\ & = (r \times c) - (c + (r - 1)) \\\\ & = rc - c - r + 1 \\\\ & = (r - 1)(c - 1) \end{split}\]

Por otra parte, supongamos que lo único que el experimentador fijó fue el tamaño total de la muestra N. Es decir, quer interrogamos a las primeras 180 personas que vimos y resultó que 87 eran robots y 93 eran humanos. Esta vez, nuestro razonamiento sería ligeramente diferente, pero nos llevaría a la misma respuesta. Nuestra hipótesis nula sigue siendo $r - 1$ parámetros libres correspondientes a las probabilidades de elección, pero ahora también tiene $c - 1$ parámetros libres correspondientes a las probabilidades de especie, porque también tendríamos que estimar la probabilidad de que una persona muestreada al azar resulte ser un robot.¹³ Finalmente, dado que en realidad fijamos el número total de observaciones N, esa es una restricción más. Por lo tanto, ahora tenemos rc observaciones y $(c-1)+(r-1)+1$ restricciones. ¿Cuál es el resultado?

\[\begin{split} df & = \text{(número de observaciones) - (número de restricciones)} \\\\ & = (r \times c) - ((c-1) + (r - 1)+1) \\\\ & = (r - 1)(c - 1) \end{split} \] Increíble.

10.2.2 Haciendo la prueba en jamovi

Bien, ahora que sabemos cómo funciona la prueba, veamos cómo se hace en jamovi. Por muy tentador que sea guiarte a través de los tediosos cálculos para que te veas obligada a aprenderlo por el camino largo, creo que no tiene sentido. Ya te mostré cómo hacerlo de la manera larga para la prueba de bondad de ajuste en la última sección, y como la prueba de independencia no es conceptualmente diferente, no aprenderás nada nuevo haciéndola de la manera larga. Así que en su lugar voy a ir directamente a mostrarte la manera más fácil. Después de ejecutar la prueba en jamovi (‘Frecuencias’ - ‘Tablas de contingencia’ - ‘Muestras independientes’), todo lo que tienes que hacer es mirar debajo de la tabla de contingencia en la ventana de resultados de jamovi y allí está el estadístico $\chi^2$ para ti. Muestra un valor estadístico $\chi^2$ de 10,72, con 2 gl y valor p = 0,005.

Ha sido fácil, ¿verdad? También puedes pedirle a jamovi que te muestre los recuentos esperados: sólo tienes que hacer clic en la casilla de verificación ‘Recuentos’ - ‘Esperados’ en las opciones de ‘Celdas’ y los recuentos esperados aparecerán en la tabla de contingencia. Y mientras lo haces, sería útil disponer de una medida del tamaño del efecto. Elegiremos la $V$ de Cramer, y puedes especificarlo desde una casilla de verificación en las opciones de ‘Estadísticas’, y da un valor para la $V$ de Cramer de $0,24$. Ver Figure 10.6. Hablaremos de esto más adelante.

Figure 10.6: Prueba de $\chi^2$ de muestras independientes en jamovi usando los datos de Chapek 9

Esta salida nos da suficiente información para escribir el resultado:

El $\chi^2$ de Pearson reveló una asociación significativa entre especie y elección ($\chi^2(2) = 10.7, p< .01)$. Los robots parecían más propensos a decir que prefieren las flores, pero los humanos eran más propensos a decir que preferían los datos.

Fíjate en que, una vez más, he dado un poco de interpretación para ayudar al lector humano a entender qué está pasando con los datos. Más adelante, en mi sección de discusión, proporcionaría un poco más de contexto. Para ilustrar la diferencia, esto es lo que probablemente diría más adelante:

El hecho de que los humanos parezcan preferir más los archivos de datos en bruto que los robots es algo contraintuitivo. Sin embargo, en su contexto tiene cierto sentido, ya que la autoridad civil de Chapek 9 tiene una desafortunada tendencia a matar y diseccionar a los humanos cuando son identificados. Por lo tanto, lo más probable es que los participantes humanos no respondieran honestamente a la pregunta, para evitar consecuencias potencialmente indeseables. Esto debería considerarse una debilidad metodológica importante.

Esto podría clasificarse como un ejemplo bastante extremo de un efecto de reactividad, supongo. Obviamente, en este caso el problema es lo suficientemente grave como para que el estudio sea más o menos inútil como herramienta para comprender las diferencias de preferencias entre humanos y robots. Sin embargo, espero que esto ilustre la diferencia entre obtener un resultado estadísticamente significativo (nuestra hipótesis nula se rechaza a favor de la alternativa) y encontrar algo de valor científico (los datos no nos dicen nada de interés sobre nuestra hipótesis de investigación debido a un gran problema metodológico).

10.3 La corrección de continuidad

Bien, es hora de una pequeña digresión. Te he estado mintiendo un poco hasta ahora. Hay un pequeño cambio que necesitas hacer en los cálculos cuando sólo tengas 1 grado de libertad. Se llama “corrección de continuidad” o, a veces, corrección de Yates. Recuerda lo que señalé antes: la prueba $\chi^2$ se basa en una aproximación, concretamente en el supuesto de que la distribución binomial empieza a parecerse a una distribución normal para $N$ grandes. Uno de los problemas de esto es que a menudo no funciona del todo bien, especialmente cuando solo se tiene 1 grado de libertad (por ejemplo, cuando se realiza una prueba de independencia en una tabla de contingencia de $2 \times 2$). La razón principal principal es que la verdadera distribución muestral para el estadístico $X^{2}$ es en realidad discreta (¡porque se trata de datos categóricos!) pero la distribución $\chi^2$ es continua. Esto puede introducir problemas sistemáticos. En concreto, cuando N es pequeño y cuando $df = 1$, el estadístico de bondad de ajuste tiende a ser “demasiado grande”, lo que significa que en realidad tiene un valor α mayor de lo que piensas (o, de manera equivalente, los valores p son un poco demasiado pequeño).

Por lo que he podido leer en el artículo de Yates¹⁴, la corrección es básicamente un truco. No se deriva de ninguna teoría basada en principios. Más bien, se basa en un examen del comportamiento de la prueba y en la observación de que la versión corregida parece funcionar mejor. Puedes especificar esta corrección en jamovi desde una casilla de verificación en las opciones de ‘Estadísticas’, donde se llama ‘corrección de continuidad $\chi^2$’.

10.4 Tamaño del efecto

Como ya hemos comentado en Section 9.8, cada vez es más habitual pedir a los investigadores que informen sobre alguna medida del tamaño del efecto. Supongamos que hemos realizado la prueba de ji-cuadrado, que resulta ser significativa. Ahora sabes que existe alguna asociación entre las variables (prueba de independencia) o alguna desviación de las probabilidades especificadas (prueba de bondad de ajuste). Ahora deseas informar una medida del tamaño del efecto. Es decir, dado que hay una asociación o desviación, ¿cuán fuerte es?

Hay varias medidas diferentes que puedes elegir para informar y varias herramientas diferentes que puedes usar para calcularlas. No voy a hablar de todas ellas, sino que me centraré en las medidas del tamaño del efecto que se informan con más frecuencia.

Por defecto, las dos medidas que la gente tiende a informar con más frecuencia son el estadístico $\phi$ y la versión algo superior, conocida como $V$ de Cramer.

[Detalle técnico adicional ¹⁵]

Y ya está. Esta parece ser una medida bastante popular, presumiblemente porque es fácil de calcular y da respuestas que no son completamente tontas. Con $V$ de Cramer, se sabe que el valor realmente oscila entre 0 (ninguna asociación) a 1 (asociación perfecta).

10.5 Supuestos de la(s) prueba(s)

Todas las pruebas estadísticas se basan en supuestos y suele ser una buena idea comprobar que se cumplen. En el caso de las pruebas de ji-cuadrado analizadas hasta ahora en este capítulo, los supuestos son:

Las frecuencias esperadas son suficientemente grandes. ¿Recuerdas que en la sección anterior vimos que la distribución muestral $\chi^2$ surge porque la distribución binomial es bastante parecida a una distribución normal? Pues bien, como comentamos en Chapter 7, esto solo es cierto cuando el número de observaciones es suficientemente grande. En la práctica, esto significa es que todas las frecuencias esperadas deben ser razonablemente grandes. ¿Cómo de razonablemente grandes? Las opiniones difieren, pero el supuesto por defecto parece ser que, en general, te gustaría ver todas las frecuencias esperadas mayores de 5, aunque para tablas más grandes, probablemente estaría bien si al menos el 80% de las frecuencias esperadas están por encima de 5 y ninguna está por debajo de 1. Sin embargo, por lo que he podido descubrir (p. ej., Cochran (1954)), estos parecen haber sido propuestos como pautas generales, no reglas estrictas y rápidas, y parecen ser algo conservadoras (Larntz, 1978) .
Los datos son independientes entre sí. Un supuesto algo oculto de la prueba de ji-cuadrado es que tienes que creer de verdad que las observaciones son independientes. Esto es lo que quiero decir. Supongamos que estoy interesada en la proporción de bebés nacidos en un hospital en particular que son niños. Me paseo por las salas de maternidad y observo a 20 niñas y solo 10 niños. Parece una diferencia bastante convincente, ¿verdad? Pero más tarde, resulta que en realidad había entrado en la misma sala 10 veces y, en realidad, solo había visto a 2 niñas y 1 niño. No es tan convincente, ¿verdad? Mis 30 observaciones originales no eran en absoluto independientes y, de hecho, solo equivalían a 3 observaciones independientes. Obviamente, este es un ejemplo extremo (y muy tonto), pero ilustra la cuestión básica. La no independencia “estropea las cosas”. A veces, hace que rechace falsamente la hipótesis nula, como ilustra el ejemplo tonto del hospital, pero también puede ocurrir al contrario. Para dar un ejemplo un poco menos estúpido, consideremos lo que pasaría si hubiera hecho el experimento con las cartas de forma ligeramente diferente. En lugar de pedir a 200 personas que imaginen la selección de una carta al azar, supongamos que pido a 50 personas que seleccionen 4 cartas. Una posibilidad sería que todos seleccionen un corazón, un trébol, un diamante y una pica (de acuerdo con la “heurística de la representatividad” (Tversky & Kahneman, 1974). Se trata de un comportamiento muy poco aleatorio de las personas, pero en este caso obtendría una frecuencia observada de 50 para los cuatro palos. Para este ejemplo, el hecho de que las observaciones no sean independientes (porque las cuatro cartas que elija estarán relacionadas entre sí) en realidad conduce al efecto opuesto, manteniendo falsamente la hipótesis nula.

Si te encuentras en una situación en la que se viola la independencia, puedes utilizar la prueba de McNemar (de la que hablaremos) o la prueba de Cochran (de la que no hablaremos). Del mismo modo, si los recuentos esperados son demasiado pequeños, consulta la prueba exacta de Fisher. A continuación abordaremos estos temas.

10.6 La prueba exacta de Fisher

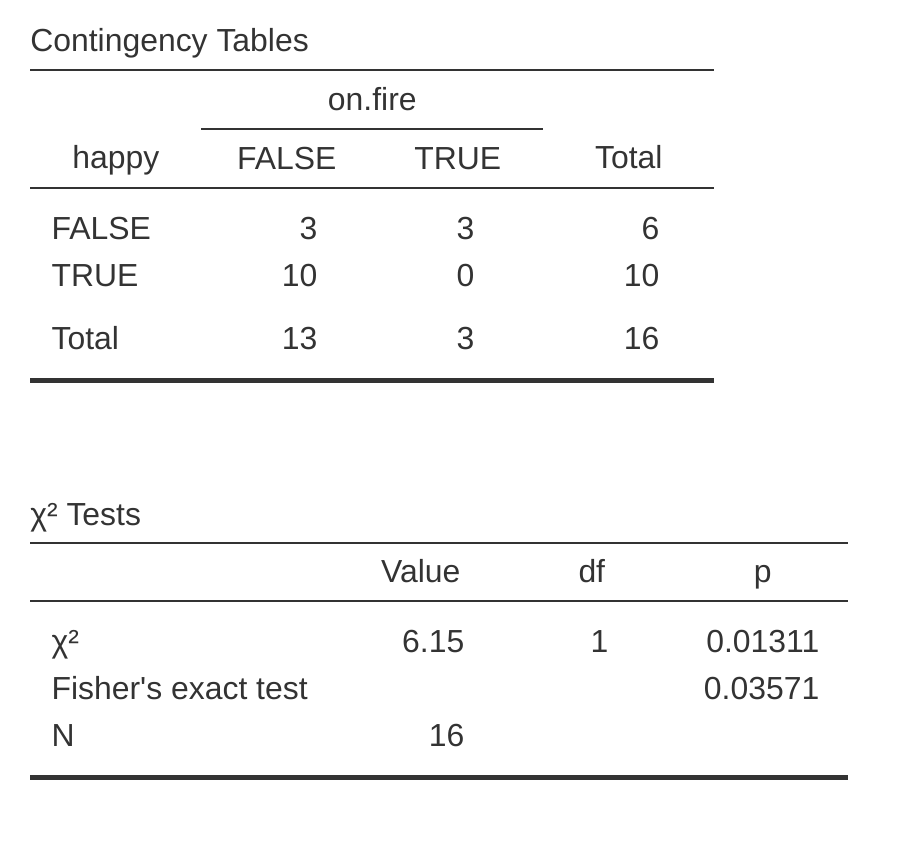
¿Qué hacer si los recuentos en las celdas son demasiado pequeños, pero aún así quieres probar la hipótesis nula de que las dos variables son independientes? Una respuesta sería “recopilar más datos”, pero eso es demasiado simplista. Hay muchas situaciones en las que sería inviable o poco ético hacerlo. Si es así, los estadísticos tienen una especie de obligación moral de proporcionar a los científicos mejores pruebas. En este caso, Fisher (1922) proporcionó amablemente la respuesta correcta a la pregunta. Para ilustrar la idea básica, supongamos que estamos analizando los datos de un experimento de campo que analiza el estado emocional de las personas que han sido acusadas de brujería, algunas de las cuales están siendo quemadas en la hoguera.¹⁶ Desafortunadamente para el científico (pero afortunadamente para la población en general), en realidad es bastante difícil encontrar personas en el proceso de ser prendidas fuego, por lo que los recuentos son terriblemente pequeños en algunos casos. Una tabla de contingencia de los datos de salem.csv ilustra el punto (Table 10.9).

Table 10.9:
tabla de contingencia de los datos de salem.csv
	happy	FALSE	TRUE
on.fire	FALSE	3	10
	TRUE	3	0

Observando estos datos, sería difícil no sospechar que las personas que no están en llamas tienen más probabilidades de ser felices que las que están en llamas. Sin embargo, la prueba de ji-cuadrado hace que esto sea muy difícil de comprobar debido al pequeño tamaño de la muestra. Así que, hablando como alguien que no quiere que le prendan fuego, realmente me gustaría poder obtener una respuesta mejor que esta. Aquí es donde la prueba exacta de Fisher (Fisher, 1922) es muy útil.

La prueba exacta de Fisher funciona de forma algo diferente a la prueba de ji-cuadrado (o, de hecho, a cualquiera de las otras pruebas de hipótesis de las que hablo en este libro) en la medida en que no tiene una prueba estadística, pero calcula el valor p “directamente”. Explicaré los fundamentos de cómo funciona la prueba para una tabla de contingencia de $2 \times 2$. Como antes, vamos a tener un poco de notación (Table 10.10).

Table 10.10:
Notación para la prueba exacta de Fisher
	Happy	Sad	Total
Set on fire	$O_{11}$	$O_{12}$	$R_{1}$
Not set on fire	$O_{21}$	$O_{22}$	$R_{2}$
Total	$C_{1}$	$C_{2}$	$N$

Para construir la prueba, Fisher trata los totales de fila y columna $(R_1, R_2, C_1 \text{ y } C_2)$ como cantidades fijas conocidas y luego calcula la probabilidad de que hubiéramos obtenido las frecuencias observadas que obtuvimos $(O_{11}, O_{12}, O_{21} \text{ and } O_{22})$ dados esos totales. En la notación que desarrollamos en Chapter 7 esto se escribe:

\[P(O_{11}, O_{12}, O_{21}, O_{22} \text{ | } R_1, R_2, C_1, C_2)\] y, como puedes imaginar, es un ejercicio un poco complicado averiguar cuál es esta probabilidad. Pero resulta que esta probabilidad viene descrita por una distribución conocida como distribución hipergeométrica. Lo que tenemos que hacer para calcular nuestro valor p es calcular la probabilidad de observar esta tabla en particular o una tabla “más extrema”. ¹⁷ En la década de 1920, calcular esta suma era desalentador incluso en las situaciones más simples, pero hoy en día es bastante fácil siempre que las tablas no sean demasiado grandes y el tamaño de la muestra no sea demasiado grande. La cuestión conceptualmente complicada es averiguar qué significa decir que una tabla de contingencia es más “extrema” que otra. La solución más sencilla es decir que la tabla con la probabilidad más baja es la más extrema. Esto nos da el valor p.

Puedes especificar esta prueba en jamovi desde una casilla de verificación en las opciones de ‘Estadísticas’ del análisis de ‘Tablas de contingencia’. Cuando se hace esto con los datos del archivo salem.csv, el estadístico de la prueba exacta de Fisher se muestra en los resultados. Lo que más nos interesa aquí es el valor p, que en este caso es lo suficientemente pequeño (p = 0,036) para justificar el rechazo de la hipótesis nula de que las personas que se queman son tan felices como las que no. Ver Figure 10.7.

Figure 10.7: análisis de prueba exacta de Fisher en jamovi

10.7 La prueba de McNemar

Supongamos que te han contratado para trabajar para el Partido Político Genérico Australiano (PPGA), y parte de tu trabajo consiste en averiguar la eficacia de los anuncios políticos del PPGA. Así que decides reunir una muestra de $N = 100$ personas y pedirles que vean los anuncios de AGPP. Antes de que vean nada, les preguntas si tienen intención de votar al PPGA, y después de ver los anuncios, les vuelves a preguntar para ver si alguien ha cambiado de opinión. Obviamente, si eres buena en tu trabajo, también harías muchas otras cosas, pero consideremos sólo este sencillo experimento. Una forma de describir los datos es mediante la tabla de contingencia que se muestra en Table 10.11.

Table 10.11:
Tabla de contingencia con datos de anuncios políticos del PPGA
	Before	After	Total
Yes	30	10	40
No	70	90	160
Total	100	100	200

A primera vista, se podría pensar que esta situación se presta a la prueba de independencia $\chi^2$ de Pearson (según La prueba de independencia (o asociación) $\chi^2$). Sin embargo, un poco de reflexión revela que tenemos un problema. Tenemos 100 participantes, pero 200 observaciones. Esto se debe a que cada persona nos ha proporcionado una respuesta tanto en la columna del antes como en la del después. Esto significa que las 200 observaciones no son independientes entre sí. Si el votante A dice “sí” la primera vez y el votante B dice “no”, entonces es de esperar que el votante A tenga más probabilidades de decir “sí” la segunda vez que el votante B. La consecuencia de esto es que la prueba habitual $\chi^2$ no dará respuestas fiables debido a la violación del supuesto de independencia. Ahora bien, si esta fuera una situación realmente poco común, no me molestaría en hacerte perder el tiempo hablando de ella. Pero no es poco común en absoluto. Este es un diseño estándar de medidas repetidas, y ninguna de las pruebas que hemos considerado hasta ahora puede manejarlo.

La solución al problema fue publicada por McNemar (1947). El truco consiste en comenzar tabulando los datos de una forma ligeramente distinta (Table 10.12).

Table 10.12:
tabula los datos de una manera diferente cuando tienes datos de medidas repetidas
	Before: Yes	Before: No	Total
After: Yes	5	5	10
After: No	25	65	90
Total	30	70	100

A continuación, pensemos en cuál es nuestra hipótesis nula: es que la prueba del “antes” y la prueba del “después” tienen la misma proporción de personas que dicen “Sí, votaré por PPGA”. Debido a la forma en que hemos reescrito los datos, significa que ahora estamos probando la hipótesis de que los totales de fila y los totales de columna provienen de la misma distribución. Así, la hipótesis nula en la prueba de McNemar es que tenemos “homogeneidad marginal”. Es decir, que los totales de fila y los totales de columna tienen la misma distribución: $P_a + P_b = P_a + P_c$ y de manera similar que $P_c + P_d = P_b + P_d$. Observa que esto significa que la hipótesis nula en realidad se simplifica a Pb = Pc. En otras palabras, en lo que respecta a la prueba de McNemar, ¡solo importan las entradas fuera de la diagonal de esta tabla (es decir, b y c)! Después de observar esto, la prueba de homogeneidad marginal de McNemar no es diferente a una prueba habitual de $\chi^2$. Después de aplicar la corrección de Yates, nuestra prueba estadística se convierte en:

\[\chi^2=\frac{(|bc|-0.5)^2}{b+c}\] o, para volver a la notación que usamos anteriormente en este capítulo:

\[\chi^2=\frac{(|O_{12}-O_{21}|-0.5)^2}{O_{12}+O_{21}}\] y este estadístico tiene un $\chi^ 2$ (aproximadamente) con gl = 1. Sin embargo, recuerda que, al igual que las otras pruebas de $\chi^2$, es solo una aproximación, por lo que debes tener un número de recuentos esperados razonablemente grande para que funcione.

10.7.1 Haciendo la prueba de McNemar en jamovi

Ahora que ya sabes en qué consiste la prueba de McNemar, hagamos una. El archivo agpp.csv contiene los datos sin procesar de los que he hablado anteriormente. El conjunto de datos de agpp contiene tres variables, una variable de id que etiqueta a cada participante en el conjunto de datos (veremos por qué es útil en un momento), una variable response_before que registra la respuesta de la persona cuando se le hizo la pregunta la primera vez, y una variable response_after que muestra la respuesta que dio cuando se le hizo la misma pregunta por segunda vez. Ten en cuenta que cada participante aparece solo una vez en este conjunto de datos. Ves a ‘Análisis’ - ‘Frecuencias’ - ‘Tablas de contingencia’ - Análisis de ‘Muestras emparejadas’ en jamovi, y mueve response_before al cuadro ‘Rows’ y response_after al cuadro ‘Columns’. Obtendrás entonces una tabla de contingencia en la ventana de resultados, con el estadístico de la prueba de McNemar justo debajo, ver Figure 10.8.

Figure 10.8: salida de prueba de McNemar en jamovi

Y hemos terminado. Acabamos de realizar una prueba de McNemar para determinar si las personas tenían la misma probabilidad de votar PPGA después de los anuncios que antes. La prueba fue significativa ($\chi^2(1)= 12.03, p< .001)$, lo que sugiere que no lo fueron. Y, de hecho, parece que los anuncios tuvieron un efecto negativo: era menos probable que las personas votaran por el PPGA después de ver los anuncios. Lo cual tiene mucho sentido si consideras la calidad de un típico anuncio político.

10.8 ¿Cuál es la diferencia entre McNemar y la independencia?

Volvamos al principio del capítulo y examinemos de nuevo el conjunto de datos de las cartas. Si recuerdas, el diseño experimental real que describí implicaba que las personas hicieran dos elecciones. Como tenemos información sobre la primera elección y la segunda elección que todos hicieron, podemos construir la siguiente tabla de contingencia que compara la primera elección con la segunda elección (Table 10.13).

Table 10.13:
tabulación cruzada de la primera contra la segunda opción con los datos de Randomness.omv (cartas)
	Before: Yes	Before: No	Total
After: Yes	$a $	$b $	$a + b $
After: No	$c $	$d $	$c + d $
Total	$a+c $	$b+d $	$n $

Supongamos que quisiera saber si la elección que haces la segunda vez depende de la elección que hiciste la primera vez. Aquí es donde es útil una prueba de independencia, y lo que estamos tratando de hacer es ver si hay alguna relación entre las filas y las columnas de esta tabla.

Supongamos que quisiera saber si, en promedio, las frecuencias de las elecciones de palo fueron diferentes la segunda vez que la primera vez. En esa situación, lo que realmente estoy intentando ver es si los totales de las filas son diferentes de los totales de las columnas. Es entonces cuando se utiliza la prueba de McNemar.

En Figure 10.9 se muestran los diferentes estadísticos producidos por esos distintos análisis. ¡Observe que los resultados son diferentes! No se trata de la misma prueba.

Figure 10.9: Independiente vs. Emparejado (McNemar) con los datos de Randomness.omv (cartas)

10.9 Resumen

Las ideas clave discutidas en este capítulo son:

La prueba de bondad de ajuste $\chi^2$ (ji-cuadrado) se usa cuando tienes una tabla de frecuencias observadas de diferentes categorías, y la hipótesis nula te da un conjunto de probabilidades “conocidas” para compararlas.
La prueba de independencia (o asociación) $\chi^2$ se usa cuando se tiene una tabla de contingencia (tabulación cruzada) de dos variables categóricas. La hipótesis nula es que no existe relación o asociación entre las variables.
Tamaño del efecto para una tabla de contingencia se puede medir de varias maneras. En particular, observamos el estadístico $V$ de Cramer.
Ambas versiones de la prueba de Pearson se basan en dos supuestos: que las frecuencias esperadas son suficientemente grandes y que las observaciones son independientes (Supuestos de la(s) prueba(s). La prueba exacta de Fisher se puede usar cuando las frecuencias esperadas son pequeñas La prueba de McNemar se puede utilizar para algunos tipos de violaciones de la independencia.

Si estás interesada en obtener más información sobre el análisis de datos categóricos, una buena primera opción sería Agresti (1996) que, como sugiere el título, ofrece una Introducción al análisis de datos categóricos. Si el libro introductorio no es suficiente para ti (o no puedes resolver el problema en el que estás trabajando), podrías considerar Agresti (2002), Análisis de datos categóricos. Este último es un texto más avanzado, por lo que probablemente no sea prudente pasar directamente de este libro a aquel.

también conocido como “ji-cuadrado”.↩︎
un vector es una secuencia de elementos de datos del mismo tipo básico.↩︎
si hacemos que k se refiera al número total de categorías (es decir, k = 4 para los datos de nuestras cartas), entonces el estadístico $\chi^2$ está dado por: \[\chi^2 = \sum_{i=1}^{k} \frac{(O_i-E_i)^2}{E_i}\] Intuitivamente, está claro que si $chi^2$ es pequeño, entonces los datos observados Oi están muy cerca de lo que predijo la hipótesis nula $E_i$, por lo que vamos a necesitar un gran estadístico $\chi^2$ para rechazar la hipótesis nula.↩︎
si reescribes la ecuación para el estadístico de bondad de ajuste como una suma de k - 1 cosas independientes, obtienes la distribución muestral “adecuada”, que es ji-cuadrado con k - 1 grados de libertad. Está fuera del alcance de un libro introductorio mostrar las matemáticas con tanto detalle. Todo lo que quería hacer es darte una idea de por qué el estadístico de bondad de ajuste está asociado con la distribución de ji-cuadrado.↩︎
Me siento obligada a señalar que esto es una simplificación excesiva. Funciona bien en bastantes situaciones, pero de vez en cuando nos encontraremos con valores de grados de libertad que no son números enteros. No dejes que esto te preocupe demasiado; cuando te encuentres con esto, recuerda que los “grados de libertad” son en realidad un concepto un poco confuso, y que la bonita y simple historia que te estoy contando aquí no es toda la historia. Para una clase introductoria, por lo general es mejor ceñirse a la historia simple, pero creo que es mejor advertirte que esperes que esta historia simple se desmorone. Si no te hiciera esta advertencia, podrías comenzar a confundirte cuando veas $df = 3.4$ o algo así, pensando (incorrectamente) que has entendido mal algo de lo que te he enseñado en lugar de darte cuenta (correctamente) de que hay algo que no te he contado.↩︎
en la práctica, el tamaño de la muestra no siempre es fijo. Por ejemplo, podemos ejecutar el experimento durante un período fijo de tiempo y la cantidad de personas que participan depende de cuántas personas se presenten. Eso no importa para los propósitos actuales.↩︎
Bueno, más o menos. Las convenciones sobre cómo se deben presentarse las estadísticas tienden a diferir un poco de una disciplina a otra. He tendido a ceñirme a cómo se hacen las cosas en psicología, ya que es a lo que me dedico. Pero creo que el principio general de proporcionar suficiente información al lector para que pueda comprobar los resultados es bastante universal.↩︎
para algunas personas, este consejo puede sonar extraño, o al menos contradictorio con los consejos “habituales” sobre cómo redactar un informe técnico. Por lo general, a los estudiantes se les dice que la sección de “resultados” de un informe sirve para describir los datos e informar del análisis estadístico, y que la sección de “discusión” sirve para interpretarlos. Eso es cierto, pero creo que la gente suele interpretarlo de forma demasiado literal. Yo suelo hacer una interpretación rápida y sencilla de los datos en la sección de resultados, para que el lector entienda lo que nos dicen los datos. Luego, en la discusión, intento contar una historia más amplia sobre cómo mis resultados encajan con el resto de la literatura científica. En resumen, no dejes que el consejo de “la interpretación va en la discusión” convierta tu sección de resultados en una basura incomprensible. Ser entendido por tu lector es mucho más importante.↩︎
si has estado leyendo con mucha atención y eres una pedante matemática como yo, hay una cosa sobre la forma en que escribí la prueba de ji-cuadrado en la última sección que podría estar molestándote un poco. Hay algo que no cuadra al escribir “$\chi^2(3) = 8.44$”, estarás pensando. Después de todo, es el estadístico de bondad de ajuste lo que equivale a 8,44, así que ¿no debería haber escrito $X^2 = 8,44$ o tal vez $GOF = 8,44$? Esto parece combinar la distribución muestral (es decir, $\chi^2$ con gl = 3) con la prueba estadística (es decir, $X^2$). Lo más probable es que pensaras que era un error tipográfico, ya que $\chi$ y X se parecen bastante. Curiosamente, no lo es. Escribir $\chi^2$(3)= 8,44 es esencialmente una forma muy condensada de escribir “la distribución muestral de la prueba estadística es $\chi^2$(3). y el valor de la prueba estadística es 8,44”. En cierto sentido, esto es algo estúpido. Hay muchas pruebas estadísticas diferentes que resultan tener una distribución muestral de ji-cuadrado. El estadístico $X^2$ que hemos usado para nuestra prueba de bondad de ajuste es solo uno de muchos (aunque uno de los más comunes). En un mundo sensato y perfectamente organizado, siempre tendríamos un nombre distinto para la prueba estadística y la distribución muestral. De esa manera, el bloque de estadísticos en sí mismo te diría exactamente qué fue lo que calculó el investigador. A veces esto sucede. Por ejemplo, la prueba estadística utilizada en la prueba de bondad de ajuste de Pearson se escribe $X^2$ , pero hay una prueba estrechamente relacionada conocida como G-test$^a$ (Sokal & Rohlf, 1994), en la que la prueba estadística se escribe como $G$. Da la casualidad de que la prueba de bondad de ajuste de Pearson y la prueba G prueban la misma hipótesis nula, y la distribución muestral es exactamente la misma (es decir, ji-cuadrado con $k - 1$ grados de libertad). Si hubieras hecho una prueba G para los datos de las cartas en lugar de una prueba de bondad de ajuste, habrías terminado con una prueba estadística de $G = 8.65$, que es ligeramente diferente del valor $X^ 2 = 8,44 $ que obtuve antes y que produce un valor p ligeramente más pequeño de $p = 0,034 $. Supongamos que la convención fuera informar de la prueba estadística, luego la distribución muestral y luego el valor p. Si eso fuera cierto, estas dos situaciones producirían diferentes bloques de estadísticos: mi resultado original sería $X^2 = 8.44$, $\chi^2(3)$, $p = .038$, mientras que la nueva versión usando la prueba G se escribiría como $G = 8.65$, $\chi^2(3)$, $p = .034$. Sin embargo, la norma de información condensada, el resultado original se escribe $\chi^2(3) = 8.44, p =.038$, y el nuevo se escribe $\chi^2(3) = 8.65, p = . 034$, por lo que en realidad no está claro qué prueba realicé. Entonces, ¿por qué no vivimos en un mundo en el que el contenido del bloque de estadísticos especifica de forma única qué pruebas se realizaron? La razón profunda es que la vida es un lío. Nosotras (como usuarias de herramientas estadísticas) queremos que sea agradable, ordenada y organizada. Queremos que esté diseñada, como si fuera un producto, pero no es así como funciona la vida. La estadística es una disciplina intelectual tanto como cualquier otra, y como tal es un proyecto distribuido masivamente, en parte colaborativo y en parte competitivo que nadie realmente entiende por completo. Las cosas que tú y yo usamos como herramientas de análisis de datos no fueron creadas por un acto de los dioses de la estadística. Fueron inventadas por muchas personas diferentes, publicadas como artículos en revistas académicas, implementadas, corregidas y modificadas por muchas otras personas y luego explicadas a los estudiantes en libros de texto por otra persona. Como consecuencia, hay muchas pruebas estadísticas que ni siquiera tienen nombre y, como consecuencia, reciben el mismo nombre que la distribución muestral correspondiente. Como veremos más adelante, cualquier prueba estadística que siga una distribución $\chi^2$ se denomina comúnmente “estadístico ji-cuadrado”, cualquier estadístico que siga una distribución $t$ se denomina “estadístico t”, etcétera. Pero, como ilustra el ejemplo de $\chi^2$ versus $G$, dos cosas diferentes con la misma distribución muestral siguen siendo, bueno, diferentes. Como consecuencia, a veces es una buena idea tener claro cuál fue la prueba real que se ejecutó, especialmente si estás haciendo algo inusual. Si solo dices “prueba de ji-cuadrado”, en realidad no está claro de qué prueba estás hablando. Aunque, dado que las dos pruebas de ji-cuadrado más comunes son la prueba de bondad de ajuste y la prueba de independencia, la mayoría de los lectores con entrenamiento en estadística probablemente puedan adivinar. Sin embargo, es algo a tener en cuenta. – $^a$ Para complicar las cosas, la prueba G es un caso especial de toda una clase de pruebas que se conocen como pruebas de razón de verosimilitud. No cubro las pruebas de razón de verosimilitud en este libro, pero es muy útil conocerlas.↩︎
Nota técnica. La forma en que describí la prueba supone que los totales de las columnas son fijos (es decir, el investigador tenía la intención de encuestar a 87 robots y 93 humanos) y los totales de las filas son aleatorios (es decir, resulta que 28 personas eligieron el cachorro). Para usar la terminología de mi libro de texto de estadística matemáticas [@ Hogg2005], técnicamente debería referirme a esta situación como una prueba ji-cuadrado de homogeneidad y reservar el término prueba de independencia de ji-cuadrado para la situación en la que tanto los totales de fila como de columna son resultados aleatorios del experimento. En los borradores iniciales de este libro, eso es exactamente lo que hice. Sin embargo, resulta que estas dos pruebas son idénticas, por lo que las he unido.↩︎
Técnicamente, $E_{ij}$ aquí es una estimación, por lo que probablemente debería escribir $\hat{E_{ij}}$ . Pero como nadie más lo hace, yo tampoco lo haré.↩︎
Ahora que ya sabemos cómo calcular las frecuencias esperadas, es sencillo definir una prueba estadística, siguiendo exactamente la misma estrategia que usamos en la prueba de bondad de ajuste. De hecho, es prácticamente el mismo estadístico. Para una tabla de contingencia con r filas y c columnas, la ecuación que define nuestro estadístico $X^2$ es \[X^2=\sum_{i=1}^{r}\sum_{j=1}^{c } \frac{(E_{ij}-O_{ij})^2}{E_{ij}}\] La única diferencia es que tengo que incluir dos signos de suma (es decir, $\sum$ ) para indicar que estamos sumando sobre ambas filas y columnas.↩︎
un problema que a muchas nos preocupa en la vida real.↩︎
Yates (1934) sugirió una solución simple, en la que redefine el estadístico de bondad de ajuste como: \[\chi^{2}=\sum_{i}\frac{(|E_i-O_i|-0.5)^2}{E_i}\] Básicamente, solo resta 0.5 en todas partes.↩︎
Matemáticamente, son muy sencillos. Para calcular el estadístico $\phi$, basta con dividir el valor de $X^2$ por el tamaño de la muestra y sacar la raíz cuadrada: \[\phi=\sqrt{\frac{X^2}{N}}\] La idea es que el estadístico $\phi$ oscila entre 0 (ninguna asociación) y 1 (asociación perfecta), pero no siempre lo hace cuando la tabla de contingencia es mayor que $2 $, lo que es un auténtico incordio. Para tablas más grandes, es posible obtener $\phi > 1$, lo cual es bastante insatisfactorio. Así que, para corregir esto, la gente suele preferir informar el estadístico $V$ propuesto por Cramer (1946). Es un ajuste bastante simple de $\phi$. Si tienes una tabla de contingencia con r filas y c columnas, defines $k = min(r, c)$ como el menor de los dos valores. Si es así, entonces el estadístico $V$ de Cramer es \[V=\sqrt{\frac{X^2}{N(k-1)}}\]↩︎
Este ejemplo se basa en un artículo de broma publicado en el Journal of Irreproducible Results↩︎
No es sorprendente que la prueba exacta de Fisher esté motivada por la interpretación de Fisher de un valor p, ¡no por la de Neyman! Consulta Section 9.5.↩︎

	Robot	Human	Total
Puppy	\(O_{11}\)	\(O_{12}\)	\(R_{1}\)
Flower	\(O_{21}\)	\(O_{22}\)	\(R_{2}\)
Data	\(O_{31}\)	\(O_{32}\)	\(R_{3}\)
Total	\(C_{1}\)	\(C_{2}\)	N

	Happy	Sad	Total
Set on fire	\(O_{11}\)	\(O_{12}\)	\(R_{1}\)
Not set on fire	\(O_{21}\)	\(O_{22}\)	\(R_{2}\)
Total	\(C_{1}\)	\(C_{2}\)	\(N\)

	Before: Yes	Before: No	Total
After: Yes	\(a \)	\(b \)	\(a + b \)
After: No	\(c \)	\(d \)	\(c + d \)
Total	\(a+c \)	\(b+d \)	\(n \)