
13 Comparación de varias medias (ANOVA unidireccional)
Este capítulo presenta una de las herramientas más utilizadas en estadística psicológica, conocida como “análisis de la varianza”, pero generalmente denominada ANOVA. La técnica básica fue desarrollada por Sir Ronald Fisher a principios del siglo XX y es a él a quien le debemos la terminología bastante desafortunada. El término ANOVA es un poco engañoso, en dos aspectos. En primer lugar, aunque el nombre de la técnica se refiere a las varianzas, ANOVA se ocupa de investigar las diferencias en las medias. En segundo lugar, hay diferentes cosas que se conocen como ANOVA, algunas de las cuales tienen poca relación. Más adelante en el libro, encontraremos diferentes métodos ANOVA que se aplican en situaciones bastante diferentes, pero para los propósitos de este capítulo solo consideraremos la forma más simple de ANOVA, en la que tenemos varios grupos diferentes de observaciones, y nos interesa averiguar si esos grupos difieren en términos de alguna variable de resultado de interés. Esta es la pregunta que se aborda mediante un ANOVA unifactorial.
La estructura de este capítulo es la siguiente: primero presentaré un conjunto de datos ficticios que usaremos como ejemplo a lo largo del capítulo. Después de presentar los datos, describiré la mecánica de cómo funciona realmente un ANOVA unifactorial Cómo funciona ANOVA y luego me centraré en cómo puedes ejecutar uno en jamovi [Ejecutar un ANOVA en jamovi]. Estas dos secciones son el núcleo del capítulo.
El resto del capítulo analiza algunos temas importantes que inevitablemente surgen cuando se ejecuta un ANOVA, a saber, cómo calcular los tamaños del efecto, las pruebas post hoc y las correcciones para comparaciones múltiples y los supuestos en las que se basa el ANOVA. También hablaremos sobre cómo verificar esos supuestos y algunas de las cosas que puedes hacer si se violan los supuestos. Luego hablaremos de ANOVA de medidas repetidas.
13.1 Un conjunto de datos ilustrativos
Imagina que llevas a cabo un ensayo clínico en el que estás probando un nuevo fármaco antidepresivo llamado Joyzepam. Con el fin de construir una prueba justa de la eficacia del fármaco, el estudio implica la administración de tres fármacos separados. Uno es un placebo y el otro es un medicamento antidepresivo/ansiolítico existente llamado Anxifree. Se reclutan 18 participantes con depresión moderada a severa para la prueba inicial. Debido a que los fármacos a veces se administran junto con la terapia psicológica, tu estudio incluye a 9 personas que se someten a terapia cognitiva conductual (TCC) y 9 que no la reciben. A los participantes se les asigna aleatoriamente (doble ciego, por supuesto) un tratamiento, de modo que haya 3 personas con TCC y 3 personas sin terapia asignadas a cada uno de los 3 medicamentos. Un psicólogo evalúa el estado de ánimo de cada persona después de 3 meses de tratamiento con cada medicamento, y la mejora general en el estado de ánimo de cada persona se evalúa en una escala que va de \(-5\) a \(+5\). Con ese diseño del estudio, ahora carguemos el archivo de datos en Clinicaltrial.csv. Podemos ver que este conjunto de datos contiene las tres variables fármaco, terapia y humor.ganancia.
Para los objetivos de este capítulo, lo que realmente nos interesa es el efecto de los fármacos sobre el estado de ánimo. Lo primero que debes hacer es calcular algunos estadísticos descriptivos y dibujar algunos gráficos. En el capítulo Chapter 4 te mostramos cómo hacer esto, y algunos de los estadísticos descriptivos que podemos calcular en jamovi se muestran en Figure 13.1
Como el gráfico muestra, hay una mayor mejora en el estado de ánimo de los participantes en el grupo de Joyzepam que en el grupo de Anxifree o en el grupo de placebo. El grupo Anxifree muestra una mayor mejora del estado de ánimo que el grupo de control, pero la diferencia no es tan grande. La pregunta que queremos responder es si estas diferencias son “reales” o solo se deben al azar.
13.2 Cómo funciona ANOVA
Para responder a la pregunta planteada por los datos de nuestro ensayo clínico, vamos a ejecutar un ANOVA unifactorial. Comenzaré mostrándote cómo hacerlo de la manera difícil, construyendo la herramienta estadística desde cero y mostrándote cómo podrías hacerlo si no tuvieras acceso a ninguna de las geniales funciones de ANOVA integradas en jamovi. Y espero que lo leas atentamente, intenta hacerlo de la manera larga una o dos veces para asegurarte de que realmente comprendes cómo funciona ANOVA, y luego, una vez que hayas comprendido el concepto, nunca vuelvas a hacerlo de esta manera.
El diseño experimental que describí en la sección anterior sugiere que nos interesa comparar el cambio de estado de ánimo promedio para los tres fármacos diferentes. En ese sentido, estamos hablando de un análisis similar a la prueba t (ver Chapter 11) pero involucrando a más de dos grupos. Si hacemos que \(\mu_P\) denote la media de la población para el cambio de estado de ánimo inducido por el placebo, y que \(\mu_A\) y \(\mu_J\) denote las medias correspondientes para nuestros dos fármacos, Anxifree y Joyzepam, entonces la (algo pesimista) hipótesis nula que queremos probar es que las medias de las tres poblaciones son idénticas. Es decir, ninguno de los dos fármacos es más efectivo que un placebo. Podemos escribir esta hipótesis nula como:
\[H_0: \text{ es cierto que } \mu_P=\mu_A=\mu_J\]
Como consecuencia, nuestra hipótesis alternativa es que al menos uno de los tres tratamientos es diferente de los demás. Es un poco complicado escribir esto matemáticamente, porque (como veremos) hay bastantes maneras diferentes en las que la hipótesis nula puede ser falsa. Así que por ahora escribiremos la hipótesis alternativa así:
\[H_1: \text{ eso } \underline{ es \text{ } no } \text{ es cierto que } \mu_P=\mu_A=\mu_J\]
Esta hipótesis nula es mucho más difícil de probar que cualquiera de las que hemos visto anteriormente. ¿Cómo lo haremos? Una forma sensata sería “hacer un ANOVA”, ya que ese es el título del capítulo, pero no está particularmente claro por qué un “análisis de varianzas” nos ayudará a aprender algo útil sobre las medias. De hecho, esta es una de las mayores dificultades conceptuales que tienen las personas cuando se encuentran por primera vez con ANOVA. Para ver cómo funciona, me parece más útil comenzar hablando de variancias, específicamente variabilidad entregrupo y variabilidad intragrupo (Figure 13.2).

13.2.1 Dos fórmulas para la varianza de Y
En primer lugar, comencemos introduciendo algo de notación. Usaremos G para referirnos al número total de grupos. Para nuestro conjunto de datos hay tres fármacos, por lo que hay \(G = 3\) grupos. A continuación, usaremos \(N\) para referirnos al tamaño total de la muestra; hay un total de \(N = 18\) personas en nuestro conjunto de datos. De manera similar, usemos \(N_k\) para indicar el número de personas en el k-ésimo grupo. En nuestro ensayo clínico falso, el tamaño de la muestra es \(N_k = 6\) para los tres grupos.1 Finalmente, usaremos Y para indicar la variable de resultado. En nuestro caso, Y se refiere al cambio de estado de ánimo. Específicamente, usaremos Yik para referirnos al cambio de estado de ánimo experimentado por el i-ésimo miembro del k-ésimo grupo. De manera similar, usaremos \(\bar{Y}\) para el cambio de estado de ánimo promedio, recogido entre las 18 personas en el experimento, y \(\bar{Y}_k\) para referirnos al cambio de estado de ánimo promedio experimentado por las 6 personas en el grupo \(k\).
Ahora que hemos resuelto nuestra notación, podemos comenzar a escribir fórmulas. Para empezar, recordemos la fórmula para la varianza que usamos en Section 4.2, en aquellos días más amables cuando solo hacíamos estadística descriptiva. La varianza muestral de Y se define de la siguiente manera \[Var(Y)=\frac{1}{N}\sum_{k=1}^{G}\sum_{i=1}^{N_k}(Y_{ik }-\bar{Y})^2\] Esta fórmula parece bastante idéntica a la fórmula para la varianza en Section 4.2. La única diferencia es que ahora tengo dos sumas aquí: estoy sumando entre grupos (es decir, valores para \(k\)) y las personas dentro de los grupos (es decir, valores para \(i\)). Esto es puramente un detalle cosmético. Si, en cambio, hubiera usado la notación \(Y_p\) para referirme al valor de la variable de resultado para la persona p en la muestra, tendría una sola suma. La única razón por la que tenemos una suma doble aquí es porque clasifiqué a las personas en grupos y luego asigné números a las personas dentro de los grupos.
Un ejemplo concreto podría sernos útil. Consideremos Table 13.1, en el que tenemos un total de \(N = 5\) personas clasificadas en \(G = 2\) grupos. Arbitrariamente, digamos que las personas “geniales” son el grupo 1 y las personas “no geniales” son el grupo 2. Resulta que tenemos tres personas geniales (\(N_1 = 3\)) y dos personas no geniales (\(N_2 = 2\))
| name | person P | group | group num. k | index in group | grumpiness \( Y_{ik} \) or \( Y_p \) |
|---|---|---|---|---|---|
| Ann | 1 | cool | 1 | 1 | 20 |
| Ben | 2 | cool | 1 | 2 | 55 |
| Cat | 3 | cool | 1 | 3 | 21 |
| Tim | 4 | uncool | 2 | 1 | 91 |
| Egg | 5 | uncool | 2 | 2 | 22 |
Ten en cuenta que he construido dos esquemas de etiquetado diferentes aquí. Tenemos una variable de “persona” p, por lo que sería perfectamente sensato referirse a Yp como el mal humor de la p-ésima persona en la muestra. Por ejemplo, la tabla muestra que Tim es el cuarto, entonces diríamos \(p = 4\). Así, cuando hablamos del mal humor \(Y\) de esta persona “Tim”, quienquiera que sea, podríamos referirnos a su mal humor diciendo que \(Y_p = 91\), para la persona \(p = 4\). Sin embargo, esa no es la única forma en que podemos referirnos a Tim. Como alternativa, podemos señalar que Tim pertenece al grupo “no geniales” (\(k = 2\)) y, de hecho, es la primera persona que figura en el grupo no geniales (\(i = 1\)). Así que es igualmente válido referirse al mal humor de Tim diciendo que \(Y_{ik} = 91\), donde \(k = 2\) y \(i = 1\).
En otras palabras, cada persona p corresponde a una única combinación ik, por lo que la fórmula que di arriba es en realidad idéntica a nuestra fórmula original para la varianza, que sería \[Var(Y)=\frac{1}{N }\sum_{p=1}^{N}(Y_p-\bar{Y})^2\] En ambas fórmulas, lo único que hacemos es sumar todas las observaciones de la muestra. La mayoría de las veces solo usaríamos la notación Yp más simple; la ecuación que usa \(Y_p\) es claramente la más simple de las dos. Sin embargo, al hacer un ANOVA es importante hacer un seguimiento de qué participantes pertenecen a qué grupos, y necesitamos usar la notación Yik para hacer esto.
13.2.2 De varianzas a sumas de cuadrados
Bien, ahora que sabemos cómo se calcula la varianza, definamos algo llamado suma de cuadrados total , que se denota como SCtot. Es muy simple. En lugar de promediar las desviaciones al cuadrado, que es lo que hacemos cuando calculamos la varianza, simplemente las sumamos.2
Cuando hablamos de analizar las varianzas en el contexto de ANOVA, lo que realmente estamos haciendo es trabajar con las sumas de cuadrados totales en lugar de la varianza real. 3
A continuación, podemos definir una tercera noción de variación que recoge solo las diferencias entre grupos. Hacemos esto observando las diferencias entre las medias de grupo \(\bar{Y}_k\) y la media total \(\bar{Y}\). 4
No es difícil mostrar que la variación total entre las personas en el experimento (\(SS_{tot}\) es en realidad la suma de las diferencias entre los grupos \(SS_b\) y la variación dentro de los grupos \(SS_w\). Es decir,
\[SS_w+SS_b=SS_{tot}\] Sí.
Bien, entonces, ¿qué hemos descubierto? Hemos descubierto que la variabilidad total asociada con la variable de resultado (\(SS_{tot}\)) se puede dividir matemáticamente en la suma de “la variación debida a las diferencias en las medias de la muestra para los diferentes grupos” (\(SS_b\) ) más “todo el resto de la variación” (\(SS_w\)) 5.
¿Cómo me ayuda eso a averiguar si los grupos tienen diferentes medias poblacionales? Um. Espera. Espera un segundo. Ahora que lo pienso, esto es exactamente lo que estábamos buscando. Si la hipótesis nula es verdadera, esperaría que todas las medias de la muestra fueran bastante similares entre sí, ¿verdad? Y eso implicaría que esperaría que el valor de \(SS_b\) fuera realmente pequeño, o al menos esperaría que fuera mucho más pequeño que “la variación asociada con todo lo demás”, \(SS_w\). Mmm. Detecto que se acerca una prueba de hipótesis.
13.2.3 De sumas de cuadrados a la prueba F
Como vimos en la última sección, la idea detrás de ANOVA es comparar los valores de dos sumas de cuadrados \(SS_b\) y \(SS_w\) entre sí. Si la variación entre grupos \(SS_b\) es grande en relación con la variación dentro del grupo \(SS_w\), entonces tenemos razones para sospechar que las medias poblacionales para los diferentes grupos no son idénticas entre sí. Para convertir esto en una prueba de hipótesis viable, se necesita “jugar” un poco. Lo que haré será mostrarte primero lo que hacemos para calcular nuestra prueba estadística, la razón de F, y luego trataré de darte una idea de por qué lo hacemos de esta manera.
Para convertir nuestros valores SC en una razón de F, lo primero que debemos calcular son los grados de libertad asociados con los valores \(SS_b\) y \(SS_w\). Como es habitual, los grados de libertad corresponden al número de “datos” únicos que contribuyen a un cálculo particular, menos el número de “restricciones” que deben satisfacer. Para la variabilidad dentro de los grupos, lo que estamos calculando es la variación de las observaciones individuales (\(N\) datos) alrededor de las medias del grupo (\(G\) restricciones). Por el contrario, para la variabilidad entre grupos, nos interesa la variación de las medias de los grupos (datos G) alrededor de la media total (restricción 1). Por lo tanto, los grados de libertad aquí son:
\[df_b=G-1\] \[df_w=NG\]
Bueno, eso parece bastante simple. Lo que hacemos a continuación es convertir nuestro valor de sumas de cuadrados en un valor de “medias cuadráticas”, lo que hacemos dividiendo por los grados de libertad:
\[MS_b=\frac{SS_b}{df_b}\] \[MS_w=\frac{SS_w}{df_w}\]
Finalmente, calculamos la razón F dividiendo la MC entre grupos por la MC intra grupos:
\[F=\frac{MS_b}{MS_w}\]
A un nivel muy general, la explicación del estadístico F es sencilla. Los valores más grandes de F significan que la variación entre grupos es grande en relación con la variación dentro de los grupos. Como consecuencia, cuanto mayor sea el valor de F, más evidencia tendremos en contra de la hipótesis nula. Pero, ¿qué tamaño tiene que tener \(F\) para rechazar realmente \(H_0\)? Para comprender esto, necesitas una comprensión un poco más profunda de qué es ANOVA y cuáles son realmente los valores de las medias cuadráticas.
La siguiente sección trata eso con un poco de detalle, pero para quien no tenga interés en los detalles de lo que realmente mide la prueba, iré al grano. Para completar nuestra prueba de hipótesis, necesitamos conocer la distribución muestral de F si la hipótesis nula es verdadera. No es sorprendente que la distribución muestral para el estadístico F bajo la hipótesis nula sea una distribución \(F\). Si recuerdas nuestra discusión sobre la distribución F en Chapter 7, la distribución \(F\) tiene dos parámetros, correspondientes a los dos grados de libertad involucrados. El primero \(df_1\) son los grados de libertad entre grupos \(df_b\), y el segundo \(df_2\) son los grados de libertad intra grupos \(df_w\).
| between groups | within groups | |
|---|---|---|
| df | \( df_b=G-1 \) | \( df_w=N-G \) |
| sum of squares | \( SS_b=\sum_{k=1}^{G} N_k (\bar{Y}_k-\bar{Y})^2 \) | \( SS_w=\sum_{k=1}^{G} \sum_{i=1}^{N_k} (Y_{ik}-\bar{Y}_k)^2 \) |
| mean squares | \( MS_b=\frac{SS_b}{df_b} \) | \( MS_w=\frac{SS_w}{df_w} \) |
| F-statistic | \( F=\frac{MS_b}{df_b} \) | - |
| p-value | [complicated] | - |
En Table 13.2 se muestra un resumen de todas las cantidades clave involucradas en un ANOVA unifactorial, incluidas las fórmulas que muestran cómo se calculan.
[Detalle técnico adicional 6]
13.2.4 Un ejemplo resuelto
La discusión anterior fue bastante abstracta y un poco técnica, por lo que creo que en este punto podría ser útil ver un ejemplo resuelto. Para ello, volvamos a los datos de los ensayos clínicos que introduje al principio del capítulo. Los estadísticos descriptivos que calculamos al principio nos dicen las medias de nuestro grupo: una mejora promedio en el estado de ánimo de $ 0.45 $ para el placebo, $ 0.72 $ para Anxifree y $ 1.48 $ para Joyzepam. Con eso en mente, imaginemos que estamos en 1899 7 y comencemos haciendo algunos cálculos con lápiz y papel. Solo haré esto para las primeras observaciones de \(5\) porque no estamos en \(1899\) y soy muy vaga. Comencemos por calcular \(SS_w\), las sumas de cuadrados intra grupo. Primero, elaboremos una tabla para ayudarnos con nuestros cálculos (Table 13.3)
| group k | outcome \( Y_{ik} \) |
|---|---|
| placebo | 0.5 |
| placebo | 0.3 |
| placebo | 0.1 |
| anxifree | 0.6 |
| anxifree | 0.4 |
En este punto, lo único que he incluido en la tabla son los datos sin procesar. Es decir, la variable de agrupación (el fármaco) y la variable de resultado (el estado de ánimo.ganancia) para cada persona. Ten en cuenta que la variable de resultado aquí corresponde al valor \(\bar{Y}_{ik}\) en nuestra ecuación anterior. El próximo paso en el cálculo es anotar, para cada persona en el estudio, la media del grupo correspondiente, \(\bar{Y}_k\). Esto es un poco repetitivo pero no particularmente difícil dado que ya calculamos esas medias de grupo al hacer nuestros estadísticos descriptivos, ver Table 13.4.
| group k | outcome \( Y_{ik} \) | group mean \( \bar{Y}_k \) |
|---|---|---|
| placebo | 0.5 | 0.45 |
| placebo | 0.3 | 0.45 |
| placebo | 0.1 | 0.45 |
| anxifree | 0.6 | 0.72 |
| anxifree | 0.4 | 0.72 |
Ahora que los hemos escrito, necesitamos calcular, nuevamente para cada persona, la desviación de la media del grupo correspondiente. Es decir, queremos restar \(Y_{ik} - \bar{Y}_k\). Después de haber hecho eso, necesitamos elevar todo al cuadrado. Cuando hacemos eso, esto es lo que obtenemos (Table 13.5)
| group k | outcome \( Y_{ik} \) | group mean \( \bar{Y}_k \) | dev. from group mean \( Y_{ik} - \bar{Y}_k \) | squared deviation \( (Y_{ik}-\bar{Y}_k)^2 \) |
|---|---|---|---|---|
| placebo | 0.5 | 0.45 | 0.05 | 0.0025 |
| placebo | 0.3 | 0.45 | -0.15 | 0.0225 |
| placebo | 0.1 | 0.45 | -0.35 | 0.1225 |
| anxifree | 0.6 | 0.72 | -0.12 | 0.0136 |
| anxifree | 0.4 | 0.72 | -0.32 | 0.1003 |
El último paso es igualmente sencillo. Para calcular la suma de cuadrados intra grupo, simplemente sumamos las desviaciones al cuadrado de todas las observaciones:
\[ \begin{split} SS_w & = 0.0025 + 0.0225 + 0.1225 + 0.0136 + 0.1003 \\ & = 0.2614 \end{split} \]
Por supuesto, si realmente quisiéramos obtener la respuesta correcta, tendríamos que hacer esto para las 18 observaciones en el conjunto de datos, no solo para las primeras cinco. Podríamos continuar con los cálculos de lápiz y papel si quisiéramos, pero es bastante tedioso. Como alternativa, no es demasiado difícil hacer esto en una hoja de cálculo como OpenOffice o Excel. Inténtalo y hazlo tú misma. El que hice yo, en Excel, está en el archivo clinictrial_anova.xls. Cuando lo hagas, deberías terminar con un valor de suma de cuadrados intra grupo de $ 1.39 $.
Bueno. Ahora que hemos calculado la variabilidad intra grupos, \(SS_w\), es hora de centrar nuestra atención en la suma de cuadrados entre grupos, \(SS_b\). Los cálculos aquí son muy similares. La principal diferencia es que en lugar de calcular las diferencias entre una observación Yik y una media de grupo \(\bar{Y}_k\) para todas las observaciones, calculamos las diferencias entre las medias de grupo \(\bar{Y}_k\) y la media general \(\bar{Y}\) (en este caso \(0.88\)) para todos los grupos (Table 13.6).
| group k | group mean \( \bar{Y}_k \) | grand mean \( \bar{Y} \) | deviation \( \bar{Y}_k - \bar{Y} \) | squared deviation \( ( \bar{Y}_k-\bar{Y})^2 \) |
|---|---|---|---|---|
| placebo | 0.45 | 0.88 | -0.43 | 0.19 |
| anxifree | 0.72 | 0.88 | -0.16 | 0.03 |
| joyzepam | 1.48 | 0.88 | 0.60 | 0.36 |
Sin embargo, para los cálculos entre grupos necesitamos multiplicar cada una de estas desviaciones al cuadrado por \(N_k\), el número de observaciones en el grupo. Hacemos esto porque cada observación en el grupo (todas las \(N_k\)) está asociada con una diferencia entre grupos. Así, si hay seis personas en el grupo de placebo y la media del grupo de placebo difiere de la media general en $0,19 $, entonces la variación total entre grupos asociada con estas seis personas es $6 ,19 = 1,14 $. Así que tenemos que ampliar nuestra tabla de cálculos (Table 13.7).
| group k | ... | squared deviations \( (\bar{Y}_k-\bar{Y})^2 \) | sample size \( N_k \) | weighted squared dev \( N_k (\bar{Y}_k-\bar{Y})^2 \) |
|---|---|---|---|---|
| placebo | ... | 0.19 | 6 | 1.14 |
| anxifree | ... | 0.03 | 6 | 0.18 |
| joyzepam | ... | 0.36 | 6 | 2.16 |
Y ahora nuestra suma de cuadrados entre grupos se obtiene sumando estas “desviaciones cuadráticas ponderadas” sobre los tres grupos en el estudio:
\[\begin{aligned} SS_b & = 1.14 + 0.18 + 2.16 \\ &= 3.48 \end{aligned}\]
Como puedes ver, los cálculos entre grupos son mucho más cortos8. Ahora que hemos calculado nuestros valores de sumas de cuadrados, \(SS_b\) y \(SS_w\), el resto del ANOVA es bastante sencillo. El siguiente paso es calcular los grados de libertad. Como tenemos \(G = 3\) grupos y \(N = 18\) observaciones en total, nuestros grados de libertad se pueden calcular mediante una simple resta:
\[ \begin{split} df_b & = G-1 = 2 \\ df_w & = NG = 15 \end{split} \]
A continuación, dado que ahora hemos calculado los valores de las sumas de cuadrados y los grados de libertad, tanto para la variabilidad intra grupos como para la variabilidad entre grupos, podemos obtener los valores de las medias cuadráticas dividiendo uno por el otro:
\[ \begin{split} MS_b & = \frac{SS_b}{df_b} = \frac{3.48}{2} = 1.74 \\ MS_w & = \frac{SS_w}{df_w} = \frac{1.39}{15} = 0.09 \end{split} \]
Ya casi hemos terminado. Las medias cuadráticas se pueden usar para calcular el valor F, que es la prueba estadística que nos interesa. Hacemos esto dividiendo el valor de MC entre grupos por el valor de MC intra grupos.
\[ \begin{split} F & = \frac{MS_b}{MS_w} = \frac{1.74}{0.09} \\ & = 19,3 \end{split} \]
¡Guauuu! Esto es muy emocionante, ¿verdad? Ahora que tenemos nuestra prueba estadística, el último paso es averiguar si la prueba en sí nos da un resultado significativo. Como se discutió en Chapter 9 en los “viejos tiempos”, lo que haríamos sería abrir un libro de texto de estadística o pasar a la sección posterior que en realidad tendría una tabla de búsqueda enorme y encontraríamos el valor umbral \(F\) correspondiente a un valor particular de alfa (la región de rechazo de la hipótesis nula), por ejemplo \(0,05\), \(0,01\) o \(0,001\), para 2 y 15 grados de libertad. Hacerlo de esta manera nos daría un valor umbral de F para un alfa de \(0.001\) de \(11.34\). Como esto es menor que nuestro valor \(F\) calculado, decimos que \(p < 0.001\). Pero esos era antes, y ahora el sofisticado software de estadística calcula el valor p exacto por ti. De hecho, el valor p exacto es \(0.000071\). Entonces, a menos que estemos siendo extremadamente conservadores con respecto a nuestra tasa de error Tipo I, estamos prácticamente seguras de que podemos rechazar la hipótesis nula.
En este punto, básicamente hemos terminado. Habiendo completado nuestros cálculos, es tradicional organizar todos estos números en una tabla ANOVA como la de la Tabla 13.1. Para los datos de nuestro ensayo clínico, la tabla ANOVA se vería como Table 13.8.
| df | sum of squares | mean squares | F-statistic | p-value | |
|---|---|---|---|---|---|
| between groups | 2 | 3.48 | 1.74 | 19.3 | 0.000071 |
| within groups | 15 | 1.39 | 0.09 | - | - |
En estos días, probablemente no querrás construir una de estas tablas tú misma, pero encontrarás que casi todo el software estadístico (incluido jamovi) tiende a organizar la salida de un ANOVA en una tabla como esta, por lo que es una buena idea para acostumbrarse a leerlas. Sin embargo, aunque el software generará una tabla ANOVA completa, casi nunca se incluye la tabla completa en tu redacción. Una forma bastante estándar de informar del apartado de estadística sería escribir algo como esto:
ANOVA de un factor mostró un efecto significativo de la droga en el estado de ánimo (F(2,15) = 19.3, p < .001).
Ains. Tanto trabajo para una frase corta.
13.3 Ejecutando un ANOVA en jamovi
Estoy bastante segura de saber lo que estás pensando después de leer la última sección, especialmente si seguiste mi consejo e hiciste todo eso con lápiz y papel (es decir, en una hoja de cálculo) tú misma. Hacer los cálculos de ANOVA tú misma apesta. Hay muchos cálculos que necesitamos hacer en el camino, y sería tedioso tener que hacer esto una y otra vez cada vez que quisieras hacer un ANOVA.
13.3.1 Uso de jamovi para especificar tu ANOVA
Para facilitarte la vida, jamovi puede hacer ANOVA… ¡hurra! Ves a ‘ANOVA’ - Análisis ‘ANOVA’ y mueve la variable mood.gain para que esté en el cuadro ‘Variable dependiente’, y luego mueve la variable de fármaco para que esté en el cuadro ‘Factores fijos’. Esto debería dar los resultados como se muestra en Figure 13.3. 9 Ten en cuenta que también marqué la casilla de verificación \(\eta^2\), pronunciada “eta” al cuadrado, en la opción ‘Tamaño del efecto’ y esto también se muestra en la tabla de resultados. Volveremos a los tamaños del efecto un poco más tarde.

La tabla de resultados de jamovi te muestra los valores de las sumas de cuadrados, los grados de libertad y un par de otras cantidades que no nos interesan en este momento. Ten en cuenta, sin embargo, que jamovi no usa los nombres “entre grupos” y “intra grupo”. En su lugar, intenta asignar nombres más significativos. En nuestro ejemplo particular, la varianza entre grupos corresponde al efecto que el fármaco tiene sobre la variable de resultado, y la varianza intra grupos corresponde a la variabilidad “sobrante”, por lo que se denomina residual. Si comparamos estos números con los números que calculé a mano en [Un ejemplo práctico], puedes ver que son más o menos iguales, aparte de los errores de redondeo. La suma de cuadrados entre grupos es \(SS_b = 3.45\), la suma de cuadrados intra grupos es \(SS_w = 1.39\), y los grados de libertad son \(2\) y \(15\) respectivamente. También obtenemos el valor F y el valor p y, nuevamente, estos son más o menos iguales, sumando o restando errores de redondeo, a los números que calculamos nosotras mismas al hacerlo de la manera larga y tediosa.
13.4 Tamaño del efecto
Hay algunas formas diferentes de medir el tamaño del efecto en un ANOVA, pero las medidas más utilizadas son \(\eta^2\) (eta al cuadrado) y \(\eta^2\) parcial. Para un análisis de varianza unifactorial, son idénticos entre sí, así que por el momento solo explicaré \(\eta^2\) . La definición de \(\eta^2\) es realmente muy simple
\[\eta^2=\frac{SS_b}{SS_{total}}\]
Eso es todo. Entonces, cuando miro la tabla ANOVA en Figure 13.3, veo que \(SS_b = 3,45\) y \(SS_tot = 3,45 + 1,39 = 4,84\). Así obtenemos un valor de \(\eta^2\) de
\[\eta^2=\frac{3.45}{4.84}=0.71\]
La interpretación de \(\eta^2\) es igualmente sencilla. Se refiere a la proporción de la variabilidad en la variable de resultado (mood.gain) que se puede explicar en términos del predictor (fármaco). Un valor de \(\eta^2=0\) significa que no existe ninguna relación entre los dos, mientras que un valor de \(\eta^2=1\) significa que la relación es perfecta. Mejor aún, el valor de \(\eta^2\) está muy relacionado con \(R^2\), como se explicó anteriormente en Section 12.6.1, y tiene una interpretación equivalente. Aunque muchos libros de texto de estadística sugieren \(\eta^2\) como la medida predeterminada del tamaño del efecto en ANOVA, hay una <a href=“https://daniellakens.blogspot.com/2015/06/why-you-should-use” interesante. -omega-squared.html” target=“_blank”>entrada de blog de Daniel Lakens que sugiere que eta cuadrado quizás no sea la mejor medida del tamaño del efecto en el análisis de datos del mundo real, porque puede ser un estimador sesgado. Acertadamente, también hay una opción en jamovi para especificar omega-cuadrado (\(\omega^2\)), que es menos sesgado, junto con eta-cuadrado.
13.5 Comparaciones múltiples y pruebas post hoc
Cada vez que ejecutes un ANOVA con más de dos grupos y termines con un efecto significativo, lo primero que probablemente querrás preguntar es qué grupos son realmente diferentes entre sí. En nuestro ejemplo de fármacos, nuestra hipótesis nula fue que los tres fármacos (placebo, Anxifree y Joyzepam) tienen exactamente el mismo efecto sobre el estado de ánimo. Pero si lo piensas bien, la hipótesis nula en realidad afirma tres cosas diferentes a la vez aquí. En concreto, afirma que:
- El fármaco de tu competidor (Anxifree) no es mejor que un placebo (es decir, \(\mu_A = \mu_P\) )
- Tu fármaco (Joyzepam) no es mejor que un placebo (es decir, \(\mu_J = \mu_P\) )
- Anxifree y Joyzepam son igualmente efectivos (es decir, \(\mu_J = \mu_A\))
Si alguna de esas tres afirmaciones es falsa, entonces la hipótesis nula también es falsa. Entonces, ahora que hemos rechazado nuestra hipótesis nula, estamos pensando que al menos una de esas cosas no es cierta. ¿Pero cuál? Las tres proposiciones son de interés. Dado que deseas saber si tu nuevo fármaco Joyzepam es mejor que un placebo, sería bueno saber cómo actúa en relación a una alternativa comercial existente (es decir, Anxifree). Incluso sería útil comprobar el rendimiento de Anxifree frente al placebo. Incluso si Anxifree ya ha sido ampliamente probado contra placebos por otros investigadores, aún puede ser muy útil verificar que tu estudio esté produciendo resultados similares a trabajos anteriores.
Cuando caracterizamos la hipótesis nula en términos de estas tres proposiciones distintas, queda claro que hay ocho “estados del mundo” posibles entre los que debemos distinguir (Table 13.9).
| possibility: | is \( \mu_P = \mu_A \)? | is \( \mu_P = \mu_J \)? | is \( \mu_A = \mu_J \)? | which hypothesis? |
|---|---|---|---|---|
| 1 | \( \checkmark \) | \( \checkmark \) | \( \checkmark \) | null |
| 2 | \( \checkmark \) | \( \checkmark \) | alternative | |
| 3 | \( \checkmark \) | \( \checkmark \) | alternative | |
| 4 | \( \checkmark \) | alternative | ||
| 5 | \( \checkmark \) | \( \checkmark \) | \( \checkmark \) | alternative |
| 6 | \( \checkmark \) | alternative | ||
| 7 | \( \checkmark \) | alternative | ||
| 8 | alternative |
Al rechazar la hipótesis nula, hemos decidido que no creemos que el número 1 sea el verdadero estado del mundo. La siguiente pregunta es, ¿cuál de las otras siete posibilidades creemos que es correcta? Cuando te enfrentas a esta situación, por lo general ayuda mirar los datos. Por ejemplo, si observamos las gráficas en Figure 13.1, es tentador concluir que Joyzepam es mejor que el placebo y mejor que Anxifree, pero no hay una diferencia real entre Anxifree y el placebo. Sin embargo, si queremos obtener una respuesta más clara sobre esto, podría ser útil realizar algunas pruebas.
13.5.1 Ejecución de pruebas t “por pares”
¿Cómo podríamos solucionar nuestro problema? Dado que tenemos tres pares separados de medias (placebo versus Anxifree, placebo versus Joyzepam y Anxifree versus Joyzepam) para comparar, lo que podríamos hacer es ejecutar tres pruebas t separadas y ver qué sucede. Esto es fácil de hacer en jamovi. Puedes ir a las opciones de ANOVA ‘Pruebas post hoc’, mueve la variable ‘fármaco’ al cuadro activo de la derecha y luego haz clic en la casilla de verificación ‘Sin corrección’. Esto producirá una tabla ordenada que muestra todas las comparaciones de la prueba t por pares entre los tres niveles de la variable del fármaco, como en Figure 13.4

13.5.2 Correcciones para pruebas múltiples
En la sección anterior, insinué que hay un problema con ejecutar montones y montones de pruebas t. El problema es que, al ejecutar estos análisis, lo que estamos haciendo es una “expedición de pesca”. Estamos realizando montones de pruebas sin mucha orientación teórica con la esperanza de que algunas de ellas resulten significativas. Este tipo de búsqueda sin teoría de diferencias entre grupos se conoce como análisis post hoc (“post hoc” en latín significa “después de esto”).10
Está bien ejecutar análisis post hoc, pero hay que tener mucho cuidado. Por ejemplo, se debe evitar el análisis que realicé en la sección anterior, ya que cada prueba t individual está diseñada para tener una tasa de error Tipo I del 5 % (es decir, \(\alpha = .05\)) y realicé tres de estas pruebas. Imagina lo que hubiera pasado si mi ANOVA involucrara 10 grupos diferentes, y hubiera decidido ejecutar 45 pruebas t “post hoc” para tratar de averiguar cuáles eran significativamente diferentes entre sí, esperaría que 2 o 3 de ellas resultaran significativas solo por casualidad. Como vimos en Chapter 9, el principio organizador central que subyace a la prueba de hipótesis nula es que buscamos controlar nuestra tasa de error Tipo I, pero ahora que estoy ejecutando muchas pruebas t a la vez para determinar la fuente de mis resultados de ANOVA, mi tasa de error Tipo I real se ha salido completamente de control.
La solución habitual a este problema es introducir un ajuste en el valor p, cuyo objetivo es controlar la tasa de error total en toda la familia de pruebas (ver Shaffer (1995)). Un ajuste de esta forma, que generalmente (pero no siempre) se aplica porque una está haciendo un análisis post hoc, a menudo se denomina ** corrección para comparaciones múltiples **, aunque a veces se denomina “inferencia simultánea”. En cualquier caso, hay bastantes formas diferentes de hacer este ajuste. Discutiré algunas de ellas en esta sección y en Section 14.8 el próximo capítulo, pero debes tener en cuenta que existen muchos otros métodos (consulta, por ejemplo, Hsu (1996)).
13.5.3 Correcciones de Bonferroni
El más simple de estos ajustes se llama la corrección de Bonferroni (Dunn, 1961), y es muy, muy simple. Supongamos que mi análisis post hoc consta de m pruebas separadas, y quiero asegurarme de que la probabilidad total de cometer cualquier error de tipo I sea como máximo \(\alpha\).11 Si es así, entonces la corrección de Bonferroni simplemente dice “multiplique todos sus valores p sin procesar por m”. Si dejamos que \(p\) denote el valor p original y que \(p_j^{'}\) sea el valor corregido, entonces la corrección de Bonferroni dice que:
\[p_j^{'}=m \times p\]
Y por lo tanto, si usas la corrección de Bonferroni, rechazarías la hipótesis nula si \(p_j^{'} < \alpha\). La lógica de esta corrección es muy sencilla. Estamos haciendo m pruebas diferentes, por lo que si lo organizamos para que cada prueba tenga una tasa de error de tipo I de \(\frac{\alpha}{m}\) como máximo, entonces la tasa de error de tipo I total en estas pruebas no puede ser mayor que \(\alpha\). Eso es bastante simple, tanto que en el artículo original, el autor escribe:
El método dado aquí es tan simple y tan general que estoy seguro de que debe haber sido usado antes. Sin embargo, no lo encuentro, por lo que solo puedo concluir que quizás su misma simplicidad ha impedido que los estadísticos se den cuenta de que es un método muy bueno en algunas situaciones (Dunn (1961), pp 52-53).
Para usar la corrección de Bonferroni en jamovi, simplemente haz clic en la casilla de verificación ‘Bonferroni’ en las opciones de ‘Corrección’ y verás otra columna añadida a la tabla de resultados de ANOVA que muestra los valores p ajustados para la corrección de Bonferroni (Table 13.8). Si comparamos estos tres valores p con los de las pruebas t por pares sin corregir, está claro que lo único que ha hecho jamovi es multiplicarlos por \(3\).
13.5.4 Correcciones de Holm
Aunque la corrección de Bonferroni es el ajuste más simple que existe, no suele ser el mejor. Un método que se usa a menudo es la corrección de Holm (Holm, 1979). La idea detrás de la corrección de Holm es pretender que está haciendo las pruebas secuencialmente, comenzando con el valor p más pequeño (sin procesar) y avanzando hacia el más grande. Para el j-ésimo mayor de los valores p, el ajuste es cualquiera
\[p_j^{'}=j \times p_j\]
(es decir, el valor de p más grande permanece sin cambios, el segundo valor de p más grande se duplica, el tercer valor de p más grande se triplica, y así sucesivamente), o
\[p_j^{'}=p_{j+1}^{'}\]
el que sea más grande. Esto puede ser un poco confuso, así que hagámoslo un poco más despacio. Esto es lo que hace la corrección de Holm. Primero, ordena todos sus valores p en orden, de menor a mayor. Para el valor p más pequeño, todo lo que tiene que hacer es multiplicarlo por \(m\) y listo. Sin embargo, para todos los demás es un proceso de dos etapas. Por ejemplo, cuando pasa al segundo valor p más pequeño, primero lo multiplica por \(m - 1\). Si esto produce un número que es mayor que el valor p ajustado que obtuvo la última vez, entonces lo conserva. Pero si es más pequeño que el último, copia el último valor p. Para ilustrar cómo funciona esto, considera Table 13.10 que muestra los cálculos de una corrección de Holm para una colección de cinco valores p.
| raw p | rank j | p \( \times \) j | Holm p |
|---|---|---|---|
| .001 | 5 | .005 | .005 |
| .005 | 4 | .020 | .020 |
| .019 | 3 | .057 | .057 |
| .022 | 2 | .044 | .057 |
| .103 | 1 | .103 | .103 |
Esperemos que eso aclare las cosas.
Aunque es un poco más difícil de calcular, la corrección de Holm tiene algunas propiedades muy buenas. Es más potente que Bonferroni (es decir, tiene una tasa de error de tipo II más baja) pero, aunque parezca contradictorio, tiene la misma tasa de error tipo I. Como consecuencia, en la práctica casi nunca se utiliza la corrección de Bonferroni, ya que siempre es superada por la corrección de Holm, un poco más elaborada. Debido a esto, la corrección de Holm debería ser tu ir a corrección de comparación múltiple. Figure 13.4 también muestra los valores p corregidos de Holm y, como puedes ver, el valor p más grande (correspondiente a la comparación entre Anxifree y el placebo) no se modifica. Con un valor de .15, es exactamente el mismo que el valor que obtuvimos originalmente cuando no aplicamos ninguna corrección. Por el contrario, el valor de p más pequeño (Joyzepam frente a placebo) se ha multiplicado por tres.
13.5.5 Redacción de la prueba post hoc
Finalmente, después de ejecutar el análisis post hoc para determinar qué grupos son significativamente diferentes entre sí, puedes escribir el resultado de esta manera:
Las pruebas post hoc (usando la corrección de Holm para ajustar p) indicaron que Joyzepam produjo un cambio de humor significativamente mayor que Anxifree (p = .001) y el placebo (\((p = 9.0 \times{10^{-5} }\)). No encontramos evidencia de que Anxifree funcionara mejor que el placebo (\(p = .15\)).
O, si no te gusta la idea de informar valores p exactos, entonces cambiarías esos números por \(p < .01\), \(p < .001\) y \(p > .05\) respectivamente. De todas formas, la clave es que indiques que utilizaste la corrección de Holm para ajustar los valores p. Y, por supuesto, asumo que en otra parte del artículo has incluido los estadísticos descriptivos relevantes (es decir, las medias del grupo y las desviaciones estándar), ya que estos valores p por sí solos no son muy informativos.
13.6 Los supuestos de ANOVA unifactorial
Como cualquier prueba estadística, el análisis de varianza se basa en algunas suposiciones sobre los datos, específicamente los residuales. Hay tres suposiciones clave que debes tener en cuenta: normalidad, homogeneidad de varianzas e independencia.
[Detalle técnico adicional 12]
Entonces, ¿cómo verificamos si la suposición sobre los residuales es correcta? Bueno, como indiqué anteriormente, hay tres afirmaciones distintas subyacentes en esta declaración, y las consideraremos por separado.
- Homogeneidad de varianzas. Fíjate que solo tenemos un valor para la desviación estándar de la población (es decir, \(\sigma\)), en lugar de permitir que cada grupo tenga su propio valor (es decir, \(\sigma_k\)). Esto se conoce como el supuesto de homogeneidad de varianzas (a veces llamado homocedasticidad). ANOVA asume que la desviación estándar de la población es la misma para todos los grupos. Hablaremos de esto extensamente en la sección Comprobación del supuesto de homogeneidad de varianzas.
- Normalidad. Se supone que los residuales se distribuyen normalmente. Como vimos en Section 11.9, podemos evaluar esto mirando gráficos QQ (o ejecutando una prueba de Shapiro-Wilk). Hablaré más sobre esto en un contexto ANOVA en la sección Comprobación del supuesto de normalidad.
- Independencia. La suposición de independencia es un poco más complicada. Lo que básicamente significa es que conocer un residual no dice nada sobre ningún otro residual. Se supone que todos los valores de \(\epsilon_{ik}\) han sido generados sin ninguna “consideración” o “relación con” ninguno de los otros. No hay una manera obvia o simple de probar esto, pero hay algunas situaciones que son violaciones claras de esto. Por ejemplo, si tienes un diseño de medidas repetidas, donde cada participante en tu estudio aparece en más de una condición, entonces la independencia no se cumple. ¡Hay una relación especial entre algunas observaciones, a saber, aquellas que corresponden a la misma persona! Cuando eso sucede, debes usar un ANOVA unifactorial de medidas repetidas.
13.6.1 Comprobación del supuesto de homogeneidad de varianzas
¡Hacer la prueba preliminar de las varianzas es como hacerse a la mar en un bote de remos para averiguar si las condiciones son lo suficientemente tranquilas para que un trasatlántico salga del puerto!
– Caja de Jorge (Box, 1953)
Hay más de una manera de probar el supuesto de homogeneidad de varianzas. La prueba más utilizada para esto que he visto en la literatura es la prueba de Levene (Levene, 1960), y la prueba de Brown-Forsythe estrechamente relacionada (Brown & Forsythe, 1974).
Independientemente de si estás haciendo la prueba estándar de Levene o la prueba de Brown-Forsythe, la prueba estadística, que a veces se denota \(F\) pero también a veces se escribe como \(W\), se calcula exactamente de la misma manera que la F para el ANOVA, simplemente usando \(Z_{ik}\) en lugar de \(Y_{ik}\). Con eso en mente, podemos pasar a ver cómo ejecutar la prueba en jamovi.
[Detalle técnico adicional 13]
13.6.2 Ejecutando la prueba de Levene en jamovi
Bien, entonces, ¿cómo hacemos la prueba de Levene? Realmente simple: en la opción “Comprobaciones de supuestos” de ANOVA, simplemente haz clic en la casilla de verificación “Pruebas de homogeneidad”. Si observamos el resultado, que se muestra en Figure 13.5, vemos que la prueba no es significativa (\(F_{2,15} = 1.45, p = .266\)), por lo que parece que el supuesto de homogeneidad de varianzas está bien. Sin embargo, ¡las apariencias pueden engañar! Si el tamaño de tu muestra es bastante grande, entonces la prueba de Levene podría mostrar un efecto significativo (es decir, p < .05) incluso cuando el supuesto de homogeneidad varianzas no se viole hasta el punto de afectar la solidez de ANOVA. Este era el punto al que George Box se refería en la cita anterior. De manera similar, si el tamaño de tu muestra es bastante pequeño, es posible que no se satisfaga el supuesto de homogeneidad de varianzas y, sin embargo, una prueba de Levene podría no ser significativa (es decir, p > 0,05). Lo que esto significa es que, junto con cualquier prueba estadística del cumplimiento del supuesto, siempre debes trazar la desviación estándar alrededor de las medias para cada grupo/categoría en el análisis… solo para ver si son bastante similares (es decir, homogeneidad de varianzas) o no.

13.6.3 Eliminar el supuesto de homogeneidad de varianzas
En nuestro ejemplo, el supuesto de homogeneidad de varianzas resultó ser bastante seguro: la prueba de Levene resultó no significativa (a pesar de que también deberíamos mirar el gráfico de las desviaciones estándar), por lo que probablemente no tengamos que preocuparnos. Sin embargo, en la vida real no siempre somos tan afortunados. ¿Cómo realizamos nuestro ANOVA cuando se viola el supuesto de homogeneidad de varianzas? Si recuerdas nuestra discusión sobre las pruebas t, vimos este problema antes. La prueba t de Student asume varianzas iguales, por lo que la solución fue usar la prueba t de Welch, que no lo hace. De hecho, Welch (1951) también mostró cómo podemos resolver este problema para ANOVA (la prueba unifactorial de Welch). Se implementa en jamovi utilizando el análisis ANOVA unifactorial. Se trata de un enfoque de análisis específico solo para ANOVA unifactorial, y para ejecutar el ANOVA unifactorial de Welch para nuestro ejemplo, volveríamos a ejecutar el análisis como antes, pero esta vez usamos el comando de análisis jamovi ANOVA - ANOVA unifactorial, y marcas la opción para la prueba de Welch (ver Figure 13.6). Para comprender lo que está sucediendo aquí, comparemos estos números con lo que obtuvimos anteriormente cuando Ejecutando un ANOVA en jamovi originalmente. Para ahorrarte la molestia de retroceder, esto es lo que obtuvimos la última vez: \(F(2, 15) = 18,611, p = 0,00009\), que también se muestra como la prueba de Fisher en el ANOVA unifactorial que se muestra en Figure 13.6.
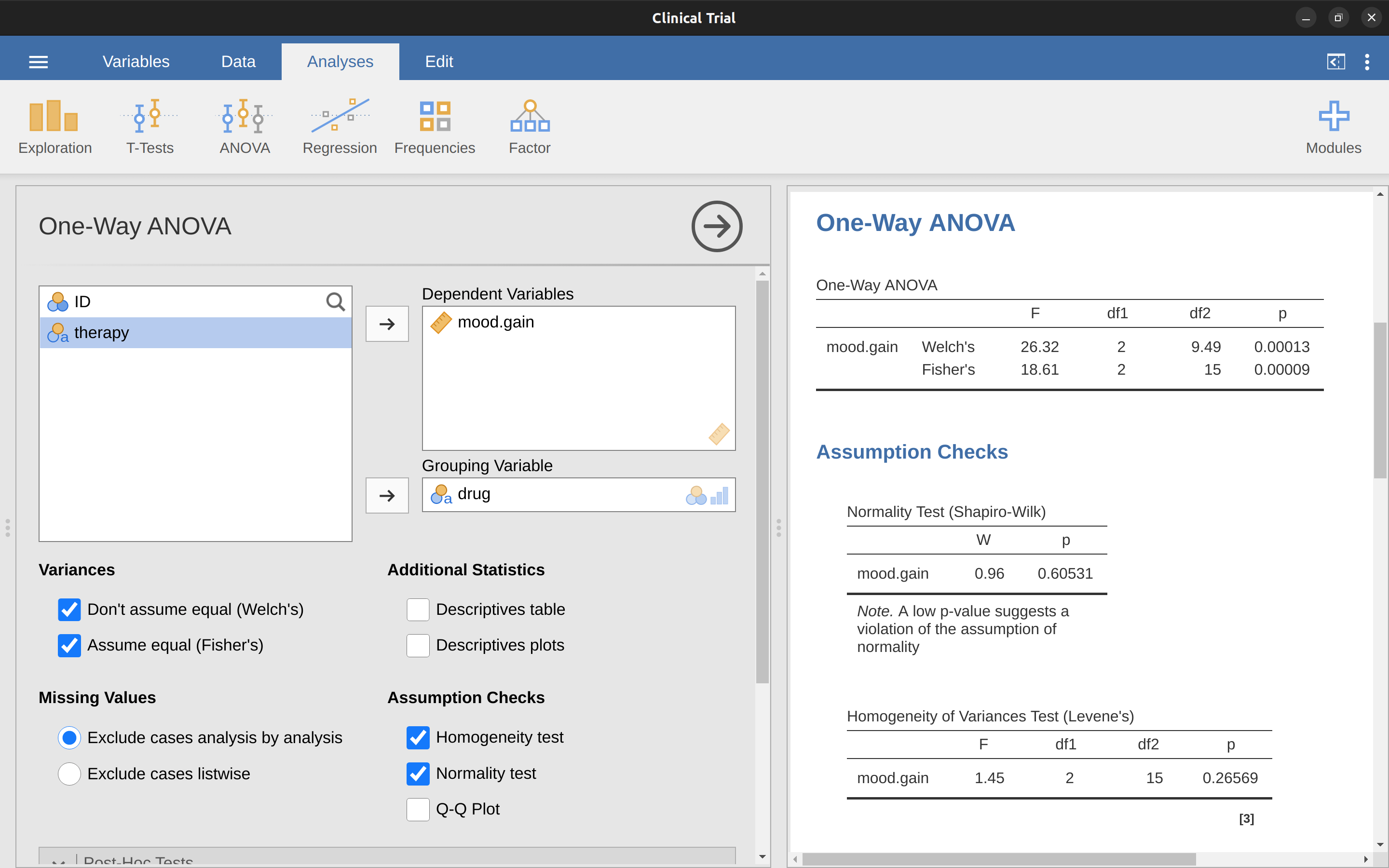
Bien, originalmente nuestro ANOVA nos dio el resultado \(F(2, 15) = 18,6\), mientras que la prueba unifactorial de Welch nos dio \(F(2, 9,49) = 26,32\). En otras palabras, la prueba de Welch ha reducido los grados de libertad dentro de los grupos de 15 a 9,49 y el valor F ha aumentado de 18,6 a 26,32.
13.6.4 Comprobación del supuesto de normalidad
Probar el supuesto de normalidad es relativamente sencillo. Cubrimos la mayor parte de lo que necesitas saber en Section 11.9. Lo único que realmente necesitamos hacer es dibujar un gráfico QQ y, además, si está disponible, ejecutar la prueba de Shapiro-Wilk. El gráfico QQ se muestra en Figure 13.7 y me parece bastante normal. Si la prueba de Shapiro-Wilk no es significativa (es decir, \(p > 0,05\)), esto indica que no se viola el supuesto de normalidad. Sin embargo, al igual que con la prueba de Levene, si el tamaño de la muestra es grande, una prueba significativa de Shapiro-Wilk puede ser de hecho un falso positivo, donde la suposición de normalidad no se viola en ningún sentido problemático sustantivo para el análisis. Y, del mismo modo, una muestra muy pequeña puede producir falsos negativos. Por eso es importante una inspección visual del gráfico QQ.
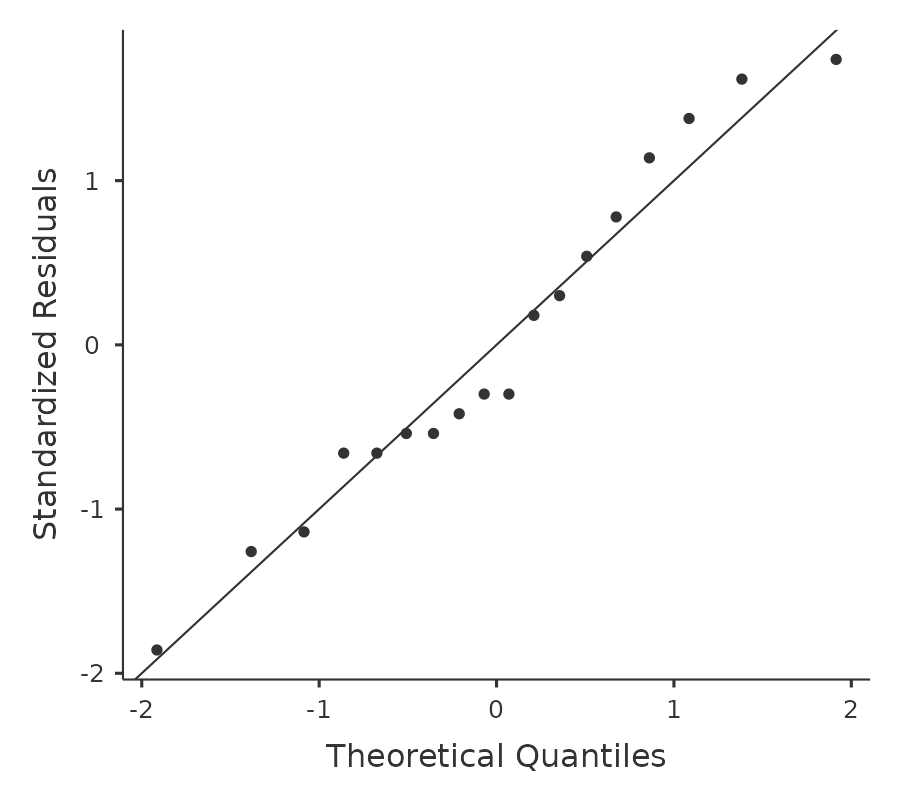
Además de inspeccionar el gráfico QQ en busca de desviaciones de la normalidad, la prueba de Shapiro-Wilk para nuestros datos muestra un efecto no significativo, con p = 0,6053 (ver Figure 13.6. Por lo tanto, esto respalda la evaluación del gráfico QQ; ambas comprobaciones no encuentran indicios de que se viole la normalidad.
13.6.5 Eliminando el supuesto de normalidad
Ahora que hemos visto cómo verificar la normalidad, nos preguntamos qué podemos hacer para abordar las violaciones de la normalidad. En el contexto de un ANOVA unifactorial, la solución más fácil probablemente sea cambiar a una prueba no paramétrica (es decir, una que no se base en ningún supuesto particular sobre el tipo de distribución involucrada). Hemos visto pruebas no paramétricas antes, en Chapter 11. Cuando solo tienes dos grupos, la prueba de Mann-Whitney o Wilcoxon proporciona la alternativa no paramétrica que necesitas. Cuando tengas tres o más grupos, puedes usar la prueba de suma de rangos de Kruskal-Wallis (Kruskal & Wallis, 1952). Esa es la prueba de la que hablaremos a continuación.
13.6.6 La lógica detrás de la prueba de Kruskal-Wallis
La prueba de Kruskal-Wallis es sorprendentemente similar a ANOVA, en algunos aspectos. En ANOVA comenzamos con \(Y_{ik}\), el valor de la variable de resultado para la i-ésima persona en el k-ésimo grupo. Para la prueba de Kruskal Wallis, lo que haremos es ordenar por rango todos estos valores de \(Y_{ik}\) y realizar nuestro análisis en los datos clasificados. 14
13.6.7 Detalles adicionales
La descripción en la sección anterior ilustra la lógica que subyace a la prueba de Kruskal-Wallis. A nivel conceptual, esta es la forma correcta de pensar en cómo funciona la prueba.15
¡Pero espera hay mas! La historia que he contado hasta ahora solo es cierta cuando no hay vínculos en los datos sin procesar. Es decir, si no hay dos observaciones que tengan exactamente el mismo valor. Si hay empates, entonces tenemos que introducir un factor de corrección a estos cálculos. En este punto, asumo que incluso el lector más diligente ha dejado de preocuparse (o al menos se ha formado la opinión de que el factor de corrección de empates es algo que no requiere su atención inmediata). Así que te diré muy rápidamente cómo se calcula y omitiré los tediosos detalles sobre por qué se hace de esta manera. Supongamos que construimos una tabla de frecuencias para los datos sin procesar y que fj sea el número de observaciones que tienen el j-ésimo valor único. Esto puede sonar un poco abstracto, así que aquí hay un ejemplo concreto de la tabla de frecuencias de mood.gain del conjunto de datos Clinicaltrials.csv (Table 13.11)
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 | 0.9 | 1.1 | 1.2 | 1.3 | 1.4 | 1.7 | 1.8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
Observando esta tabla, fíjate que la tercera entrada en la tabla de frecuencias tiene un valor de 2. Dado que esto corresponde a una ganancia de estado de ánimo de 0,3, esta tabla nos dice que el estado de ánimo de dos personas aumentó en 0,3. 16
Y entonces jamovi usa un factor de corrección por empates para calcular el estadístico de Kruskall-Wallis corregido por empates. Y por fin hemos terminado con la teoría de la prueba de Kruskal-Wallis. Estoy segura de que estáis aliviadas de que os haya curado de la ansiedad existencial que surge naturalmente cuando os dais cuenta de que no sabeis cómo calcular el factor de corrección por empates para la prueba de Kruskal-Wallis. ¿Verdad?
13.6.8 Cómo ejecutar la prueba Kruskal-Wallis en jamovi
A pesar del horror por el que hemos pasado al tratar de entender lo que realmente hace la prueba Kruskal Wallis, resulta que ejecutar la prueba es bastante sencillo, ya que jamovi tiene un análisis como parte del conjunto de análisis ANOVA llamado ‘No paramétrico’ - ‘ANOVA unifactorial (Kruskall-Wallis)’ La mayoría de las veces tendrás datos como el conjunto de datos clinictrial.csv, en el que tienes tu variable de resultado mood.gain y una variable de agrupación de fármacos. Si es así, puedes continuar y ejecutar el análisis en jamovi. Lo que esto nos da es un Kruskal-Wallis \(\chi^2 =12.076, df = 2, p = 0.00239\), como en Figure 13.8

13.7 ANOVA unifactorial de medidas repetidas
La prueba ANOVA unifactorial de medidas repetidas es un método estadístico para probar diferencias significativas entre tres o más grupos donde se utilizan los mismos participantes en cada grupo (o cada participante se empareja con participantes en otros grupos experimentales). Por esta razón, siempre debe haber un número igual de puntuaciones (datos) en cada grupo experimental. Este tipo de diseño y análisis también puede denominarse ‘ANOVA relacionado’ o ‘ANOVA intrasujeto’.
La lógica que subyace a un ANOVA de medidas repetidas es muy similar a la de un ANOVA independiente (a veces llamado ANOVA ‘entre sujetos’). Recordarás que anteriormente mostramos que en un ANOVA entre sujetos, la variabilidad total se divide en variabilidad entre grupos (\(SS_b\)) y variabilidad intra grupos (\(SS_w\)), y después de que cada uno se divide por los grados de libertad respectivos para dar MCe y MCi (ver Tabla 13.1) la F se calcula como:
\[F=\frac{MS_b}{MS_w}\]
En un ANOVA de medidas repetidas, la F se calcula de manera similar, pero mientras que en un ANOVA independiente la variabilidad dentro del grupo (\(SS_w\)) se usa como base para el denominador \(MS_w\), en un ANOVA de medidas repetidas el \(SS_w\) se divide en dos partes. Como estamos usando los mismos sujetos en cada grupo, podemos eliminar la variabilidad debida a las diferencias individuales entre los sujetos (referidos como SCsujetos) de la variabilidad dentro de los grupos. No entraremos en demasiados detalles técnicos sobre cómo se hace esto, pero esencialmente cada sujeto se convierte en un nivel de un factor llamado sujetos. La variabilidad en este factor intra-sujetos se calcula entonces de la misma manera que cualquier factor entre sujetos. Y luego podemos restar SCsujetos de \(SS_w\) para proporcionar un término de SCerror más pequeño:
\[\text{ANOVA independiente: } SS_{error} = SS_w\] \[\text{ANOVA de medidas repetidas: } SS_{error} = SS_w - SS_{sujetos}\] Este cambio en el término \(SS_{error}\) a menudo conduce a una prueba estadística más potente, pero esto depende de si la reducción en el \(SS_{error}\) compensa la reducción en los grados de libertad del término de error (a medida que los grados de libertad van de \((n - k)\) 17 a \((n - 1)(k - 1)\) (teniendo en cuenta que hay más sujetos en el diseño ANOVA independiente).
13.7.1 ANOVA de medidas repetidas en jamovi
Primero, necesitamos algunos datos. Geschwind (1972) ha sugerido que la naturaleza exacta del déficit de lenguaje de un paciente después de un accidente cerebrovascular se puede utilizar para diagnosticar la región específica del cerebro que se ha dañado. Una investigadora está interesada en identificar las dificultades de comunicación específicas experimentadas por seis pacientes que padecen afasia de Broca (un déficit del lenguaje comúnmente experimentado después de un accidente cerebrovascular) (Table 13.12).
| Participant | Speech | Conceptual | Syntax |
|---|---|---|---|
| 1 | 8 | 7 | 6 |
| 2 | 7 | 8 | 6 |
| 3 | 9 | 5 | 3 |
| 4 | 5 | 4 | 5 |
| 5 | 6 | 6 | 2 |
| 6 | 8 | 7 | 4 |
Los pacientes debían completar tres tareas de reconocimiento de palabras. En la primera tarea (producción del habla), los pacientes debían repetir palabras sueltas leídas en voz alta por la investigadora. En la segunda tarea (conceptual), diseñada para evaluar la comprensión de palabras, los pacientes debían relacionar una serie de imágenes con su nombre correcto. En la tercera tarea (sintaxis), diseñada para evaluar el conocimiento del orden correcto de las palabras, se pidió a los pacientes que reordenaran oraciones sintácticamente incorrectas. Cada paciente completó las tres tareas. El orden en que los pacientes realizaron las tareas fue contrabalanceado entre los participantes. Cada tarea consistió en una serie de 10 intentos. El número de intentos completados con éxito por cada paciente se muestra en Table 13.11. Introduce estos datos en jamovi listos para el análisis (o coge un atajo y carga el archivo broca.csv).
Para realizar un ANOVA relacionado unifactorial en jamovi, abre el cuadro de diálogo ANOVA de medidas repetidas unifactoriales, como en Figure 13.9, a través de ANOVA - ANOVA de medidas repetidas.
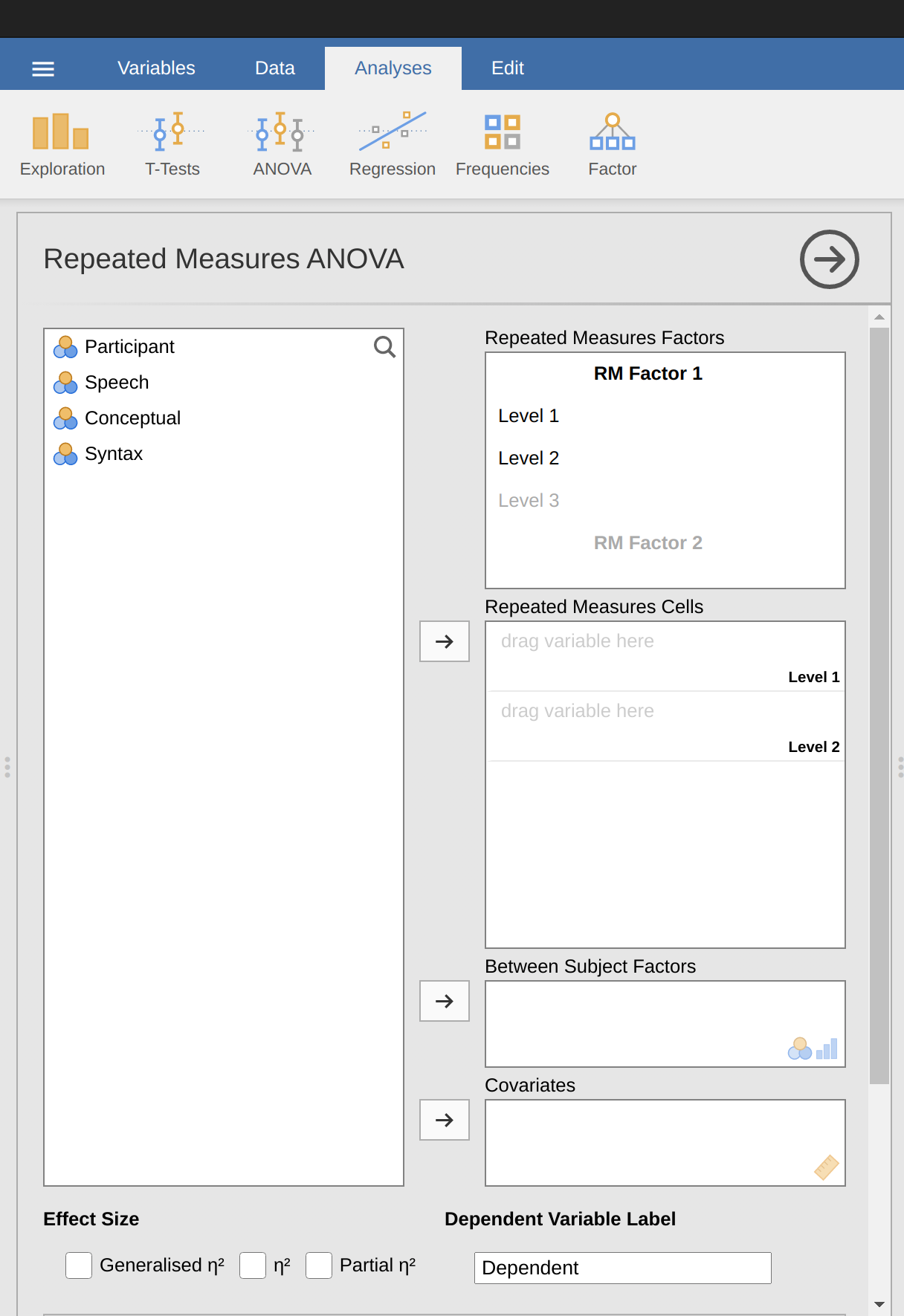
Después:
- Introduce un nombre de factor de medidas repetidas. Esta debe ser una etiqueta que elijas para describir las condiciones repetidas por todos los participantes. Por ejemplo, para describir las tareas de habla, conceptuales y sintácticas realizadas por todos los participantes, una etiqueta adecuada sería ‘Tarea’. Ten en cuenta que este nuevo nombre del factor representa la variable independiente en el análisis.
- Agrega un tercer nivel en el cuadro de texto Factores de medidas repetidas, ya que hay tres niveles que representan las tres tareas: discurso, conceptual y sintaxis. Cambia las etiquetas de los niveles respectivamente.
- Luego, mueve cada uno de los niveles de las variables al cuadro de texto de la celda de medidas repetidas.
- Finalmente, en la opción Comprobaciones de supuestos, marca el cuadro de texto “Comprobaciones de esfericidad”.
La salida jamovi para un ANOVA unifactorial de medidas repetidas se produce como se muestra en Figure 13.10 a Figure 13.13. El primer resultado que debemos observar es la prueba de esfericidad de Mauchly, que prueba la hipótesis de que las varianzas de las diferencias entre las condiciones son iguales (lo que significa que la dispersión de las puntuaciones de la diferencia entre las condiciones del estudio es aproximadamente la misma). En Figure 13.10, el nivel de significación de la prueba de Mauchly es \(p = .720\). Si la prueba de Mauchly no es significativa (es decir, p > 0,05, como es el caso en este análisis), entonces es razonable concluir que las varianzas de las diferencias no son significativamente diferentes (es decir, son aproximadamente iguales y se puede asumir la esfericidad).

Si por el contrario la prueba de Mauchly hubiera sido significativa (p < .05) entonces concluiríamos que existen diferencias significativas entre la varianza de las diferencias, y no se cumple el requisito de esfericidad. En este caso, deberíamos aplicar una corrección al valor F obtenido en el análisis ANOVA relacionado unifactorial:
- Si el valor de Greenhouse-Geisser en la tabla “Pruebas de esfericidad” es > 0,75, debes utilizar la corrección de Huynh-Feldt
- Pero si el valor de Greenhouse-Geisser es < .75, entonces debes usar la corrección de Greenhouse-Geisser.
Ambos valores F corregidos se pueden especificar en las casillas de verificación Correcciones de esfericidad en las opciones de Comprobaciones de supuestos, y los valores F corregidos se muestran luego en la tabla de resultados, como en la Figura 13.11.
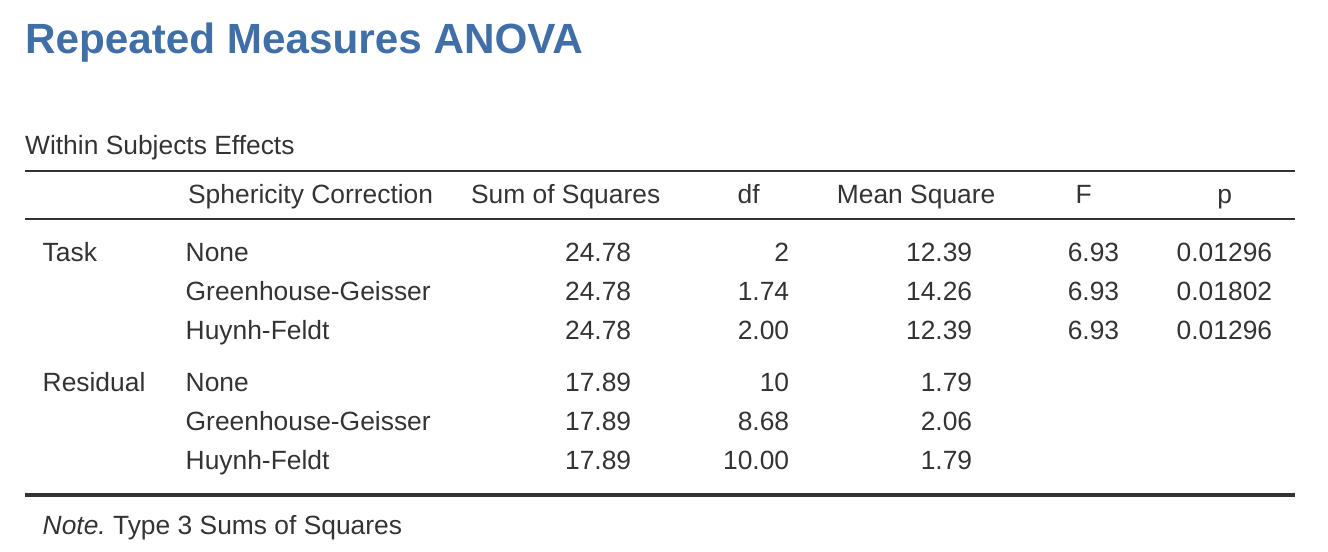
En nuestro análisis, vimos que la significación de la prueba de esfericidad de Mauchly fue p = .720 (es decir, p > 0.05). Por lo tanto, esto significa que podemos suponer que se ha cumplido el requisito de esfericidad, por lo que no es necesario corregir el valor F. Por lo tanto, podemos usar los valores de la corrección de esfericidad ‘Ninguno’ para la medida repetida ‘Tarea’: \(F = 6.93\), \(df = 2\), \(p = .013\), y podemos concluir que el número de pruebas exitosas completado en cada tarea de lenguaje varió significativamente dependiendo de si la tarea se basaba en el habla, la comprensión o la sintaxis (\(F(2, 10) = 6.93\), \(p = .013\)).
Las pruebas post-hoc también se pueden especificar en jamovi para ANOVA de medidas repetidas de la misma manera que para ANOVA independiente. Los resultados se muestran en Figure 13.12. Estos indican que existe una diferencia significativa entre Habla y Sintaxis, pero no entre otros niveles.
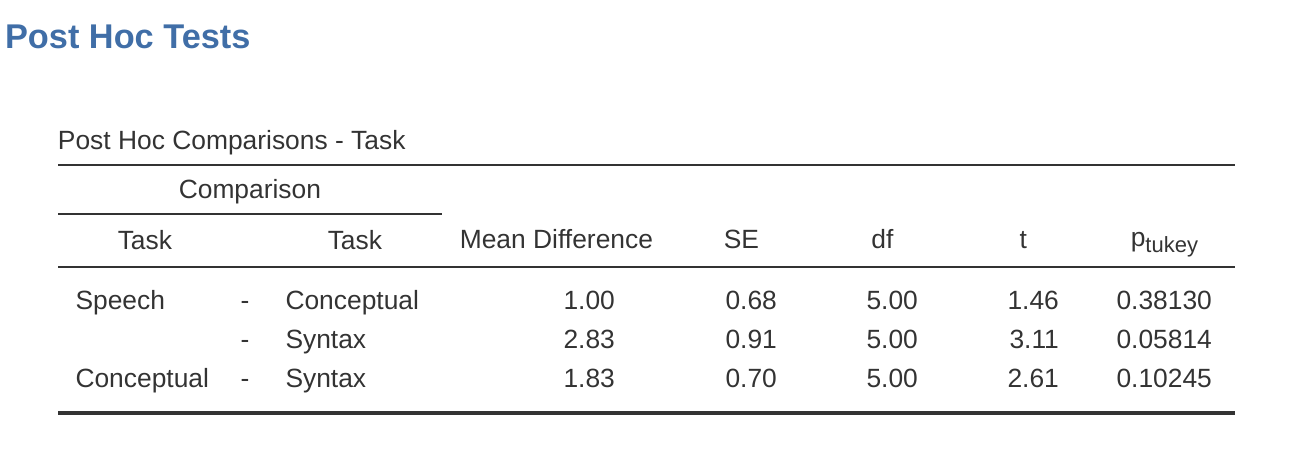
Los estadísticos descriptivos (medias marginales) se pueden revisar para ayudar a interpretar los resultados, producidos en la salida jamovi como en Figure 13.13. La comparación del número medio de intentos completados con éxito por los participantes muestra que las personas con afasia de Broca se desempeñan razonablemente bien en las tareas de producción del habla (media = 7,17) y comprensión del lenguaje (media = 6,17). Sin embargo, su desempeño fue considerablemente peor en la tarea de sintaxis (media = 4.33), con una diferencia significativa en las pruebas post-hoc entre el desempeño de la tarea de habla y sintaxis.

13.8 La prueba ANOVA no paramétrica de medidas repetidas de Friedman
La prueba de Friedman es una versión no paramétrica de un ANOVA de medidas repetidas y se puede usar en lugar de la prueba de Kruskall-Wallis cuando se prueban las diferencias entre tres o más grupos en los que los mismos participantes están en cada grupo, o cada participante está emparejado con participantes en otras condiciones. Si la variable dependiente es ordinal, o si no se cumple el supuesto de normalidad, se puede utilizar la prueba de Friedman.
Al igual que con la prueba de Kruskall-Wallis, las matemáticas subyacentes son complicadas y no se presentarán aquí. A los fines de este libro, es suficiente señalar que jamovi calcula la versión con corrección de empates de la prueba de Friedman, y en Figure 13.14 hay un ejemplo que usa los datos de Afasia de Broca que ya hemos visto.
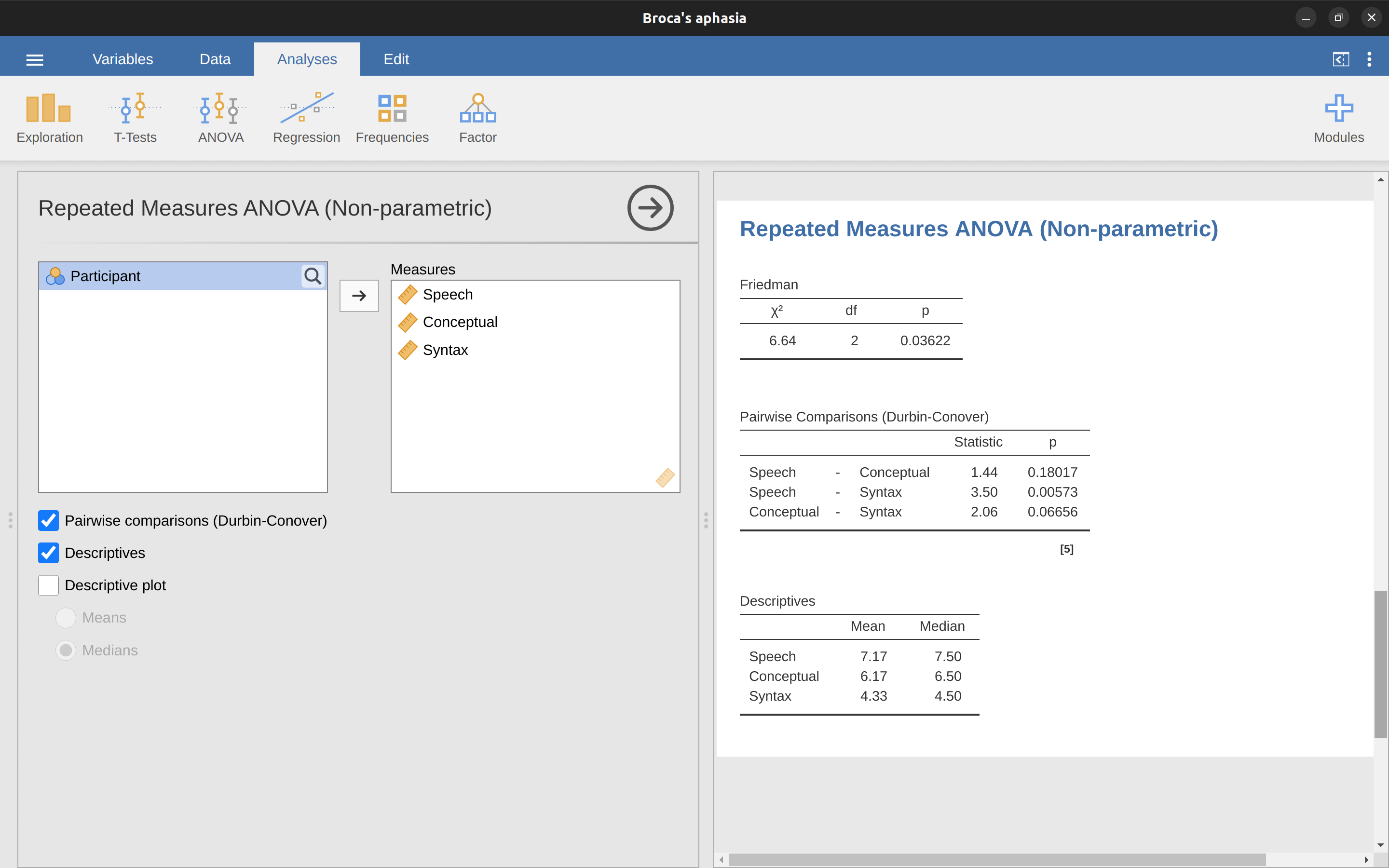
Es bastante sencillo ejecutar una prueba de Friedman en jamovi. Simplemente selecciona Análisis - ANOVA - ANOVA de medidas repetidas (no paramétrico), como en Figure 13.14. Luego resalta y transfiere los nombres de las variables de medidas repetidas que deseas comparar (Habla, Conceptual, Sintaxis) al cuadro de texto ‘Medidas:’. Para producir estadísticos descriptivos (medias y medianas) para las tres variables de medidas repetidas, haz clic en el botón Descriptivos.
Los resultados de jamovi muestran los estadísticos descriptivos, el valor de ji-cuadrado, los grados de libertad y el valor p (Figure 13.14). Dado que el valor p es menor que el nivel utilizado convencionalmente para determinar la importancia (p < 0,05), podemos concluir que los afásicos de Broca se desempeñan razonablemente bien en las tareas de producción del habla (mediana = 7,5) y comprensión del lenguaje (mediana = 6,5). Sin embargo, su desempeño fue considerablemente peor en la tarea de sintaxis (mediana = 4.5), con una diferencia significativa en las pruebas post-hoc entre el desempeño de la tarea de Habla y Sintaxis.
13.9 Sobre la relación entre ANOVA y la prueba t de Student
Hay una última cosa que quiero señalar antes de terminar. Es algo que mucha gente encuentra un poco sorprendente, pero vale la pena conocerlo. Un ANOVA con dos grupos es idéntico a la prueba t de Student. No es solo que sean similares, sino que en realidad son equivalentes en todos los aspectos relevantes. No intentaré demostrar que esto es cierto, pero os haré una sola demostración concreta. Supongamos que, en lugar de ejecutar un ANOVA en nuestro modelo de fármacos mood.gain ~, lo hacemos usando la terapia como predictor. Si ejecutamos este ANOVA obtenemos un estadístico F de \(F(1,16) = 1,71\) y un valor p = \(0,21\). Dado que solo tenemos dos grupos, en realidad no necesitábamos recurrir a un ANOVA, podríamos haber decidido ejecutar una prueba t de Student. Veamos qué sucede cuando hacemos esto: obtenemos un estadístico t de \(t(16) = -1.3068\) y un valor de \(p = 0.21\). Curiosamente, los valores de p son idénticos. Nuevamente obtenemos un valor de \(p = .21\). Pero, ¿qué pasa con la prueba estadística? Después de ejecutar una prueba t en lugar de un ANOVA, obtenemos una respuesta algo diferente, a saber, \(t(16) = -1,3068\). Sin embargo, la relación es bastante sencilla. Si elevamos al cuadrado el estadístico t, obtenemos el estadístico F de antes: \(-1.3068^{2} = 1.7077\)
13.10 Resumen
Hemos tratado bastante en este capítulo, pero aún falta mucho 18. Obviamente, no he discutido cómo ejecutar un ANOVA cuando nos interesa más de una variable de agrupación, pero eso se discutirá con mucho detalle en Chapter 14. En términos de lo que hemos discutido, los temas clave fueron:
- La lógica básica que subyace a Cómo funciona ANOVA y [Ejecutar un ANOVA en jamovi]
- Cómo calcular un Tamaño del efecto para un ANOVA.
- Comparaciones múltiples y pruebas post hoc para pruebas múltiples.
- Los supuestos de ANOVA unifactorial
- [Comprobación del supuesto de homogeneidad de varianza] y qué hacer si se infringe: [Eliminación del supuesto de homogeneidad de varianza]
- Comprobación del supuesto de normalidad y qué hacer si se infringe: [Eliminación del supuesto de normalidad]
- ANOVA unifactorial de medidas repetidas y el equivalente no paramétrico, La prueba ANOVA no paramétrica de medidas repetidas de Friedman
cuando todos los grupos tienen el mismo número de observaciones, se dice que el diseño experimental está “equilibrado”. El equilibrio no es un gran problema para ANOVA unifactorial, que es el tema de este capítulo. Es más importante cuando haces ANOVA más complicados.↩︎
Por lo tanto, la fórmula para la suma de cuadrados total es casi idéntica a la fórmula para la varianza \[SS_{tot}=\sum_{k=1 }^{G} \sum_{i=1}^{N_k} (Y_{ik} - \bar{Y})^2\]↩︎
Una cosa muy positiva acerca de la suma de cuadrados total es que podemos dividirla en dos tipos diferentes de variación. Primero, podemos hablar de la suma de cuadrados intragrupo, en la que buscamos ver qué tan diferente es cada persona individual de su propia media de grupo \[SS_{w}= \sum_{k=1}^{G} \sum_{i=1}^{ N_k} (Y_{ik} - \bar{Y}_k)^2\] donde \(\bar{Y}_k\) es la media del grupo. En nuestro ejemplo, \(\bar{Y}_k\) sería el cambio de estado de ánimo promedio experimentado por aquellas personas que recibieron el k-ésimo fármaco. Así, en lugar de comparar individuos con el promedio de todas las personas en el experimento, solo los estamos comparando con aquellas personas del mismo grupo. Como consecuencia, esperaríamos que el valor de \(SS_w\) fuera menor que la suma de cuadrados total, porque ignora por completo las diferencias de grupo, es decir, si los fármacos tendrán efectos diferentes en el estado de ánimo de las personas.↩︎
para cuantificar el alcance de esta variación, lo que hacemos es calcular la suma de cuadrados entre grupos \[ \begin{aligned} SS_{ b} &= \sum_{k=1}^{G} \sum_{i=1}^{N_k} ( \bar{Y}_{k} - \bar{Y} )^2 \\ &= \ sum_{k=1}^{G} N_k ( \bar{Y}_{k} - \bar{Y} )^2 \end{aligned} \]↩︎
SS_w también se conoce en un ANOVA independiente como la varianza del error, o \(SS_{error}\)↩︎
En un nivel básico, ANOVA es una competición entre dos modelos estadísticos diferentes, \(H_0\) y \(H_1\). Cuando describí las hipótesis nula y alternativa al comienzo de la sección, fui un poco imprecisa acerca de cuáles son realmente estos modelos. Arreglaré eso ahora, aunque probablemente no te agradaré por hacerlo. Si recuerdas, nuestra hipótesis nula era que todas las medias de los grupos son idénticas entre sí. Si es así, entonces una forma natural de pensar en la variable de resultado \(Y_{ik}\) es describir las puntuaciones individuales en términos de una sola media poblacional µ, más la desviación de esa media poblacional. Esta desviación generalmente se denota \(\epsilon_{ik}\) y tradicionalmente se le llama el error o residual asociado con esa observación. PEro ten cuidado. Tal como vimos con la palabra “significativo”, la palabra “error” tiene un significado técnico en estadística que no es exactamente igual a su definición cotidiana en español. En el lenguaje cotidiano, “error” implica un error de algún tipo, pero en estadística no (o al menos, no necesariamente). Con eso en mente, la palabra “residual” es un término mejor que la palabra “error”. En estadística, ambas palabras significan “variabilidad sobrante”, es decir, “cosas” que el modelo no puede explicar. En cualquier caso, así es como se ve la hipótesis nula cuando la escribimos como un modelo estadístico \[Y_{ik}=\mu+\epsilon_{ik}\] donde asumimos (discutido más adelante) que los valores residuales \(\epsilon_{ik}\) se distribuyen normalmente, con media \(0\) y una desviación estándar \(\sigma\) que es igual para todos los grupos. Para usar la notación que presentamos en Chapter 7, escribiríamos esta suposición así \[\epsilon_{ik} \sum Normal(0,\sigma^2)\] ¿Qué pasa con la hipótesis alternativa, \(H_1\)? ? La única diferencia entre la hipótesis nula y la hipótesis alternativa es que permitimos que cada grupo tenga una media poblacional diferente. Así, si dejamos que \(\mu_k\) denote la media de la población para el k-ésimo grupo en nuestro experimento, entonces el modelo estadístico correspondiente a \(H_1\) es \[Y_{ik}=\mu_k+\epsilon_{ik}\] donde, una vez más, asumimos que los términos de error se distribuyen normalmente con media 0 y desviación estándar \(\sigma\). Es decir, la hipótesis alternativa también asume que \(\epsilon \sim Normal(0,\sigma^2)\) Bueno, una vez que hemos descrito los modelos estadísticos que sustentan \(H_0\) y \(H_1\) con más detalle, ahora es bastante sencillo decir qué miden los valores de las medias cuadráticas y qué significa esto para la interpretación de \(F\). No te aburriré con la justificación de esto, pero resulta que la media cuadrática intra grupos, \(MS_w\), puede verse como un estimador de la varianza del error \(\sigma^2\) . La media cuadrática entre grupos \(MS_b\) también es un estimador, pero lo que estima es la varianza del error más una cantidad que depende de las verdaderas diferencias entre las medias de los grupos. Si llamamos a esta cantidad \(Q\), podemos ver que el estadístico F es básicamente \(^a\) \[F=\frac{\hat{Q}+\hat{\sigma}^2}{\hat{ \sigma}^2}\] donde el valor verdadero \(Q = 0\) si la hipótesis nula es verdadera, y Q < 0 si la hipótesis alternativa es verdadera (p. ej., Hays (1994), cap. 10). Por lo tanto, como mínimo, el valor \(F\) debe ser mayor que 1 para tener alguna posibilidad de rechazar la hipótesis nula. Ten en cuenta que esto no significa que sea imposible obtener un valor F menor que 1. Lo que significa es que si la hipótesis nula es verdadera, la distribución muestral de la razón F tiene una media de 1,[^b] por lo que necesitamos ver valores F mayores que 1 para rechazar con seguridad el valor nulo. Para ser un poco más precisas sobre la distribución muestral, observa que si la hipótesis nula es verdadera, tanto la media cuadrática entre grupos como la media cuadrática intra grupos son estimadores de la varianza de los residuales \(\epsilon_{ik}\). Si esos residuales se distribuyen normalmente, entonces podrías sospechar que la estimación de la varianza de \(\epsilon_{ik}\) tiene una distribución de ji cuadrado, porque (como se discutió en Section 7.6) eso es lo que la distribución ji cuadrado es: lo que obtienes cuando elevas al cuadrado un montón de cosas normalmente distribuidas y las sumas. Y dado que la distribución F es (nuevamente, por definición) lo que obtienes cuando calculas la relación entre dos cosas que están distribuidas en \(\chi^2\), tenemos nuestra distribución muestral. Obviamente, estoy pasando por alto un montón de cosas cuando digo esto, pero en términos generales, de aquí es de donde proviene nuestra distribución muestral.
—
\(^a\) Si sigues leyendo Chapter 14 y observas cómo se define el “efecto de tratamiento” en el nivel k de un factor en términos de $_k $ (ver sección sobre ANOVA factorial 2: diseños balanceados, interacciones permitidas]), resulta que \(Q\) se refiere a una media ponderada de los efectos del tratamiento al cuadrado, \(Q = \frac{(\sum_{k=1} ^{G}N_k \alpha_k^2)}{(G-1)}\)
\(^b\) O, si queremos ser rigurosos con la precisión, \(1+ \frac{2}{df_2-2}\)↩︎O, para ser precisas, imagina que “es 1899 y no tenemos amigos y nada mejor que hacer con nuestro tiempo que hacer algunos cálculos que no habría tenido ningún sentido en 1899 porque ANOVA no existió hasta alrededor de la década de 1920”.↩︎
En el ensayo clínico de Excel anova.xls, el valor de SCb resultó ser ligeramente diferente, \(3,45\), que el que se muestra en el texto anterior (¡redondeando errores!)↩︎
los resultados de jamovi son más precisos que los del texto anterior, debido a errores de redondeo.↩︎
si tienes alguna base teórica para querer investigar algunas comparaciones pero no otras, la historia es diferente. En esas circunstancias, en realidad no estás ejecutando análisis “post hoc” en absoluto, estás haciendo “comparaciones planificadas”. Hablo de esta situación más adelante en el libro: Section 14.9, pero por ahora quiero mantener las cosas simples.↩︎
vale la pena señalar de paso que no todos los métodos de ajuste intentan hacer esto. Lo que he descrito aquí es un enfoque para controlar lo que se conoce como “Family-wise Type I error rate”. Sin embargo, existen otras pruebas post hoc que buscan controlar la “tasa de descubrimiento falso”, que es algo diferente.↩︎
si recuerdas [Un ejemplo práctico], que espero que al menos hayas leído por encima incluso si no lo leíste todo, describí los modelos estadísticos que sustentan ANOVA de esta manera: \[H_0:Y_{ik}=\mu + \epsilon_{ik}\] \[H_1:Y_{ik}=\mu_k + \epsilon_{ik}\] En estas ecuaciones \(\mu\) se refiere a una única media general poblacional que es la misma para todos los grupos, y µk es la media poblacional del k-ésimo grupo. Hasta este punto, nos ha interesado principalmente si nuestros datos se describen mejor en términos de una media general única (la hipótesis nula) o en términos de diferentes medias específicas de grupo (la hipótesis alternativa). ¡Esto tiene sentido, por supuesto, ya que esa es en realidad la pregunta de investigación importante! Sin embargo, todos nuestros procedimientos de prueba se han basado implícitamente en una suposición específica sobre los residuales, \(\epsilon\_{ik}\), a saber, que \[\epsilon_{ik} \sum Normal(0,\sigma^2) \] Ningún procedimiento matemático funciona correctamente sin esta suposición. O, para ser precisos, puedes hacer todos los cálculos y terminarás con un estadístico F, pero no tienes ninguna garantía de que esta F realmente mida lo que crees que está midiendo, por lo que cualquier conclusión que puedas sacar en base a la prueba F podría ser incorrecta.↩︎
la prueba de Levene es sorprendentemente simple. Supongamos que tenemos nuestra variable de resultado \(Y_{ik}\). Todo lo que hacemos es definir una nueva variable, que llamaré \(Z_{ik}\), correspondiente a la desviación absoluta de la media del grupo \[Z_{ik}=Y_{ik}-\bar{Y}_{k }\] Vale, ¿de qué nos sirve esto? Bueno, pensemos un momento qué es realmente \(Z_{ik}\) y qué estamos tratando de probar. El valor de \(Z_{ik}\) es una medida de cómo la \(i\)-ésima observación en el \(k\)-ésimo grupo se desvía de la media de su grupo. Y nuestra hipótesis nula es que todos los grupos tienen la misma varianza, es decir, ¡las mismas desviaciones generales de las medias del grupo! Entonces, la hipótesis nula en una prueba de Levene es que las medias poblacionales de \(Z\) son idénticas para todos los grupos. Mmm. Entonces, lo que necesitamos ahora es una prueba estadística de la hipótesis nula de que todas las medias de los grupos son ìguales. ¿Donde hemos visto eso antes? Ah, claro, eso es ANOVA, y todo lo que hace la prueba de Levene es ejecutar un ANOVA en la nueva variable \(Z_{ik}\). ¿Qué pasa con la prueba de Brown-Forsythe? ¿Hace algo particularmente diferente? No. El único cambio con respecto a la prueba de Levene es que construye la variable transformada Z de una manera ligeramente diferente, utilizando desviaciones respecto a las medianas del grupo en lugar de desviaciones respecto a las medias del grupo. Es decir, para la prueba de Brown-Forsythe: \[Z_{ik}=Y_{ik}-median_k(Y)\] donde \(median_k(Y)\) es la mediana del grupo k.↩︎
Dejemos que R_{ik} se refiera a la clasificación otorgada al i-ésimo miembro del k-ésimo grupo. Ahora, calculemos \(\bar{R}_k\), el rango promedio dado a las observaciones en el grupo k-ésimo \[\bar{R}_k=\frac{1}{N_k}\sum_i R_{ik}\] y también calcula \(\bar{R}\), el rango medio general \[\bar{R}=\frac{1}{N}\sum_i\sum_k R_{ik}\] Ahora que hemos hecho esto, podemos calcular las desviaciones al cuadrado del rango medio general \(\bar{R}\). Cuando hacemos esto para las puntuaciones individuales, es decir, si calculamos \((R_{ik} - \bar{R})^2\) , lo que tenemos es una medida “no paramétrica” de cuánto se desvía la ik-ésima observación del rango medio general . Cuando calculamos la desviación al cuadrado de las medias del grupo de las medias generales, es decir, si calculamos \((R_{ik} - \bar{R})^2\), entonces lo que tenemos es una medida no paramétrica de cuánto el grupo se desvía del rango medio general. Con esto en mente, seguiremos la misma lógica que hicimos con ANOVA y definiremos nuestras medidas de sumas de cuadrados ordenadas, como lo hicimos antes. Primero, tenemos nuestras “sumas de cuadrados totales ordenadas” \[RSS_{tot}=\sum_k\sum_i (R_{ik}-\bar{R})^2\] y podemos definir las “sumas de cuadrados ordenadas entre grupos” como este \[\begin{aligned} RSS_{b}& =\sum{k}\sum_{i}(\bar{R}_{k}-\bar{R})^2 \\ &= \sum_{k} N_k (\bar{R}_{k}-\bar{R})^2 \end{aligned}\] Entonces, si la hipótesis nula es verdadera y no hay ninguna diferencia verdadera entre los grupos, esperarías que las sumas ordenadas entre grupos \(RSS_b\) fueran muy pequeñas, mucho más pequeñas que las sumas ordenadas totales \(RSS_{tot}\). Cualitativamente, esto es muy similar a lo que encontramos cuando construimos el estadístico F de ANOVA, pero por razones técnicas, el estadístico de Kruskal-Wallis, generalmente denominado K, se construye de una manera ligeramente diferente, \[K=( N-1) \times \frac{RSS_b}{RSS_{tot}}\] y si la hipótesis nula es verdadera, entonces la distribución muestral de K es aproximadamente ji cuadrada con \(G-1\) grados de libertad (donde $G $ es el número de grupos). Cuanto mayor sea el valor de K, menos consistentes serán los datos con la hipótesis nula, por lo que esta es una prueba unilateral. Rechazamos \(H_0\) cuando K es suficientemente grande.↩︎
Sin embargo, desde una perspectiva puramente matemática es innecesariamente complicado. No te mostraré la derivación, pero puedes usar un poco de ingenio algebraicos\(^b\) para ver que la ecuación para K puede ser \[K=\frac{12}{N(N-1)} \sum_k N_k \bar{R}_k^2 -3(N+1)\] Es esta última ecuación la que a veces ves para K. Es mucho más fácil de calcular que la versión que describí en la sección anterior, pero es solo que no tiene sentido para los humanos reales. Probablemente sea mejor pensar en K como lo describí anteriormente, como un análogo de ANOVA basado en rangos. Pero ten en cuenta que la prueba estadística que se calcula termina con un aspecto bastante diferente al que usamos para nuestro ANOVA original.
—
\(b\) Un término técnico↩︎Más concretamente, en la notación matemática que introduje anteriormente, esto nos dice que \(f_3 = 2\). Hurra. Entonces, ahora que sabemos esto, el factor de corrección por empates (FCE) es: \[TCF=1-\frac{\sum_j f_j^3 - f_j}{N^3 - N}\] El valor del estadístico de Kruskal-Wallis corregido por empates se obtiene dividiendo el valor de K por esta cantidad. Es esta versión corregida por empates la que calcula jamovi.↩︎
(n - k) : (número de sujetos - número de grupos)↩︎
Al igual que con todos los capítulos de este libro, me he basado en fuentes diferentes, pero el texto destacado que más me ha influido Sahai & Ageel (2000). No es un libro para principiantes, pero es un libro excelente para lectores más avanzados con interés en comprender las matemáticas que subyacen a ANOVA.↩︎