| number of flips | number of heads | proportion |
|---|---|---|
| 1 | 0 | 0.00 |
| 2 | 1 | 0.50 |
| 3 | 2 | 0.67 |
| 4 | 3 | 0.75 |
| 5 | 4 | 0.80 |
| 6 | 4 | 0.67 |
| 7 | 4 | 0.57 |
| 8 | 5 | 0.63 |
| 9 | 6 | 0.67 |
| 10 | 7 | 0.70 |
| 11 | 8 | 0.73 |
| 12 | 8 | 0.67 |
| 13 | 9 | 0.69 |
| 14 | 10 | 0.71 |
| 15 | 10 | 0.67 |
| 16 | 10 | 0.63 |
| 17 | 10 | 0.59 |
| 18 | 10 | 0.56 |
| 19 | 10 | 0.53 |
| 20 | 11 | 0.55 |
7 Introducción a la probabilidad
[Dios] nos ha concedido sólo el crepúsculo… de la Probabilidad.
– John Locke
Hasta este punto del libro, hemos tratado algunas de las ideas clave del diseño experimental y hemos hablado un poco de cómo resumir un conjunto de datos. Para mucha gente, esto es todo lo que hay en estadística: recopilar todos los números, calcular las medias, hacer dibujos y ponerlos en un informe en algún sitio. Es como coleccionar sellos pero con números. Sin embargo, la estadística abarca mucho más que eso. De hecho, la estadística descriptiva es una de las partes más pequeñas de la estadística y una de las menos potentes. La parte más importante y útil de la estadística es que proporciona información que permite hacer inferencias sobre los datos.
Una vez que empiezas a pensar en la estadística en estos términos, que la estadística está ahí para ayudarnos a sacar conclusiones de los datos, empiezas a ver ejemplos de ello en todas partes. Por ejemplo, aquí hay un pequeño extracto de un artículo de periódico del Sydney Morning Herald (30 de octubre de 2010):
“Tengo un trabajo difícil”, dijo la Primera Ministra en respuesta a una encuesta que reveló que su gobierno es ahora la administración laborista más impopular de la historia, con un voto en las primarias de solo el 23 por ciento.
Este tipo de comentario es totalmente anodino en los periódicos o en la vida cotidiana, pero pensemos en lo que implica. Una empresa de sondeos ha realizado una encuesta, por lo general bastante grande porque se lo puede permitir. Me da pereza buscar la encuesta original, así que imaginemos que han llamado al azar a 1000 votantes de New South Wales (NSW), y 230 (23%) de ellos afirman que tienen la intención de votar por el Partido Laborista Australiano (ALP). En las elecciones federales de 2010, la Comisión Electoral Australiana informó de 4.610.795 votantes inscritos en NSW, por lo que desconocemos las opiniones de los 4.609.795 votantes restantes (alrededor del 99,98 % de los votantes). Incluso suponiendo que nadie mintiera a la empresa encuestadora, lo único que podemos afirmar con un 100 % de seguridad es que el verdadero voto del ALP en las primarias se sitúa entre 230/4610795 (alrededor del 0,005%) y 4610025/4610795 (alrededor del 99,83%). Entonces, ¿en qué se basan la empresa de encuestas, el periódico y los lectores para llegar a la conclusión de que el voto primario del ALP es solo del 23%?
La respuesta a la pregunta es bastante obvia. Si llamo a 1000 personas al azar y 230 de ellas dicen que tienen intención de votar al ALP, parece muy poco probable que estas sean las únicas 230 personas de todo el público votante que realmente tienen la intención de votar por ALP. En otras palabras, asumimos que los datos recopilados por la empresa encuestadora son bastante representativos de la población en general. Pero, ¿hasta qué punto? ¿Nos sorprendería descubrir que el verdadero voto ALP en las primarias es en realidad el 24%? 29%? 37%? En este punto, la intuición cotidiana empieza a fallar un poco. Nadie se sorprendería del 24 % y todo el mundo se sorprendería del 37 %, pero es un poco difícil decir si el 29 % es plausible. Necesitamos herramientas más potentes que mirar los números y adivinar.
La estadística inferencial nos proporciona las herramientas que necesitamos para responder este a tipo de preguntas y, dado que este tipo de preguntas constituyen el núcleo de la empresa científica, ocupan la mayor parte de los cursos introductorios sobre estadística y métodos de investigación. Sin embargo, la teoría de la inferencia estadística se basa en la teoría de la probabilidad. Y es a la teoría de la probabilidad a la que debemos referirnos ahora. Esta discusión de la teoría de la probabilidad es básicamente un detalle de fondo. No hay mucha estadística en sí en este capítulo, y no es necesario comprender este material con tanta profundidad como los otros capítulos de esta parte del libro. Sin embargo, dado que la teoría de la probabilidad sustenta gran parte de la estadística, merece la pena cubrir algunos de los aspectos básicos.
7.1 ¿En qué se diferencian la probabilidad y la estadística?
Antes de empezar a hablar de la teoría de la probabilidad, conviene dedicar un momento a reflexionar sobre la relación entre probabilidad y estadística. Ambas disciplinas están estrechamente relacionadas pero no son idénticas. La teoría de la probabilidad es “la doctrina de las probabilidades”. Es una rama de las matemáticas que nos dice con qué frecuencia ocurrirán diferentes tipos de sucesos. Por ejemplo, todas estas preguntas pueden responderse usando la teoría de la probabilidad:
- ¿Qué probabilidad hay de que una moneda salga cara 10 veces seguidas?
- Si tiro un dado de seis caras dos veces, ¿qué probabilidad hay de que saque dos seises?
- ¿Qué probabilidad hay de que cinco cartas extraídas de una baraja perfectamente barajada sean todas corazones?
- ¿Qué probabilidad hay de que gane la lotería?
Fíjate que todas estas preguntas tienen algo en común. En cada caso, se conoce la “verdad del mundo” y mi pregunta se refiere a “qué tipo de sucesos” ocurrirán. En la primera pregunta, sé que la moneda es justa, por lo que hay un 50% de probabilidades de que salga cara. En la segunda pregunta, sé que la probabilidad de sacar un 6 en un solo dado es de 1 entre 6. En la tercera pregunta, sé que la baraja se barajó correctamente. Y en la cuarta pregunta sé que la lotería sigue unas reglas específicas. Entiendes la idea. El punto crítico es que las preguntas probabilísticas empiezan con un modelo conocido del mundo, y usamos ese modelo para hacer algunos cálculos. El modelo subyacente puede ser bastante simple. Por ejemplo, en el ejemplo del lanzamiento de una moneda, podemos escribir el modelo así:
\[P(cara)=0.5\]
que se puede leer como “la probabilidad de que salga cara es 0,5”. Como veremos más adelante, del mismo modo que los porcentajes son números que van del 0% al 100%, las probabilidades son números que van del 0 al 1. Cuando utilizo este modelo de probabilidad para responder a la primera pregunta, en realidad no sé exactamente lo que va a pasar. Puede que salga, como dice la pregunta. Pero tal vez obtenga tres caras. Esa es la clave. En la teoría de la probabilidad se conoce el modelo, pero no los datos.
Eso es probabilidad. ¿Y la estadística? Las preguntas estadísticas funcionan al revés. En estadística no sabemos la verdad sobre el mundo. Lo único que tenemos son los datos y es a partir de ellos que queremos saber la verdad sobre el mundo. Las preguntas estadísticas tienden a parecerse más a estas:
- Si mi amigo lanza una moneda 10 veces y sale 10 caras, ¿me está gastando una broma?
- Si cinco cartas de la parte superior de la baraja son corazones, ¿qué probabilidad hay de que la baraja se haya barajado?
- Si el cónyuge del comisario de lotería gana la lotería, ¿qué probabilidad hay de que la lotería estuviera amañada?
Esta vez lo único que tenemos son datos. Lo que sé es que vi a mi amigo lanzar la moneda 10 veces y que salió cara todas las veces. Y lo que quiero deducir es si debo o no concluir que lo que acabo de ver era realmente una moneda justa lanzada 10 veces seguidas, o si debo sospechar que mi amigo me está gastando una broma. Los datos que tengo son los siguientes:
HHHHHHHHHHHH
y lo que intento es averiguar en qué “modelo del mundo” debo confiar. Si la moneda es justa, entonces el modelo que debo adoptar es el que dice que la probabilidad de que salga cara es 0.5, es decir P(cara) = 0,5. Si la moneda no es justa, debo concluir que la probabilidad de cara no es 0,5, lo que escribiríamos como \(P(cara)\ne{0,5}\). En otras palabras, el problema de la inferencia estadística consiste en averiguar cuál de estos modelos de probabilidad es correcto. Evidentemente, la pregunta estadística no es la misma que la pregunta de probabilidad, pero están profundamente conectadas entre sí. Debido a esto, una buena introducción a la teoría estadística comenzará con una discusión de lo que es la probabilidad y cómo funciona.
7.2 ¿Qué significa probabilidad?
Empecemos con la primera de estas preguntas. ¿Qué es “probabilidad”? Puede parecerte sorprendente, pero aunque los estadísticos y los matemáticos (en su mayoría) están de acuerdo en cuáles son las reglas de la probabilidad, hay mucho menos consenso sobre el significado real de la palabra. Parece extraño porque todos nos sentimos muy cómodos usando palabras como “azar”, “posible” y “probable”, y no parece que sea una pregunta muy difícil de responder. Pero si alguna vez has tenido esa experiencia en la vida real, es posible que se salgas de la conversación con la sensación de que no lo has entendido del todo y que (como muchos conceptos cotidianos) resulta que no sabes realmente de qué se trata.
Así que voy a intentarlo. Supongamos que quiero apostar en un partido de fútbol entre dos equipos de robots, el Arduino Arsenal y el C Milan. Después de pensarlo, decido que hay un 80% de probabilidad de que el Arduino Arsenal gane. ¿Qué quiero decir con eso? Aquí hay tres posibilidades:
- Son equipos de robots, así que puedo hacer que jueguen una y otra vez, y si lo hiciera, el Arduino Arsenal ganaría 8 de cada 10 juegos en promedio.
- Para cualquier partido, estaría de acuerdo en que apostar en este partido solo es “justo” si una apuesta de $1 al C Milan da un beneficio de $5 (es decir, recupero mi $1 más una recompensa de $4 por acertar), al igual que una apuesta de $4 al Arduino Arsenal (es decir, mi apuesta de $4 más una recompensa de $1).
- Mi “creencia” o “confianza” subjetiva en una victoria del Arduino Arsenal es cuatro veces mayor que mi creencia en una victoria del C Milan.
Cada una de ellas parece sensata. Sin embargo, no son idénticas y no todos los estadísticos las respaldarían todas. La razón es que existen diferentes ideologías estadísticas (sí, de verdad) y dependiendo de a cuál te suscribas, podrías decir que algunas de esas afirmaciones no tienen sentido o son irrelevantes. En esta sección presento brevemente los dos enfoques principales que existen en la literatura. No son ni mucho menos los únicos enfoques, pero son los dos grandes.
7.2.1 La vista frecuentista
El primero de los dos enfoques principales de la probabilidad, y el más dominante en estadística, se conoce como la visión frecuentista y define la probabilidad como una frecuencia a largo plazo. Supongamos que intentamos lanzar una moneda al aire una y otra vez. Por definición, se trata de una moneda que tiene \(P(C) = 0,5\). ¿Qué podríamos observar? Una posibilidad es que los primeros 20 lanzamientos tengan este aspecto:
T,H,H,H,H,T,T,H,H,H,H,T,H,H,T,T,T,T,T,H
En este caso, 11 de estos 20 lanzamientos (55%) han salido cara. Supongamos ahora que llevo la cuenta del número de caras (que llamaré \(N_H\)) que he visto, en los primeros N lanzamientos, y calculo la proporción de caras \(\frac{N_H} {N}\) cada vez. La Table 7.1 muestra lo que obtendría (literalmente lancé monedas para producir esto):
Observa que al principio de la secuencia, la proporción de caras fluctúa enormemente, empezando por \(.00\) y subiendo hasta \(.80\). Más tarde, se tiene la impresión de que se atenúa un poco, y cada vez más los valores se acercan a la respuesta “correcta” de \(.50\). Esta es la definición frecuentista de probabilidad en pocas palabras. Lanzar una moneda una y otra vez, y a medida que N crece (se acerca al infinito, denotado \(N \rightarrow \infty\) ) la proporción de caras convergerá al 50%. Hay algunos tecnicismos sutiles que preocupan a los matemáticos, pero cualitativamente hablando, así es como los frecuentistas definen la probabilidad. Desafortunadamente, no tengo un número infinito de monedas o la paciencia infinita necesaria para lanzar una moneda un número infinito de veces. Sin embargo, tengo un ordenador y los ordenadores destacan en tareas repetitivas sin sentido. Así que le pedí a mi ordenador que simulara lanzar una moneda 1000 veces y luego hice un dibujo de lo que ocurre con la proporción \(\frac{N_H}{N}\) a medida que aumenta \(N\). De hecho, lo hice cuatro veces para asegurarme de que no fuera una casualidad. Los resultados se muestran en Figure 7.1. Como puedes ver, la proporción de caras observadas deja de fluctuar y se estabiliza. Cuando lo hace, el número en el que finalmente se asienta es la verdadera probabilidad de caras.
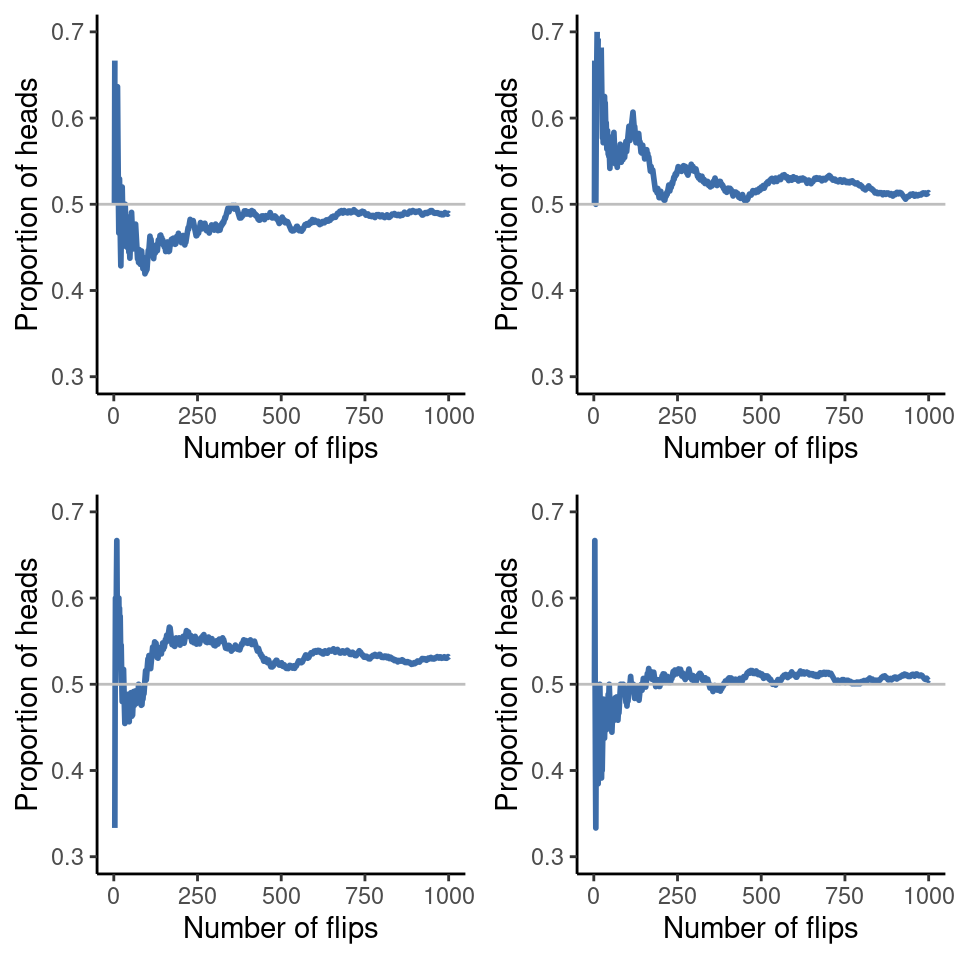
La definición frecuentista de probabilidad tiene algunas características deseables. En primer lugar, es objetiva. La probabilidad de un suceso está necesariamente fundamentada en el mundo. Las afirmaciones sobre la probabilidad sólo tienen sentido si se refieren a (una secuencia de) sucesos que ocurren en el universo físico.1 En segundo lugar, no es ambigua. Si dos personas observan la misma secuencia de acontecimientos e intentan calcular la probabilidad de un suceso, inevitablemente obtendrán la misma respuesta.
Sin embargo, también tiene características indeseables. En primer lugar, las secuencias infinitas no existen en el mundo físico. Supongamos que cogemos una moneda del bolsillo y empezamos a lanzarla. Cada vez que cae, impacta contra el suelo. Cada impacto desgasta un poco la moneda. Al final, la moneda se destruye. Por tanto, cabe preguntarse si realmente tiene sentido pretender que una secuencia “infinita” de lanzamientos de monedas es siquiera un concepto significativo u objetivo. No podemos decir que una “secuencia infinita” de sucesos sea algo real en el universo físico, porque el universo físico no permite nada infinito. Y lo que es más grave, la definición frecuentista tiene un alcance limitado. Hay muchas cosas a las que los seres humanos asignan probabilidades en el lenguaje cotidiano, pero que no pueden (ni siquiera en teoría) asignarse a una secuencia hipotética de sucesos. Por ejemplo, si un meteorólogo sale en la televisión y dice “la probabilidad de que llueva en Adelaide el 2 de noviembre de 2048 es del 60%”, los seres humanos lo aceptamos de buen grado. Pero no está claro cómo definir esto en términos frecuentistas. Solo hay una ciudad, Adelaide, y solo un 2 de noviembre de 2048. Aquí no hay una secuencia infinita de eventos, solo algo único. La probabilidad frecuentista nos prohibe hacer afirmaciones probabilísticas sobre un único suceso. Desde la perspectiva frecuentista, mañana lloverá o no lloverá. No existe una “probabilidad” asociada a un único suceso no repetible. Ahora bien, hay que decir que los frecuentistas pueden utilizar algunos trucos muy ingeniosos para evitar esto. Una posibilidad es que lo que quiere decir el meteorólogo sea algo así como “Hay una categoría de días para los que predigo un 60% de probabilidad de lluvia, y si nos fijamos solo en los días para los que hago esta predicción, entonces el 60% de esos días lloverá de verdad”. Es muy extraño y contraintuitivo pensar de este modo, pero los frecuentistas a veces lo hacen. Y aparecerá más adelante en este libro (por ejemplo, en Section 8.5).
7.2.2 La vista bayesiana
El punto de vista bayesiano de la probabilidad suele denominarse subjetivista y, aunque ha sido un punto de vista minoritario entre los estadísticos, ha ido ganando terreno en las últimas décadas. Hay muchos tipos de bayesianismo, por lo que es difícil decir exactamente cuál es “la” visión bayesiana. La forma más común de pensar en la probabilidad subjetiva es definir la probabilidad de un acontecimiento como el grado de creencia que un agente inteligente y racional asigna a la verdad de ese suceso. Desde esa perspectiva, las probabilidades no existen en el mundo sino en los pensamientos y suposiciones de las personas y otros seres inteligentes.
Sin embargo, para que este enfoque funcione necesitamos alguna forma de operacionalizar el “grado de creencia”. Una forma de hacerlo es formalizarlo en términos de “juego racional”, aunque hay muchas otras formas. Supongamos que creo que hay un 60% de probabilidades de que llueva mañana. Si alguien me ofrece una apuesta en la que si llueve mañana gano $5, pero si no llueve pierdo $5 está claro que, desde mi perspectiva, es una apuesta bastante buena. En cambio, si creo que la probabilidad de que llueva es solo del 40%, entonces es una mala apuesta. Así que podemos operacionalizar la noción de “probabilidad subjetiva” en términos de qué apuestas estoy dispuesta a aceptar.
¿Cuáles son las ventajas y desventajas del enfoque bayesiano? La principal ventaja es que permite asignar probabilidades a cualquier suceso que se desee. No es necesario limitarse a los sucesos repetibles. La principal desventaja (para mucha gente) es que no podemos ser puramente objetivos. Especificar una probabilidad requiere que especifiquemos una entidad que tenga el grado de creencia relevante. Esta entidad puede ser un ser humano, un extraterrestre, un robot o incluso un estadístico. Pero tiene que haber un agente inteligente que crea en las cosas. Para mucha gente esto es incómodo, parece que hace que la probabilidad sea arbitraria. Aunque el enfoque bayesiano exige que el agente en cuestión sea racional (es decir, que obedezca a las reglas de la probabilidad), permite que cada uno tenga sus propias creencias. Yo puedo creer que la moneda es justa y tú no, aunque ambos seamos racionales. La visión frecuentista no permite que dos observadores atribuyan diferentes probabilidades a un mismo suceso. Cuando eso ocurre, al menos uno de ellos debe estar equivocado. La visión bayesiana no impide que esto ocurra. Dos observadores con diferentes conocimientos previos pueden legítimamente tener diferentes creencias sobre el mismo suceso. En resumen, mientras que la visión frecuentista a veces se considera demasiado estrecha (prohibe muchas cosas a las que queremos asignar probabilidades), la visión bayesiana a veces se considera demasiado amplia (permite demasiadas diferencias entre los observadores).
7.2.3 ¿Cual es la diferencia? ¿Y quién tiene razón?
Ahora que has visto cada uno de estos dos puntos de vista de forma independiente, es útil que te asegures que puedes compararlos. Vuelve al hipotético partido de fútbol de robots del principio de la sección. ¿Qué crees que dirían un frecuentista y un bayesiano sobre estas tres afirmaciones? ¿Qué afirmación diría un frecuentista que es la definición correcta de probabilidad? ¿Por cuál optaría un bayesiano? ¿Algunas de estas afirmaciones carecerían de sentido para un frecuentista o un bayesiano? Si has entendido las dos perspectivas, deberías tener alguna idea de cómo responder a estas preguntas.
Bien, suponiendo que entiendas la diferencia, te estarás preguntando cuál de ellos tiene razón. Sinceramente, no sé si hay una respuesta correcta. Hasta donde yo sé, no hay nada matemáticamente incorrecto en la forma en que los frecuentistas piensan sobre las secuencias de acontecimientos, y no hay nada matemáticamente incorrecto en la forma en que los bayesianos definen las creencias de un agente racional. De hecho, cuando profundizas en los detalles, bayesianos y frecuentistas coinciden en muchas cosas. Muchos métodos frecuentistas conducen a decisiones que los bayesianos están de acuerdo en que tomaría un agente racional. Muchos métodos bayesianos tienen muy buenas propiedades frecuentistas.
En general, soy pragmática, así que usaré cualquier método estadístico en el que confíe. Resulta que prefiero los métodos bayesianos por razones que explicaré al final del libro. Pero no me opongo fundamentalmente a los métodos frecuentistas. No todo el mundo está tan relajado. Por ejemplo, consideremos a Sir Ronald Fisher, una de las figuras más destacadas de la estadística del siglo XX y un opositor vehemente a todo lo bayesiano, cuyo artículo sobre los fundamentos matemáticos de la estadística se refería a la probabilidad bayesiana como “una jungla impenetrable [que] detiene el progreso hacia la precisión de los conceptos estadísticos” (Fisher, 1922, p. 311). O el psicólogo Paul Meehl, quien sugiere que confiar en los métodos frecuentistas podría convertirte en “un libertino intelectual potente pero estéril que deja en su alegre camino una larga cola de doncellas violadas pero ninguna descendencia científica viable” (Meehl, 1967, p. 114). La historia de la estadística, como se puede deducir, no está exenta de entretenimiento.
En cualquier caso, aunque personalmente prefiero la visión bayesiana, la mayoría de los análisis estadísticos se basan en el enfoque frecuentista. Mi razonamiento es pragmático. El objetivo de este libro es cubrir aproximadamente el mismo territorio que una clase típica de estadística de grado en psicología, y si quieres entender las herramientas estadísticas utilizadas por la mayoría de los psicólogos y psicólogas, necesitarás una buena comprensión de los métodos frecuentistas. Te prometo que no es un esfuerzo en vano. Incluso si al final quieres pasarte a la perspectiva bayesiana, deberías leer al menos un libro sobre la visión frecuentista “ortodoxa”. Además, no no voy a ignorar por completo la perspectiva bayesiana. De vez en cuando añadiré algún comentario desde un punto de vista bayesiano, y volveré a tratar el tema con más profundidad en Chapter 16.
7.3 Teoría básica de la probabilidad
A pesar de las discusiones ideológicas entre bayesianos y frecuentistas, resulta que la mayoría de la gente está de acuerdo en las reglas que deben seguir las probabilidades. Hay muchas maneras diferentes de llegar a estas reglas. El método más utilizado se basa en el trabajo de Andrey Kolmogorov, uno de los grandes matemáticos soviéticos del siglo XX. No entraré en muchos detalles, pero intentaré darte una idea de cómo funciona. Y para ello voy a tener que hablar de mis pantalones.
7.3.1 Introducción a las distribuciones de probabilidad
Una de las verdades más inquietantes de mi vida es que solo tengo 5 pares de pantalones. Tres vaqueros, la mitad inferior de un traje y un pantalón de chándal. Y lo que es más triste, les he puesto nombres: los llamo \(X_1\), \(X_2\), \(X_3\), \(X_4\) y \(X_5\). De verdad, por eso me llaman Mister Imaginative. Ahora, en un día cualquiera, elijo exactamente un pantalón para ponerme. Ni siquiera yo soy tan estúpido como para intentar llevar dos pares de pantalones, y gracias a años de entrenamiento ya nunca salgo a la calle sin usar pantalones. Si tuviera que describir esta situación usando el lenguaje de la teoría de la probabilidad, me referiría a cada par de pantalones (es decir, cada \(X\)) como un suceso elemental. La característica clave de los sucesos elementales es que cada vez que hacemos una observación (p. ej., cada vez que me pongo unos pantalones), el resultado será uno y solo uno de estos sucesos. Como he dicho, estos días siempre llevo exactamente un pantalón, así que mis pantalones satisfacen esta restricción. Del mismo modo, el conjunto de todos los sucesos posibles se denomina espacio muestral. Es cierto que algunas personas lo llamarían “armario”, pero eso es porque se niegan a pensar en mis pantalones en términos probabilísticos. Qué triste.
Bien, ahora que tenemos un espacio muestral (un armario), que se construye a partir de muchos sucesos elementales posibles (pantalones), lo que queremos hacer es asignar una probabilidad a uno de estos sucesos elementales. Para un suceso \(X\), la probabilidad de ese suceso \(P(X)\) es un número comprendido entre 0 y 1. Cuanto mayor sea el valor de \(P(X)\), más probable es que ocurra el suceso. Así, por ejemplo, si \(P(X) = 0\) significa que el suceso \(X\) es imposible (es decir, nunca me pongo esos pantalones). Por otro lado, si \(P(X) = 1\) significa que el suceso \(X\) seguramente ocurrirá (es decir, siempre llevo esos pantalones). Para valores de probabilidad intermedios significa que a veces llevo esos pantalones. Por ejemplo, si \(P(X) = 0.5\) significa que llevo esos pantalones la mitad de las veces.
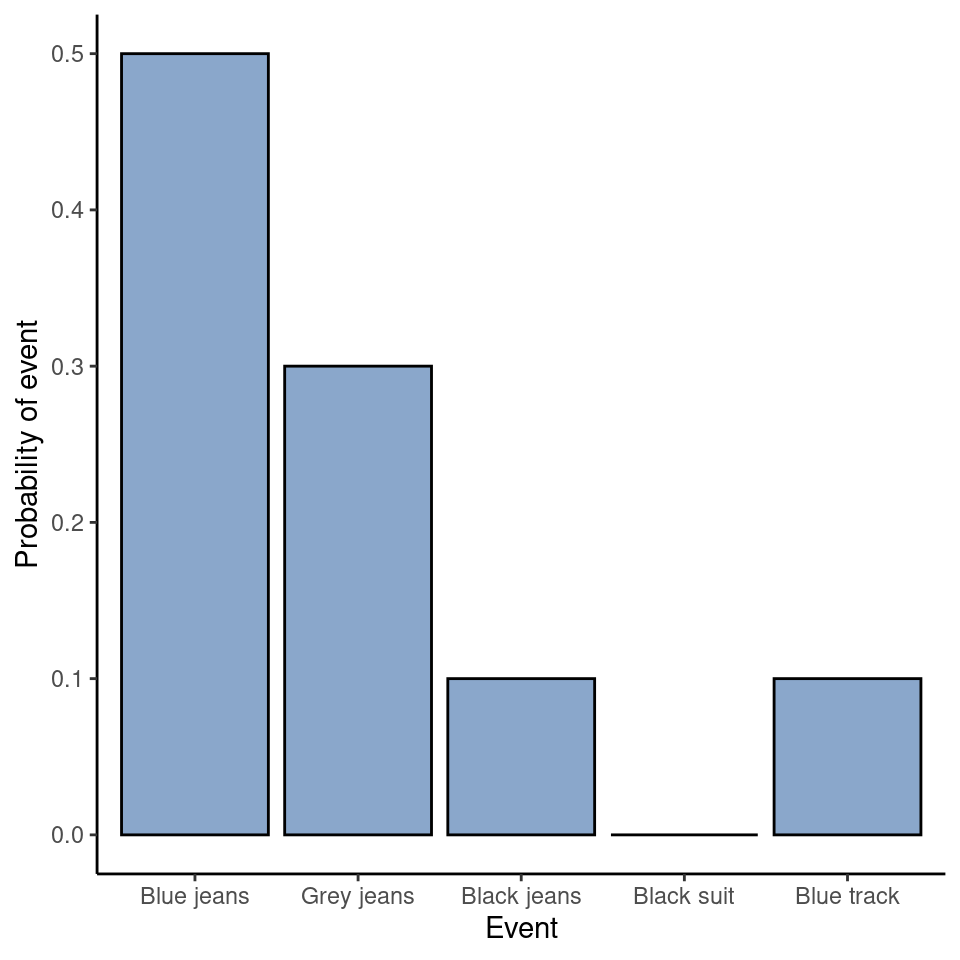
Llegados a este punto, casi hemos terminado. Lo último que debemos reconocer es que “siempre pasa algo”. Cada vez que me pongo unos pantalones, realmente acabo llevando pantalones (loco, ¿no?). Lo que significa esta afirmación un tanto trillada, en términos probabilísticos, es que las probabilidades de los sucesos elementales tienen que sumar 1. Esto se conoce como la ley de probabilidad total, aunque a ninguna de nosotras nos importe realmente. Y lo que es más importante, si se cumplen estos requisitos, lo que tenemos es una distribución de probabilidad. Por ejemplo, la Table 7.2 muestra un ejemplo de una distribución de probabilidad.
| Which trousers? | Label | Probability |
|---|---|---|
| Blue jeans | \(X_1 \) | \(P(X_1)=.5 \) |
| Grey jeans | \(X_2 \) | \(P(X_2)=.3 \) |
| Black jeans | \(X_3 \) | \(P(X_3)=.1 \) |
| Black suit | \(X_4 \) | \(P(X_4)=0 \) |
| Blue tracksuit | \(X_5 \) | \(P(X_5)=.1 \) |
Cada uno de los sucesos tiene una probabilidad comprendida entre 0 y 1, y si sumamos las probabilidades de todos los sucesos, suman 1. Impresionante. Incluso podemos dibujar un bonito gráfico de barras (ver Section 5.3) para visualizar esta distribución, como se muestra en la Figure 7.2. Y, llegados a este punto, todos hemos conseguido algo. Aprendiste lo que es una distribución de probabilidad y yo, por fin, encontré una manera de crear un gráfico que se centre por completo en mis pantalones. ¡Todo el mundo gana! Lo único que tengo que decir es que la teoría de la probabilidad permite hablar tanto de sucesos no elementales como de los elementales. La forma más fácil de ilustrar el concepto es con un ejemplo. En el ejemplo de los pantalones, es perfectamente legítimo referirse a la probabilidad de que yo lleve vaqueros. En este escenario, el suceso “Dani lleva vaqueros” se dice que ha ocurrido siempre que el suceso elemental que realmente ocurrió sea uno de los apropiados. En este caso “vaqueros azules”, “vaqueros negros” o “vaqueros grises”. En términos matemáticos definimos el suceso “vaqueros” \(E\) como el conjunto de sucesos elementales \((X1, X2, X3)\). Si se produce alguno de estos sucesos elementales, también se dice que se ha producido \(E\). Habiendo decidido escribir la definición del E de esta manera, es bastante sencillo establecer cuál es la probabilidad P(E) y, puesto que las probabilidades de los vaqueros azules, grises y negros respectivamente son \(.5\), \(.3\) y $ .1$, la probabilidad de que lleve vaqueros es igual a \(.9\). es: simplemente lo sumamos todo. En este caso concreto, \[P(E)=P(X_1)+P(X_2)+P(X_3)\] Llegados a este punto, puede que estés pensando que todo esto es terriblemente obvio y sencillo y estarías en lo cierto. En realidad, lo único que hemos hecho es envolver unas cuantas intuiciones de sentido común con algunas matemáticas básicas. Sin embargo, a partir de estos sencillos principios es posible construir algunas herramientas matemáticas extremadamente potentes. No voy a entrar en detalles en este libro, pero lo que sí voy a hacer es enumerar, en la Table 7.3, algunas de las otras reglas que satisfacen las probabilidades. Estas reglas se pueden derivar de los supuestos básicos que he descrito anteriormente, pero como en realidad no usamos estas reglas para nada en este libro, no lo haré aquí.
| English | Notation | Formula |
|---|---|---|
| not A | \(P (\neg A) \) | \(1-P(A) \) |
| A or B | \(P(A \cup B) \) | \(P(A) + P(B) - P(A \cap B) \) |
| A and B | \(P(A \cap B) \) | \(P(A|B) P(B) \) |
7.4 La distribución binomial
Como puedes imaginar, las distribuciones de probabilidad varían enormemente y existe una gran variedad de distribuciones. Sin embargo, no todas tienen la misma importancia. De hecho, la mayor parte del contenido de este libro se basa en una de cinco distribuciones: la distribución binomial, la distribución normal, la distribución t, la distribución \(\chi^2\) (“ji-cuadrado”) y la distribución F . Por ello, lo que haré en las próximas secciones será una breve introducción a estas cinco distribuciones, prestando especial atención a la binomial y la normal. Empezaré por la distribución binomial ya que es la más sencilla de las cinco.
7.4.1 Introducción a la distribución binomial
La teoría de la probabilidad se originó en el intento de describir cómo funcionan los juegos de azar, por lo que parece apropiado que nuestra discusión sobre la distribución binomial incluya una discusión sobre tirar dados y lanzar monedas. Imaginemos un sencillo “experimento”. En mi mano tengo 20 dados idénticos de seis caras. En una cara de cada dado hay una imagen de una calavera, las otras cinco caras están en blanco. Si tiro los 20 dados, ¿cuál es la probabilidad de que obtenga exactamente 4 calaveras? Suponiendo que los dados sean justos, sabemos que la probabilidad de que salga una calavera es de 1 entre 6. Dicho de otro modo, la probabilidad de que salga una calavera con un solo dado es de aproximadamente 0,167. Esta información es suficiente para responder a nuestra pregunta, así que veamos cómo se hace.
Como de costumbre, tendremos que introducir algunos nombres y alguna notación. Dejaremos que \(N\) denote el número de lanzamientos de dados en nuestro experimento, cantidad que suele denominarse parámetro de tamaño de nuestra distribución binomial. También usaremos \(\theta\) para referirnos a la probabilidad de que un solo dado salga calavera, cantidad que generalmente se denomina probabilidad de éxito de la binomial.2 Finalmente, usaremos \(X\) para referirnos a los resultados de nuestro experimento, es decir, el número de calaveras que obtengo al tirar los dados. Dado que el valor real de \(X\) se debe al azar, nos referimos a él como variable aleatoria. En cualquier caso, ahora que tenemos toda esta terminología y notación podemos usarla para plantear el problema con un poco más de precisión. La cantidad que queremos calcular es la probabilidad de que \(X = 4\) dado que sabemos que \(\theta = .167\) y \(N = 20\). La “forma” general de lo que me interesa calcular podría escribirse como
\[P(X|\theta,N)\]
y nos interesa el caso especial donde \(X = 4, \theta = .167\) y \(N = 20\).
[Detalle técnico adicional 3]
Sí, sí. Sé lo que estás pensando: notación, notación, notación. Realmente, ¿a quién le importa? Muy pocos lectores de este libro están aquí por la notación, así que probablemente debería continuar y hablar de cómo utilizar la distribución binomial. He incluido la fórmula de la distribución binomial en una nota a pie de página 4, ya que algunos lectores pueden querer jugar con ella por sí mismos, pero como a la mayoría de la gente probablemente no le importe mucho y porque no necesitamos la fórmula en este libro, no hablaré de ella en detalle. En su lugar, solo quiero mostrarte cómo es la distribución binomial.
Para ello, la Figure 7.3 muestra las probabilidades binomiales para todos los valores posibles de \(X\) para nuestro experimento de lanzamiento de dados, desde \(X = 0\) (sin calaveras) hasta \(X = 20\) (todas las calaveras). Ten en cuenta que esto es básicamente un gráfico de barras, y no difiere en nada del gráfico de “probabilidad de los pantalones” que dibujé en la Figure 7.2. En el eje horizontal tenemos todos los sucesos posibles y en el eje vertical podemos leer la probabilidad de cada uno de esos sucesos. Así, la probabilidad de sacar calaveras de \(4\) de \(20\) es de aproximadamente \(0,20\) (la respuesta real es \(0,2022036\), como veremos en un momento). En otras palabras, esperarías que ocurriera alrededor del 20% de las veces que repitieras este experimento.

Para que nos hagamos una idea de cómo cambia la distribución binomial cuando modificamos los valores de \(theta\) y \(N\), supongamos que, en lugar de tirar los dados, lo que hago es lanzar monedas. Esta vez, mi experimento consiste en lanzar una moneda al aire repetidamente y el resultado que me interesa es el número de caras que observo. En este escenario, la probabilidad de éxito ahora es \(\theta = \frac{1}{2}\). Supongamos que lanzo la moneda \(N = 20\) veces. En este ejemplo, he cambiado la probabilidad de éxito pero he mantenido el mismo tamaño del experimento. ¿Cómo afecta esto a nuestra distribución binomial? Bueno, como muestra la Figure 7.4, el efecto principal de esto es desplazar toda la distribución, como era de esperar. Bien, ¿y si lanzamos una moneda \(N = 100\) veces? Bueno, en ese caso obtenemos la Figure 7.4 (b). La distribución se mantiene aproximadamente en el centro, pero hay un poco más de variabilidad en los posibles resultados.

7.5 La distribución normal
Aunque la distribución binomial es conceptualmente la más sencilla de entender, no es la más importante. Ese honor particular corresponde a la distribución normal, también conocida como “la curva de campana” o “distribución gaussiana”. Una distribución normal se describe utilizando dos parámetros: la media de la distribución µ y la desviación estándar de la distribución \(\sigma\).
[Detalle técnico adicional 5]
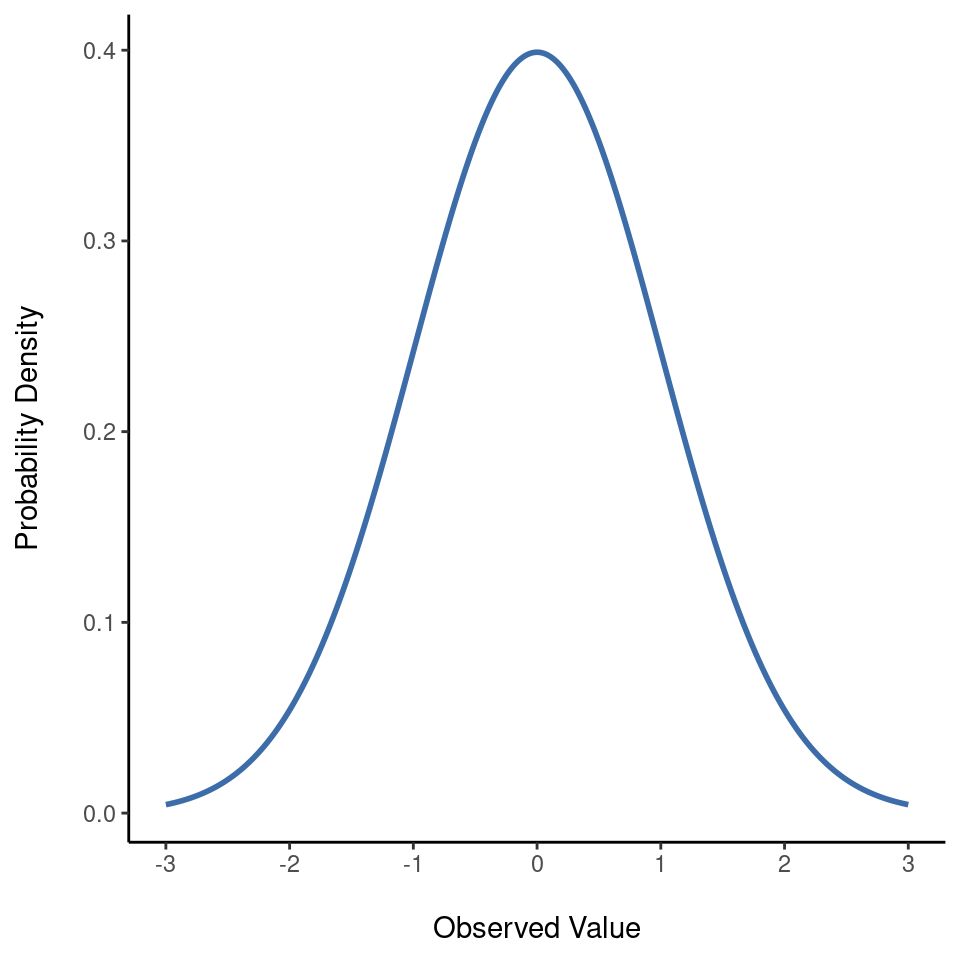
Intentemos hacernos una idea de lo que significa que una variable se distribuya normalmente. Para ello, observa la Figure 7.5 que representa una distribución normal con media \(\mu = 0\) y desviación estándar \(\sigma = 1\). Puedes ver de dónde viene el nombre “curva de campana”; se parece un poco a una campana. Observa que, a diferencia de los gráficos que he dibujado para ilustrar la distribución binomial, la imagen de la distribución normal de la Figure 7.5 muestra una curva suave en lugar de barras “tipo histograma”. No se trata de una elección arbitraria, ya que la distribución normal es continua, mientras que la binomial es discreta. Por ejemplo, en el ejemplo del dado de la sección anterior era posible obtener 3 calaveras o 4 calaveras, pero era imposible obtener 3,9 calaveras. Las figuras que dibujé en el apartado anterior reflejan este hecho. En la Figure 7.3, por ejemplo, hay una barra situada en \(X = 3\) y otra en \(X = 4\) pero no hay nada en medio. Las cantidades continuas no tienen esta restricción. Por ejemplo, supongamos que hablamos del tiempo. La temperatura en un agradable día de primavera podría ser de 23 grados, 24 grados, 23,9 grados o cualquier valor intermedio, ya que la temperatura es una variable continua. Por tanto, una distribución normal podría ser muy adecuada para describir las temperaturas primaverales6
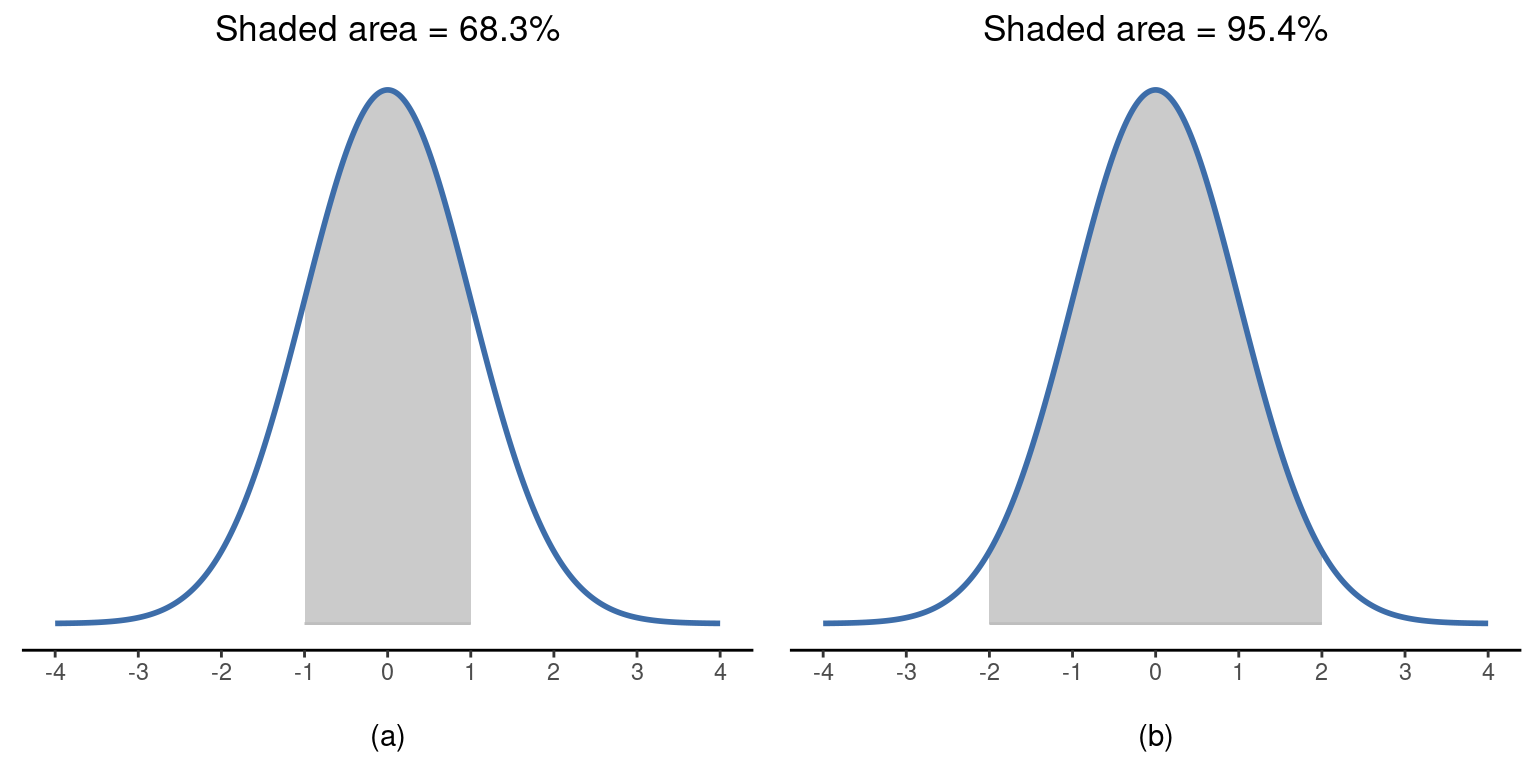
Teniendo esto en cuenta, veamos si podemos intuir cómo funciona la distribución normal. En primer lugar, veamos qué ocurre cuando jugamos con los parámetros de la distribución. Para ello, en la Figure 7.6 se representan distribuciones normales con medias diferentes pero con la misma desviación estándar. Como era de esperar, todas estas distribuciones tienen la misma “anchura”. La única diferencia entre ellas es que se han desplazado a la izquierda o a la derecha. Por lo demás, son idénticas. Por el contrario, si aumentamos la desviación estándar manteniendo la media constante, el pico de la distribución se mantiene en el mismo lugar, pero la distribución se ensancha, como se puede ver en la Figure 7.7. Sin embargo, observa que cuando ampliamos la distribución, la altura del pico disminuye. Esto tiene que suceder, del mismo modo que las alturas de las barras que usamos para dibujar una distribución binomial discreta deben sumar 1, el área total bajo la curva de la distribución normal debe ser igual a 1. Antes de continuar, quiero señalar una característica importante de la distribución normal. Independientemente de cuál sea la media real y la desviación estándar, \(68,3\%\) del área cae dentro de 1 desviación estándar de la media. Del mismo modo, \(95,4\%\) de la distribución cae dentro de 2 desviaciones estándar de la media, y \((99,7\%)\) de la distribución está dentro de 3 desviaciones estándar. Esta idea se ilustra en la Figure 7.8; ver también la Figure 7.9.


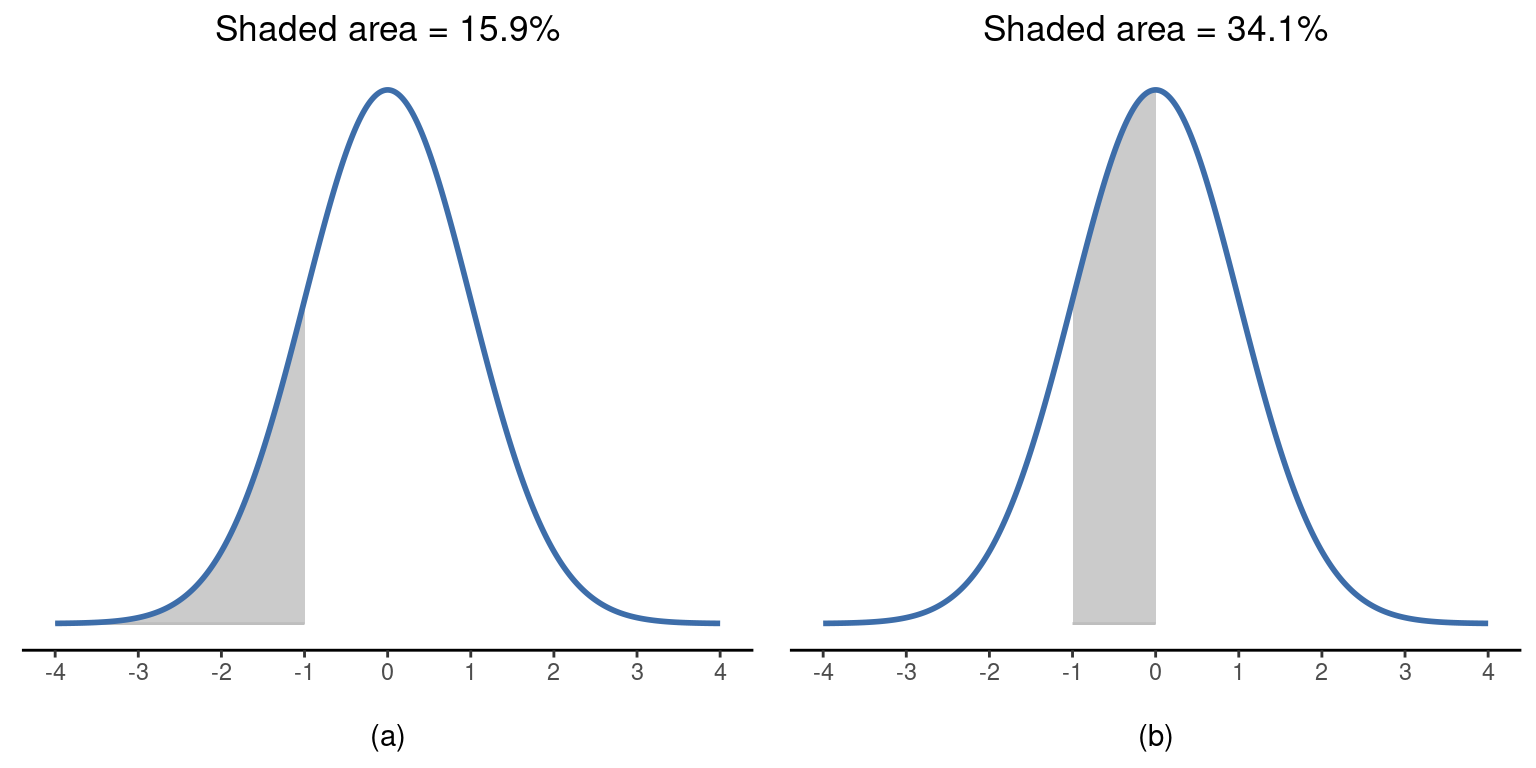
7.5.1 Densidad de probabilidad
Hay algo que he intentado ocultar a lo largo de mi discusión sobre la distribución normal, algo que algunos libros de texto introductorios omiten por completo. Puede que tengan razón al hacerlo. Esta “cosa” que estoy ocultando es extraña y contraintuitiva, incluso para los estándares distorsionados que se aplican en estadística. Afortunadamente, no es algo que haya que entender a un nivel profundo para hacer estadística básica. Más bien, es algo que empieza a ser importante más adelante, cuando se va más allá de lo básico. Así que, si no tiene mucho sentido, no te preocupes demasiado, pero intenta asegurarte de que entiendes lo esencial.
A lo largo de mi exposición sobre la distribución normal ha habido una o dos cosas que no acaban de tener sentido. Quizás te hayas dado cuenta de que el eje y de estas figuras está etiquetado como “Densidad de probabilidad” en lugar de densidad. Tal vez te hayas dado cuenta de que he utilizado \(P(X)\) en lugar de \(P(X)\) al dar la fórmula de la distribución normal.
Resulta que lo que se presenta aquí no es en realidad una probabilidad, es otra cosa. Para entender qué es ese algo, hay que dedicar un poco de tiempo a pensar qué significa realmente decir que \(X\) es una variable continua. Digamos que estamos hablando de la temperatura exterior. El termómetro me dice que hace \(23\) grados, pero sé que eso no es realmente cierto. No son exactamente \(23\) grados. Tal vez sean \(23.1\) grados, pienso. Pero sé que eso tampoco es realmente cierto porque puede que sean $ 23.09 $ grados. Pero sé que… bueno, entiendes la idea. Lo complicado de las cantidades realmente continuas es que nunca se sabe exactamente lo que son.
Ahora piensa en lo que esto implica cuando hablamos de probabilidades. Supongamos que la temperatura máxima de mañana se muestra a partir de una distribución normal con una media \(23\) y desviación estándar 1. ¿Cuál es la probabilidad de que la temperatura sea exactamente de \(23\) grados? La respuesta es “cero”, o posiblemente “un número tan cercano a cero que bien podría ser cero”. ¿A qué se debe esto? Es como intentar lanzar un dardo a una diana infinitamente pequeña. Por muy buena puntería que tengas, nunca acertarás. En la vida real, nunca obtendrás un valor de exactamente $ 23 $. Siempre será algo como $ 23,1 $ o $ 22,99998 $ o algo así. En otras palabras, no tiene ningún sentido hablar de la probabilidad de que la temperatura sea exactamente de \(23\) grados. Sin embargo, en el lenguaje cotidiano, si te dijera que afuera había $23 grados y resultara que hace $22,9998, probablemente no me llamarías mentirosa. Porque en el lenguaje cotidiano “\(23\) grados” suele significar algo así como “algo entre \(22,5\) y \(23,5\) grados”. Y aunque no parece muy significativo preguntar sobre la probabilidad de que la temperatura sea exactamente de \(23\) grados, sí parece sensato preguntar sobre la probabilidad de que la temperatura esté entre \(22,5\) y \(23,5\), o entre \(20\) y \(30\). , o cualquier otro rango de temperaturas.
El objetivo de esta discusión es dejar claro que, cuando hablamos de distribuciones continuas, no tiene sentido hablar de la probabilidad de un valor concreto. Sin embargo, de lo que sí podemos hablar es de la probabilidad de que el valor se encuentre dentro de un rango concreto de valores. Para averiguar la probabilidad asociada a un rango particular, lo que hay que hacer es calcular el “área bajo la curva”. Ya hemos visto este concepto, en la Figure 7.8 las áreas sombreadas muestran probabilidades reales (p. ej., en la Figure 7.8 muestra la probabilidad de observar un valor que se encuentra dentro de 1 desviación estándar de la media).
Vale, eso explica parte de la historia. He explicado un poco acerca de cómo las distribuciones continuas de probabilidad deben ser interpretadas (es decir, el área bajo la curva es la clave). Pero, ¿qué significa realmente la fórmula para ppxq que he descrito antes? Obviamente, \(P(x)\) no describe una probabilidad, pero ¿qué es? El nombre de esta cantidad \(P(x)\) es densidad de probabilidad y, en términos de los gráficos que hemos estado dibujando, corresponde a la altura de la curva. Las densidades en sí mismas no son significativas, pero están “amañadas” para garantizar que el área bajo la curva siempre se pueda interpretar como probabilidades genuinas. Para ser sincera, eso es todo lo que necesitas saber por ahora.7
7.6 Otras distribuciones útiles
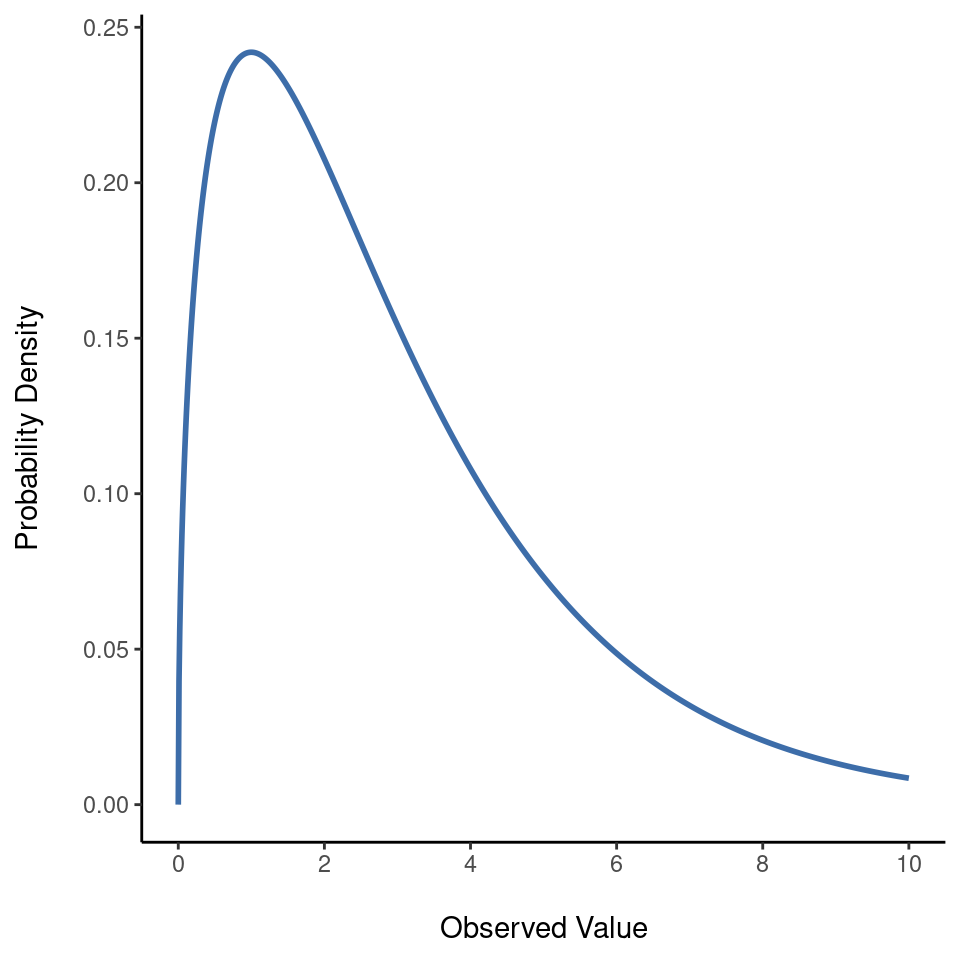
La distribución normal es la que más utiliza en estadística (por razones que veremos en breve), y la distribución binomial es muy útil para muchos propósitos. Pero el mundo de la estadística está lleno de distribuciones de probabilidad, algunas de las cuales veremos de pasada. En concreto, las tres que aparecerán en este libro son la distribución t, la distribución \(\chi^2\) y la distribución F. No daré fórmulas para ninguna de ellas, ni hablaré de ellas con demasiado detalle, pero mostraré algunas imágenes: Figure 7.10, Figure 7.11 y Figure 7.12.
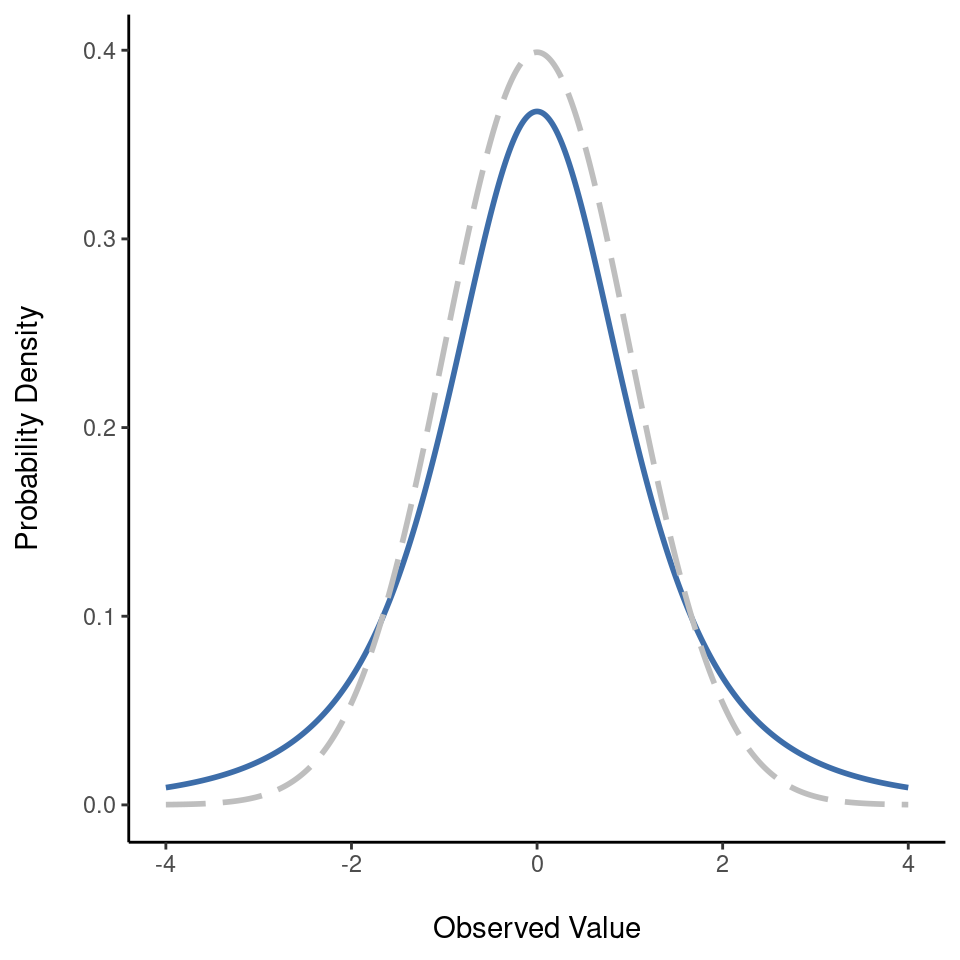

- La distribución \(t\) es una distribución continua que se parece mucho a una distribución normal, consulta la Figure 7.10. Observa que las “colas” de la distribución t son “más pesadas” (es decir, se extienden más hacia afuera) que las colas de la distribución normal. Esa es la diferencia importante entre ambas. Esta distribución suele aparecer en situaciones en las que se cree que los datos en realidad siguen una distribución normal, pero se desconoce la media o la desviación estándar. Nos encontraremos con esta distribución nuevamente en Chapter 11.
- La distribución \(\chi^2\) es otra distribución que aparece en muchos lugares diferentes. La situación en la que la veremos será cuando hagamos un análisis de datos categóricos en Chapter 10, pero es una de esas cosas que aparecen por todas partes. Cuando se profundiza en las matemáticas (¿y a quién no le gusta hacerlo?), resulta que la razón principal por la que la distribución \(\chi^2\) aparece por todas partes es que si tienes un montón de variables que se distribuyen normalmente, se elevan al cuadrado sus valores y luego se suman (un procedimiento conocido como “suma de cuadrados”), esta suma tiene una distribución \(\chi^2\). Te sorprendería saber con qué frecuencia este hecho resulta útil. De todos modos, así es como se ve una distribución \(\chi^2\): Figure 7.11.
- La distribución \(F\) se parece un poco a una distribución \(\chi^2\), y surge siempre que se necesita comparar dos distribuciones \(\chi^2\) entre sí. Hay que reconocer que esto no suena exactamente como algo que cualquier persona en su sano juicio querría hacer, pero resulta ser muy importante en el análisis de datos del mundo real. ¿Recuerdas cuando dije que \(\chi^2\) resulta ser la distribución clave cuando tomamos una “suma de cuadrados”? Bueno, lo que eso significa es que si quieres comparar dos “sumas de cuadrados” diferentes, probablemente estés hablando de algo que tiene una distribución F. Por supuesto, aún no te he dado un ejemplo de algo que involucre una suma de cuadrados, pero lo haré en Chapter 13. Y ahí es donde veremos la distribución F. Ah, y hay una imagen en la Figure 7.12.
Bien, es hora de terminar esta sección. Hemos visto tres distribuciones nuevas: \(\chi^2\)), \(t\) y \(F\). Todas son distribuciones continuas y están estrechamente relacionadas con la distribución normal. Lo principal para nuestros propósitos es que comprendas la idea básica de que estas distribuciones están profundamente relacionadas entre sí y con la distribución normal. Más adelante en este libro nos encontraremos con datos que se distribuyen normalmente, o que al menos se supone que se distribuyen normalmente. Lo que quiero que entiendas ahora es que, si asumes que tus datos se distribuyen normalmente, no deberías sorprenderte al ver las distribuciones \(\chi^2\), \(t\) y \(F\) apareciendo por todas partes cuando empieces a intentar hacer tu análisis de datos.
7.7 Resumen
En este capítulo hemos hablado de la probabilidad. Hemos hablado sobre lo que significa probabilidad y de por qué los estadísticos no se ponen de acuerdo sobre su significado. Hemos hablado de las reglas que deben cumplir las probabilidades. Hemos introducido la idea de distribución de probabilidad y hemos dedicado una buena parte del capítulo a hablar de algunas de las distribuciones de probabilidad más importantes con las que trabajan los estadísticos. El desglose por secciones es el siguiente:
- Teoría de la probabilidad versus estadística: ¿En qué se diferencian la probabilidad y la estadística?
- [La visión frecuentista] versus [La visión bayesiana] de la probabilidad
- Teoría básica de la probabilidad
- La distribución binomial, La distribución normal y Otras distribuciones útiles
Como era de esperar, mi cobertura no es en absoluto exhaustiva. La teoría de la probabilidad es una gran rama de las matemáticas por derecho propio, totalmente independiente de su aplicación a la estadística y el análisis de datos. Como tal, hay miles de libros escritos sobre el tema y las universidades suelen ofrecer múltiples clases dedicadas por completo a la teoría de la probabilidad. Incluso la tarea “más sencilla” de documentar las distribuciones de probabilidad estándar es un gran tema. He descrito cinco distribuciones de probabilidad estándar en este capítulo, pero en mi estantería tengo un libro de 45 capítulos titulado “Distribuciones estadísticas” (Evans et al., 2011) que contiene muchas más. Afortunadamente para ti, muy poco de esto es necesario. Es poco probable que necesites conocer docenas de distribuciones estadísticas cuando salgas a hacer análisis de datos del mundo real, y definitivamente no las necesitarás para este libro, pero nunca está de más saber que hay otras posibilidades por ahí.
Retomando este último punto, hay un sentido en el que todo este capítulo es una especie de digresión. Muchas clases de psicología de grado sobre estadística pasan por alto este contenido muy rápidamente (sé que la mía lo hizo), e incluso las clases más avanzadas a menudo “olvidan” revisar los fundamentos básicos del campo. La mayoría de los psicólogos académicos no conocerían la diferencia entre probabilidad y densidad, y hasta hace poco muy pocos habrían sido conscientes de la diferencia entre probabilidad bayesiana y frecuentista. Sin embargo, creo que es importante comprender estas cosas antes de pasar a las aplicaciones. Por ejemplo, hay muchas reglas sobre lo que está “permitido” decir cuando se hace inferencia estadística y muchas de ellas pueden parecer arbitrarias y extrañas. Sin embargo, empiezan a tener sentido si se entiende que existe esta distinción entre bayesianos y frecuentistas. Del mismo modo, en Chapter 11 vamos a hablar de algo llamado la prueba t, y si realmente quieres comprender la mecánica de la prueba t, te ayudará tener una idea de cómo es realmente una distribución t. Espero que te hagas una idea.
Esto no significa que los frecuentistas no puedan hacer afirmaciones hipotéticas, por supuesto. Lo que ocurre es que si se quiere hacer una afirmación sobre la probabilidad, debe ser posible volver a describir esa afirmación en términos de una secuencia de sucesos potencialmente observables, junto con las frecuencias relativas de los distintos resultados que aparecen dentro de esa secuencia.↩︎
ten en cuenta que el término “éxito” es bastante arbitrario y no implica realmente que el resultado sea algo deseable. Si \(\theta\) se refiriera a la probabilidad de que un pasajero resulte herido en un accidente de autobús, seguiría llamándola probabilidad de éxito, pero eso no significa que quiera que la gente resulte herida en accidentes de autobús.↩︎
Para los lectores que sepan un poco de cálculo, daré una explicación un poco más precisa. Del mismo modo que las probabilidades son números no negativos que deben sumar 1, las densidades de probabilidad son números no negativos que deben integrarse en 1 (donde la integral se toma a lo largo de todos los valores posibles de X). Para calcular la probabilidad de que X se encuentre entre a y b calculamos la integral definida de la función de densidad sobre el intervalo correspondiente, \(\int\_{a}^{b} p(x) dx\). Si no recuerdas o nunca has aprendido cálculo, no te preocupes. No es necesario para este libro.↩︎
En la ecuación de la binomial, \(X!\) es la función factorial (es decir, multiplicar todos los números enteros de 1 a \(X\)): \[P(X | \theta, N) = \displaystyle\frac{N!}{X! (N-X)!} \theta^X (1-\theta)^{N-X}\] Si esta ecuación no tiene mucho sentido para ti, no te preocupes.↩︎
Al igual que en el caso de la distribución binomial, he incluido la fórmula de la distribución normal en este libro, porque creo que es lo suficientemente importante como para que todo el que aprenda estadística deba al menos echarle un vistazo, pero como éste es un texto introductorio no quiereo centrarme en ella, así que la he escondido en esta nota a pie de página: \[p(X|\mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(X-\mu)^2}{2\sigma^2}}\]↩︎
en la práctica, la distribución normal es tan práctica que la gente tiende a utilizarla incluso cuando la variable no es realmente continua. Siempre que haya suficientes categorías (p. ej., las respuestas de una escala Likert a un cuestionario), es una práctica bastante habitual usar la distribución normal como aproximación. Esto funciona mucho mejor de lo que parece.↩︎
Para los lectores que sepan un poco de cálculo, daré una explicación un poco más precisa. De la misma manera que las probabilidades son números no negativos que deben sumar 1, las densidades de probabilidad son números no negativos que deben integrarse a 1 (donde la integral se toma a través de todos los valores posibles de X). Para calcular la probabilidad de que X se encuentre entre a y b calculamos la integral definida de la función de densidad sobre el intervalo correspondiente, \(\int\_{a}^{b} p(x) dx\). Si no recuerdas o nunca has aprendido cálculo, no te preocupes por esto. No es necesario para este libro.↩︎