
5 Dibujando gráficos
Sobre todo mostrar los datos.
– Edward Tufte1
La visualización de datos es una de las tareas más importantes a las que se enfrenta el analista de datos. Es importante por dos razones distintas pero estrechamente relacionadas. En primer lugar, está la cuestión de dibujar “gráficos de presentación”, mostrar tus datos de una manera limpia y visualmente atractiva hace que sea más fácil para el lector entender lo que estás tratando de decirles. Igualmente importante, quizás aún más importante, es el hecho de que dibujar gráficos te ayuda a comprender los datos. Con ese fin, es importante dibujar “gráficos exploratorios” que te ayuden a aprender sobre los datos a medida que los analizas. Estos puntos pueden parecer bastante obvios, pero no puedo contar la cantidad de veces que he visto a la gente olvidarlos.
Para dar una idea de la importancia de este capítulo, quiero comenzar con una ilustración clásica de cuán poderoso puede ser un buen gráfico. Con ese fin, Figure 5.1 muestra un nuevo dibujo de una de las visualizaciones de datos más famosas de todos los tiempos. Este es el mapa de muertes por cólera de John Snow de 1854. El mapa es elegante en su simplicidad. De fondo tenemos un callejero que ayuda a orientar al espectador. En la parte superior vemos una gran cantidad de pequeños puntos, cada uno de los cuales representa la ubicación de un caso de cólera. Los símbolos más grandes muestran la ubicación de las bombas de agua, etiquetadas por su nombre. Incluso la inspección más casual del gráfico deja muy claro que la fuente del brote es casi con certeza la bomba de Broad Street. Al ver este gráfico, el Dr. Snow hizo arreglos para quitar el mango de la bomba y puso fin al brote que había matado a más de 500 personas. Tal es el poder de una buena visualización de datos.
Los objetivos de este capítulo son dos. Primero, discutir varios gráficos bastante estándar que usamos mucho al analizar y presentar datos, y segundo, mostrarte cómo crear estos gráficos en jamovi. Los gráficos en sí tienden a ser bastante sencillos, por lo que, en cierto sentido, este capítulo es bastante simple. Donde la gente suele tener dificultades es en aprender a producir gráficos y, especialmente, aprender a producir buenos gráficos. Afortunadamente, aprender a dibujar gráficos en jamovi es razonablemente simple, siempre y cuando no seas demasiado exigente con el aspecto de tu gráfico. Lo que quiero decir cuando digo esto es que jamovi tiene muchos gráficos predeterminados muy buenos, o tramas, que la mayoría de las veces producen un gráfico limpio y de alta calidad. Sin embargo, si deseas hacer algo no estándar, o si necesitas realizar cambios muy específicos en la figura, la funcionalidad gráfica en jamovi aún no es capaz de admitir trabajos avanzados o edición de detalles.
5.1 Histogramas
Comencemos con el humilde histograma. Los histogramas son una de las formas más sencillas y útiles de visualizar datos. Tienen más sentido cuando tienes una variable de escala de intervalo o razón (p. ej., los datos de afl.margins de Chapter 4 y lo que quieres hacer es obtener una impresión general de la variable. La mayoría probablemente sabéis cómo funcionan los histogramas). Funcionan, ya que se usan mucho, pero para que estén completos, los describiré. Todo lo que debes hacer es dividir los valores posibles en contenedores y luego contar el número de observaciones que caen dentro de cada contenedor. Este conteo se conoce como la frecuencia o densidad del contenedor y se muestra como una barra vertical.En los datos de márgenes ganadores de la AFL, hay 33 juegos en los que el margen ganador fue inferior a 10 puntos y es este hecho el que está representado por la altura de la barra más a la izquierda que mostramos anteriormente en Chapter 4, Figure 4.2. Con los gráficos anteriores, usamos un paquete de trazado avanzado en R que, por ahora, va más allá de la capacidad de jamovi. Pero jamovi nos acerca, y dibujar este histograma en jamovi es bastante sencillo. Abre las opciones de ‘gráficos’ en ‘Exploración’ - ‘Descriptivas’ y haz clic en la casilla de verificación ‘histograma’, como en Figure 5.1. jamovi por defecto etiqueta el eje y como ‘densidad’ y el eje x con el nombre de la variable. Los contenedores se seleccionan automáticamente y no hay información de escala o conteo en el eje y, a diferencia de la Figure 4.2 anterior. Pero esto no importa demasiado porque después de todo lo que realmente nos interesa es nuestra impresión de la forma de la distribución: ¿se distribuye normalmente o hay sesgo o curtosis? Nuestras primeras impresiones de estas características provienen de dibujar un histograma.
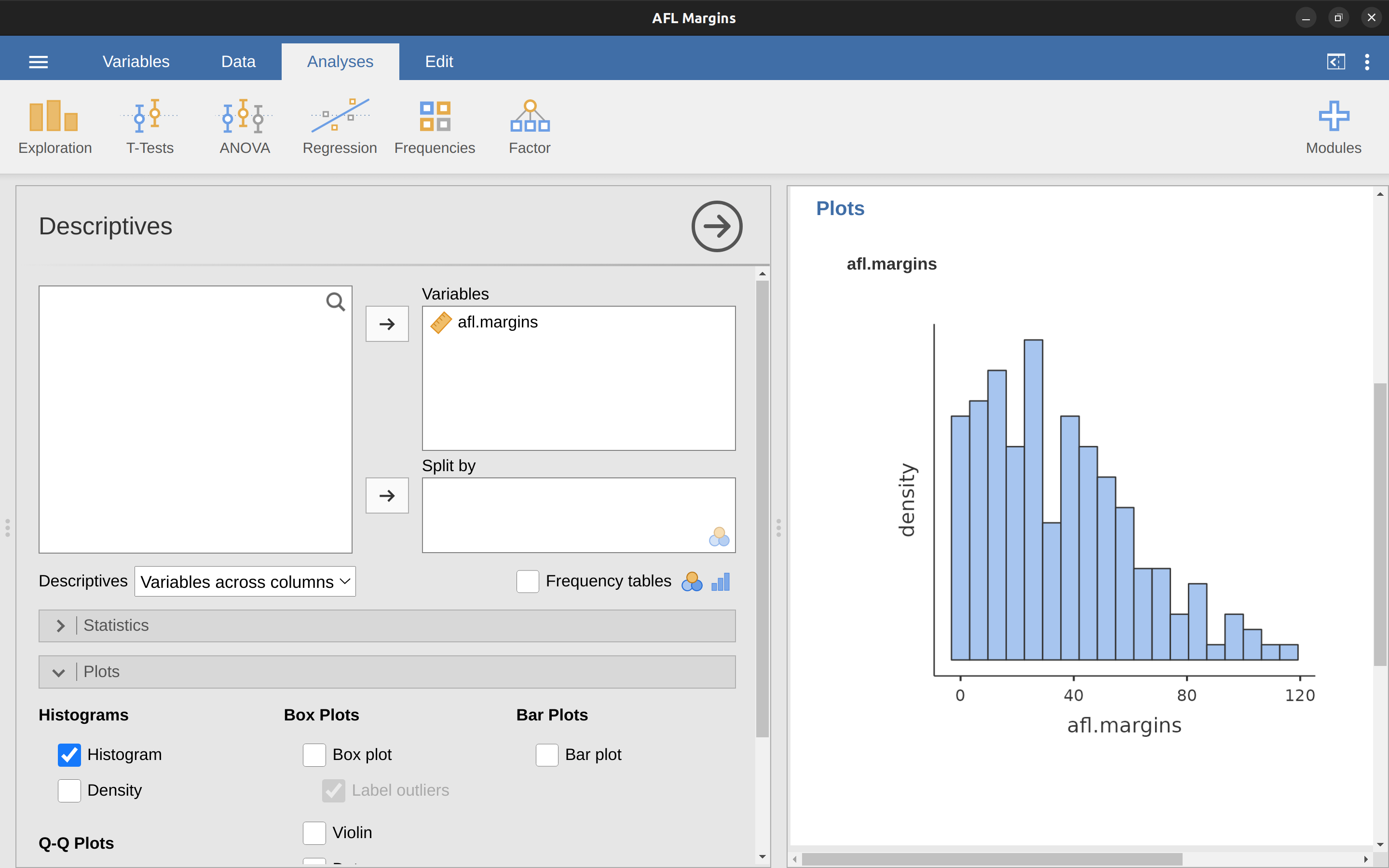
Una característica adicional que proporciona jamovi es la capacidad de trazar una curva de ‘Densidad’. Puedes hacer esto haciendo clic en la casilla de verificación ‘Densidad’ debajo de las opciones de ‘Gráficos’ (y desmarcando ‘Histograma’), y esto nos da el gráfico que se muestra en Figure 5.3. Un gráfico de densidad visualiza la distribución de datos en un intervalo continuo o período de tiempo. Este gráfico es una variación de un histograma que usa suavizado de kernel para trazar valores, lo que permite distribuciones más suaves al suavizar el ruido. Los picos de una gráfica de densidad ayudan a mostrar dónde se concentran los valores en el intervalo. Una ventaja que tienen los gráficos de densidad sobre los histogramas es que son mejores para determinar la forma de distribución porque no se ven afectados por la cantidad de contenedores utilizados (cada barra utilizada en un histograma típico). Un histograma compuesto por solo 4 contenedores no produciría una forma de distribución lo suficientemente distinguible como lo haría un histograma de 20 contenedores. Sin embargo, con gráficos de densidad, esto no es un problema.
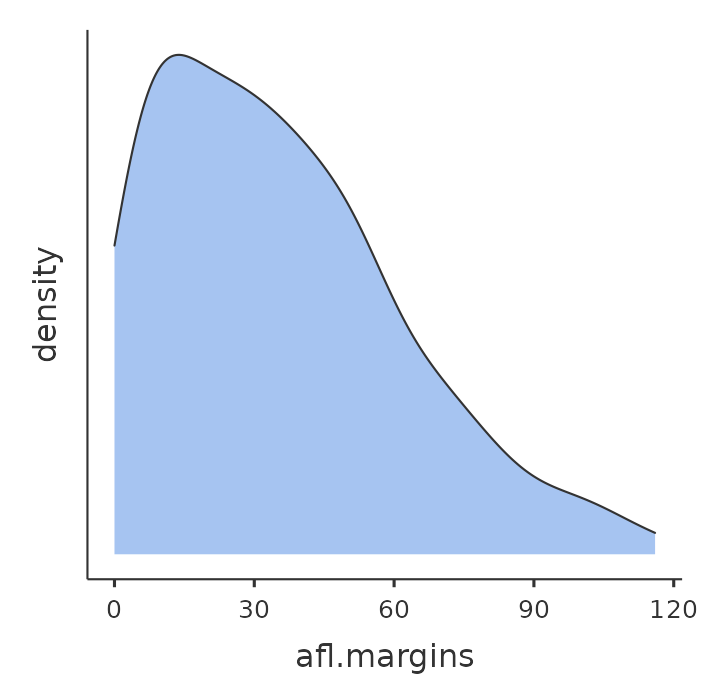
Aunque esta imagen necesitaría mucha limpieza para hacer un buen gráfico de presentación (es decir, uno que incluirías en un informe), hace un buen trabajo al describir los datos. De hecho, la gran fortaleza de un histograma o gráfico de densidad es que (utilizado correctamente) muestra la distribución completa de los datos, por lo que puedes tener una idea bastante clara de cómo se ve. La desventaja de los histogramas es que no son muy compactos. A diferencia de algunas de las otras tramas de las que hablaré, es difícil meter 20-30 histogramas en una sola imagen sin abrumar al espectador. Y, por supuesto, si tus datos son de escala nominal, los histogramas son inútiles.
5.2 Diagramas de caja
Otra alternativa a los histogramas es un diagrama de caja, a veces llamado diagrama de “caja y bigotes”. Al igual que los histogramas, son más adecuados para datos de escala de razón o de intervalo. La idea que subyace a un diagrama de caja es proporcionar una representación visual simple de la mediana, el rango intercuartílico y el rango de los datos. Y debido a que lo hacen de una manera bastante compacta, los diagramas de caja se han convertido en un gráfico estadístico muy popular, especialmente durante la etapa exploratoria del análisis de datos cuando intentas comprender los datos tú misma. Echemos un vistazo a cómo funcionan, usando nuevamente los datos de afl.margins como ejemplo.

La forma más sencilla de describir un diagrama de caja es dibujar uno. Haz clic en la casilla de verificación ‘Diagrama de caja’ y obtendrás el gráfico que se muestra en la parte inferior derecha de Figure 5.4. jamovi ha dibujado el diagrama de caja más básico posible. Así es como debe interpretarse este gráfico: la línea gruesa en el medio del cuadro es la mediana; el cuadro en sí abarca el rango del percentil 25 al percentil 75; y los “bigotes” salen al punto de datos más extremo que no excede un cierto límite. De forma predeterminada, este valor es 1,5 veces el rango intercuartílico (RIC), calculado como el percentil 25 - (1,5*IQR) para el límite inferior y el percentil 75 + (1,5*IQR) para el límite superior. Cualquier observación cuyo valor se encuentre fuera de este rango se traza como un círculo o un punto en lugar de estar cubierto por los bigotes, y normalmente se lo denomina valor atípico. En nuestros datos de márgenes AFL hay dos observaciones que caen fuera de este rango, y estas observaciones se trazan como puntos (el límite superior es 107, y mirando la columna de datos en la hoja de cálculo hay dos observaciones con valores más altos que este, 108 y 116, así que estos son los puntos).
5.2.1 Diagramas de violín
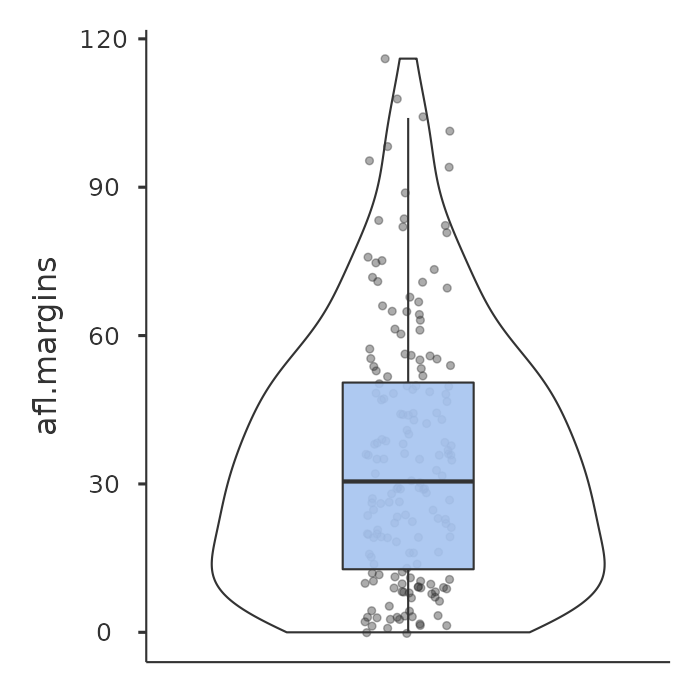
Una variación del diagrama de caja tradicional es el diagrama de violín. Los diagramas de violín son similares a los diagramas de caja, excepto que también muestran la densidad de probabilidad de kernel de los datos en diferentes valores. Por lo general, los diagramas de violín incluirán un marcador para la mediana de los datos y un cuadro que indica el rango intercuartílico, como en los diagramas de caja estándar. En jamovi, puedes conseguir este tipo de funcionalidad marcando las casillas de verificación ‘Violín’ y ‘Box plot’. Consulta Figure 5.5, que también tiene activada la casilla de verificación ‘Datos’ para mostrar los puntos de datos reales en el gráfico. Sin embargo, esto hace que el gráfico esté demasiado recargado, en mi opinión. La claridad es simplicidad, por lo que en la práctica sería mejor usar un simple diagrama de caja.
5.2.2 Dibujar múltiples diagramas de caja
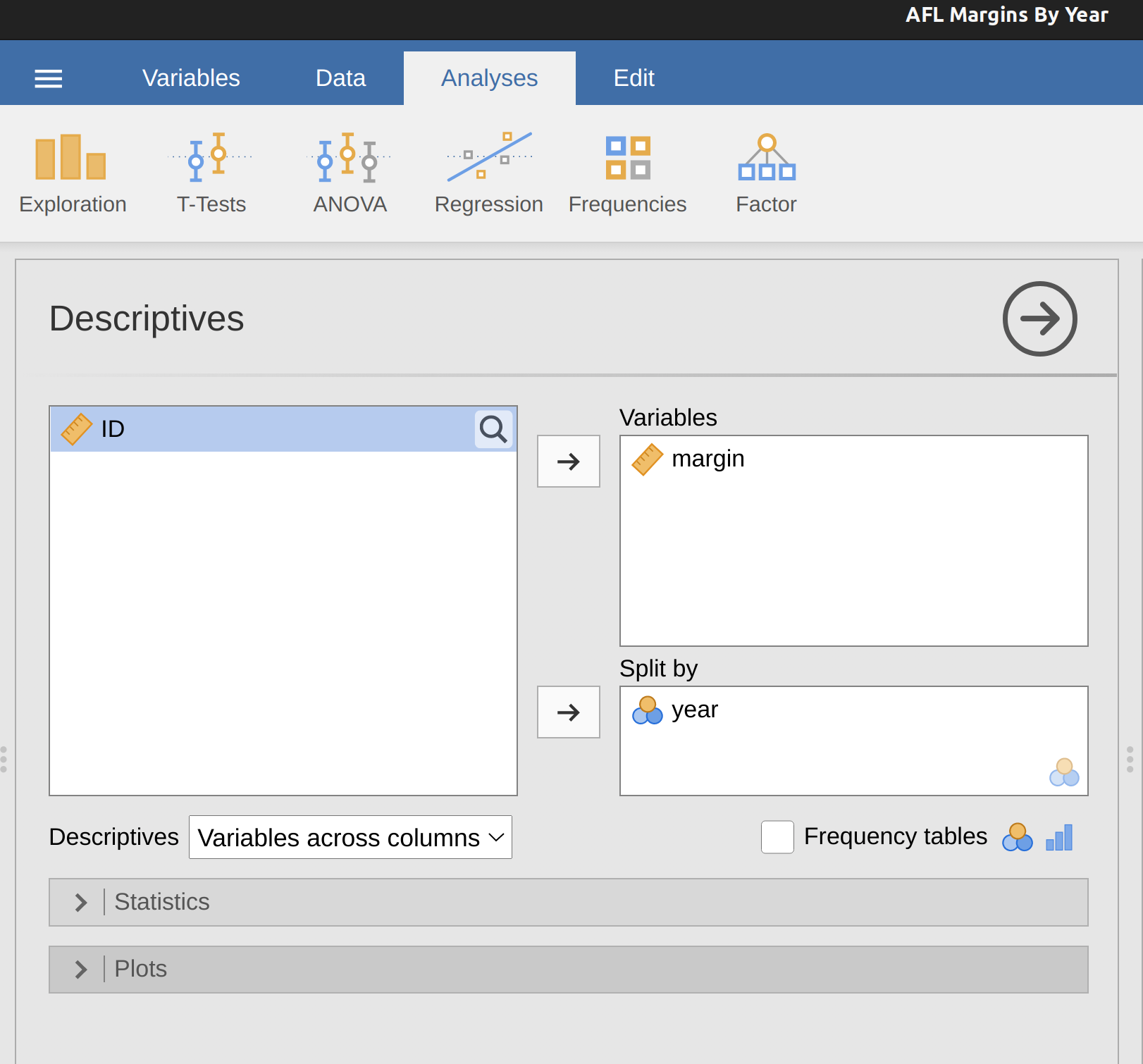
Una última cosa. ¿Qué sucede si quieres dibujar varios diagramas de caja a la vez? Supongamos, por ejemplo, que quisieras diagramas de caja separados que mostraran los márgenes de AFL no solo para 2010 sino para todos los años entre 1987 y 2010. Para hacer eso, lo primero que tendremos que hacer es encontrar los datos. Estos se almacenan en el archivo aflmarginbyyear.csv. Carguémoslo en jamovi y veamos qué contiene. Verás que es un conjunto de datos bastante grande. Contiene 4296 juegos y las variables que nos interesan. Lo que queremos hacer es que jamovi dibuje diagramas de caja para la variable de margen, pero graficados por separado para cada año. Para hacer esto tienes que mover la variable del año al cuadro ‘Dividir por’, como en Figure 5.6.
El resultado se muestra en Figure 5.7. Esta versión del diagrama de caja, dividida por año, da una idea de por qué a veces es útil elegir diagramas de caja en lugar de histogramas. Es posible tener una buena idea del aspecto de los datos de un año a otro sin abrumarse con demasiados detalles. Imagina lo que hubiera pasado si hubieras intentado meter 24 histogramas en este espacio: no hay ninguna posibilidad de que el lector aprenda nada útil.

5.2.3 Uso de diagramas de caja para detectar valores atípicos
Dado que el diagrama de caja separa automáticamente aquellas observaciones que se encuentran fuera de un cierto rango, representándolas con un punto en jamovi, la gente a menudo los usa como un método informal para detectar valores atípicos: observaciones que están “sospechosamente” distantes del resto de los datos. Aquí hay un ejemplo. Supongamos que dibujé el diagrama de caja para los datos de márgenes de AFL y apareció como Figure 5.8. Está bastante claro que algo raro ocurre con dos de las observaciones. ¡Aparentemente, hubo dos juegos en los que el margen superó los 300 puntos! Eso no me suena bien. Ahora que he comenzado a sospechar, es hora de mirar un poco más de cerca los datos. En jamovi, puedes averiguar rápidamente cuáles de estas observaciones son sospechosas y luego puedes volver a los datos sin procesar para ver si ha habido un error en la entrada de datos. Una forma de hacer esto es decirle a jamovi que etiquete los valores atípicos, marcando la casilla junto a la casilla de verificación Diagrama de caja. Esto agrega una etiqueta de número de fila al lado del valor atípico en el diagrama de caja, para que puedas mirar esa fila y encontrar el valor extremo. Otra forma, más flexible, es configurar un filtro para que solo se incluyan aquellas observaciones con valores por encima de un cierto umbral. En nuestro ejemplo, el umbral es superior a 300, por lo que ese es el filtro que crearemos. Primero, haz clic en el botón ‘Filtros’ en la parte superior de la ventana jamovi y luego escribe ‘margen > 300’ en el campo de filtro, como en Figure 5.9.

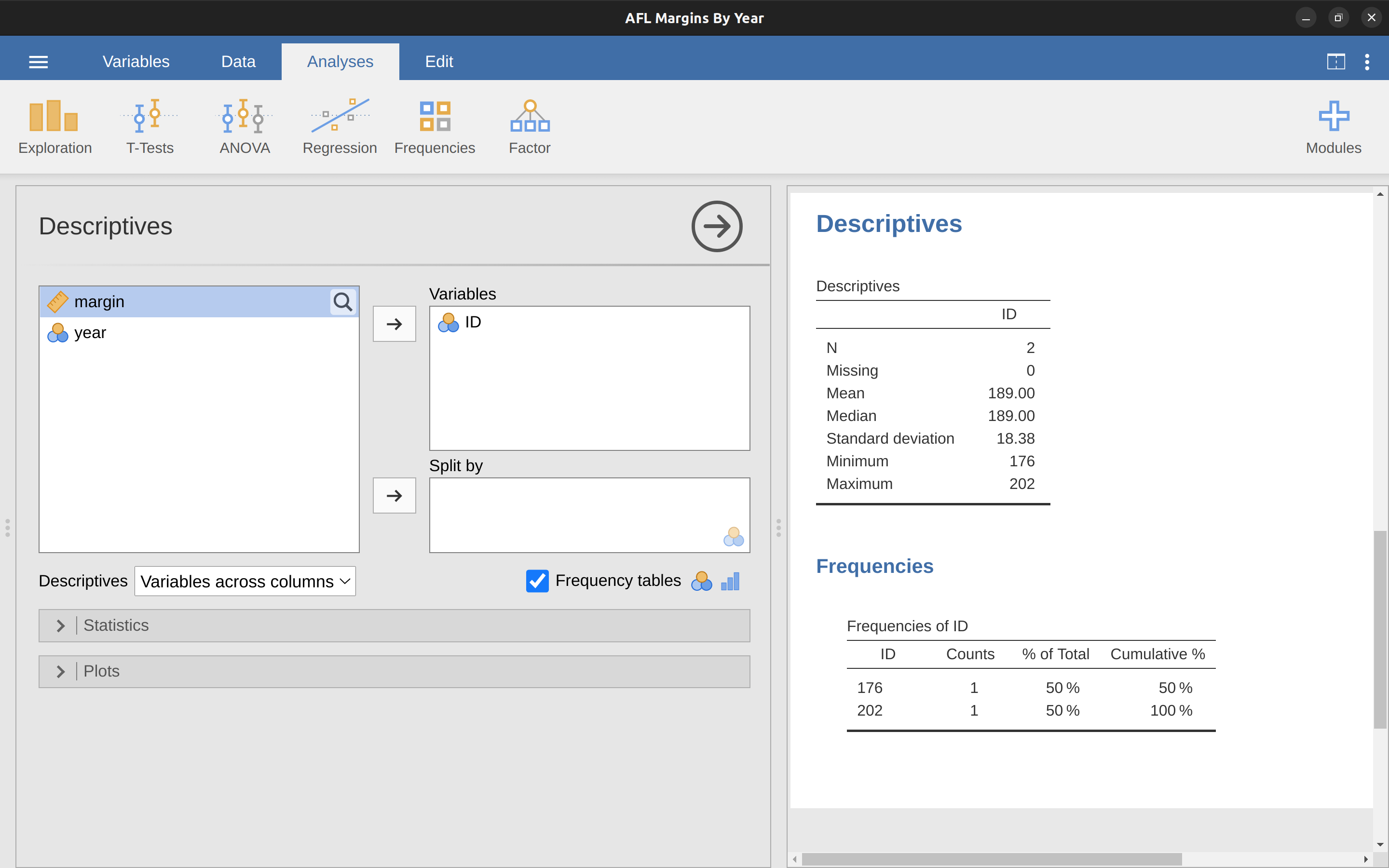
Este filtro crea una nueva columna en la vista de hoja de cálculo donde solo se incluyen aquellas observaciones que pasan el filtro. Una buena manera de identificar rápidamente qué observaciones son estas es decirle a jamovi que produzca una ‘Tabla de frecuencia’ (en la ventana ‘Exploración’ - ‘Descriptivas’) para la variable ID (que debe ser una variable nominal; de lo contrario, la tabla de frecuencia no se genera). En Figure 5.10 puedes ver que los valores de ID para las observaciones donde el margen era superior a 300 son 14 y 134. Estos son casos u observaciones sospechosas, donde debes volver a la fuente de datos original para averiguar qué está pasando.

Suele ocurrir que alguien se equivoca de número. Aunque esto pueda parecer un ejemplo tonto, debo subrayar que este tipo de cosas ocurren realmente a menudo. Los conjuntos de datos del mundo real suelen estar plagados de errores estúpidos, especialmente cuando alguien ha tenido que teclear algo en un ordenador en algún momento. De hecho, esta fase en el análisis de datos tiene un nombre y, en la práctica, puede ocupar una gran parte de nuestro tiempo: limpieza de datos. Consiste en buscar errores tipográficos (“erratas”), datos faltantes y todo tipo de errores molestos en los archivos de datos brutos.
En el caso de los valores menos extremos, incluso si se marcan en un gráfico de caja como valores atípicos, la decisión de incluirlos o excluirlos en cualquier análisis depende en gran medida de por qué crees que los datos son como son y para qué quieres utilizarlos. En este caso hay que actuar con buen criterio. Si el valor atípico te parece legítimo, consérvalo. En cualquier caso, volveré al tema nuevamente en Section 12.10 en Chapter 12.
5.3 Gráficos de barras
Otra forma de gráfico que a menudo se desea trazar es el gráfico de barras. Utilicemos el conjunto de datos afl.finalists con la variable afl.finalists que introduje en Section 4.1.6. Lo que quiero hacer es dibujar un gráfico de barras que muestre la cantidad de finales en las que ha jugado cada equipo durante el tiempo que abarca el conjunto de datos afl.finalists. Hay muchos equipos, pero estoy particularmente interesada en solo cuatro: Brisbane, Carlton, Fremantle y Richmond. Así que el primer paso es configurar un filtro para que solo esos cuatro equipos se incluyan en el gráfico de barras. Esto es sencillo en jamovi y puedes hacerlo usando la función ‘Filtros’ que usamos anteriormente. Abre la pantalla ‘Filtros’ y escribe lo siguiente:
afl.finalistas \(==\) ‘Brisbane’ o afl.finalistas \(==\) ‘Carlton’ o afl.finalistas \(==\) ‘Fremantle’ o afl.finalistas \(==\) ‘Richmond’ 2
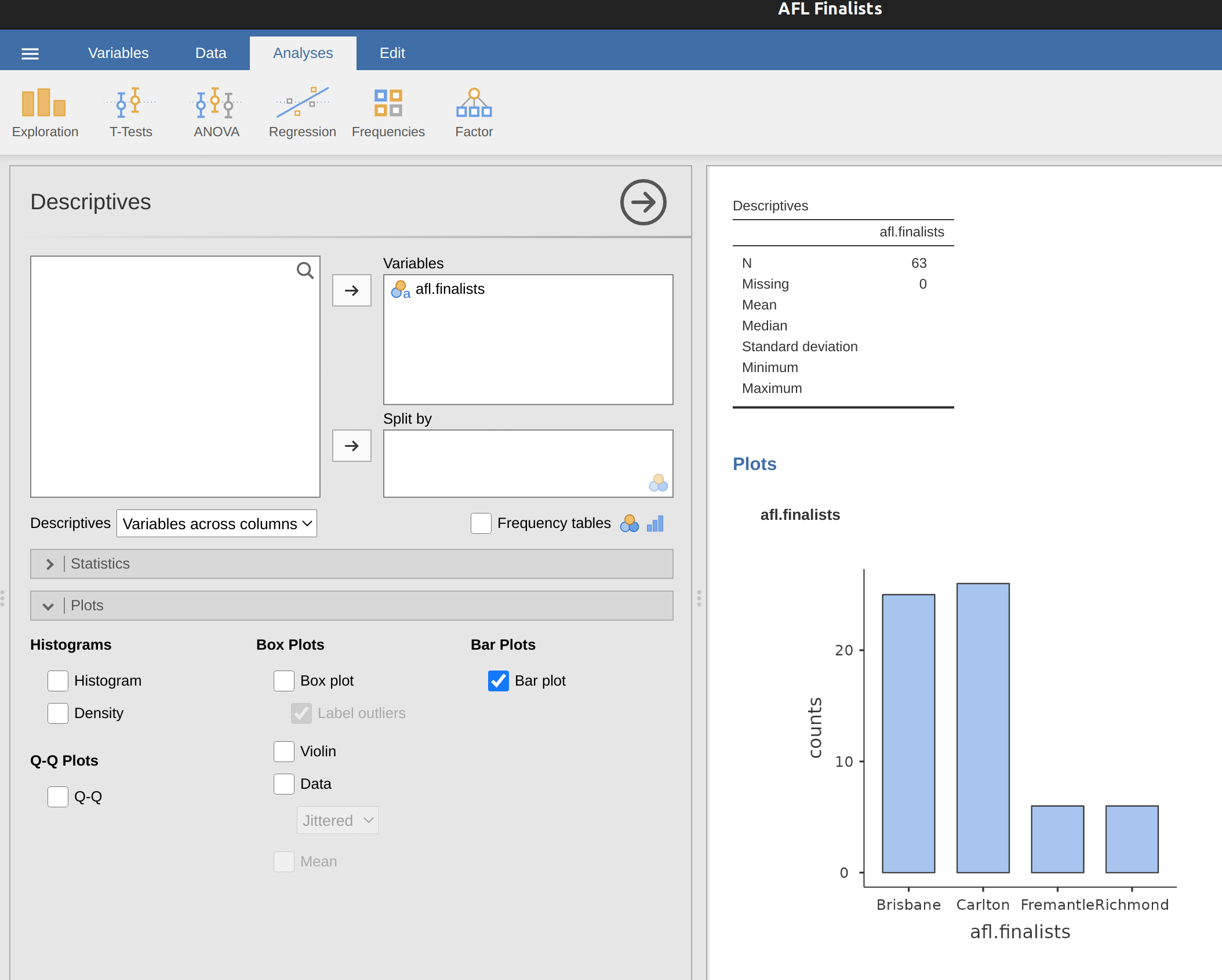
Cuando hayas hecho esto, verás, en la vista ‘Datos’, que jamovi ha filtrado todos los valores excepto los que hemos especificado. A continuación, abre la ventana ‘Exploración’ - ‘Descriptivas’ y haz clic en la casilla de verificación ‘Gráfico de barras’ (recuerda mover la variable ‘afl.finalists’ al cuadro ‘Variables’ para que jamovi sepa qué variable usar). Luego deberías obtener un gráfico de barras, algo como el que se muestra en Figure 5.11.
5.4 Guardar archivos de imagen usando jamovi
Espera, estarás pensando. ¿De qué sirve poder hacer dibujos bonitos en jamovi si no puedo guardarlos y enviárselos a mis amigos para alardear de lo increíbles que son mis datos? ¿Cómo guardo la imagen? Muy sencillo. Haz clic con el botón derecho del ratón en la imagen del gráfico y expórtala a un archivo, ya sea como ‘png’, ‘eps’, ‘svg’ o ‘pdf’. Todos estos formatos producen bonitas imágenes que luego puedes enviar o incluir en tus tareas o trabajos.
5.5 Resumen
Tal vez soy una persona de mente simple, pero me encantan las fotos. Cada vez que escribo un nuevo artículo científico, una de las primeras cosas que hago es sentarme y pensar en cuáles serán las imágenes. En mi cabeza, un artículo no es más que una secuencia de imágenes unidas por una historia. Todo lo demás es solo un escaparate. Lo que realmente estoy tratando de decir aquí es que el sistema visual humano es una herramienta de análisis de datos muy poderosa. Dale el tipo correcto de información y proporcionará al lector humano una gran cantidad de conocimiento muy rápidamente. No en vano tenemos el dicho “una imagen vale más que mil palabras”. Con eso en mente, creo que este es uno de los capítulos más importantes del libro. Los temas tratados fueron:
- Gráficos comunes. Gran parte del capítulo se centró en los gráficos estándar que a los estadísticos les gusta producir: Histogramas, Diagramas de caja y Gráficos de barras
- Guardar archivos de imagen usando jamovi. Es importante destacar que también cubrimos cómo exportar sus imágenes.
Una última cosa a señalar. Si bien jamovi produce algunos gráficos predeterminados realmente buenos, actualmente no es posible editarlos. Para gráficos más avanzados y capacidad de trazado, los paquetes disponibles en R son mucho más potentes. Uno de los sistemas de gráficos más populares lo proporciona el paquete ggplot2 (ver https://ggplot2.tidyverse.org/), que se basa libremente en “La gramática de los gráficos” (Wilkinson et al., 2006). No es para novatos. Necesitas tener un conocimiento bastante bueno de R antes de poder comenzar a usarlo, e incluso entonces lleva un tiempo dominarlo. Pero cuando esté listo, vale la pena tomarse el tiempo para aprender por ti misma, porque es un sistema mucho más poderoso y más limpio.